基于潜在状态变量的多结构突变同时检测方法
王小刚
(北方民族大学 数学与信息科学学院,银川 750021)
0 引言
结构突变的识别、估计和检验一直是统计学和计量经济学中的热点问题之一,许多学者对该问题进行了广泛而深入的研究。随着经济、金融、生物等领域中面板数据的频繁使用,在面板数据模型中深入研究结构突变理论就成为统计学家重要的研究方向之一[1,2]。在面板数据中研究结构突变理论,不仅给研究者和政策制定者理解突变点的实际意义提供了理论保证和指导作用,而且为有针对性地提出和制定政策提供了重要的参考价值,对防范崩溃式的突变有重要的风险警示意义。
目前,在存在多个结构突变的检测中,通常采用的办法是序贯检测方法,即先假定只存在一个突变点进行检测,然后利用已估计的突变点将数据分为两段(突变前数据和突变后数据),再利用前述方法进行检测,直至检测不出突变点为止。序贯检测方法易于理解、操作性强,缺点在于不能满足同时检测情形,不利于实时监测突变。在实际应用中,经常会考虑突发事件(如金融危机、财政货币政策变化、技术变革等)对社会、经济、金融领域的影响,此时如何正确管理风险取决于人们能否快速的检测到发生突发事件的时间和影响程度。此时,人们可能更加关心同时检测出多个影响时刻而不是序贯检测多个时刻。
多个结构突变的同时检测方法主要基于贝叶斯方法,通过将突变参数的估计转化为对潜在状态变量的估计来解决。Chib[3]提出了不可逆的隐马尔可夫链方法对多突变进行估计,通过对状态变量的检测来检测突变点的个数和位置,这种方法对描述复杂的突变点非常有效,Pesaran等[4]将其应用于检测时间序列数据中的多个突变。该方法通常得到的后验分布需通过MCMC递归抽样得到,即先在样本和其他参数已知的条件下对状态进行抽样,然后在样本和状态已知的条件下对参数和转移矩阵抽样[3,5]。通过定义潜在状态变量估计多个突变点的方法有三个方面的优点:一是状态个数的确定不依赖于样本也不取决于未来值;二是状态之间可以提供更多关于共同分布的信息;三是该方法计算量小,可靠性强。但是,该方法的缺陷在于过于繁琐,Geweke和Jiang[6]通过用一个Bernoulli潜变量st表示状态改变的做法简化了上述方法,假设时间序列数据存在多个突变点,令观测值服从均值和方差存在突变点的正态分布,对均值参数、方差参数以及状态变量引入先验分布,利用分层贝叶斯方法解决对状态变量的估计,从而得到多个突变点的估计,但是Geweke和Jiang[6]的方法并不能适用于面板数据。本文基于潜在状态变量对存在的多个结构突变的面板模型进行同时检测,利用贝叶斯方法和不可逆隐马尔可夫链检测面板数据中存在的多个突变,得到突变点的个数和位置估计,并将该方法应用到2003—2014年中国五省市的通货膨胀数据的检测中,发现存在四个突变点,并对每个突变点产生的原因做了分析。
1 不可逆隐马尔可夫链方法
假设时间序列数据{yt}(t=1,2,…,T)在时间区间[1,T]上存在着M个突变(即M+1个状态),突变表示为{km}(m=1,2,…,M),当突变点的个数大于1时,联合密度为f(k1,k2,…,kM),即:

在估计参数时,需要给出[1,T]上每一突变点km可能的取值,即:
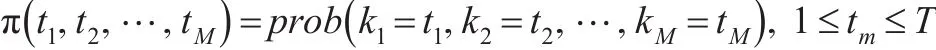
令 ST=(s1,s2,…,sT),其中每一个分量 st都是表示状态离散的潜变量,取值集合为{1,2,…,M+1}(假设t=1时刻时状态为1,则最后一个状态为M+1),且有 s1<s2<…<sT。序列{st}为马尔可夫链,记其转移矩阵为P:
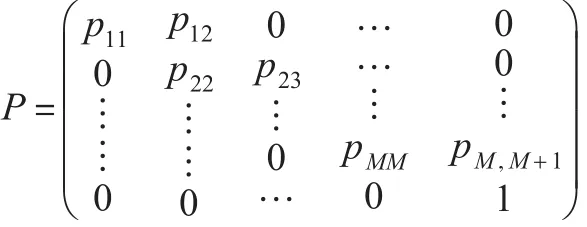
其中 pij=prob(st=j|st-1=i)是给定t-1时刻状态为i的条件下t时刻跳转到状态j的概率,且pii+pi,i+1=1。尽管该方法并未直接给出km的估计值,但可以通过计算每段{t:st=m}的长度而得到km的估计。每个突变点发生的时刻即为st值向前跳转一步的时刻:
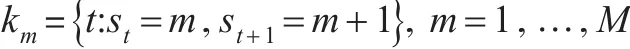
该方法将原本每个个体需要估计TM次的复杂步骤简化为每个个体只需估计M个参数{pmm}即可,所以能大大提高计算效率。突变点的概率可以表示为:

其中t0=0。若已知的待估参数θ和转移矩阵P的先验分布,可以利用贝叶斯公式得到参数的后验密度:

Geweke和Jiang[6]通过用一个Bernoulli潜变量st表示状态改变的做法简化了上述方法,假设时间序列数据yt存在多个突变,假设发生突变的概率是相同的,用 prob表示,若st=0表示t和t+1时刻在同一状态里,st=1表示t和t+1时刻不在同一状态。在每个状态jt时,假设观测值服从均值和方差存在突变的正态分布,即:

然后对均值参数、方差参数以及状态变量引入先验分布,利用分层贝叶斯方法解决对状态变量的估计,从而得到突变的估计。
2 基于潜在状态变量的多结构突变检测方法
2.1 模型介绍
本文将在静态面板模型中引入潜在的状态来描述突变,通过对状态的识别得到突变估计。假设状态之间的改变用Bernoulli潜变量st表示,prob(st=1)=π。令:
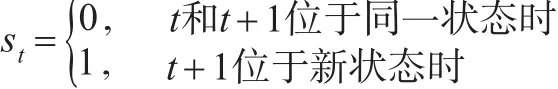
对于面板数据 yit,i=1,2,…,N,t=1,2,…,T ,在每一个状态 jt下(在不引起混淆的情况下简写为状态 j),考虑最简单的情形:

其中 εit~iid N(0,h-1ij),假设参数向量 (μij,hij)服从正态伽玛分布,即:

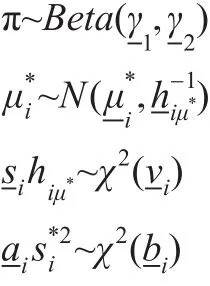
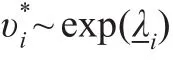
2.2 突变估计的贝叶斯方法
因为 s=(s1,s2,…,sT-1)'是一个含参数 π 的Bernoulli过程,密度为:
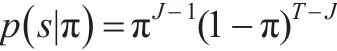
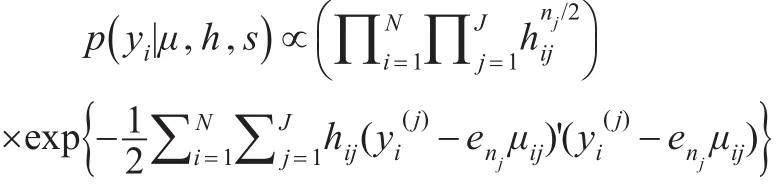
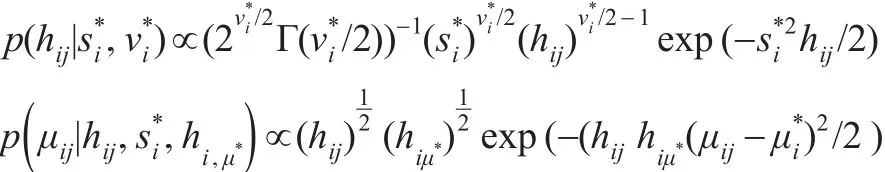
其他参数的先验密度为:
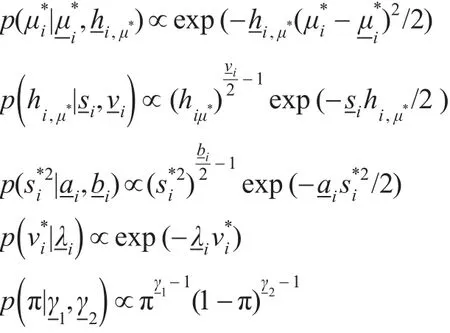
对于个体i和 j=1,2,…,J,相应的后验密度为:
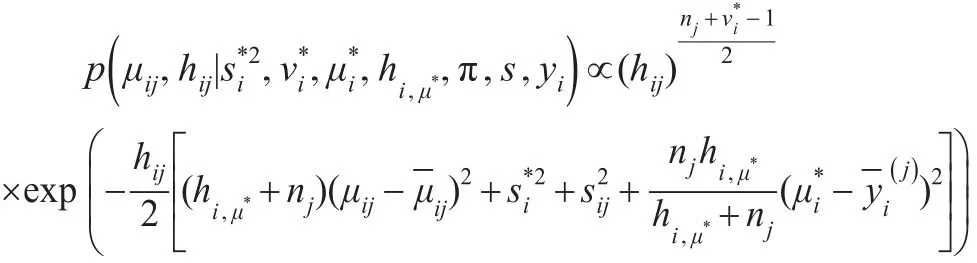
其中:
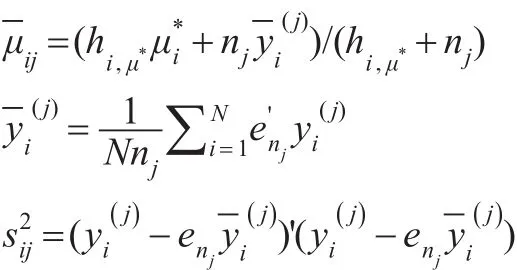
因为随机向量(μij,hij)是条件独立的,并且对于每个个体i服从正态伽玛分布,故:
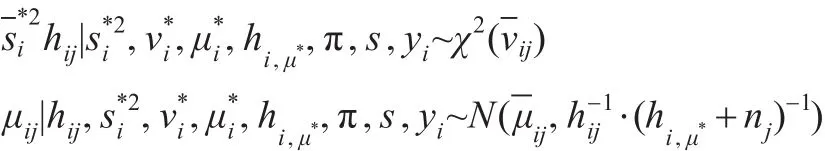
其中:
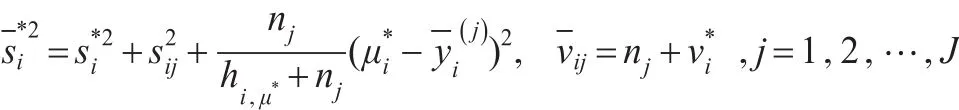
从上述参数分布中可以得到参数的边际后验密度:
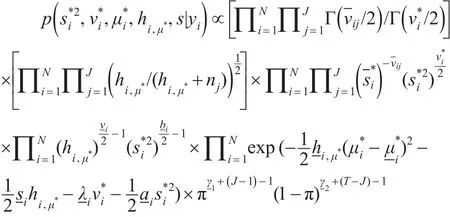
将上式中其他参数积分掉,即可得到其他参数的边际后验密度:
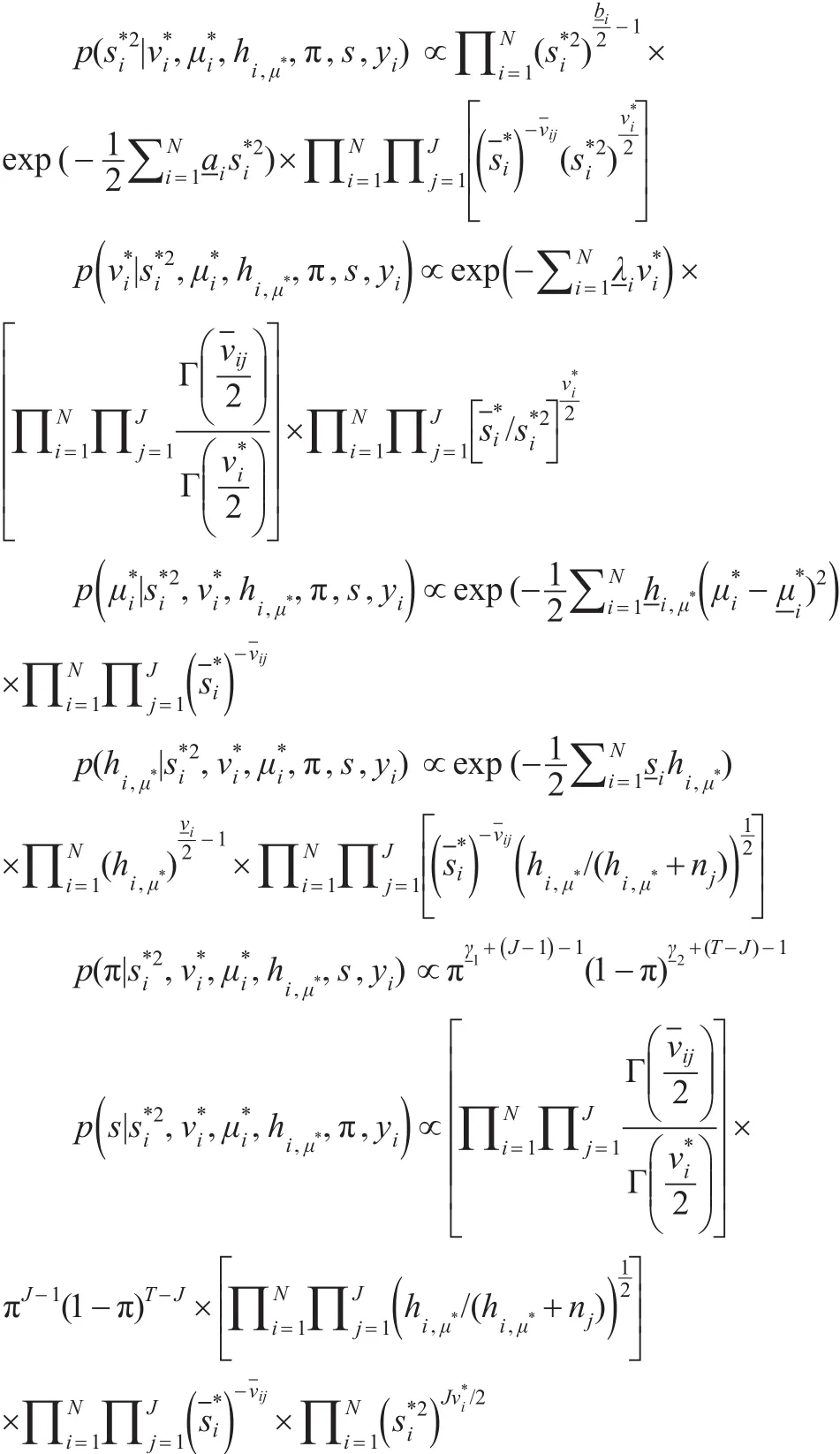
3 五省市CPI通胀率突变的贝叶斯分析
居民消费价格指数(CPI)反映的是在一定时期内居民所消费商品和服务项目的价格水平变动趋势和程度,居民消费价格水平的变动率在一定程度上反映了通货膨胀(或通货紧缩,简称通胀或通缩)的程度,在研究中常用CPI通胀率作为衡量通胀水平的一个数指标[7]。一般认为CPI增长率在3%以内属于温和通胀,而超过5%则属于严重通胀。而通货膨胀作为货币政策分析的重要变量,不仅是国家宏观经济政策调控的参考指标,而且关系到经济发展和社会稳定。它既是全球央行制订货币政策的重要指标,也是中国人民银行构建和完善货币政策传导机制的核心要素。
目前,在研究通胀率的文献中,常采用的通胀率指标有CPI通胀率、商品零售价格指数通胀率(RPI)、GDP平减指数通胀率和核心CPI通胀率等,基于不同指数计算的通胀率侧重点不同[8]。其中,由于CPI数据的可获得性高和分析中的频繁采用,所以在分析中常通过对CPI数据计算而得的CPI通胀率来研究通胀问题。
然而,通胀过程在货币政策和经济环境的作用下不是一成不变的,当遭受重大冲击后可能会使得模型结构发生某种变化,也会导致各省市通货膨胀的动态过程发生突变,而度量这种变化的重要方法之一是在模型中引入结构突变,但现有的文献较少对通胀过程存在的突变进行研究。事实上,我国是一个经济发展很不平衡的国家,这种不平衡导致我国各省市通胀过程存在着显著差异,因而有必要对各省市通胀过程存在的突变进行研究。与宏观政策和货币政策的结构变化相吻合,中国的通胀率自20世纪90年代以来经历了冲高回低的显著变化。然而已有的文献中基于突变对通胀问题进行深入研究的却相对较少,张成思和刘志刚[9]基于中国CPI通胀率的研究发现我国通胀水平一直处于高位运行,1996年末发生了突变,此后通胀水平虽有所下降,但仍保持较高水平。下面将利用已给出的面板数据均值方差发生多个突变的贝叶斯方法对我国五省市CPI通胀率的动态过程进行研究,并从研究结果中分析CPI通胀率发生突变的原因。
3.1 五省市CPI通胀率的描述性分析
为了更直观地反映通货膨胀的动态过程,本文选取北京、上海、江苏、浙江和广东这五个中国经济最发达的省市2003—2014年的CPI通胀率月度数据为样本进行研究,数据来源于中经网统计数据库。虽然目前的学术界将2000年作为我国新一轮经济周期的开始,但是2000年和2001年的CPI都低于1%,2002年还出现了物价下跌和通货紧缩现象,故本文选取2003年作为研究CPI通胀率的起始点,为了避免类似春节等重要的节假日因素对通胀率的影响,将月度数据转化为季度数据。首先将五省市2003年1月到2014年12月的CPI月度环比数据转化为以2003年1月为基期的定基数据,在此基础上得到季度CPI数据,以季度数据的增长率为CPI通胀率数据(下文简称通胀率)。
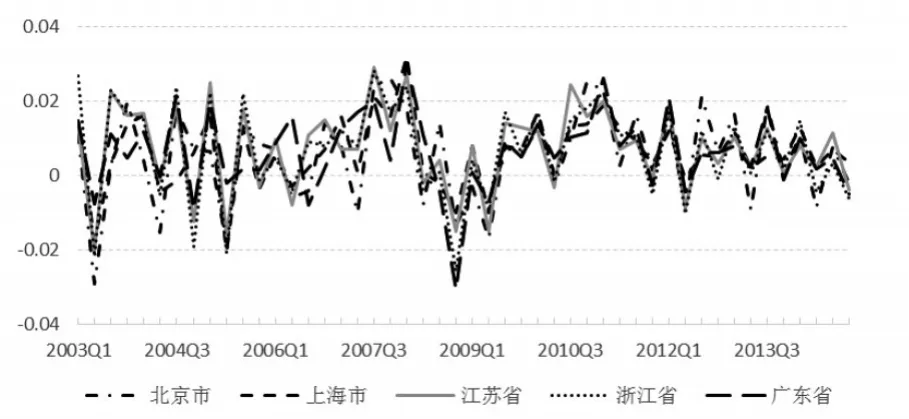
图1 中国五省市2003Q1—2014Q4的通胀率
图1给出了2003年1季度到2014年4季度五省市通胀动态过程的折线图,以反映我国五省市通胀的规律和特点。整体来看,这五省市的通胀是温和的,不确定性和波动性在逐渐减小。从图1中可以看出,五省市通胀率的动态走势相似,皆围绕着横轴上下波动,波动范围为-4%~4%。而2003年1季度到2006年3季度之间五省市通胀率的波动幅度较大,但在2006年4季度到2007年4季度间波动减小,呈现通胀趋势,2008年1季度到2011年2季度之间波动幅度最大,呈现先通胀后通缩趋势,2011年3季度之后波动性减小,呈现通货紧缩趋势。五省市通货膨胀的动态过程大体相似,通胀率的描述性统计量由表1给出。

表1 2003Q1—2014Q4五省市通胀率的统计特征
由表1可知,五省市通胀率的均值和标准差之间的差异几乎不显著,这意味着五省份通胀率可能有相似的结构,有利于本文使用结构突变模型对五省市的通胀率进行分析。而基于不同省市标准差和均值综合考虑的变异系数来看,五省市通胀率的变异系数存在差异,北京的通胀率变异程度最高,其次是浙江、广东和江苏,最后是上海。那么这些表面上的差异是否会对五省市的通货膨胀动态过程产生不同的特征呢?接下来,本文将利用面板数据模型拟合这五省市的通胀率,并尝试基于该模型研究五省市通货率的突变点,以此划分通胀率的变化特征。
3.2 五省市通胀动态过程结构突变的贝叶斯分析
对于北京、上海、江苏、浙江和广东五省市的通胀率数据 πit,i=1,2,…,5,t=1,2,…,48,在每一个状态 jt下,假设:
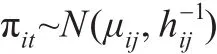
参数向量(μij,hij)的先验分布假设为正态伽玛分布,即:
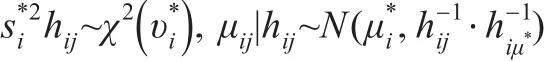
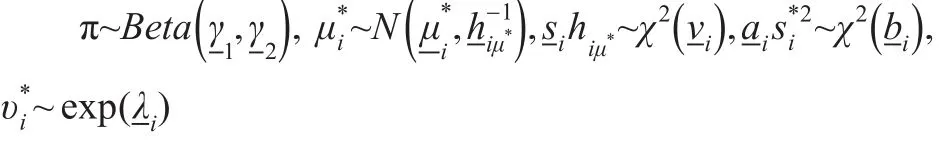
步骤1:用样本均值表示 yi=(yi1,yi2,…,yiN)'的无条件均值,即:


步骤4:hiμ*的均值可以利用 yi方差的4倍与五省市年通胀率的方差之比得到,其中年通胀率用每年各季度通胀率的平均值替代,故:
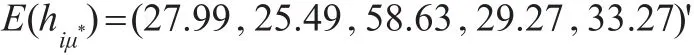
取 -νi=8 ,则 -si=8/E(hiμ*)。
步骤5:π的识别是利用季度数据可能的最大突变个数与样本中可能的突变的个数之比得到(T-1=47),即令
步骤6:除指数分布的参数外,其他先验参数的标准差取为相应均值的一半。
先验参数的选取见表2。
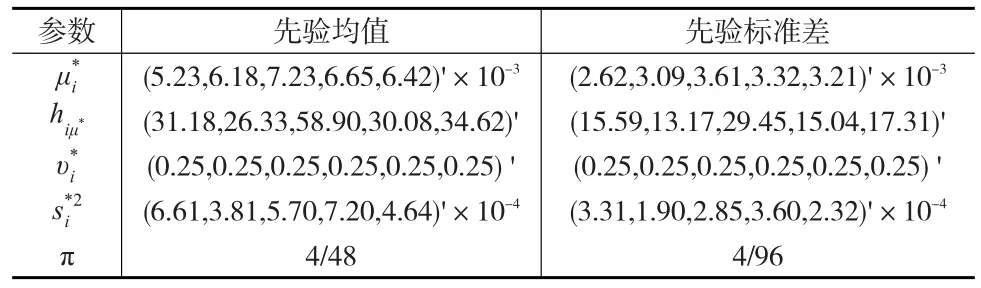
表2 先验参数的选取
3.3 结构突变估计
基于模型和表2中对参数先验分布的选取,对五省市的通胀率进行拟合,并估计了通胀率突变个数和位置。为了保证贝叶斯估计结果的收敛性,本文选取了三组不同的初始值生成三条马尔可夫链,每条马尔可夫链的迭代次数为110000次。为了避免初始值的影响本文去除前10000次burn-in样本,最后得到包含1000次抽样的后验样本。估计结果见图2和表3。
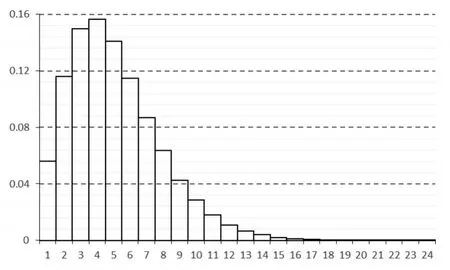
图2 状态变量个数后验分布的直方图
图2给出了状态变量个数后验分布的直方图,其后验均值为4.09,后验标准差为2.76,后验中位数为4,置信水平为95%的后验区间为[2,11]。表3给出了五省市通胀率突变的分层贝叶斯估计中后验概率最大的七个时间点,这七个时间点就是通胀率最有可能发生变化的位置。从图2中可以看出,当状态变量的取值为4时后验分布的概率最大。由此本文认为五省市在样本期2003年1季度到2014年4季度间最有可能存在4个状态,即3个突变点,突变点的可能位置可由表3得出。

表3 具有高后验概率的结构突变估计
由表3可得,其中2006年第4季度、2008年第1季度、2013年第3季度的后验概率最大,其中2007年第3季度和2008年第1季度相距很近,本文认为只有2006年第4季度、2008年第1季度和2013年第3季度是检测出的突变点时刻,这与状态变量的估计结果和对图1的分析基本吻合。
本文以上述四个突变时刻作为界限将样本分为五个状态,分析四次突变前后五省市通胀率的变化,见表4。
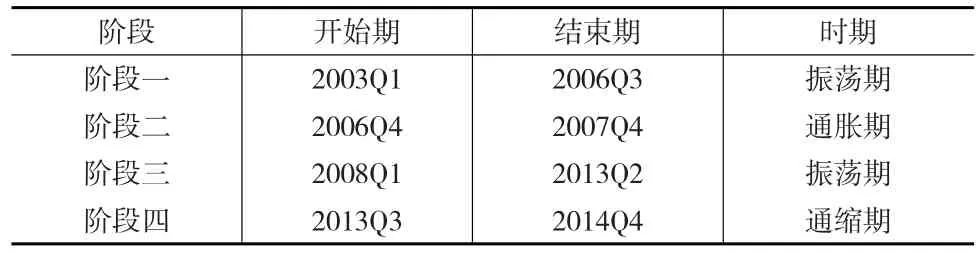
表4 五阶段通货膨胀特征
由表4可知在状态一时间段内,五省市通胀率的波动幅度较大,通胀和通缩交替出现,在阶段二,通胀率波动逐渐减小,而且呈现通货膨胀特征,阶段三是波动幅度最大的阶段,呈现先通缩后通胀特征,阶段四通胀率波动较小,但呈现通货紧缩特征。
下面对各个阶段进行分析,从中得到发生结构突变的原因。
阶段一:2003年1季度到2006年3季度之间的振荡特征是大规模投资导致对钢铁、水泥、橡胶等原材料和石油、煤炭等资源的需求过大,推高了该类资源价格的上涨造成的高通胀和政府为抗通胀而实施的稳健的货币政策而形成的低通胀交织的结果。
阶段二:从2006年4季度起,我国经济出现了一轮连续的较为明显的通货膨胀,其原因是高速增长的固定资产投资推动了工业原材料和资源价格的上涨,而农产品价格带动了物价上涨,从而加重了通胀压力,2007年全年CPI涨幅累计达4.8%,表现为通胀。
阶段三:虽然2008年第1季度的CPI总体涨幅达8.0%,但是随着2008年下半年全球金融危机的蔓延,我国CPI同比增长率持续下滑,经济增长速度正在放缓,中小企业面临生存困境,从而进入通货紧缩阶段。随后,政府实施积极的财政政策和宽松的货币政策时,进行了新一轮的基础建设投资,五省市很快从金融危机的影响中走出,扩大的国内市场需求、人民币连续升值及流动性转移等输入型通货膨胀等内外因素导致价格水平不断推高,形成了本阶段后期的通胀。
阶段四:随着经济刺激政策效果的不断延续,通胀压力也在逐渐减小,宏观经济政策从“稳增长、调结构”转向了“重视结构调整和增长质量”,GDP增速开始放缓,投资持续回落,居民收入增速放缓,出口持续改善,物价涨幅地位运行,呈现通缩特征。
4 结论
本文通过引入潜在的状态变量,利用贝叶斯方法在静态面板模型中同时检测存在的多个结构突变,得到了突变的后验分布,给出了在面板数据中同时估计多个结构突变的方法,推广了Geweke和Jiang(2011)[6]的方法。
选取2003年第1季度到2014年第4季度的北京、上海、江苏、浙江和广东的CPI通胀率季度数据作为研究对象,分析了经济环境变化冲击对通胀率的影响,发现2006年第4季度、2008年第1季度和2013年第3季度存在突变,通过对不同阶段的分析解释了发生突变的成因。利用贝叶斯方法对五省市通胀率存在的突变进行研究,得到以下两个结论:
(1)我国五省市的通胀率存在结构突变,在历史时期上表现出四次明显的变化特征。这说明随着我国经济结构改革的不断深化和宏观经济调控手段的逐步完善,通货膨胀系统内某些经济参数产生了明显的变化,从而发生了突变。检测结果表明突变发生在2006年第4季度、2008年第1季度和2013年第3季度。
(2)虽然我国在2005—2007年经济起伏较大,发生较快的物价上涨,但经模型检测表明这期间不存在变点,直到2008年1季度之后通胀率才发生变化。另外,我国政府在宏观经济调控中相机抉择的经济政策可能也是影响通胀率变化特征的一个因素。
[1]Hsiao C.Analysis of Panel Data[M].New York:Cambridge University Press,2003.
[2]白仲林.面板数据的计量经济分析[M].天津:南开大学出版社,2008.
[3]Chib S.Estimation and Comparison of Multiple Change Point Models[J].Journal of Econometrics,1998,(86).
[4]Pesaran H,Pettenuzzo D,Timmermann A.Forecasting Time Series Subject to Multiple Structural Breaks[J].Review of Economic Studies,2006,(73).
[5]Liao W.Structural Breaks in Panel Data Models:A New Approach[J].Working Paper,2008.
[6]Geweke J,Jiang Y.Inference and Prediction in a Multiple Structural Break Model[J].Journal of Econometrics,2011,163(2).
[7]张成思.中国通胀惯性特征与货币政策启示[J].经济研究,2008,(2).
[8]周平,王黎明.通货膨胀持久性研究综述[J].经济学动态,2011,(3).
[9]张成思,刘志刚.中国通货膨胀率持久性变化研究及政策含义分析[J].数量经济技术经济研究,2007,(3).

