基于恩格尔曲线的中国CPI偏差估计

曾先峰，章 洁

（西安外国语大学a.经济金融学院；b.资源环境与产业经济学研究中心，西安 710128）

0 引言

居民消费价格指数（CPI）反映居民购买生活用品和服务价格水平的变动情况，既是度量一个国家或地区通货膨胀率的核心指标，同时也是考察居民生活成本以及真实收入水平变动的关键，更关系到国家宏观政策的制定与实行，因此科学准确地估算CPI偏差对政府和政策决策者有重要的意义。但是在政府部门统计CPI的过程中存在四类偏差，即“替代偏差”、“质量改进偏差”、“新产品偏差”以及“购买途径偏差”[1]。

关于CPI偏差的测量，Hamilton-Costa[2]最早提出了利用恩格尔曲线估算CPI偏差。该方法从居民生活成本的角度出发，通过检验恩格尔曲线的稳定性来测定CPI偏差。由于该方法的简便性及其结果的直观性，被广泛用于不同国家不同时期的CPI偏差的估算。例如Beatty和Larsen（2005）[3]使用恩格尔曲线估计加拿大的CPI偏差；Gibson等（2004）[4]对俄罗斯的CPI偏差进行了估计；还有一些学者在这一方法上进行了延伸，例如Papalia（2006）估计了不同地区CPI偏差；Almas（2007）估计了购买了平价偏差。

中国估算CPI偏差的研究相对较少。与本文相关的文献，如许永洪和曾五一（2009）[5]利用1997—2006年城市收支统计数据研究了食品的恩格尔曲线和CPI偏差，结果表明除了1997年，中国官方CPI在其他年份不存在偏差。Nakmura等（2014）[6]则在该方法上有一些延伸，通过不同商品的恩格尔曲线解释了引起CPI偏差真正的原因。与上述文献不同，一是本文将研究的时间维度拓展到1995—2014年以捕捉金融危机之后CPI偏差的动态变化，二是使用了工具变量回归法，该方法能很好地避免普通最小二乘法带来的内生性问题，估算结果也更加准确。

此外，对中国统计数据的可靠性，在学术界历来就存在较大的争议。最新的一份研究报告（2016）[7]指出，中国GDP数据的可靠性排名为世界的第63位。因此，本文研究的另一层含义，即为验证中国官方统计数据的可靠性提供了依据。

1 理论模型与数据变量

1.1 理论模型

本文是基于 Nakamura（1996），Hamilton（2001）[1]和Costa（2001）[8]研究CPI偏差所采用的方法。Hamilton-Costa（2001）[1]是根据 Angus S.Deaton 和 Muellbauser（1980）［9］的理想需求系统（Almost Ideal Demand System，AIDS）提出了估算CPI偏差的核心方程：

其中，ω表示食品支出在家庭总消费支出中所占的比重；PF、PN、P分别表示不可观测的食品、非食品和所有商品的价格指数；Y表示名义家庭消费总支出水平；X表示家庭特征的一组变量；μ表示残差；下标t表示年份，j表示区域（城市），i表示家庭。且实际生活成本Pj，t是食品价格和非食品价格的加权平均：

一般情况下，食品价格指数PF、非食品价格指数PN和总价格指数的统计值与真实值之间有测量偏差，那么其形式可变为：

P0表示基期的真实价格，Π表示0到t期的价格累计变动百分比，E表示0到t期累计的价格观测偏差。食品和非食品的价格偏差与之类似。

假设CPI偏差不随地区变化而变化，将式（2）和式（3）带入理想需求系统——方程（1），并以小写字母p和y代替支出Y和价格P的对数形式，π和ε代替（1+Π）和（1+E）的对数形式，得到新的理想需求系统形式为：

假设不同的区域具有相同的价格偏差，则方程（4）可化为：

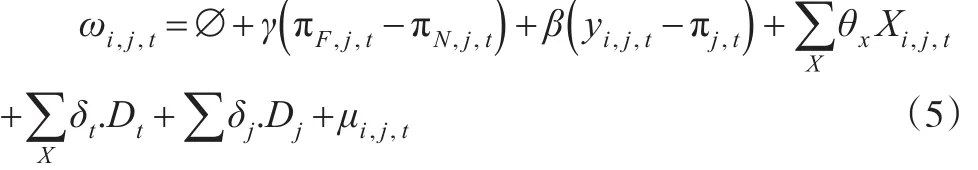
Dt和Dj分别是时间和地域的虚拟变量，在第t年的虚拟变量Dt等于1，其他年份等于0，在第j个地区Dj等于1，其他地区为0。δt和δj分别为Dt和Dj的系数。时间虚拟变量的系数对CPI偏差的估计十分重要。

时间虚拟变量Dt的系数为：

假设对于所有年份，食品偏差εF，t和非食品偏差εN，t之间的关系为固定比例（r）,即：εF，t=rεN，t，则CPI偏差可以表示为：

r是 εF，t和 εN，t的比例，即食品和非食品中CPI偏差的比例。α是生活成本指数中食品价格的份额。如果方程（7）中的γ或（1-r）趋近于0，那么该方程的最终表示极有可能是正确的。通常假设r=1，即食品和非食品的偏差具有相同的偏差程度。如果γ＜1,就会低估CPI偏差，反之则会出现高估，而这两种情况本文都不予考虑。

当γ或1-r趋近于0时：

因此，在时期t,累计的CPI偏差为：

1.2 变量与数据

本文使用1995—2014年30个（西藏除外）①西藏数据在1995—1997年数据缺失，且恩格尔系数与其他省份有很大差距，所以本文剔除了西藏的数据。省市的城镇住户的面板数据对我国的CPI偏差进行估算。数据主要来源于《中国统计年鉴》（1995—2015历年卷）、《中国城市（镇）生活与价格年鉴》（1995—2012历年卷）、《中国住户调查年鉴》（2013年、2014年）。

主要涉及的变量有：人均现金消费支出、人均食品消费支出、各种价格指数、人均可支配收入以及家庭人口数、有收入者人数、老年人抚养比、儿童抚养比等家庭特征变量。由于2014年消费支出的统计口径发生变化，为维持口径的一致性，2014年的消费支出是按照2013年新旧口径下的统计数据同比转换得到的。为分析近二十年来CPI的变动，本文选择将历年价格指数均转换为以1995年为基期的定基价格指数。非食品价格指数是由食品价格指数和CPI匡算得到。家庭人口数和有收入者人数缺失2013年和2014两个年度的数据，估算方法是根据2012年与2011年数据按照同比增长进行相应的推算所得。

方程（5）中的被解释变量为恩格尔系数（食品支出占总现金消费支出的比重），主要的解释变量包括真实的总消费支出、相对价格变化、家庭特征变量以及时间、地区虚拟变量。真实的总消费支出是由名义的人均现金消费支出和居民消费价格指数各自取对数后相减所得。食品和非食品的相关价格变化是由食品定基价格指数与非食品定基价格指数各自取对数后相减得到的，因为该变化会引起商品之间的替代效应从而会产生替代效应偏差，所以可以将该变量作为独立的解释变量。家庭人口数量的变化影响的是家庭人口规模的转变。Trevon D.Logan（2009）[10]说明了家庭规模变化会带来家庭规模经济效应，从而降低人均食品支出，因此若忽略家庭人口数量的影响，则会高估CPI偏差和生活成本。所以，本文将家庭人口数等特征变量均作为独立的解释变量以研究其对食品支出份额的影响。此外，本文还有一个控制变量——人均可支配收入，因为消费支出受收入的影响较大，故将人均可支配收入作为真实的总消费支出的控制变量进行工具变量回归分析。因为方程（5）是一个线性模型，所以可以使用最小二乘法（OLS）对模型进行回归估计。然而该方法不能消除解释变量可能存在内生性的问题，故应该同时使用工具变量法对方程进行回归估计，并将两种方法的回归结果进行对比分析。

2 实证结果

2.1 Hausman检验

本文依照经验分析判定真实的总消费支出为内生解释变量，并将人均可支配收入作为其工具变量。然而单纯的判断有可能产生错误致使得到的结果并非最有效的。Hausman检验提供了内生性检验的方法，通过比较普通最小二乘法（OLS）与工具变量回归（IV）估计量的统计值，从而进行判定是否存在内生性。检验结果显示，卡方值为83.68，接受原假设的概率p为0，说明在5%的显著水平下，可以拒绝外生性的原假设，即接受备择假设，认为真实的总消费支出为内生解释变量，且人均可支配收入为其工具变量。此外，Hausman检验结果也表明应当使用固定效应的工具变量回归得到估计量的统计值。为了更好地观察OLS与IV回归结果之间的不同，本文将同时进行两种回归分析，并将结果进行比较。

2.2 OLS与IV回归结果

表1是使用stata12.0对方程（5）进行OLS和IV估计的结果，由于时间和地区虚拟变量过于冗长，在回归结果中没有逐一显示。从整个方程的回归效果来看，两种方法的拟合优度分别为0.9258和0.9174，说明样本中绝大多数能被回归方程解释，从R2的角度看，城市统计数据的拟合效果不亚于Hamilton原文献（调整后的R2系数为0.538）。

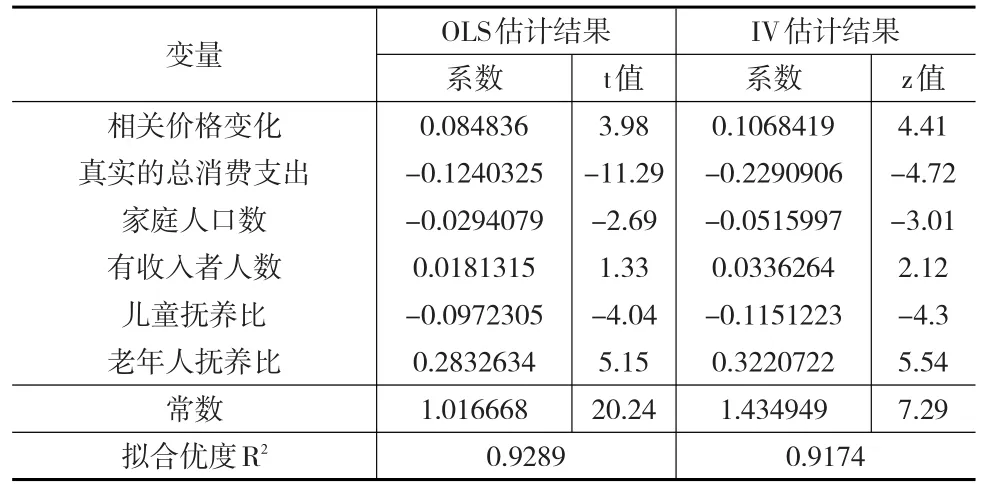
表1 方程(5)OLS和IV回归结果

由表1中回归结果对比可知，无论使用哪一种回归方法，真实家庭总支出的系数均为负的，说明食品支出份额随着人均总消费支出的上升而逐渐下降，这与恩格尔定理是一致的。食品相对于非食品的相关价格系数为正，意味着食品相对价格的变化会引起食品支出份额的同方向变化。家庭人口数的系数为负，即食品支出份额随着家庭人口的增加而下降，这与其他学者所得出的结论是相同的。

由Hausman检验可知，真实的消费支出存在内生性，因此将人均可支配收入作为其工具变量带入回归方程，对比两种回归结果，使用IV估计出来的真实的消费支出水平前的系数（-0.229）的绝对值要比OLS估计值（-0.1240）大且更显著，说明使用IV估计出来的消费支出水平对食品支出份额的影响更大。类似的，从IV和OLS的其他变量的估计值比较来看，使用工具变量估计值所表现出的对食品支出份额的影响更大。

2.3 基于恩格尔系数变动的中国CPI偏差估算

方程（5）中加入时间和地区虚拟变量的回归结果显示，OLS估计结果中的时间虚拟变量均显著，地区虚拟变量除了北京、天津、江苏、浙江、江西、湖北、四川、贵州、青海这9个省市的系数不显著，其他21个省市的系数均高度显著。这一方面说明相似家庭结构（省市）、相同价格和消费支出水平家庭在不同年份都有一定程度的偏差，另一方面也说明不同地区的恩格尔系数不同，地域的差异性较为明显。而IV估计结果显示，1995—2002年的时间虚拟变量高度显著，2003—2014年均不显著，这说明2003—2014年我国的CPI不存在偏差。对于地区虚拟变量，只有北京、天津、江苏、安徽、江西、四川、贵州这7个省市的系数不显著。两种回归结果均说明了中国的CPI存在偏差。图1显示的是恩格尔曲线变动趋势图。

图1 恩格尔系数变动趋势图

首先，从两种模型的回归结果来看，就单个曲线的变化趋势而言是不符合恩格尔定理的，即食品支出份额随着时间的推移表现出逐渐减小的趋势。其中2004年、2008年、2011年与上年相比均有所上升，尤其是2008年上升幅度最大。这可能是由于物价和收入等其他因素变动使得居民为了维持相同效用水平生活及时调整了生活支出的构成。其次，根据OLS估计调整的恩格尔系数比原始的恩格尔系数变化幅度更大，而IV估计下调整的恩格尔系数要明显平缓一些，且在2004年后和原始数据保持一致。两种方法估计出来的恩格尔系数与原始的有差异，正说明了我国的CPI是存在偏差的。

此外，大部分城市虚拟变量也显著，说明中国城市恩格尔系数的地域差异也是很明显的。如上海、广东、福建等8个城市的恩格尔系数与全国相比有向上的偏差，河南、山东、陕西等13个城市的恩格尔系数则有向下的偏差。由于各个城市采用的统计口径是一致的，城市之间恩格尔系数的差异可能是由于不同地区居民的消费习惯的差异所引起的。

2.4 CPI偏差大小的估算

依据公式（9）计算得出以1995年为基期的消费者价格指数偏差和真实生活成本指数如表2所示。

表2 1995—2014年CPI和调整偏差后的CPI

OLS回归结果表明我国1995—2014年间的定基CPI指数与生活成本指数之间存在一定的正向偏差，即所公布的CPI指数高于居民实际生活费用指数。通过式（9）计算得出各个年份的累积CPI偏差，每年CPI偏差变动范围为0.09和0.51，平均每年变动0.398个百分点，与官方CPI平均每年2.599个百分点的变动相比，大概六分之一的CPI变动是由CPI偏差引起的。IV回归结果则表明，在2003年之前，每年都存在正的偏差，且每年偏差均小于OLS估算的偏差大小，但在2003年后，由于时间虚拟变量均不显著，因此可认为官方CPI并不存在偏差。

雷怀英（2016）[11]估算的以2000年为基年的定基CPI偏差结果表明，只有2004年、2005年、2007年、2008年、2009年、2011年、2012年存在负的CPI偏差，其他年份均存在正的CPI偏差，年平均CPI偏差约0.06个百分点。本文计算得出的CPI偏差与国内学者相比，差异较大。但与国外学者的研究相比，如Hamilton（2001）[2]估算的美国1982—1991年CPI偏差国际上测算的年平均CPI偏差约为 0.67 个百分点，John Gibson（2007）[4]估算的俄罗斯1994—2001年的CPI偏差范围是0.64～0.87个百分点，本文对中国CPI偏差的估算结果在合理的范围内变动，这也可以间接的论证了中国的官方数据大体上是可靠的。

3 调整偏差后的实际可支配收入与消费支出

真实的收入水平与消费支出是衡量一国福利水平的重要指标。如果CPI存在偏差，必然影响由名义量经CPI平减后的真实量的准确性与可靠性，从而可能对收入和消费指标产生误判。本文的研究发现，官方公布的CPI数据存在向上的偏差，对偏差进行调整后的CPI数据高于官方公布的数据。从而，根据官方数据核算的真实收入和消费支出可能存在高估。图2是根据官方数据对CPI偏差进行调整后CPI数据核算的真实城镇居民人均可支配收入与消费支出数据。

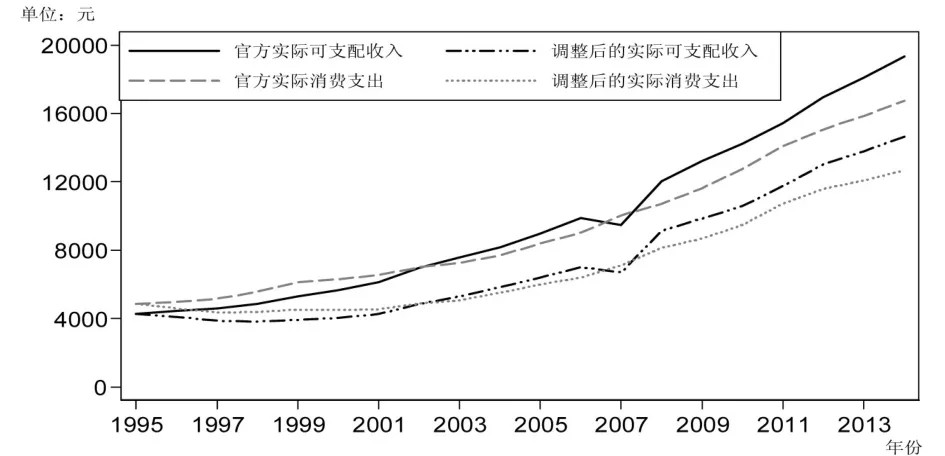
图2 实际人均可支配收入与消费支出趋势图

图2表明，根据调整后的CPI估算的真实收入和消费支出要低于根据官方数据所估算的相应量，而且在变化趋势表现出高度的一致性。与调整后相比，官方的真实收入和消费支出在1995—2014年高估约23.76个百分点。

4 结论

本文通过将Hamilton—Costa方法引入中国CPI偏差估计，利用现有城市价格和收支统计数据，在假定恩格尔定理存在的情况下，得到两点主要的结论：

第一，实证表明，以1995年作为基年，1996—2014年中国城市的定基CPI与生活成本指数之间都存在向上偏差，偏差幅度为0.09～0.51个百分点之间，年均CPI偏差约0.398个百分点。CPI偏差会误导政府、企业及个人的决策，同时还会引起公众对CPI可靠性的质疑。调整后的CPI数据对名义变量进行调整，表明我国实际的人均收入和消费支出被高估了，平均每年高估约23.76个百分点。

第二，中国恩格尔系数波动较大，且没有表现出随时间的推移而逐渐减少的趋势，平均每年大约有0.07个百分点的向下偏差，这可能是由于物价等其他因素变动所引起的居民为维持相同效用水平的生活经常需要调整生活支出构成。此外，对不同地区的恩格尔系数进行对比发现，上海、广东、福建等8个城市的恩格尔系数与全国相比有向上的偏差，河南、山东、陕西等13个城市的恩格尔系数则有向下的偏差，这种恩格尔曲线的差异主要是由于消费的地域特征引起的，不能以恩格尔系数简单的对比来评价不同城市的发展水平。

由于编制理论和方法的差异，导致以固定篮子编制的CPI和生活成本指数之间会存在明显的差异，这种差异会让人们从生活成本的角度明显地感知到CPI是存在偏差的。因此，我国应该及时对CPI中存在的偏差进行估算和分析，以便对其编制方法进行针对性的改进，从而提高CPI等官方数据的可靠性。

[1]Hausman J.Sources of Bias and Solutions to Bias in the CPI[J].Jour⁃nal of Political Economy,2003,(17).

[2]Hamilton B W.Using Engle’s Law to Estimate CPI Bias[J].The Amer⁃ican Economic Review,2001,91(3).

[3]Betty T K M,Larsen E R.Using Engle Curves to Estimate Bias in the Canadian CPI as a Cost of Living Index[J].Canadian Journal of Eco⁃nomic,2005,38(2).

[4]GibsonJ,StillmanS,et al.CPI Bias and Real Living Standards in Rus⁃sia During the Transition[J].Journal of Development Economics,2007.

[5]许永洪，曾五一.基于中国城市统计数据的CPI偏差估计[J].统计研究，2009,（4）.

[6]Nakamura E,Steinsson J,Liu M.Are Chinese Growth and Inflation Too Smooth?Evidence From Engle Curves[J].National Bureau of Eco⁃nomic Research,2014.

[7]全球GDP数据可靠程度排名：瑞士居首海地垫底[R].数独，2016,（1）.

[8]Costa D L.Estimating Real Income in the United States From 1888 to 1994:Correcting CPI Bias Using Engle Curves[J].Journal of Political Economy,2001,109(6).

[9]Deaton A,Muellbauer J.An Almost Ideal System[J].The American Economic Review,1980,70(3).

[10]Logan T D.Are Engle Curve Estimates of CPI Bias Biased[J].Histor⁃ical Methods:A Journal of Quantitative and Interdiscriplinary Histo⁃ry,2009,42(3).

[11]雷怀英,王童,赵文娅.基于Hamilton-Costa模型的CPI偏差测定研究[J].经济问题，2016，(4).