中国工业分行业能源CES生产函数估计与选择

毕超，何旭波

（1.陕西师范大学国际商学院，西安710119；2.云南大学发展研究院，昆明650091）

0 引言

随着经济增长带来的资源和环境问题在中国变得日益严峻，制定科学有效的节能减排政策日益受到各方的重视。为此，经济学中通常使用可计算一般均衡（CGE）方法模拟能源环境政策的影响，进而为制定和评判节能减排政策提供决策依据[1]。近年来CGE方法在我国的应用日益广泛，但该方法在实践应用中也备受质疑，而根源则是其用于描述生产者行为的常替代弹性（CES）函数设定存在较大的主观性和任意性[2-4]。因此，如何科学的设定CGE方法中的CES函数形式并度量替代弹性，就成为了能否合理应用CGE方法，并科学制定和评价节能减排政策的关键。

当前文献中主要有三种估计CES函数的方法：一是直接估计生产函数法[5]，虽然有学者使用该方法证明了中国政策模拟适宜使用（KE）L函数形式[6]，但是该方法难以同时估计替代弹性和要素增强性技术进步，其希克斯中性技术进步的假设也与现实相差甚远。二是标准化供给面系统法[7]，该方法可以估计要素增强性技术进步，但难以处理多投入要素的生产系统，因而多用于分析资本和劳动之间的替代弹性[8]。三是估计一阶条件法[9]。该方法的优点在于可以利用合成品的份额变化代替其量价变化，进而很容易处理包含多投入要素的生产系统[10]。考虑到上述三种估计方法的适用性，及目前CGE建模的一大趋势是越来越细化生产部门的分类，本文拟借鉴估计一阶条件法估计中国工业分行业的三要素CES函数，并以所有工业二位码行业为研究对象，同时允许存在要素增强型技术进步，以提升所估计CES函数的适用性。

1 计量模型设定

早期的CES函数只包含两种投入要素[11]，之后被扩展至包含多种投入要素[12]；Sato（1967）进一步开发出一类称为嵌套形式的CES函数（Nested CES）[13]，并得到广泛应用。在只有两种投入的CES函数中，两种投入具有同等重要的地位，而在多投入CES函数中，首先以组合方式将多个要素合并为一个代表性合成品，再以单一合成品的形式进入函数，从而实现多投入到两种投入的转换。在此背景下，不同的组合方式意味着不同的经济含义，而且以此为基础估算的结果通常也会存在较大差异。就资本（K）、劳动（L）和能源（E）三种投入要素而言，共有（KL）E、（KE）L、（LE）K和KLE[13]四种组合形式，并对应着具体的函数形式。此处仅以（KL）E形式为例说明，见式（1）和式（2）：

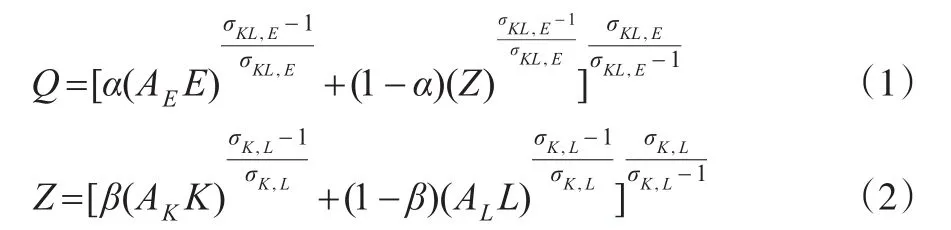
其中，AK、AL、AE分别表示资本、劳动和能源三种要素的增强型技术进步，三者相等表示函数中的技术为希克斯中性技术进步；Q表示最终产品，Z表示资本-劳动合成品；σK，L表示资本与劳动间的替代弹性，σKL，E表示合成品与能源间的替代弹性，二者相等时等价于KLE形式；α和β为份额参数。

若用式（1）和式（2）表示代表性厂商的生产函数，则在成本最小化目标下得到厂商的一阶最优条件函数，由此函数取对数，并进行一阶差分后，得到式（3）至式（6）：

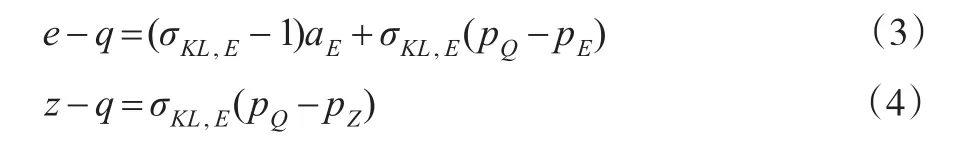
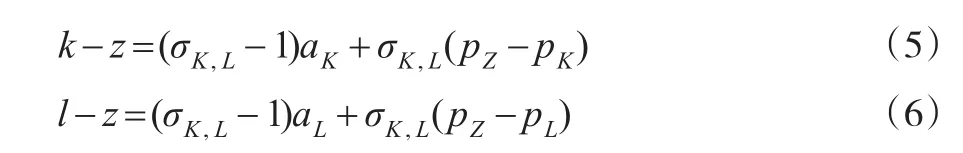
其中，aK、aL、aE分别表示资本、劳动和能源三种投入要素的增强型技术进步率；k、l、e、z、q分别表示资本存量、劳动投入、能源消费、合成品以及最终产品产量的变化率；pK、pL、pE、pZ和pQ分别表示资本、劳动、能源、合成品和最终产品的价格变化率。

考虑到无法直接观测到z和pZ的值，因此在构建计量模型时，在式（5）的两边同时加上pK-pQ-(pZ-pQ)，得式（7）：

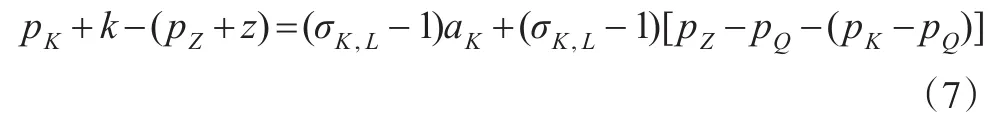
在式（4）的两边同时加上pZ-pQ，整理后得式（8）：

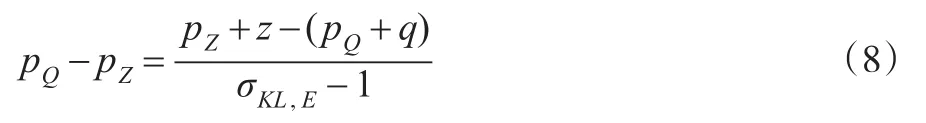
将式（8）代入式（7）的右边，整理后得式（9）：

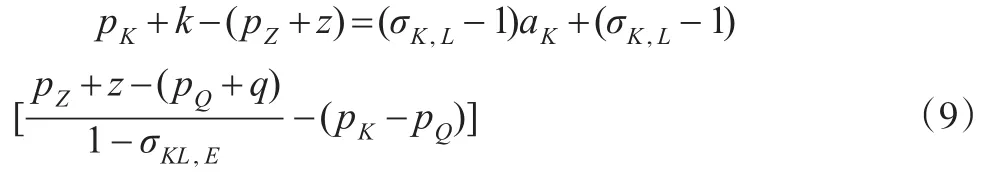
其中，式（9）等号左边的项表示资本在合成品中的份额变化率，而右边的pZ+z-(pQ+q)表示合成品在最终产品中的份额变化率。由CES函数的一次齐次性和欧拉定律可知z的收入等于资本和劳动的报酬之和，故可算出合成品的份额变化率。以相同的方法处理式（6），整理后得式（10）至式（12）：

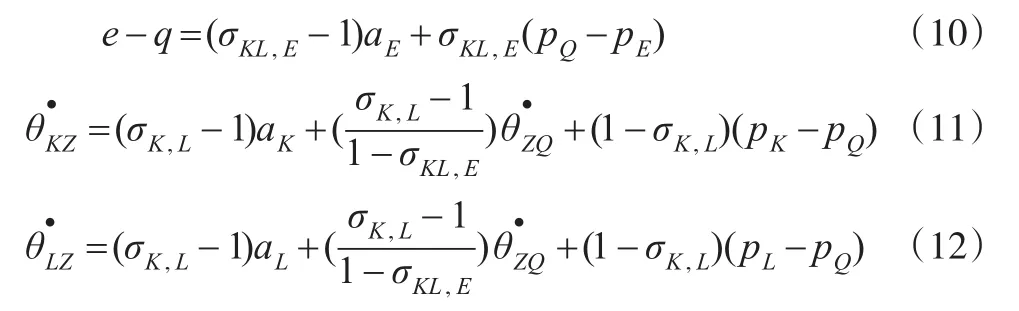
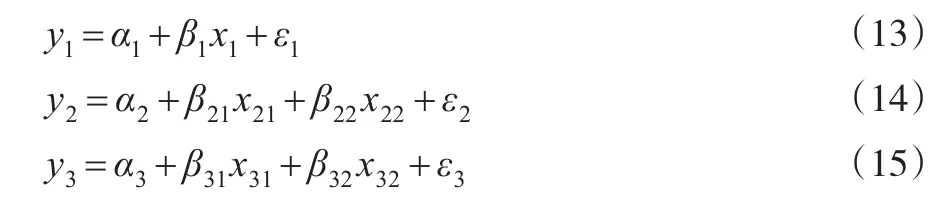
为了与式（10）至式（12）保持一致，还需加入下列限制条件：

式（13）至式（17）即为（KL）E形式对应的计量模型，（KE）L和（LE）K对应的计量模型与此类似。上述模型设定方式更具灵活性，能够方便地对以下三个原假设进行检验：（1）若β21=β31=1，则嵌套形式的CES函数退化为KLE形式；（2）若β1=1且β22=β32=0，则所有替代弹性均为1，生产函数变为C-D形式；（3）若，则有aK=aL=0，对应的技术进步为希克斯中性，能源增强型技术进步等于TFP。

2 数据来源及处理

由历年统计年鉴可知，中国工业分行业数据的分类标准及统计口径在1980—2015年间并不统一。为联合估计式（13）至式（17），在陈诗一（2011）[14]的基础上构建了1980—2015年中国工业部门37个二位码行业的投入-产出数量和价格数据库，其中，以工业增加值度量部门产出，以资本存量、就业人数和能源消费总量度量部门投入。1980—2008年投入-产出数据直接来自陈诗一（2011）[14]的研究成果，2009—2015年投入-产出数据是借鉴陈诗一（2011）[14]的方法估算而来。

其中，2009—2015年分行业增加值的估算涉及三个步骤：首先利用2007年的增加值数据，及相应年份的增加值增速计算出2009—2015年规模以上工业分行业的名义增加值；其次根据《中国价格统计年鉴2016》中各行业的工业品出厂价格指数将名义增加值平减为1990年货币单位表示的实际值；最后将《中国经济普查年鉴2008》中全部工业总产值与相同年份规模以上工业部门总产值之比作为口径调整系数，将实际增加值调整至全部工业行业。

分行业的产出价格方面，1985—2015年的数据来源于《中国城市（镇）生活与价格年鉴2011》《中国价格统计年鉴2016》，1980—1984年的数据来源于《中国统计年鉴1993》。

分行业资本存量和资本价格方面，累计折旧、固定资产原值和固定资产净值等估计资本存量的原始数据来自《中国工业经济统计年鉴》，以新增固定资产表示投资，利用固定资产投资价格指数将2009—2015年的新增固定资产折算为以1990年价格表示的实际值，调整口径后使用永续盘存法计算2009—2015年各个工业部门的资本存量。基于资本的边际收益等于边际成本的原则估计资本的边际收益率，以资本的边际收益率度量资本价格[15,16]。数据主要来源于相关年份的《中国工业经济统计年鉴》和《中国统计年鉴》。

分行业劳动投入和工资方面，2009—2015年全部工业的就业数据来自于2010—2016年的《中国统计年鉴》，并以《中国经济普查年鉴2008》中的全行业就业数据与相同年份规模以上行业数据之间的比值作为口径调整系数进行调整。基于相关文献，本文在估计出分行业就业人员的实际工资总额基础上，进一步构造分行业就业人员的平均工资。

分行业能源消费与能源价格方面，2009—2015年分行业的能源消费数据来自于2011—2016年《中国统计年鉴》，然后按照首先构造能源价格指数，之后估计某一年份的能源平均价格，最后利用价格指数将能源平均价格“映射”到整个样本期[16,17]的思路，估计各部门的能源消费价格指数。

3 估计结果及讨论

3.1 不同函数形式下替代弹性的估计

本文利用Stata12.0软件首先对式（13）进行估计，然后以式（16）和式（17）为约束条件，联合估计式（14）和式（15）。因为多层嵌套CES函数具有弱可分性，所以从最顶层的生产函数进行估计，由此得到的结果并不会受到太大影响[9]。不同函数形式下替代弹性的估计结果如表1所示。

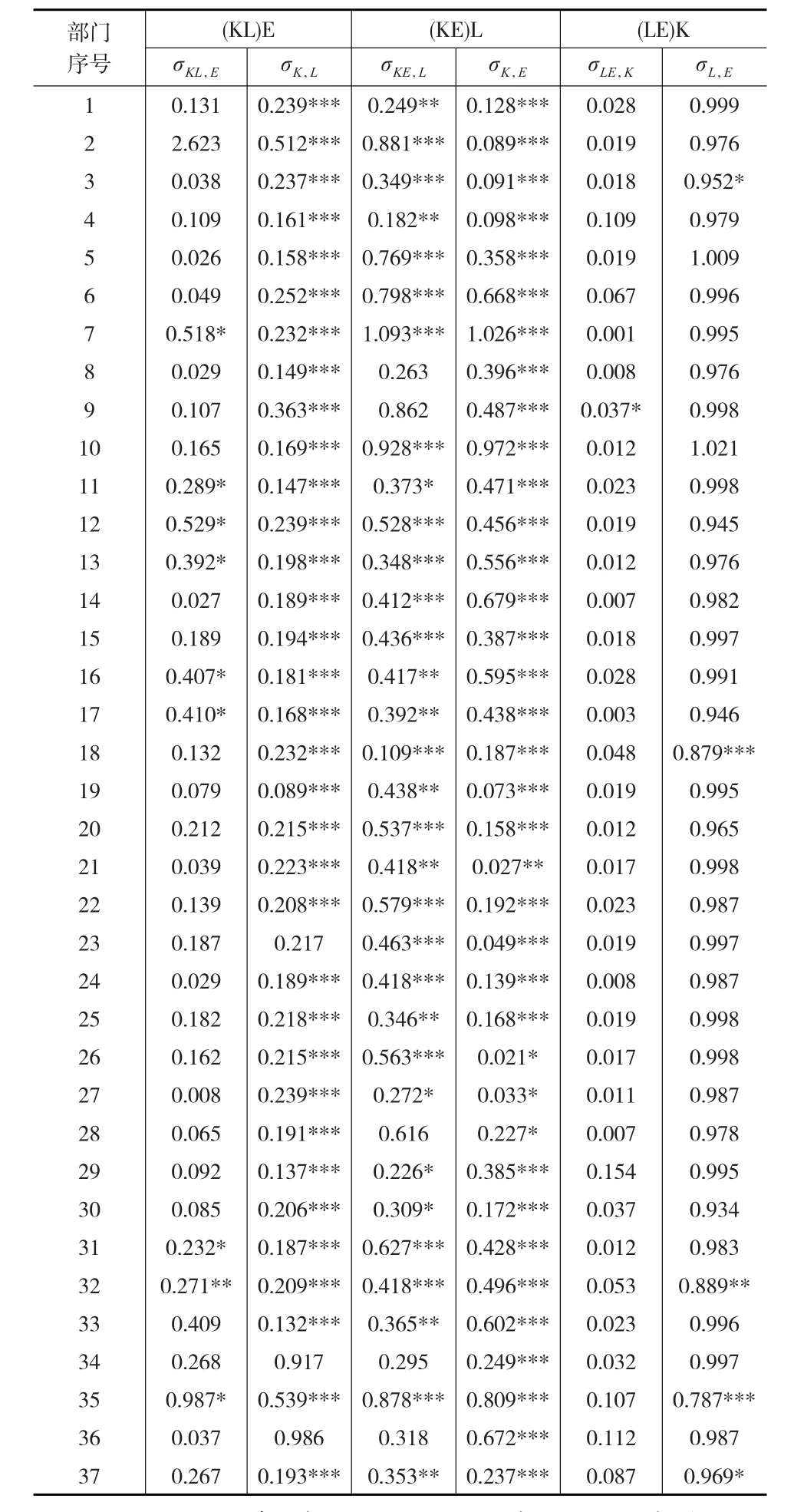
表1 不同生产函数形式下的替代弹性估计

(KL)E函数形式下，σK，L的估计值为0.089～0.986，估计值最小的部门是“化学原料及制品制造业”，最大的部门是“自来水的生产和供应业”；其中，除“塑料制品业”、“电力、蒸汽热水生产供应业”和“自来水的生产和供应业”等部门外，其他部门的估计值均在1%的水平上显著；σKL，E的估计值为0.008～2.623，估计值最小的部门是“金属制品业”，最大的部门是“石油天然气开采业”；其中，仅有“食品制造业”、“服装及纤维制品”、“皮羽及其制品”、“印刷业”、“文教体育用品”、“电子机械及器材制造业”、“计算机电子通信设备制造业”和“燃气的生产和供应业”等部门的估计值通过了显著性检验；上述替代弹性估计值均显著的部门中，σKL，E均大于σK，L，可能的原因是这些部门生产对能源的依赖较小。

（KE）L函数形式下，σK，E的估计值为0.021～1.026，估计值最小的部门是“有色金属冶炼及压延加工业”，估计值最大的部门是“食品制造业”；其中，大部分部门的估计值均在1%的水平上显著，仅有“有色金属冶炼和压延业”、“金属制品业”和“通用设备制造业”四个行业的估计值在10%水平上显著；σKE，L的估计值为0.109～1.093，估计值最小的部门是“石油加工及炼焦业”，估计值最大的部门是“食品制造业”；其中，除“饮料制造业”、“烟草加工业”、“通用设备制造业”、“电力、蒸汽及热水生产供应业”和“自来水的生产和供应业”未能通过显著性检验外，其余部门的估计值均显著；上述估计值均显著的部门，除“食品制造业”外，其余部门的σKE，L均大于σK，E，说明能源在这些部门生产中的重要性和必要性；此外，σK，E在各部门间的分布存在明显差异，能耗大的行业σK，E的估计值较小。

（LE）K函数形式下，σL，E的估计值为0.787～1.021，估计值最小的部门是“燃气的生产和供应业”，估计值最大的部门是“非金属矿采选业”；其中，仅有“黑色金属矿采选业”、“石油加工及炼焦业”、“计算机电子通信设备制造业”及“燃气生产和供应业”的估计值显著，且估计值很接近1，说明这些部门内部劳动和能源之间的互补性较弱；σLE，K的估计值为0.001～0.154，估计值最小的部门是“纺织业”，估计值最大的部门是“专用设备制造业”；其中，仅有“烟草加工业”在10%的显著性水平上显著。

从替代弹性估计值的显著性上判断，（KE）L函数形式可能较适合中国工业部门。将表1估计结果和已有的研究结果相比较[6,18]，发现仅估计全国水平的CES函数可能会忽略不同行业的异质性：对于高能耗部门，可能会高估σK，E和σKE，L；而对于低能耗部门，则存在低估σK，E的可能性。主要原因可能是在采用全国层面的宏观数据时，不同部门间投入要素的互补性被低估了；此外，估计全国水平的CES函数通常采用希克斯中性技术进步假设，而式（1）和式（2）则包括了要素增强型技术进步，考虑了生产要素存在效率改善的可能性。

3.2 要素增强型技术进步率的估计值

由于(KE)L形式较符合中国工业部门的实际情况，本文仅估算(KE)L函数形式下的要素增强型技术进步率①以能源增强型技术进步率aE为例，在估计出各α和β的值后可求出aK、aL和aE的值，但要保证估计的精度，还需计算出a的估计标准差。假设(σK，E-1)和a相互独立，由方差计算公式可知：Std(a)=，其中，std(·)、VAR(·)和E(·)分别表示变量的标准差、方差和均值。因篇幅所EE限，本文仅报告a的估计值。。估计结果见图1。

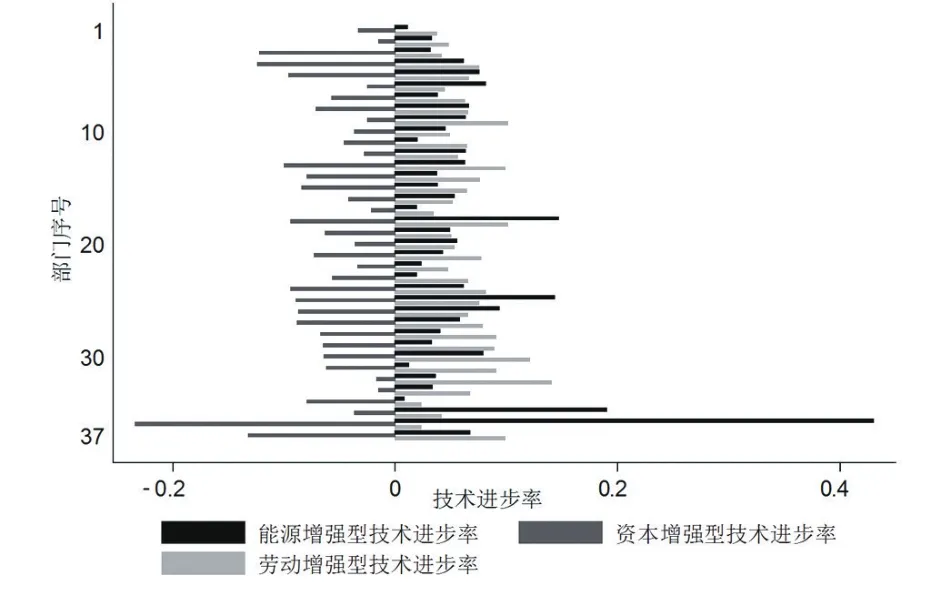
图1 中国工业分行业要素增强型技术进步率

样本期内，能源增强型技术进步率aK的估计值为0.078～0.426，aK的估计值最小的部门是“电力、蒸汽热水生产供应业”，最大的部门是“自来水的生产和供应业”；正的估计值说明能源的有效投入增加，或者说样本期内存在能源节约型技术进步[19]；其中，除“电力、蒸汽热水生产供应业”、“燃气的生产和供应业”及“自来水的生产和供应业”等行业外，其他部门的估计值均在10%水平上显著，且高能耗部门具有较大的能源增强型技术进步率。

资本增强型技术进步aK估计值为-0.013～-0.236，aK的估计值（绝对值）最小的部门是“石油和天然气开采业”，最大的部门是“自来水的生产和供应业”；负的资本增强型技术进步率说明工业部门存在资本使用型技术进步[20]；其中，除“燃气的生产和供应业”外，其他部门的aK均在10%水平上显著。Acemoglu（2002）[21]认为，当资本存量处于稳态值之下时，模型会内生出资本使用型技术进步。考虑到中国属于发展中经济体，资本存量应处于稳态值之下；另一方面，资本使用型技术进步意味着，资本投入增加在导致边际报酬递减的同时，也会带来技术进步水平的提升，因而可以较好的解释中国经济高投资与高增长并存的现象。

劳动增强型技术进步率aL的估计值为0.026～0.142，aL的估计值最小的部门是“自来水的生产和供应业”，最大的部门是“计算机电子通信设备制造业”；其中，除“自来水的生产和供应业”外，其他部门aL的估计值均在10%水平上显著。高能耗部门aL的估计值低于其他工业部门。

3.3 假设检验

本文将通过设计如下原假设，进而检验(KE)L函数形式下估计值的可信性：

H1：CES函数采用KLE形式；

H2：CES函数采用C-D形式；

H3：CES函数为希克斯中性技术进步。

H3-a：资本、劳动增强型技术进步率相同，即aK=aL；

H3-b：能源、劳动增强型技术进步率相同，即aE=aL；

H3-c：资本、能源增强型技术进步率相同，即aK=aE。

其中，原假设H3实际上检验的是资本增强型技术进步率aK和能源增强型技术进步率是否同时为零，而劳动增强型技术进步率aL显著地异于零。故拒绝原假设H3在严格意义上并不能保证各部门的技术进步率为中性，原假设H3被拒绝也有可能是以下原因：（1）资本、劳动和能源增强型技术进步率均为零；（2）劳动增强型技术进步率显著地异于零，但资本、能源增强型技术进步率不同时为零。因此，在假设检验H1至H3的基础上，另外设计三个假设检验以检验各工业部门的技术进步是否显著地为希克斯中性形式。

检验结果见下页表2。其中，除“电力、蒸汽与热水的生产和供应业”在10%的显著性水平上不能拒绝C-D函数的原假设外，其他所有部门均在10%的显著性水平下拒绝了KEL、C-D函数和中性技术进步的原假设，而“电力、蒸汽与热水的生产和供应业”在15%的显著性水平上拒绝了C-D函数的原假设；所有的工业部门均在10%的显著性水平上拒绝了原假设H3-a，说明资本、劳动增强型技术进步率不相同；仅有“纺织业”、“皮羽及其制品业”和“家具制造业”等11个部门在10%的显著性水平上拒绝原假设H3-b，其他部门则在15%的显著性水平上拒绝aE=aL的原假设；除“医药制造业”、“塑料制品业”、“金属制品业”以及“燃气的生产和供应业”外，其他部门均在10%的显著性水平上拒绝了aK=aE的原假设，而上述几个部门在15%的显著性水平上拒绝了原假设H3-c。

4 结论及政策含义

本文运用1980—2015年中国工业分行业投入产出数据，对中国工业部门的CES函数形式进行了估计，估计结果发现：（1）从替代弹性估计值的显著性上判断，（KE）L函数形式比（KL）E和（LE）K形式更符合中国工业分行业的实际情况。（2）（KE）L函数形式下，37个细分行业的资本-能源替代弹性范围为0.021～1.026，资本能源合成品与劳动的替代弹性范围为0.109～1.093，能源、资本与劳动的替代弹性在行业间存在很大差异，仅估计工业总体层面CES函数会忽略不同行业的异质性。（3）除“电力、蒸汽与热水的生产和供应业”在10%的显著性水平上不能拒绝C-D函数的假设外，其他36个行业均在10%的显著性水平下拒绝了KEL、C-D函数和中性技术进步的原假设。（4）（KE）L函数形式下，中国工业分行业的能源增强型技术进步率为0.78%～42.6%，资本增强型技术进步率为-1.3%～-23.6%，劳动增强型技术进步率为2.6%～14.2%，要素增强型技术进步率在行业中同样存在很大差异。

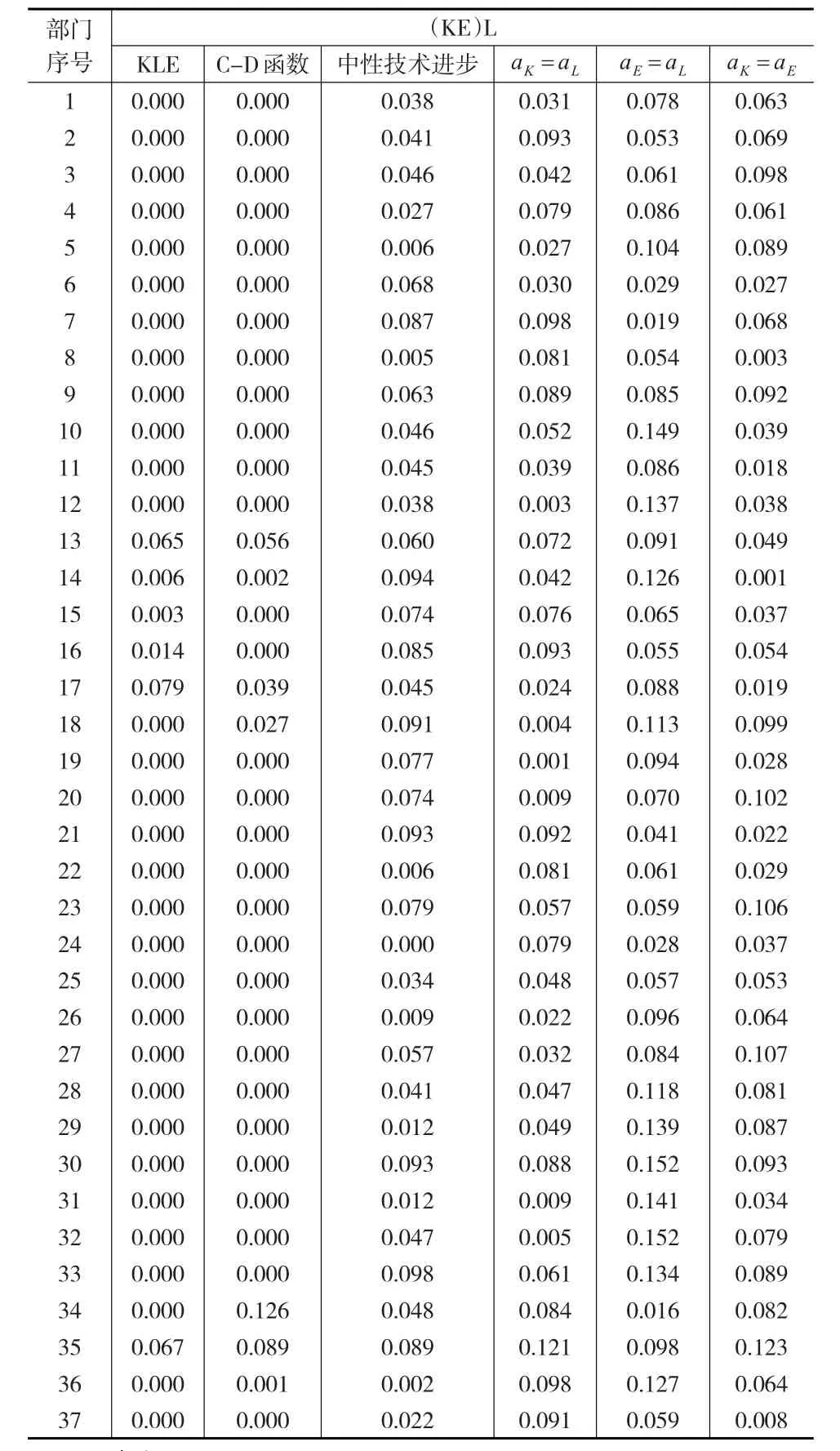
表2 （KE）L函数形式下的假设检验结果

本文的研究结论一方面为CGE建模提供了科学依据，另一方面也具有鲜明的政策含义：（1）从资本-能源替代弹性的角度来看，若资本-能源替代弹性大于1，低碳发展和经济增长就能并行不悖，因此提升资本-能源替代弹性本身就可以作为政策目标之一。但就本文的估计结果来看，在37个细分行业中，仅有1个行业资本-能源替代弹性大于1，大于0.5的也仅有8个行业。（2）从要素增强型技术进步率的角度来看，绝大部分细分行业的技术进步都属于能源节约型技术进步，但是节约的程度有较大差异，而且一半以上的行业能源节约型技术进步率在0.1以下，特别是高耗能部门的能源节约型技术进步率相对较高，而非高耗能部门的能源节约型技术进步率相对较低，反映了目前节能减排过程中在重视高耗能部门治理的同时，可能对非高耗能部门的治理相对忽略，今后若能加强非高能耗部门的能源效率治理或许能更有效地提升节能减排政策效果，这为后续节能减排政策的制定提供了一个有价值的方向。

[1] 陈诗一.能源消耗、二氧化碳排放与中国工业的可持续发展[J].经济研究,2009,(4).

[2] Popp D.ENTICE:Endogenous Technical Change in the DICE Model of Global Warming[J].Journal of Environmental Economics and Man⁃agement,2004,(48).

[3] Edenhofer O,Bauer N,Kriegler E.The Impact of Technological Change on Climate Protection and Welfare:Insights From the Model MIND[J].Ecological Economics,2005,(54).

[4] Bosetti V,Carraro C,Galeotti M,et al.WITCH:A World Induced Tech⁃nical Change Hybrid Model[J].Energy Journal(Special Issue:Hybrid Modelling of Energy Environment Policies:Reconciling Bottom-up and Top-down),2006,(27).

[5] Kmenta,J.On Estimation of the CES Production Function[J].Interna⁃tional Economic Review,1967,8(2).

[6] 吕振东,郭菊娥,席酉民.中国能源CES生产函数的计量估算及选择[J].中国人口·资源与环境,2009,(4).

[7] Klump R,McAdam P,William A.The Normalized CES Production Function:Theory and Empirics[R].European Central Bank Working Paper,No.1294,2007.

[8] León-Ledesma M A,McAdam P,William A.Identifying the Elastici⁃ty of Substitution With Biased Technical Change[J].American Eco⁃nomic Review,2010,100(4).

[9] Van der Werf E.Production Functions for Climate Policy Modeling:An Empirical Analysis[J].Energy Economics,2008,30(6).

[10] De Cian E.Factor-Augmenting Technical Change:An Empirical Assement[R].Fondazione Eni Enrico Mattei and School of Advanced Studies in Venice Working Paper,No.18,2009.

[11] Arrow K J,Chenery H B,Minhas B S,et al.Capital-Labor Substitu⁃tion and Economic Efficiency[J].The Review of Economics and Sta⁃tistics,1961,43(3).

[12] Uzawa H.Production Function With Constant Elasticities of Substi⁃tution[J].Review of Economics Studies,1961,(9).

[13] Sato,K.A Two-Level Constant-Elasticity-of-Substitution Produc⁃tion Function[J].Review of Economic Studies,1967,(34).

[14] 陈诗一.中国工业分行业统计数据估算:1980—2008[J].经济学(季刊),2011,(3).

[15] 鲁成军,周端明.中国工业部门的能源替代研究——基于对AL⁃LEN替代弹性模型的修正[J].数量经济技术经济研究,2008,(5).

[16] 国涓,郭崇慧,凌煜.中国工业部门能源反弹效应研究[J].数量经济技术经济研究,2010,(11).

[17] 陶小马,邢建武,黄鑫,周雯.中国工业部门的能源价格扭曲与要素替代研究[J].数量经济技术经济研究,2009,(11).

[18] 魏玮,何旭波.中国工业部门的能源CES生产函数估计[J].北京理工大学学报：社会科学版,2014,16(1).

[19] Sue W I.Induced Technical Change in Computable General Equilib⁃rium Models for Climate-Change Policy Analysis[D].PhD disserta⁃tion,Massachusetts Institute of Technology.Engineering Systems Di⁃vision,2001.

[20] Temple J.The Calibration of CES Production Function[J].Journal of Macroeconomics,2012,34(2).

[21] Acemoglu D.Directed Technical Change[J].Review of Economic Studies,2002,69(4).