小样本下指数分布可靠性参数估计方法的比较

罗修辉，韦程东，王一茸

（广西师范学院 数学与统计学院，南宁 530023）

0 引言

大数定律决定了传统的概率统计在进行可靠性分析时，需要有足够的样本容量来对未知分布特征进行估计，然而在工程实践中、特殊产品寿命分析或者在对高科技新型装备进行可靠性分析时,往往产生的是珍贵的小样本（在工程实践中，一般以样本容量n≤30为小样本），此时数据少的问题就显得极为突出。在此情况下，如果将大样本理论引用到对小样本可靠性分析时，显然会导致估计精度降低,使得可靠性分析不那么可靠。因此，如何在小样本情况下估计所研究未知分布的可靠性参数是一个急需解决的问题。

目前，小样本可靠性参数估计主要有Bayes方法、Bayes Bootstrap方法和蒙特卡罗仿真方法[1-4]。但大多数文献都是基于正态分布进行研究的，而在大多情况下典型的可靠性分布都是非正态的，因而基于其他分布下去研究可靠性参数估计是非常必要的,本文正是在小样本条件下研究指数分布可靠性的参数估计。

1 小样本可靠性参数评估的传统方法

1.1 问题的提出

当产品可靠性能指标X～Exp(λ)且任务要求X≤x时,产品可靠度可由式（1）计算：

其中F(x)为指数分布的分布函数，I{A}表示A的示性函数。

由于参数λ真值无法获取,于是,在估计产品的可靠度时,首先需要通过样本对参数λ进行估计。

1.2 矩估计

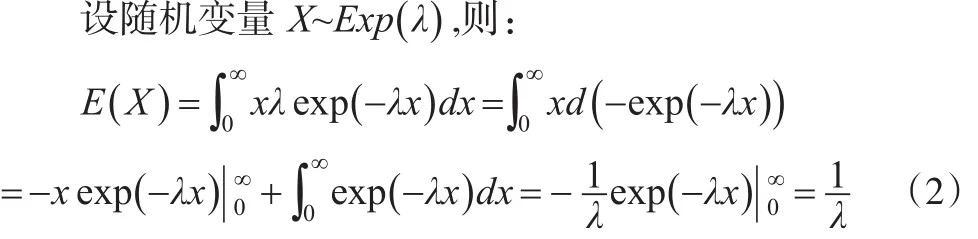
所以有λ=1/EX，故λ的矩估计为：

在指数分布中，有时记θ=1/λ，则θ为指数分布的数学期望。

另外，又因为：

由此可得X方差为：

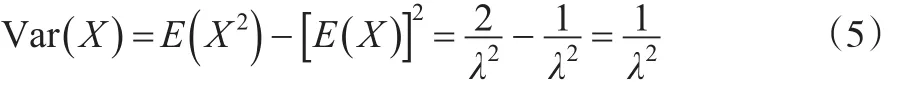
所以，根据替换原理，λ的矩估计也可以取为：

其中s为样本标准差。由此可得到不同的矩估计，这是矩估计的一个缺点。为了计算简便，此时应该选用低阶矩来估计。

例1：由指数分布Exp(3)，产生如下10个来自该分布的样本数据，0.920、0.143、0.1268、0.146、1.136、0.217、0.678、0.022、0.0004、0.0966，可认为是产品某性能指标服从Exp(3)的10个样本，其样本均值=0.349，现要求产品的性能指标不大于1.5时，根据式（3）可计算λ的估计值为=1/=2.865 ，再依据公式（1）可计算其可靠性为=0.9864。

1.3 极大似然估计

对指数总体Exp(λ)设有样本，则其似然函数为：

其对数似然函数为：

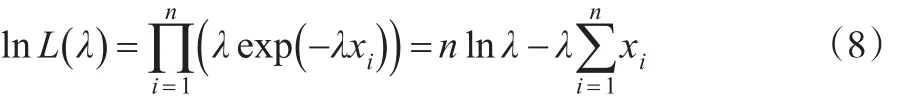
将lnL()λ关于λ求导并令其为0得到似然方程：

解之得：

由于：

于是，是极大值点。

所以，=1/是λ的极大似然估计。这与式(3)的矩估计结果一致。

2 Bayes方法

经典学派方法是根据总体信息和样本信息进行统计推断；而贝叶斯方法与经典学派方法主要不同之处在于：还需利用先验信息进行统计推断。其基本步骤如下：

（1）总体依赖于未知参数θ的概率密度函数为p(x|θ)，其表示θ取某个值时总体的条件概率密度函数。

（2）确定θ的先验分布 π(θ)。

（3）分两步产生样本X=(x1,x2,…,xn)，首先从 π(θ)中产生θ0，然后再从p(x|θ0)中产生X=(x1,x2,…,xn)，由此可得到X的联合条件概率密度函数为：

它包含了总体信息和样本信息。

（4）由于按上述方法得到的θ0还是未知量，所以仍需兼顾其他可能的θ值，即要用π()θ进行综合，这样可得样本X与未知参数θ的联合分布为：

这个联合分布包含了上述三种信息。

（5）将h(X,θ)作如下分解：

其中m(X)是X的边际概率函数：

由此可以得到参数θ的后验分布计算公式：

（6）选取后验分布均值：

或后验分布的其他特征量做估计。但是根据以下定理，一般选取后验分布均值作为参数θ的估计量。

定理1[5]：设损失函数L(θ,a)=(θ-a)2，且Eθ2＜∞则：

为参数θ唯一的Bayes估计。

仍然以指数分布为例，讨论其参数λ的Bayes估计。设X1,X2,…,Xni.i.d.～Exp(λ)。取θ的共轭先验分布为伽玛分布 Γ(b,α)，其中超参数b,α已知，求λ的Bayes估计。

设X=( )X1,X2,…,Xn,则X的密度函数为：

从而λ的似然函数为：

其中∝的含义是：其余因子与λ无关，而λ的共轭先验分布为 Γ(b,α)，即：

则λ的后验分布：

添加正则化常数后，得到：

此后验分布为伽玛分布Γ( )n+b,nx+α。

故由定理1可知，取λ后验期望估计为其Bayes估计：

仍然采用例1的数据，根据以上推导，运用Open BUGS软件采用Gibbs抽样法抽取10000个样本编程对其可靠性进行MCMC模拟可以得到=3.006，其可靠性估计值为R=0.9889。其参数迭代过程及参数分布图如图1和图2所示。

图1 Bayes参数估计迭代图

图2 Bayes方法参数分布图

3 Bootstrap和Bayes Bootstrap方法

Bootstrap方法最早是由斯坦福大学教授Efron于1977年提出的。此方法认为经验分布函数能够较好地拟合总体分布，但在小样本条件下，其拟合效果可能会比较严重，导致过大的估计误差，因而可以考虑通过再抽样来增加样本量。Bayes Bootstrap方法(亦称为随机加权法)，它的基本思想是：通过随机加权来扩充小样本的样本量，以此对参数进行估计。这两种方法都是通过计算机模拟，从小样本中抽取再生样本来获得大样本，由此对未知分布进行模拟。

下面是Bootstrap方法的基本步骤：

（2）从Fn中抽取N组自助样本具体方法为：

①从[0,M](M＞＞n)中产生随机整数η，其必须满足独立性和均匀性的要求。

②令i=η%n，i为n整除η得到的余数。

③从原生样本中以xi作为再抽样本x*，其中xi为与i对应下标的观测样本，则x*可作为所需的随机样本。

（3）计算以下的自助统计量：

（4）用Rn（在给定经验分布Fn的条件下）的分布去模拟Tn的分布。即有，于是可得到N个，由此可求出θ的分布和特征量。

将Rn换成随机加权统计量：

沿用例1的数据，不考虑先验信息的情况下，由于样本量n=10。设Fn是样本X的经验分布函数，=1/是指数分布F参数的估计。则估计误差：

构造并产生N=10000组自助统计量：

图3 Bootstrap方法参数分布图

表1 评估结果比较表

构造并产生N=10000组自助统计量：

由Bayes Bootstrap方法估计参数λ得到其服从的分布如图4所示，其估计值见表1。

图4 Bayes Bootstrap方法参数分布图

4 四种方法的比较

通过表1所列结果，可以看出贝叶斯方法和Bayes Bootstrap方法相对于另外两种方法对可靠性的估计结果更为精确。但是本算例中贝叶斯方法是基于伽玛分布的先验信息情况下进行的统计推断，然而实际的可靠性分析中先验信息不一定容易获得，此时Bayes Bootstrap就体现出了其优势。另外，由图3和图4发现由Bootstrap和Bayes Bootstrap方法估计得到的参数仿真曲线符合伽玛分布概率函数曲线，这与λ的后验分布一致，这也给我们提供了在没有先验信息情况下，如何运用Bayes方法提供了一种思路，即先用Bootstrap和Bayes Bootstrap方法模拟出参数估计的分布概率密度曲线，以此确定先验分布的形式，然后再运用Bayes方法进行估计。因此，在具体分析中，几种方法综合运用能起到更好的估计效果。

5 结束语

本文以指数分布为例对小样本情况下的可靠性参数估计问题进行了对比研究，并通过数值模拟说明了算法的有效性。模拟结果表明，在具有先验信息情况下，Bayes方法和Bayes Bootstrap方法更为适用；并给出了在没有先验信息情况下，Bayes方法和Bayes Bootstrap方法结合使用的思路。但是如何通过改进Bootstrap方法扩充样本容量来提高估计的精度还有待进一步的研究。

[1]Efron B.The Jackknife,the Bootstrap and other Resampling Plans[M].Philadelphia:SIAM,1982.

[2]孙慧玲,胡伟文.小样本条件下参数估计方法比较研究[J].统计与决策,2014,(24).

[3]马智博,朱建士,徐迺新.有关正态分布的小样本可靠性评估[J].核科学与工程,2003,23(4).

[4]曹军海,杜海东,申莹.基于改进Bayes-Bootstrap方法的系统可靠性仿真评估[J].装甲兵工程学院学报,2016,30(1).

[5]陆璇.数理统计基础[M].北京：清华大学出版社,1998.