基于指数威布尔分布的组合统计模型

包振华，张 姝

（辽宁师范大学 数学学院，辽宁 大连 116029）

0 引言

保险损失数据因既包含大量小额损失又包含少量的高额损失，从而具有尖峰厚尾的特点。在保险精算相关文献中，很多学者使用对数正态分布、逆高斯分布、伽马分布及威布尔分布等单一分布对此类数据进行拟合，但对实际损失数据的尾部拟合往往不足。Cooray和Ananda（2005）[1]提出了一类组合统计模型，他们用对数正态分布拟合小额损失而用帕累托分布拟合髙额损失，同时保证对数正态分布和帕累托分布的平滑连接。使用丹麦火灾损失数据拟合实验表明，该组合模型的拟合效果优于单一模型。Scollnik（2007）[2]使用可变权重系数代替文献[1]中组合模型的常系数，提高了组合模型的拟合效果，并提出对数正态-广义帕累托组合模型。Scollnik和Sun（2012）[3]按相同的思路设计了威布尔-帕累托组合模型，并与对数正态-帕累托组合模型进行比较。Bakar等（2015）[4]提出一种新的组合方法，该组合模型依据组合分布的参数调节混合权重系数和阈值，研究了威布尔分布与其他厚尾分布的组合，实证结果显示威布尔-布尔组合模型拟合效果最优。

本文采用文献[4]的方法研究指数威布尔分布与一类转换贝塔分布族的组合统计模型，使用R语言对丹麦火险损失数据进行拟合，并通过似然比检验比较指数威布尔组合模型和相应的威布尔组合模型。

1 指数威布尔分布

指数威布尔分布（以下简记为EW分布）通过在威布尔分布中增加一个形状参数得到，最早由Mudholkar和Srivastava（1993）[5]提出，相关性质可参见文献[6]。设随机变量X服从EW分布，其分布函数为：

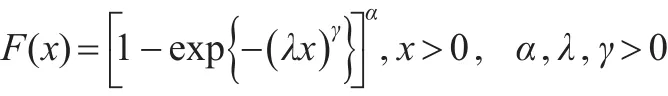
相应的概率密度函数为：

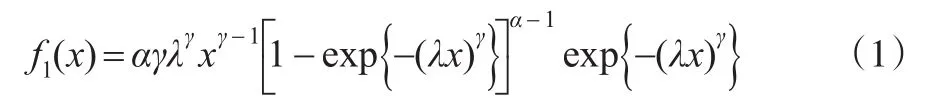
其中α为第一形状参数，γ为第二形状参数，λ为尺度参数。图1和图2分别展示了EW密度函数关于两个形状 参 数α,γ的 变 化 。 当λ=0.5,γ=2时，分 别 取α=0.5,1,2,4，EW分布密度变化如图1所示。EW分布的密度曲线都是单峰的，且当参数α＜1时，概率密度单调递减。保持参数γ,λ不变，随着α的增加，概率密度的峰值右移且变大，密度曲线形态越来越相似。当λ=0.5,α=2时，分别取γ=0.5,1,2,4，EW分布密度变化如图2所示。当γ＜1时，概率密度函数单调递减，且只有尾部形态。保持参数α,λ不变，随着γ的增加，概率密度的峰值越来越大，且尾部越来越薄。

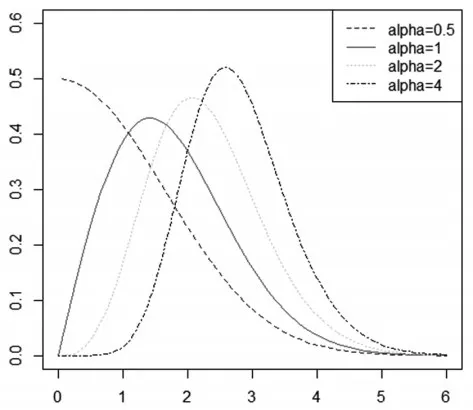
图1 EW分布关于参数α概率密度变化

图2 EW分布关于参数γ概率密度变化

相较于威布尔分布的单调失效率函数，EW分布的失效率函数根据形状参数和尺度参数取值范围的不同而呈现出不同的特征。具体的，当α=γ=1时，失效率函数为一条直线；γ≥1且αγ≥1时，失效率函数单调递增；γ≤1且αγ≤1时，失效率函数单调递减；γ＜1且αγ＜1时，失效率函数为浴盆型；γ＞1且αγ＞1时，失效率函数为反浴盆型。这些独特属性使得EW分布在寿命数据分析方面得到了广泛的应用。

特别地，当α=1时，EW分布退化为经典的威布尔分布；当γ=1时，EW分布退化为广义指数分布（以下简记为EE分布）。EE分布的形态与威布尔和伽马分布相似，相关性质参见文献[7]。

2 指数威布尔组合模型

考虑Bakar等（2015）[4]提出的组合方法，组合模型的密度函数具有如下形式：

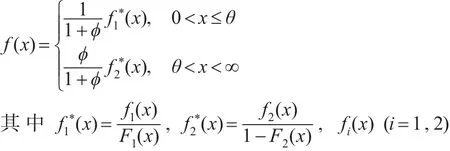
为某个概率密度函数，Fi(x)为相应的累积分布函数。为保证概率密度的连续性，组合模型在阈值θ处满足以下两个条件：

根据约束条件（2），可以给出参数φ的具体表达式：

其中(⋅)=1-Fi(⋅)。根据约束条件（3），参数θ可由式（5）确定：

以下假设f1(x)由式（1）确定，而f2(x)属于转换的贝塔分布族，其密度函数由下式确定：

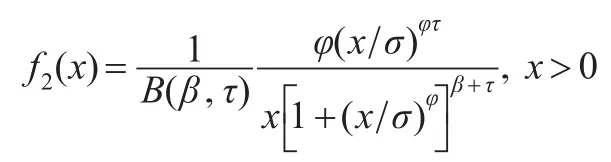
其中β，φ和τ是三个形状参数，σ是尺度参数，且所有参数均大于零，贝塔函数B(⋅)定义为：

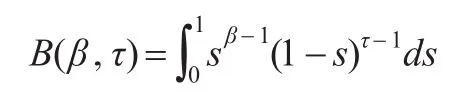
本文将考虑转换的贝塔分布族中如下六种形式的分布，详细介绍参见文献[8]：

（1）当φ=1时，f2(x)退化为广义帕累托分布；

（2）当β=1时，f2(x)退化为逆布尔分布；

（3）当β=1,φ=τ时，f2(x)退化为逆Paralogistic分布；

（4）当φ=1,τ=1时，f2(x)退化为帕累托分布；

（5）当τ=1,φ=β时，f2(x)退化为Paralogistic分布；

（6）当τ=1时，f2(x)退化为布尔分布，具体表达式如下：

本文仅以EW-布尔组合模型为例，即f2(x)由式（6）确定，其他组合模型的构造过程类似。根据式（4），φ的表达式可写成如下形式：

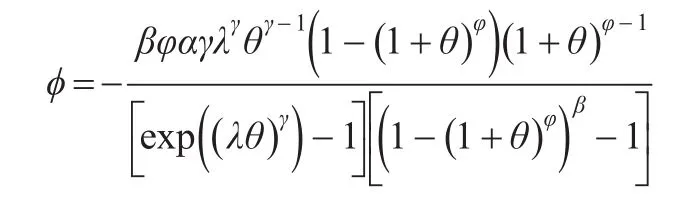
尽管阈值θ没有一个确切的表达式，但它可以根据式（5）求出数值解。经过化简，最终EW-布尔组合模型共由六个未知参数α,γ,λ,β,φ,σ确定。EW分布、布尔分布及EW-布尔组合模型的密度函数如图3所示，其中EW分布参数取为α=4,γ=2,λ=0.5，布尔分布参数为β=1.5,φ=0.5,σ=1。EW-布尔组合模型的密度峰值比EW分布更小，尾部比EW分布更厚，说明EW-布尔组合模型可以更好的拟合低频高额损失数据。

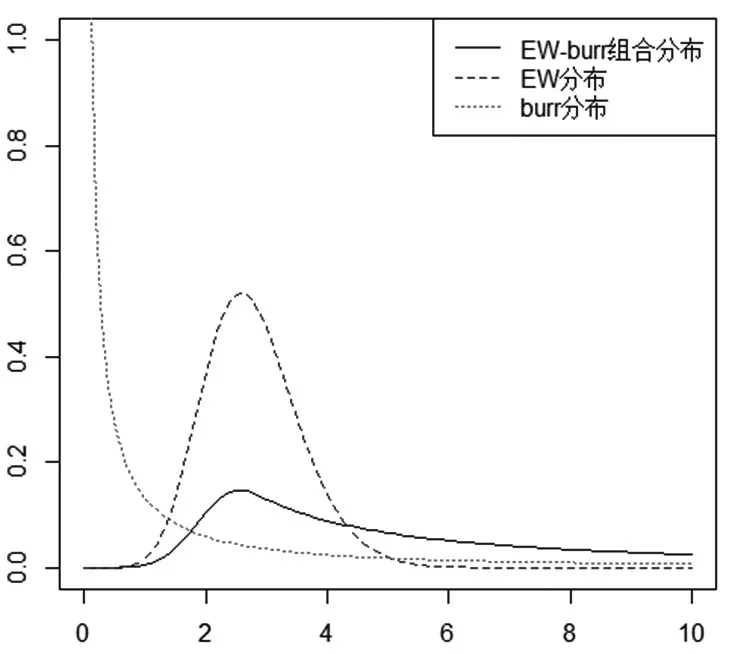
图3 EW-布尔组合模型密度函数图

3 丹麦火灾损失数据的实证分析

本文引用丹麦火灾损失数据进行实证分析。该数据记录了1980—1990年由火灾引起的保险索赔数据，并将数据调整到1985年的物价水平，以排除通货膨胀和价格指数等因素的影响，单位是百万克朗，共2492个数据，其中损失低于1百万克朗的数据有325个。该数据集可在R语言的SMPracticals包中找到。丹麦火险损失数据的相关描述性统计量如表1所示。

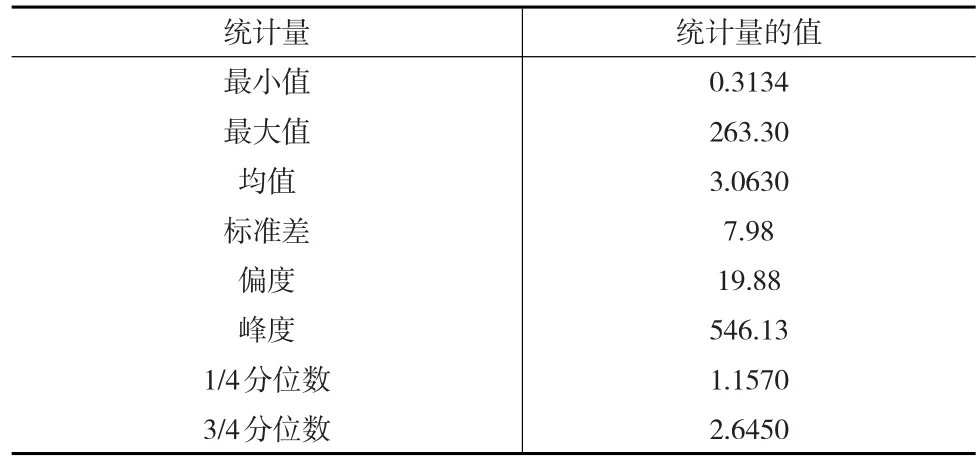
表1 丹麦火灾损失数据描述性统计量

由表1可知，该组数据的峰度为546.13，偏度为19.88，且1/4分位数与3/4分位数离最大值很远，具有明显的正偏性，如图4所示。图5的损失数据直方图显示该组数据在1左右处达到密度峰值，并有很长的右拖尾，说明数据具有明显的尖峰厚尾特征。

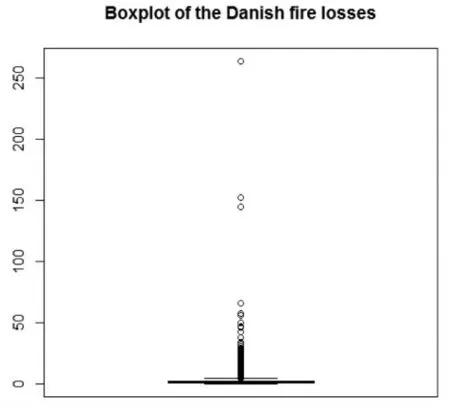
图4 丹麦火险数据箱线图

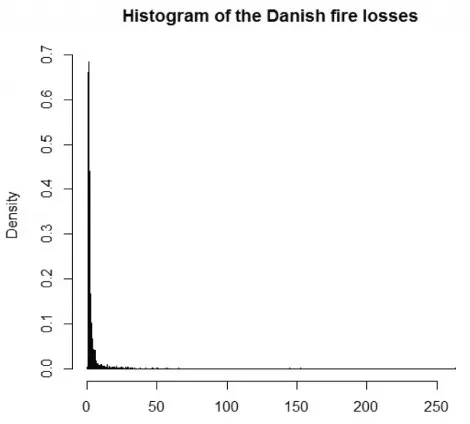
图5 丹麦火险数据柱状图

使用最大似然估计法对组合模型进行参数估计，以NLL、AIC和BIC作为检验标准，并借助R语言实现具体运算。如前所述，本文将考察转换贝塔分布族中的六种分布，包括帕累托分布、广义帕累托分布、布尔分布、逆布尔分布、Paralogistic分布以及逆Paralogistic分布。基于EW组合模型的估计结果如表2所示。

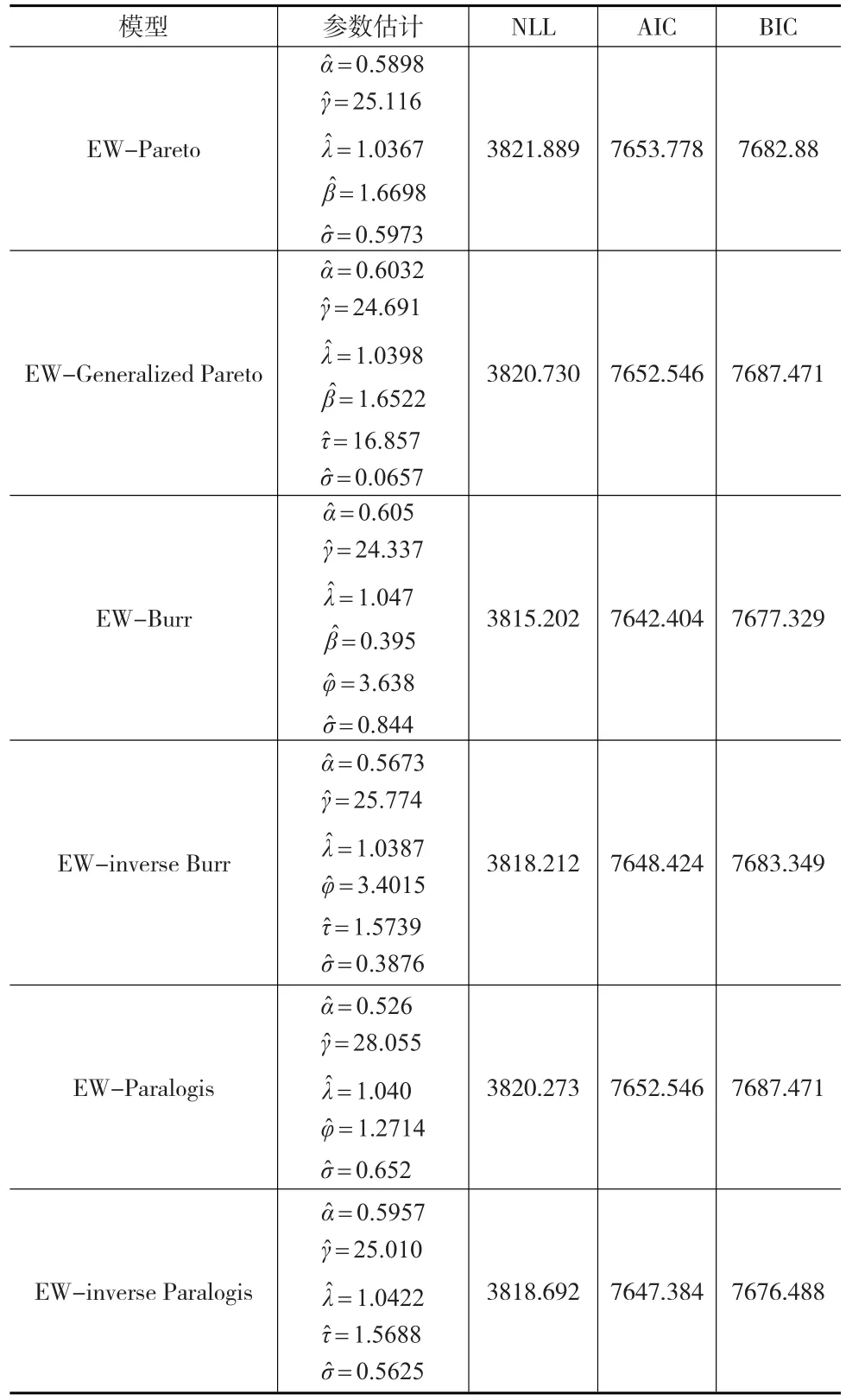
表2 EW组合模型的估计结果

根据表2结果显示，各EW组合模型中参数α,γ,λ的估计值十分相似，说明EW组合模型的拟合差异主要取决于阈值后分布的拟合效果。其中EW-布尔组合模型的NLL和AIC在所有组合模型中最小，意味着在这两个准则下EW-布尔组合模型的拟合效果最好。由于布尔分布比逆Paralogis分布多一个参数，EW-布尔组合模型的BIC比EW-逆Paralogis组合模型大0.841，意味着在BIC准则下EW-逆Paralogis组合模型的拟合效果最好。

由于EW-帕累托组合模型和EW-布尔组合模型是分级的巢式模型，且前者是后者的特例，下面采用似然比检验来判断EW-布尔组合模型拟合效果是否有显著性提高。检验量似然比表达式如下：

其中L(θ0)和L(θ1)分布表示EW-帕累托组合模型和EW-布尔组合模型的最大对数似然值。根据表2可知LR=2[3821.889-3815.202]=13.374，根据Wilks提出的理论，LR近似符合自由度为1的卡方分布，根据卡方检验临界值表，显著性水平为0.001时对应临界值为9.500，说明LR相应p值应小于0.001，且EW-布尔组合模型与EW-帕累托组合模型比显著性提高。

特别地，当EW分布中的形状参数α=1时，EW组合模型即转化为威布尔组合模型，基于威布尔组合模型的估计结果如表3所示。

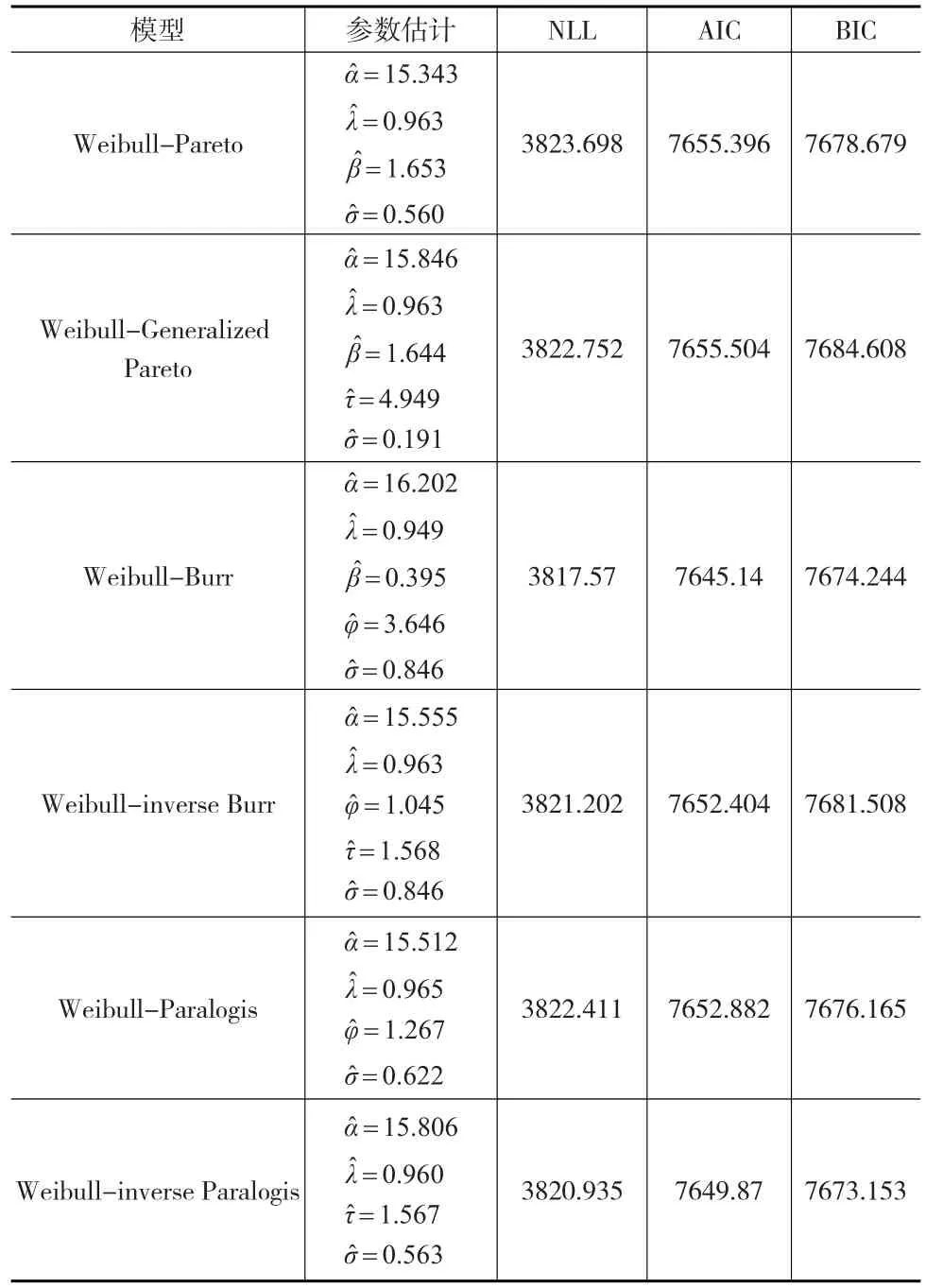
表3 威布尔组合模型的估计结果

根据表3结果显示，威布尔-布尔组合模型的NLL和AIC最小，说明在这两个准则下威布尔-布尔组合模型的拟合效果最优，这个结论与Bakar等(2015)[4]的研究结果一致。与表2结果对比，威布尔组合模型与相应EW组合模型阈值后分布拟合结果相似，说明两种组合模型拟合效果差异主要取决于阈值前的分布拟合效果。

注意到威布尔组合模型是相应EW组合模型的特例，并且根据表2和表3结果可知EW组合模型的NLL值比相应的威布尔组合模型小2至3。以比较EW-布尔组合模型和威布尔-布尔组合模型拟合效果为例，根据式(7)可得LR=2[3817.57-3815.202]=4.736，当自由度为1显著性水平为0.05时，卡方临界值为3.841，说明LR相应p值应小于0.05，EW-布尔组合模型的拟合效果与威布尔-布尔组合模型相比有显著性提高。类似地可知每个EW组合模型相较于威布尔组合模型有显著性提高。

4 结论

保险损失数据往往呈现尖峰厚尾的特点，相比于单一分布，组合模型可以明显提高这类数据的拟合效果。本文基于指数威布尔分布构建了一类组合统计模型，其中阈值之后的分布取自转换的贝塔分布簇，当参数取特殊值时获得六种具体的组合分布。使用R语言对丹麦火险损失数据做拟合分析，给出六种组合模型的参数估计及拟合优度比较，结果表明EW-布尔组合模型在NLL和AIC准则下拟合效果最好。根据似然比检验，EW组合模型拟合效果相较于威布尔组合模型有显著性提高，意味着在尖峰厚尾损失数据建模中，EW组合模型具有较大优势。

[1]Cooray K,Ananda M M A.Modeling Actuarial Data With a Composite Lognormal-Pareto Model[J].Scandinavian Actuarial Journal,2005,(5).

[2]Scollnik D P M.On Composite Lognormal-Pareto Models[J].Scandinavian Actuarial Journal,2007,(1).

[3]Scollnik D P M,Sun C.Modeling With Weibull-Pareto models[J].North American Actuarial Journal,2012,16(2).

[4]Bakar S,Hamzah N A,Maghsoudi S,et al.Modeling Loss Data Using Composite Models[J].Insurance Mathematics and Economics,2015,(61).

[5]Mudholkar G S,Srivastava D K.Exponentiated Weibull Family for Analyzing Bathtub Failure Rate Data[J].IEEE Transactions on Reliability,1993,(42).

[6]Pal M,Ali M M,Woo J.Exponentiated Weibull Distribution[J].Statistica,2006,2(2).

[7]Gupta R D,Kundu D.Exponentiated Exponential Family:an Alternative to Gamma and Weibull[J].Biometrical Journal,2001,43(1).

[8]Klugman S A,Panjer H H,Willmot G E.Loss Models:From Data to Decisions[M].New Jersey:Wiley,2012.