基于Matlab的数字图像离散余弦变换及应用

赵宇杰 石海丽 张妍 高楠 兰州城市学院电子与信息工程学院

1 绪论

随着信息处理技术和计算机技术的飞速发展，数字图像处理技术在各个领域受到了广泛重视并取得了众多成就。语音、图像、数据等多媒体的传输、处理、存储、检索技术成为网络技术的重要组成部分，图像压缩技术尤为重要。离散余弦变换在图像压缩和其他处理中具有计算速度快的优势。

2 数字图像的离散余弦变换及应用

2.1 原理

DFT是数字图像处理中常用变换，离散余弦变换（DCT）是其中的一种特殊情况。傅里叶变换使用无穷区间上的复正弦基函数和信号的内机描述信号中的总体频率分布，或者是将信号向不同频率变量基函数矢量投影。它存在的一个很大问题是参量均是复数，在数据的描述上相当于实数的两倍。DCT的变换核为实数，计算复杂性低、可分离、有快速算法，因此计算速度比DFT 要快得多，被广泛地使用。

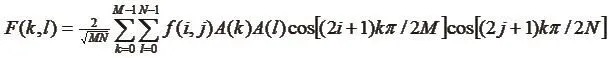
其中，

其中

通常，数字图像的DCT系数的值很接近于0，若忽略这些值，在进行图像重构时不会使图像质量明显下降[2]。在合理近似时，压缩技术应该使用最少的系数，压缩大小取决于系数多少。DCT压缩原理如图1所示，G为输入数字图像，G′为逆变换后的复原图像，U为二维正交变换，U′为二维正交逆变换，A为变换域中的变换系数，A′为量化后的变换系数。

2.2 应用实例

DCT的Matlab实现有两种方法:一种是基于FFT的快速算法，通过工具箱中的dct2函数实现；另一种是DCT变换矩阵法[3]。变换矩阵法常做8行8列或16行16列的DCT变换:首先进行图像分解，然后进行二维DCT，再将DCT系数进行编码和传送，解码时进行逆变换，最后进行图像组合。在此过程中，工具箱中的dctmtx函数能够用来计算变换矩阵。

通过使用Matlab语言中的imread、rgb2gray、dct2函数读取图片信息、进行灰度转换、图像余弦变换系数计算后，按照变换矩阵法，使用dctmtx、mask、blkproc等函数将图像进行压缩的效果如图2所示。

图2 原始图像及其经压缩、解压缩后的效果对比

3 结论

在上述采用DCT进行图像压缩的实例中，去掉了一些允许忽略的高频成分，很好的保留了图像的绝大部分成分，保证了图像重构后失真很少，压缩与解压效果良好。

[1]赵小川，何灏，缪远诚.MATLAB数字图像处理实践[M].北京：机械工业出版社，2013：42-75.

[2]崔春燕，李彩霞.基于DCT变换的数字图像压缩技术及其MATLAB实现[J].现代电子技术，2002，（9）：7-9.

[3] 张汗灵.MATLAB在图像处理中的应用[M].北京：清华大学出版社，2008：81-95.