关于参数的假设检验及其应用

齐莲敏

（襄阳汽车职业技术学院 公共课部， 湖北 襄阳 441021）

在汽车制造、检测、维修、保养、理赔等领域常会碰到参数的假设检验问题，解决这类问题的主要方法是：先对具体问题建立数学模型，提出零假设、备择假设，选取合适的统计量，由统计量的分布以及显著性水平确定否定域、接受域及临界值，然后由样本观察值计算出统计量的观察值，最后根据统计量观察值是否落入否定域来推断零假设是否成立。以下分两个方面来讨论。

一、一个正态总体参数的假设检验

（一）已知总体方差 σ2，检验 H0：μ=μ0

当检验只涉及一个总体时，可能需要对总体的期望μ或总体的方差σ2进行检验，对于这种检验我们要用到以下抽样分布定理。

定理 1.[1]总体服从正态分布N(μ，σ2)，（X1，X2，L，Xn）是容量为n的样本，且Xi（i=1,2,L,n）相互独立，则服从N（0，1）。 （其中为样本均值）

例1.已知某汽车制造厂旧机床加工零件的椭圆度近似服从正态分布，其总体均值为μ0=0.064mm，总体标准差为σ0=0.016mm。现在换一种新机床进行加工，抽取n=100个零件进行检验，得到的椭圆度均值为0.06 mm。问：新机床加工零件的椭圆度均值与以前相比有无显著差异？（α=0.05）

[分析]在这个问题中，机床厂加工零件的椭圆度看成是总体X，由实践和理论知道，总体X服从正态分布 N(μ0，σ20)。

现在换一种新机床进行加工，作为生产者，我们想知道：新机床加工零件的椭圆度均值与以前相比有无显著差异？

为了计算简便，可认为新机床加工零件的方差仍为σ20，此时问题归结为：在方差σ2=σ20已知条件下，检验现在的均值μ与过去的均值μ0相比有无显著差异。

通过以上分析，下面给出解答。

解：第一步，提出假设H0：μ=μ0（=0.064），备择假设：H1：μ≠μ0。

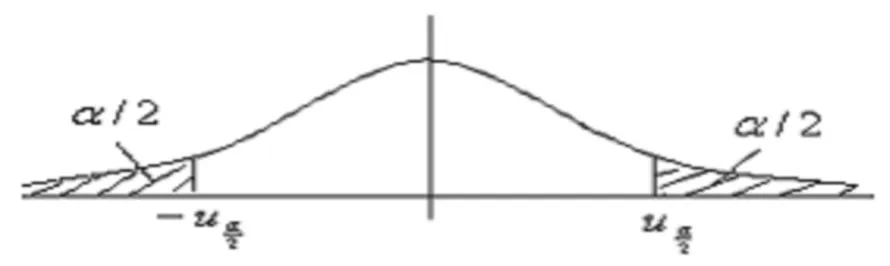
第四步，作出结论：由于u∈U*，所以拒绝H0，即不能认为新机床加工零件的椭圆度均值与以前比没有显著差异，说明存在系统误差，需要对新机床重新进行调试然后再检测。

（二）未知总体方差 σ2，检验 H0：μ=μ0

在工程实际中，总体的方差σ2往往是未知的，可以用样本方差s2来替代，先看下一个定理。

定理 2.[2]设X1，X2，L，Xn（n≥2）相互独立，且都服从N（μ，σ2），则统计量服从自由度为n-1 的t分布，即T～t（n-1）。

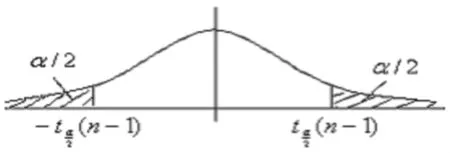
例2.某汽车轮胎制造厂家宣称：在一定的汽车重量和行驶条件下，其生产的轮胎的平均寿命大于40 000 km，现抽取50个轮胎，测得寿命均值为43 000 km，标准差为5 000 km。问：该厂生产的轮胎与其所宣传的标准相符吗？（α=0.01）

[分析]设总体近似服从正态分布。已知总体的均值μ0=40000，样本均值的观察值x=43000，样本标准差的观察值s=5000，要检验样本所代表总体的均值μ是否大于40 000。假设H0：μ≤μ0=40000成立，则；若在一次实验中“小概率事件”发生了，那就应该否定所作出的假设。

解：第一步，提出零假设H0：μ≤μ0，备择假设H1：μ〉μ0。

第四步，作出结论：该厂家生产的轮胎与其所宣传的标准相符。

二、多个总体的参数的假设检验

例3.有三种牌号的轮胎，从中随机抽取6个进行实验，得到轮胎使用寿命的数据如表1。

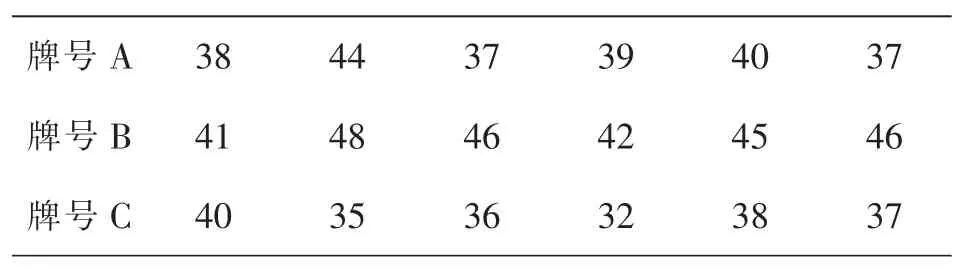
表1 三种牌号轮胎使用寿命调查表（单位：千公里）

问：可以认为这三种牌号的轮胎使用寿命相同吗？ （α=0.05）

[分析]影响轮胎的使用寿命有多种因素，在这个问题中，只考察牌号的影响，是单因素。有三种牌号，即有三种处理，用A1，A2，A3表示。 处理的个数用r表示，则r=3。三种处理所取样本的大小相同，均为n=6。

设在处理Ai下的实验结果Xi是相互独立的正态总体，分别服从N（μi，σ2），i=1，2，3，第i种处理的第j个结果Xij（j=1，2，…，6）是总体Xi的一个简单随机样本，服从N（μi，σ2），即Xij=μi+εij，其中 εij服从N（0，σ2）。

由于不同的处理产生的效应可能不同，把第i种处理产生的效应记作αi，i=1，2，3，那么Xij=u+αi+εij，其中，εij服从N（0，σ2）。

当假设H0为真时，三种处理的均值相同，即μ1=μ2=μ3（等价于a1=a2=a3=0）。

三者的关系式为SST=SSA+SSE。

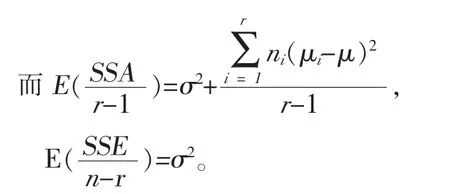
即当假设H0不成立时，有；当假设H0成立时，有。

解：⑴提出零假设H0：μ1=μ2=μ3（等价于 a1=a2=a3=0）；

备择假设H1：μ1，μ2，μ3不完全相同 （等价于a1，a2，a3中至少一个不为 0）。

⑵计算 T1*=235，T2*=268，T3*=219，得到 T**=722；

组内离差平方和SSE=SST-SSA=319.8-208.1=111.7。

⑶列出方差分析表

方差来源 离差平方和 自由度 均方 F值组间方差SSA E=14.06组内方差SSE 208.1 r-1=2 MSA=104.05 MSA MS 111.7 Σni-r=15 MSE=7.4合计 319.8 17

⑷求临界值

显著性水平α=0.05，临界值 Fα（r-1，Σni-r）=F0.05（2,15）=3.68。

最后结论是：不能认为这三种牌号的轮胎使用寿命相同。

[1]李林曙，施光燕.概率论与数理统计[M].北京：中央广播电视大学出版社，2002：8.

[2]刘婉如，徐信之，高尚华.概率与统计（第2版）[M].北京：高等教育出版社，1996.