预制破片侵彻均质装甲钢的极限穿透速度*

赵丽俊,焦志刚,李晓婕,黄晓杰,赵东志,朱小平,唐 辉,王昌富,田 振,喻薪宁

(1.沈阳理工大学装备工程学院,辽宁 沈阳 110159;2.北方华安工业集团有限公司123厂科研一所,黑龙江 齐齐哈尔 161046)

预制破片的穿甲过程，实质上是由炸药装药爆炸产生的爆轰能量驱动预制破片，使其获得较大的初始动能，在距爆心一定距离上以一定的着速和姿态着靶,在冲击动力作用下能够击穿一定厚度的均质装甲目标，在装甲上形成贯穿的孔穴，通常指标要求击穿装甲后预制破片仍需具备一定的杀伤动能，文献[1-9]中均有说明。在预制破片弹威力设计过程中，预制破片的极限穿透速度设计是关键，预制破片的极限穿透速度与其性能(材料、密度、形状和力学性能)、着靶姿态(平均投影面积和投影周长)和靶板性能(材料、厚度和力学性能)等有关，已知预制破片和靶板的性能参数，其极限穿透速度就可以推导出来。本文中，为了研究预制破片的极限穿透速度，利用已知的预制破片参数和靶板参数建立数学模型，通过理论计算和实弹驱动试验对球形、方形和柱形预制破片的极限穿透速度进行研究，由于实弹驱动试验预制破片存在一定的飞散角，试验结果与理论计算结果存在一定的误差，采用弹道枪对3种形状规则预制破片的极限穿透速度进行了复核试验，并给出了计算公式的修正系数，该研究方法在预制破片穿甲威力设计过程中具有实际指导意义。

1 极限穿透速度公式推导

1.1 预制破片飞行方向与靶板法线方向成0°侵靶

进行公式推导之前，先研究公式的特殊情况，假设预制破片垂直靶面穿甲时，被剪切塞块与靶板的分离过程中，塞块与靶板发生相对运动所受阻力主要是靶板材料的抗剪切力，靶板材料的抗剪切屈服极限为τ，并且分布在塞块与靶板的接触面上，于是得到预制破片和塞块的共同运动方程[2-3]：

(1)

式中：m为预制破片的质量，b为装甲靶板厚度，Sb为塞块横截面积，近似等于预制破片着靶平均投影面积，ρb为装甲靶板密度，LY为预制破片着靶时投影周长，τ为装甲靶板的抗剪切屈服极限，x为预制破片穿甲行程。

vdv(m+bSbρb)=-LY(b-x)τdx

(2)

积分得：

(3)

(4)

终止条件x=b时，此时预制破片穿甲后的剩余速度v=0，代入上式得:

(5)

上式即为预制破片飞行方向与靶板法线平行侵靶时预制破片极限穿透速度的近似计算公式，极限穿透速度可定义为穿靶成功时的临界着靶速度。这里需要指出说明，公式推导过程中忽略了预制破片着靶时预制破片和靶板发生的弹、塑性变形消耗的动能，以及预制破片克服摩擦做功消耗的动能及剪切靶板转化为热能对穿甲的影响，所以，理论计算的极限穿透速度比实际测得的极限穿透速度小[5-16]。

1.2 预制破片飞行方向与靶板法线方向成α角侵靶

当预制破片飞行方向与靶板法线方向呈任意角α时，假设预制破片与靶板的作用是刚体与刚体间的碰撞，二者碰撞瞬间不发生弹塑性变形(实际上α太大时预制破片会发生跳飞现象)，则在被剪切塞块与靶板的分离过程中，仅是预制破片穿靶厚度发生变化，使塞块与靶板发生相对运动所受阻力要大，需要克服靶板材料的抗剪切力也要大，靶板材料的抗剪切屈服极限为τ，并且分布在塞块与靶板的接触面上，于是得到预制破片和塞块的共同运动方程：

(6)

式中：α为预制破片飞行方向与靶板法线方向夹角。通过推导，得出预制破片以α角斜侵彻靶板的极限穿透速度近似计算公式为：

(7)

1.3 着靶平均投影面积和投影周长

以棱长为a的立方体预制破片为例，研究其在任意着靶姿态下的平均投影面积和投影周长，从3种预制破片着靶姿态对其进行研究，预制破片着靶姿态见图1。

1.3.1预制破片任意一个面的法线方向与靶板法线方向平行

当预制破片的一个面与靶板作用时，预制破片的平均投影面积S1=a2，着靶时的投影周长C1=4a，几何关系见图2(a)。

1.3.2预制破片任一棱长与靶板法线方向垂直

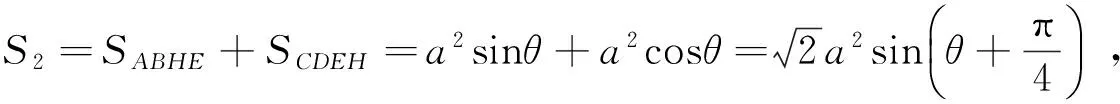
1.3.3预制破片任一顶点与靶板法线方向成任意角

2 实例计算

采用上述推导公式对图3所示的3种形状预制破片的极限穿靶速度进行理论计算，分别计算垂直侵靶和斜侵彻侵靶(取θ=30°)的极限穿靶速度。预制破片和均质装甲靶板参数见表1，已知预制破片几何尺寸、预制破片质量，均质装甲钢板厚度、均质装甲钢板抗剪切屈服极限τ。

形状破片尺寸m/gh/mmτy/MPa方形a=7.3mm7.00101700圆柱形R=4.0mmH=7.0mm6.33101700球形R=2.5mm4.70101700

2.1 极限穿透速度计算

在预制破片垂直侵靶和斜侵彻侵靶(通常轻型装甲的倾角为30°，这里以30°为例进行计算)条件下，根据式(5)对3种形状规则预制破片的极限穿透速度进行了计算。预制破片垂直侵靶和斜侵靶的极限穿透速度计算结果见表2，其中S为破片平均投影面积，L为破片投影周长。

表2 预制破片垂直侵靶和斜侵靶时理论计算数据Table 2 Calculation data of target’s vertical and oblique penetration by prefabricated fragment

2.2 计算结果分析

计算结果表明，预制破片的极限穿透速度与其着靶姿态、侵靶角度和靶板的性能参数有关，当预制破片的着靶投影面积最大、投影周长最大时其极限穿透速度最大；预制破片极限穿透速度随其斜侵彻倾角的变化而发生变化。当今轻型装甲车辆的倾斜装甲倾角约为30°[7]，在实战中多数预制破片不是垂直侵彻靶板，所以，在设计预制破片的极限穿透速度时，应考虑预制破片的着靶投影面积、投影周长及其飞行方向与靶板法线方向夹角，穿甲威力设计要留有一定的裕度。

3 验证试验

为验证3种形状规则预制破片的极限穿透速度，对3种形状预制破片分别在距爆心15、11和8 m处对10 mm均质装甲钢板的穿透能力进行实弹驱动静爆威力试验，见图4。采用通靶、断靶结合的方式对3种形状预制破片的着靶速度和靶后剩余速度进行测试[8]，试验数据见表3。

表3 预制破片侵靶试验结果Table 3 Test results of prefabricated fragment penetrating target

试验表明，方形预制破片着速为1 044.7 m/s，柱形预制破片着速为1 071.4 m/s，球形预制破片着速为918.0 m/s，3种形状预制破片均穿透10 mm的均质装甲钢板，方形预制破片的剩余能量为69.3 J、柱形预制破片的剩余能量为145.8 J、球形预制破片的剩余能量为37.0 J，剩余均低于对人员的有效杀伤准则，此时的着速最接近其极限穿透速度。预制破片理论计算的极限穿透速度(垂直侵靶)与实弹驱动试验测得的极限穿透速度相差较大，这是由于在试验中，预制破片实际上是以一定的飞散角着靶的，而计算时是以绝热和刚体碰撞作为假设条件的[9]，实弹驱动试验测得的极限穿透速度与理论计算得到的极限穿透速度(斜侵彻)基本吻合，也说明了这一点。

4 修正系数

由于实弹驱动试验预制破片存在一定的飞散角，并不是垂直侵靶，为了验证理论计算和实弹驱动试验测得数据的相对误差，3种形状预制破片的模拟弹头用塑料弹托固定，如图5所示。

采用弹道枪进行模拟复核试验[8]，枪击试验预制破片同样采用方形、球形和柱形。采用14.5 mm弹道枪(见图6)，靶板为10 mm厚均质装甲钢板(见图7)，通过选配14.5 mm机枪发射装药试验，选出每种预制破片的临界穿透药量。临界穿透定义为破片完全嵌入靶板，即将穿透的状态(图8)，再增加适量发射药，直至预制破片完全穿透靶板为止，此时的药量为预制破片极限穿透速度的药量，采用该药量每种预制破片射击3发，平均着靶速度即为该形状预制破片的极限穿透速度，试验结果见表4。

表4 弹道枪试验结果Table 4 Test results of ballistic gun

将弹道枪模拟复核试验测得的着靶速度与表2中垂直侵彻理论计算得到的极限穿透速度进行对比发现，方形预制破片的极限穿透速度理论值比试验值小约32.6%，柱形预制破片的极限穿透速度理论值比试验值小约32.0%，球形预制破片的极限穿透速度理论值比试验值小约25.3%；与斜侵彻理论计算(以30°角侵彻)结果相比：方形预制破片的极限穿透速度理论值比试验值小约3.55%，柱形预制破片的极限穿透速度理论值比试验值小约3.27%，球形预制破片的极限穿透速度理论值比试验值小约2.90%。与实弹驱动静爆威力试验结果相比：方形预制破片的极限穿透速度偏小约5.6%，柱形预制破片的极限穿透速度偏小约5.4%，球形预制破片的极限穿透速度偏小约4.7%。

理论计算与试验有一定差距，这是由于在公式推导过程中忽略了预制破片和靶板发生弹塑性变形、破片因克服摩擦和靶板发生剪切破坏等因素对着靶动能消耗的影响和破片斜侵彻等造成，且试验预制破片穿甲剪切面积比理论计算穿甲剪切面积略大，从而导致极限穿透速度理论计算结果比实际试验结果较小，因此须引入修正系数k对计算公式进行修正，通过对试验结果和理论计算结果进行数据对比和分析处理，得出修正系数k(修正系数k只对侵彻均质装甲钢有推广意义,对于其他材料的靶体不适用)。由式(7)拟合给出形状规则预制破片极限穿透速度的修正计算公式：

(8)

通过对理论计算、实弹驱动试验结果和弹道枪复核试验结果的对比分析，考虑到极限穿透速度设计应有一定的裕度，初步给出方形、柱形和球形3种形状规则预制破片极限穿透速度理论计算的修正系数，方形破片的k值约为1.48，圆柱形破片的k值约为1.47，球形破片的k值约为1.34，从修正系数k还可以看出预制破片的阻力系数越小，计算结果与试验结果越接近。

5 结 论

(1)通过对方形、柱形、球形预制破片垂直侵彻均质装甲钢理论计算公式进行推导，进一步得出形状规则预制破片斜侵彻均质装甲钢极限穿透速度理论计算公式，通过计算，分别对方形、柱形、球形预制破片垂直侵彻和 斜侵彻10 mm厚均质装甲钢的极限穿透速度进行理论计算，验证计算公式的实用性。

(2)采用实弹驱动和弹道枪复核验证试验的方法，分别对3种形状预制破片的着速和极限穿透速度进行了试验测定，通过实测结果与理论计算结果对比分析，得出弹道枪复核验证试验测得极限穿透速度与不同着靶条件下的极限穿透速度理论计算结果的误差，与弹道枪复核试验结果相比，较垂直侵彻理论计算结果偏大；较斜侵彻理论计算结果偏小；较实弹驱动试验结果偏小。

(3)通过对实例计算结果、实弹驱动试验结果和弹道枪复核试验结果进行对比分析，对计算公式给出了修正系数k，方形破片的修正系数最大，柱形破片的修正系数次之，球形破片的修正系数最小，这与不同形状预制破片的阻力系数相关，k值越小，理论计算结果越接近试验值，修正的计算公式能够指导工程实践中形状规则预制破片侵彻均质装甲钢的穿甲威力设计。

[1] 石志杰,姜春兰.不同形状预制破片的速度衰减特性及极限贯穿速度分析[J].弹箭与制导学报,2004,24(1):312-314.

SHI Zhijie, JIANG Chunlan. Different shapes of preformed fragment velocity attenuation characteristics and throughout limit velocity analysis[J]. Journal of Projectiles Rockets, Missiles and Guidance, 2004,24(1):312-314.

[2] 贾光辉,孙学清,裴思行.极限穿透速度与靶板材料动态屈服强度[J].弹道学报,1998,10(4):46-49.

JIA Xiaohui, SUN Xueqing, PEI Sixing. Limit penetration velocity and dynamic target plate material yield strength[J]. Journal of Ballistics, 1998,10(4):46-49.

[3] 高润芳,韩峰,马小青,等.几种钨合金破片垂直侵彻装甲钢板极限穿透速度研究[J].弹箭与制导学报,2005,25(4):57-59.

GAO Runfang, HAN Feng, MA Xiaoqing, et al. Several kinds of tungsten alloy fragment vertical penetration armor penetration speed limit[J]. Journal of Projectiles Rockets, Missiles and Guidance, 2005,25(4):57-59.

[4] 尹放林,王明洋,钱七虎.弹体垂直侵彻深度工程计算模型[J].爆炸与冲击,1997,17(4):333-339.

YIN Fanglin, WANG Mingyang, QIAN Qihu. Projectile vertical penetration depth engineering calculation model[J]. Explosion and Shock Waves, 1997,17(4):333-339.

[5] 印立魁,蒋建伟,门建兵,等.立方体预制破片战斗部破片初速计算模型[J].兵工学报,2014,35(12):1967-1971.

YIN Likui, JIANG Jianwei, MEN Jianbing, et al. Cube prefabricated fragment warhead fragment velocity calculation model[J]. Acta Armamentarii, 2014,35(12):1967-1971.

[6] 彭军,袁宝慧,程淑杰,等.立方体破片对钢靶的穿甲威力研究[J].科学技术与工程,2014,11(29):7092-7096.

PENG Jun, YUAN Baohui, CHENG Shujie, etal. Cube pieces of steel target power research[J]. Science, Technology and Engineering, 2014,11(29):7092-7096.

[7] 冯美玲,陈智刚,徐元生,等.钨合金破片斜侵彻铝板极限速度研究[J].机电技术,2015.36(1):17-19.

FENG Meiling, CHEN Zhigang, XU Yuansheng, etal. Tungsten alloy fragment oblique penetration aluminum plate speed limit[J]. Mechanical and Electrical Technology, 2015,36(1):17-19.

[8] 翁佩英,任国民,于骐.弹药靶场试验[M].北京:兵器工业出版社,1995.

[9] 黄长强,朱鹤松.球形破片对靶板极限穿透速度公式的建立[J].弹箭与制导学报,1993(2):58-61.

HUANG Changqiang, ZHU Hesong. The spherical fragment to the establishment of a target board through speed limit formula[J]. Journal of Pojectiles rockets, Missiles and Guidance, 1993(2):58-61.

[10] 王超,安振涛,甑建伟.长方体破片对金属薄板的极限穿透速度研究[J].弹箭与制导学报,2012,32(3):92-95.

WANG Chao, AN Zhentao, ZENG Jianwei. Cuboid broken piece of research on the limit of sheet metal penetration rate[J]. Journal of Projectiles Rockets, Missiles and Guidance, 2012,32(3):92-95.

[11] BACKMAN M E, GOLDSMITH W. The mechanics of pengtration of projectiles into targets[J]. International Journal Engineering Science, 1978,16(12):1-99.

[12] ZUKAS J A. Impact dynamics[M]. New York: New York Wiley Inter Science, 1982.

[13] CHARLES E, ANDERSON J, DAVID L, et al. Long-rod penetration, target resistance,and hypervelocity impact[J]. International Journal of Impact Engineering, 1993,14(1/2/3/4):1-12.

[14] 康爱花,陈智刚,付建平.球形破片侵彻高强度装甲钢的弹道极限速度计算[J].中北大学学报(自然科学版), 2015,36(6):647-651.

KANG Aihua, CHEN Zhigang, FU Jianping. Penetration armor high strength steel spherical fragment ballistic limit velocity calculation[J]. Journal of Zhongbei University (Natural Science Edition), 2015,36(6):647-651.

[15] CARLEONE J.Tactical missile warheads[M]. Washington: The Americal Institute of Aeronautics and Astronautics, 1993:462-464.

[16] CHARRON Y J. Estimation of velocity distribution of fragmenting warheads using a modified gurney method: ADA074759[R]. Air Force Institute of Technology, Ohio, 1979:40-42.