计算CHNO和CHNOAl炸药爆速的一种新方法*

杨慕天，郑 波

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

炸药的爆速是衡量炸药爆轰性能的重要标志量。目前，常用的爆速计算方法大致上可分为两大类：第一类是通过热力学状态方程计算爆速，例如BKW方法[1]和VLW方法[2]等；第二类是通过对实验数据关联得到经验公式对爆速进行计算，例如Kamlet方法[3]、Urizar方法和Stine方法[4]等。前者需要求解状态方程，计算量较大，在实际应用中受到一定的限制；后者在计算上相对较为简单，但Kamlet方法和Stine方法均需要生成热数据，对于新型炸药的应用受到了限制，而Urizar方法计算某些非理想炸药的计算值与实验值偏差过大。

本文中基于“理想混合炸药”模型[5]的概念，发展了一种计算混合炸药爆速的半理论半经验新方法，并对CHNO类和CHNOAl炸药进行计算，该方法物理意义明确，计算结果可靠。

1 计算方法

1.1 新方法描述

根据化学热力学原理[6]，混合物的性质与混合物中各组分的性质及混合物的组成有关，因此将混合炸药作为固体混合物，并将混合炸药的爆速D作为固体混合物一种特殊的性质考虑，据此用数学方法进行处理。

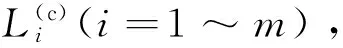
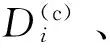
(1)

设混合炸药的爆速为D，有T=L/D，则式(1)转化成:

(2)

(3)

式中:wi为第i种纯组分的质量分数，把式(3)带入式(2)得:

(4)

1.1.1CHNO类混合炸药

若混合炸药是由单质炸药组合而成，没有添加剂，则式(4)简化成:

(5)

从式(5)中可知，只需确定了D(a)，就可以得到混合炸药的爆速与混合炸药组成及纯组分炸药的爆速之间的定量关系，由此可预算混合炸药的爆速。当ε(a)=0即装药密度ρ0达到最大理论密度时，得到最大理论爆速:

(6)

考虑到冲击波在空气中的衰减规律，当ε(a)趋近于零时，有D(a)趋近于最大理论爆速Dm，初步得到D(a)与Dm的关系式为：

D(a)=Dmexp(αε(a))

(7)

式中:α为待定系数(α<0)。通过对大量实测混合炸药爆速的研究，当取α=-5.05时，可得到比较好的结果。因此，混合炸药爆速的计算可采取如下公式:

(8)

1.1.2CHNO类单质炸药

对于不同装药密度的单质炸药，可看作是1.1.1节中的特殊情况，即混合炸药中只有一种单质炸药，没有添加剂，则单质炸药的爆速计算公式为:

(9)

1.1.3含铝炸药

对于含铝炸药，其添加剂为铝，则式(4)简化为:

(10)

铝的最大爆速由ε(Al)=0和ε(a)=0时得到。假设ε(Al)和ε(a)均为零，可得：

(11)

(12)

则含铝炸药的爆速计算公式为:

(13)

1.2 Urizar公式

文献[7]中提到计算混合炸药爆速的计算的Urizar公式：

式中：D、ρ0分别表示混合炸药的爆速、装药密度；εi、Di、ρi、wi分别表示第i种纯组分炸药的体积分数、特征爆速、最大理论密度、质量分数；铝和空气的特征爆速分别为6 850和1 500 m/s。

1.3 Kamlet公式

文献[7]中提到根据BKW状态方程的RUBY编码计算结果，归纳了计算CHNO等炸药爆速的半经验公式：

(14)

式中：Φ表示炸药的特征值，ρ0表示炸药的装药密度。

对于由炸药与炸药组成的混合炸药，Φ值采取近似计算方法[8]：

(15)

式中:wi、Φi分别表示第i种纯组分炸药的质量分数、特征值。将式(15)代入式(14)中，即可得到混合炸药爆速的计算公式。

2 计算结果与讨论

根据新方法推导出的爆速计算公式，分别对装药密度大于85%最大理论密度的26种CHNO类混合炸药、13种CHNO类单质炸药和25种含铝炸药进行爆速D的计算，并与实验得到的爆速值[5,7,9-12]以及利用Kamlet公式的计算值和Urizar计算值的结果列于表1～3，为便于观察。通过数据处理把这三种不同计算方法的总体精度列于表4。新方法计算含铝炸药爆速时，忽略粘结剂对爆速的影响。

由表2可知，将不同装药密度的单质炸药作为特殊的混合炸药来处理，其计算结果依然具有较为可观的精度。

由表3可知，由于wax所占质量分数很小，故忽略了它的影响，使得主体炸药质量分数增大，从而导致计算结果偏大，但相对误差仍然小于3%，满足精度要求，其特征爆速以后再做讨论。Urizar方法在计算非理想度较高的含铝炸药爆速时，误差明显增大，而新方法则能够避免。

表4结果表明，对于CHNO类炸药和含铝炸药，新方法的计算值与实验值的平均相对误差和最大相对误差均低于Urizar方法和Kamlet方法，64种炸药的平均相对误差为0.01%，并且相对误差分布稳定，相关系数为0.961 5，说明新方法计算值更加逼近实验值。

表1 CHNO类混合炸药爆速的实验与计算对比Table 1 Comparison between experimental and calculated data of mixed CHNO explosives detonation velocity

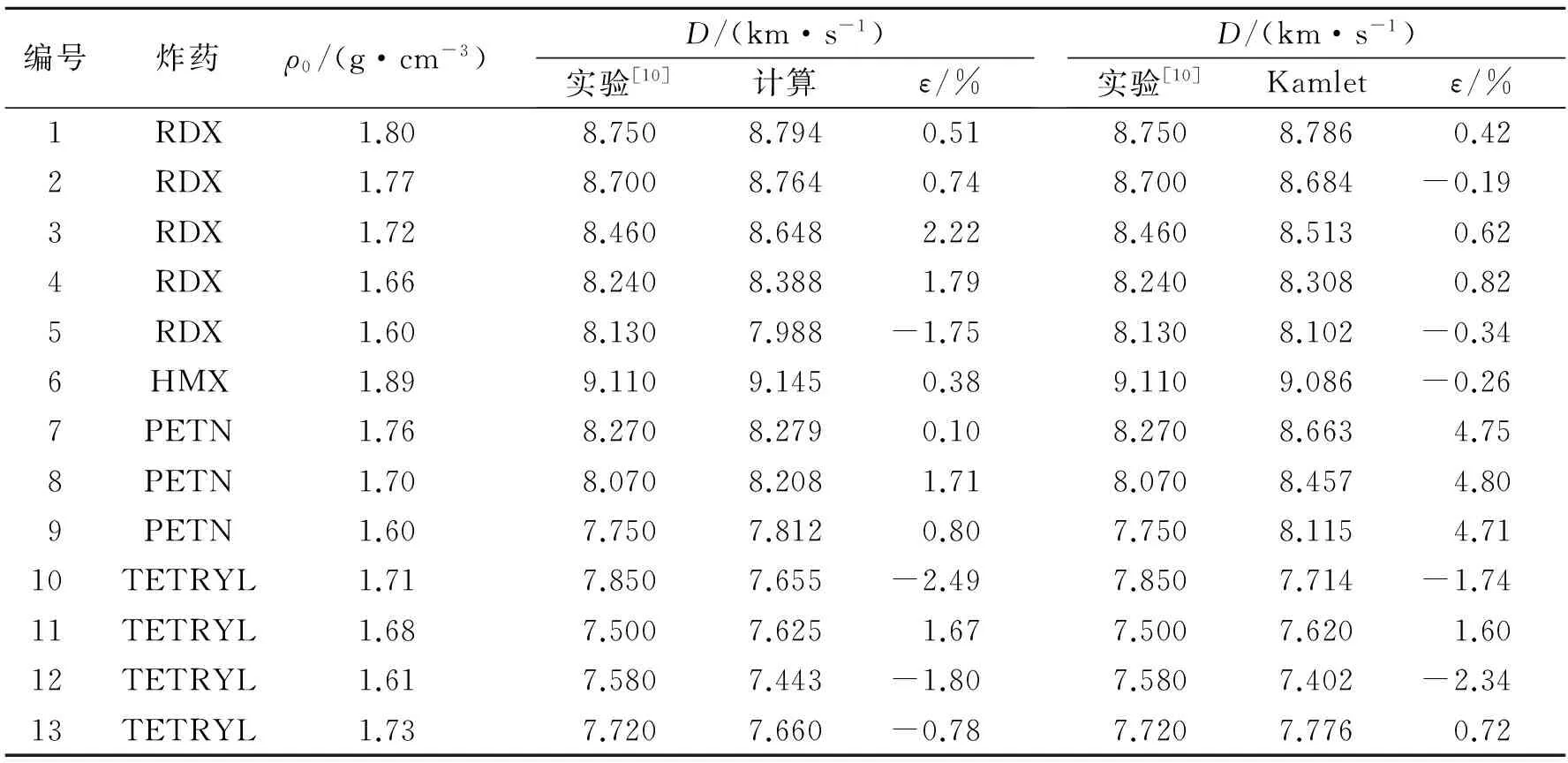
表2 CHNO类单质炸药爆速的实验与计算对比Table 2 Comparison between experimental and calculated data of pure CHNO explosives detonation velocity

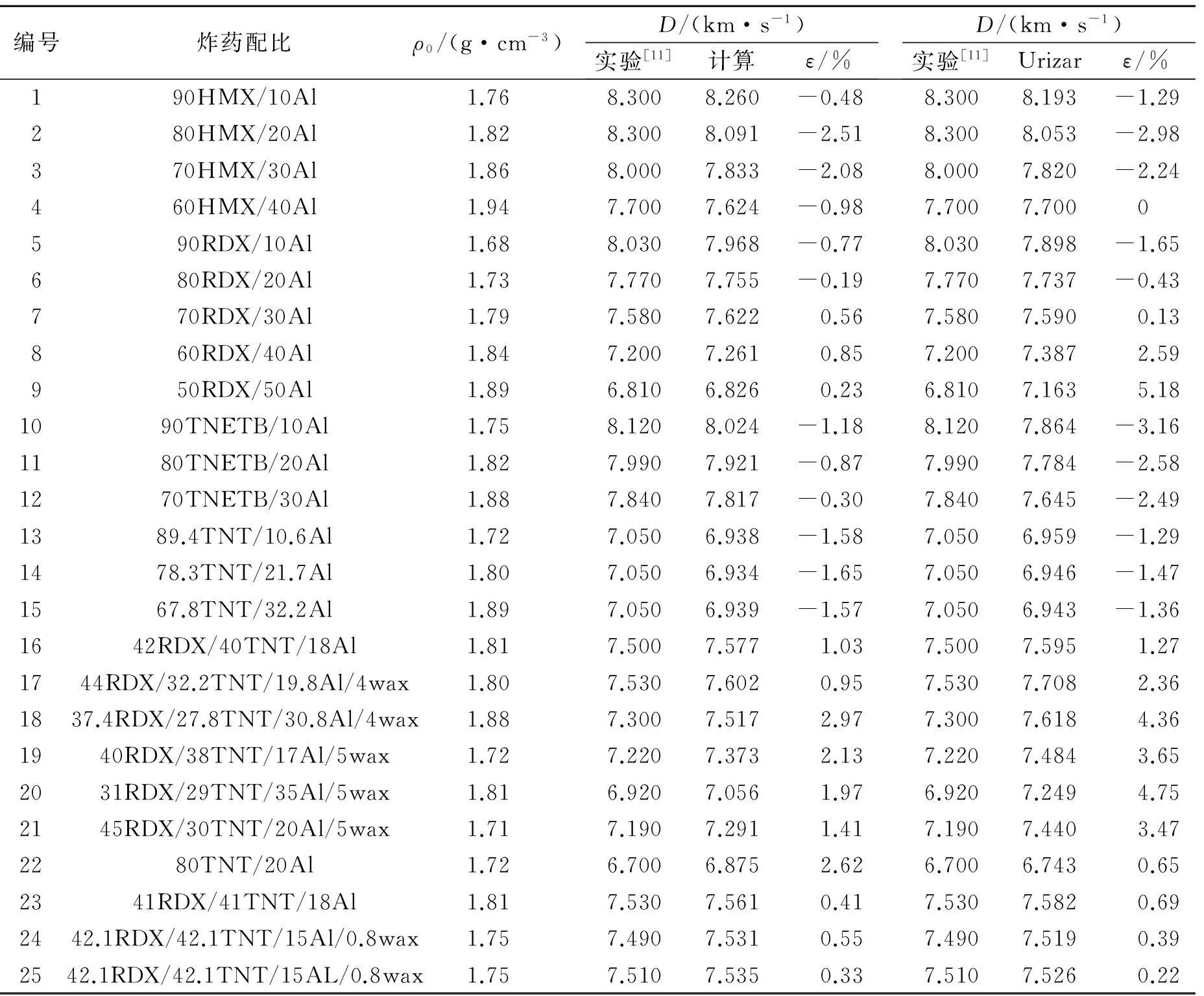
表3 含铝炸药爆速的实验与计算对比Table 3 Comparison between experimental and calculated data of aluminized explosives detonation velocity

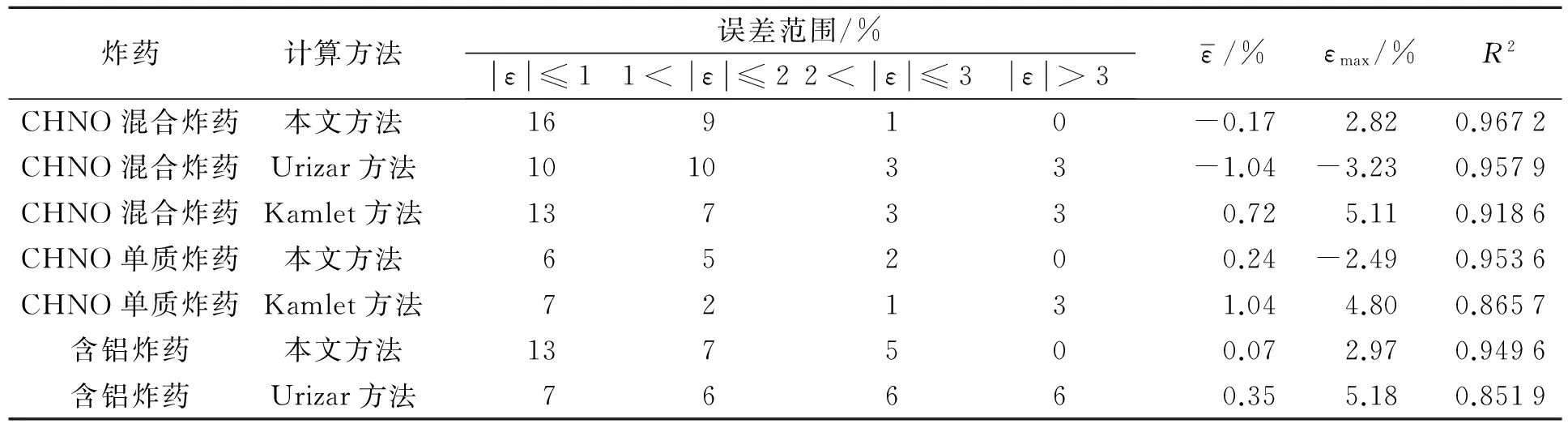
表4 不同计算方法的精度对比Table 4 Comparison of calculated accuracy between different methods

3 结 论

本文中建立了计算混合炸药爆速的模型，对CHNO和CHNOAl炸药给出了计算爆速的具体公式，有利于理解混合炸药各组分对爆速的贡献，其结果优于现有的Urizar方法和Kamlet方法，此方法对混合炸药爆速计算具有良好的适用性。因此，应用新方法可以合理的预测新型混合炸药的爆速，对探索新型炸药有一定的指导意义。

[1] MADER C L. Numerical modeling of explosives and propellants[M]. Boca Raton: CRC Press, 2008:31-63.

[2] 陈朗,龙新平,冯长根,等.含铝炸药爆轰[M].北京:国防工业出版社,2004:30-42.

[3] KAMIET M J, JACOBS S J. Chemistry of detonations Ⅰ: A simple method for calculating detonation properties of C-H-N-O explosives[J]. Journal of Chemical Physics, 1968, 48(1): 23-25.

[4] 李金山.计算含能材料爆速的一种新方法[J].火炸药学报,1994,17(3):28-32.

LI Jinshan. A new method for calculating the detonation velocity of energetic materials[J]. Explosives and Propellants,1994,17(3):28-32.

[5] 王克强,孙献忠.理想混合炸药模型的提出及其应用[J].火炸药学报,2002,25(1):51-53.

WANG Keqiang, SUN Xianzhong. An ideal composite explosive model proposed and its application[J]. Explosives and Propellants, 2002,25(1):51-53.

[6] 桑德勒 S I.化学与工程热力学[M].吴志高,译.北京:化学工业出版社,1985:173-460.

[7] 孙业斌,惠君明,曹欣茂.军用混合炸药[M].北京:兵器工业出版社,1995:82-83.

[8] 孙业斌.爆炸作用与装药设计[M].北京:国防工业出版社,1987.

[9] 郭金波.理想混合炸药爆速的计算[J].洛阳师范学院学报,2003,22(2):41-44.

GUO Jinbo. The calculation of the detonation velocity of an ideal composite explosive[J]. Journal of Luoyang Teachers College, 2003,22(2):41-44.

[10] KESHAVARZ M H. A simple approach for determining detonation velocity of high explosive at any loading density[J]. Journal of Hazardous Materials, 2005,121(1/2/3):31-36.

[11] KESHAVARZ M H. Predicting maximum attainable detonation velocity of CHNOF and aluminized explosives[J]. Propellants Explosives Pyrotechnics, 2012,37(4):489-497.

[12] 韩早,王伯良.混合炸药爆速预报的新方法[J].爆炸与冲击,2014,34(4):421-426.

HAN Zao, WANG Boliang. The new method for predicting detonation velocity of composite explosive[J]. Explosion and Shock Waves, 2014,34(4):421-426.