椭圆截面弹体侵彻砂浆靶规律分析*

王文杰，张先锋，邓佳杰，郑应民，刘 闯

(南京理工大学机械工程学院,江苏 南京 210094)

传统侵彻弹截面形状一般为圆形，随着电磁炮、机载滑翔武器和天基动能武器等新型发射平台的发展，非旋转对称的异型侵彻体开始发展起来。近些年，国内外学者广泛开展了非旋转对称异型截面侵彻体的飞行阻力特性和侵彻性能研究[1-3]。非旋转对称异型侵彻体主要有两类：一类是在弹体头部或者圆柱部刻槽，以期改变侵彻体的侵彻阻力特性：庞春旭等[4-5]设计了一种头部刻槽弹体，通过侵彻铝靶实验验证了头部刻槽弹体的侵彻深度明显优于常规卵形弹体；陈小伟等[6]、梁斌等[7]、张欣欣等[8]开展了圆柱部刻槽弹体侵彻混凝土靶实验，结果表明弹体圆柱部刻槽在提高弹道稳定性的同时，对侵彻深度的提高也有一定贡献。范少博等[9]开展了弹身刻直槽和螺旋槽弹体的侵彻仿真及实验研究，结果表明弹体外表面刻槽可提高侵彻深度且螺旋刻槽弹体具有更好的侵彻能力；第二类非旋转对称异型侵彻体是弹身采用异型结构：杜忠华等[10-11]、高光发等[12]分别开展了三角形、矩形和圆形截面的长杆弹垂直侵彻半无限金属靶的实验和数值模拟研究，结果表明在一定速度范围内异型杆的侵彻威力大于等截面积的圆形截面杆；Bless等[13-14]通过对异型截面杆和圆截面杆的侵彻能力研究对比发现异形截面杆的侵彻能力受限于其侵彻速度，随速度增加异形截面杆相对圆截面杆的侵彻能力先增加后减小至与圆截面杆相同。目前关于异型结构侵彻体侵彻性能的研究尚属于初步探索阶段，相关的数值模拟和理论研究欠缺，同时针对异型结构侵彻体侵彻混凝土靶的实验现象的描述和所研究的异型侵彻体的种类还相对较少，为此异型侵彻体的研究仍需开展相关理论模型及相关实验来丰富实验数据库。

椭圆截面弹体是非旋转对称异型侵彻体的典型结构，因其装填比大，飞行过程中有较高的升力和纵向稳定性等优点一直被航空航天领域广泛研究，但关于椭圆截面弹体侵彻性能却少有人关注。本文中以椭圆截面弹体侵彻行为为研究对象，以动态球形空腔膨胀理论阻力函数为基础，建立椭圆截面弹体侵彻砂浆靶过程理论模型。设计2种截面尺寸的椭圆截面弹体，开展弹体侵彻砂浆靶实验研究，获得不同截面尺寸的椭圆截面弹体侵彻砂浆靶实验结果，验证了理论模型的可靠性，给出椭圆截面弹体头部阻力特性变化规律，并与普通圆截面弹体侵彻特性进行了对比，给出了椭圆截面弹体设计方法。

1 椭圆截面弹体侵彻理论模型

弹体垂直侵彻靶体过程中所受阻力可分为弹体头部侵彻阻力及弹体侧壁动态摩擦粘滞阻力2个部分。弹体着靶速度较低时，侵彻过程中圆柱段侧壁摩擦较小[15]且侵彻后弹体质量损失不明显，故本文中模型假设弹体刚性且仅考虑弹体头部侵彻阻力。参考Forrestal等[16-18]、Chen等[19]的工作，采用球形空腔膨胀理论拟合得到的靶体阻力函数来分析椭圆截面弹体侵彻靶体过程所受的阻力，继而预测椭圆截面弹体侵彻性能。

1.1 椭圆截面弹体头部形状表达式

对传统圆截面弹体和椭圆截面弹体头部的描述如图1所示。

图1(a)为平面坐标系下传统圆截面弹体头部形状函数示意图，r为弹体半径，R为弹体头部曲率半径，l为弹体头部长度，z为瞬时侵彻深度，R′(z)为侵彻深度为z时弹体横截面半径，侵彻深度为z时存在如下关系：

(1)

(2)

图1(b)是圆截面弹体向椭圆截面弹体过渡示意图。式(2)中，分别将圆截面弹体的x方向半径和y方向半径增大a倍和b倍即得到椭圆截面弹体头部表面方程：

(3)

图1(b)中，取弹头表面一面积微元ds，设微元的外法线方向与弹体的轴线夹角为θ，则：

(4)

由式(4)可知，对于传统圆截面弹体(a=b=1)，θ值只与侵彻深度z有关，同一横截面即侵彻深度z不变时，θ值固定不变，而对于椭圆截面弹体，θ值不仅与侵彻深度z有关，同一横截面上θ值还与长短轴放大倍数a和b相关。

1.2 椭圆截面弹体侵彻受力模型

弹体侵彻过程可分为扩孔/开坑和稳定侵彻2个阶段，在稳定侵彻阶段，弹头表面微元所受法线方向的侵彻阻力σn由静态项Scfc和与速度有关的动态项共同组成[16]：

(5)

式中:fc和ρt分别是靶体无围压强度和初始密度，Sc为量纲一的材料常数，vn为与弹头表面微元的法向速度，vn=vcosθ，v为弹体瞬时侵彻速度。如图1(b)所示，弹体垂直侵彻过程中，弹头表面微元受力可分解为垂直于微元的法向力dFn和沿微元所在母线的切线方向的摩擦力dFτ，已知作用在弹头的法向和切向应力分布，将分布应力向弹轴方向合成，就可求得弹体轴向侵彻阻力Fz。弹体表面局部微元ds所受法向和切向应力在弹轴方向上的合力为：

dFz=dFncosθ+dFτsinθ=σn(cosθ+μsinθ)ds

(6)

式中:μ为弹靶间滑动摩擦因数，侵彻深度对μ的取值很敏感[16]，实际侵彻过程中，μ的大小应与侵彻速度、弹体及靶体的材料性能有关，本文中取μ=0.01[20]。将dFz在整个弹头外表面积分，即可得到弹体在稳定侵彻阶段所受轴向合阻力：

(7)

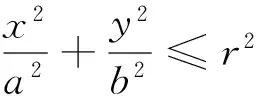
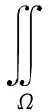
(8)

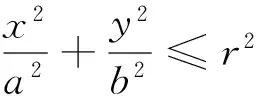
(9)

将式(9)代入式(8)即可得到坐标变换后Fz表达式，将Fz展开可化成静态项和与速度有关的动态项两部分之和：

Fz=A+Bv2

(10)

式中:

其中：c=R-r为定值。

1.3 椭圆截面弹体侵深计算模型

弹体侵彻过程可分为扩孔/开坑和稳定侵彻2个阶段，由牛顿第二定律知：

(11)

式中:m为弹体质量，k为开坑阶段阻力系数。开坑阶段侵彻阻力随开坑深度线性增加，开坑深度近似为弹体半径r的4倍[17]。对于椭圆截面弹体，r即为与其等截面积的圆截面弹体的半径。基于式(10)～(11)，利用初始边界条件v=v0、z=0和终了边界条件v=0，就可求得侵彻深度z：

(12)

式中:v1为开坑区结束时弹体的速度。

2 椭圆截面弹体侵彻模型的实验验证

在理论模型推导的基础上，基于30 mm弹道炮发射平台，设计了2种椭圆截面弹体T1、T2及圆截面弹体L1。其中椭圆截面弹体T1和圆截面弹体L1距离弹尖相同高度处的横截面面积相等，用来研究横截面形状对弹体侵彻性能的影响；2种椭圆截面弹体T1、T2距离弹尖相同高度处的横截面长轴长度相等，短轴不等，用来研究横截面尺寸对椭圆截面弹体侵彻性能影响。实验主要通过通过观察靶体开坑形状、开坑深度、侵彻深度、隧道区形状以及弹体的破坏形式等来研究椭圆截面弹体侵彻性能。

2.1 实验准备

图2为3种弹体横截面尺寸示意图，3种弹体横截面尺寸大小关系为ST2>ST1=SL1。每种实验弹各3发，所有弹体总长均为L=180 mm，弹头长度均为l=58.1 mm。实验弹体由弹身、底推及弹托组成，弹身材料为30CrMnSi2A高强度合金钢，密度为7.85 g/cm3，热处理后硬度为40～45 RHC；底推材料为铝，通过螺纹和弹身连接，密度2.71 g/cm3，直径与炮管直径相同，主要起到发射过程中的闭气作用；弹托材料为尼龙，其外直径和炮管直径相同，主要为了保证弹体在膛内运动的稳定性。所有弹体通过改变内部开孔深度和开孔直径的大小来保证质量相等及弹体质心处于弹体中部，图3所示为3种弹体实物图以及全备弹照片。

由于实验弹尺寸较小，为了避免混凝土靶的局部不均匀性对侵深造成影响，实验中采用不含粗骨料的砂浆靶，图4所示为实验所用的∅1 000 mm×1 000 mm圆柱体砂浆靶，其中靶体细骨料为石英石中粗砂，平均粒度不大于1 mm，水泥、砂和水按1∶1∶0.35质量配比。靶体外围用3 mm厚钢板箍紧，靶直径与弹径之比大于30，可以忽略侵彻过程中靶体边界效应的影响。图5所示为实验现场布置示意图，以30 mm滑膛炮作为加速平台开展弹体次口径正侵彻实验，靶体放在靶架上，靶面中心与炮膛中心在同一直线，用六通道测试仪测量弹体着靶速度，为保证最终测速准确性和着靶姿态为正侵，用高速录像记录弹体飞行过程和着靶姿态。

浇筑靶体时加工了3个边长150 mm的立方体抗压试块，如图6所示，靶体和试样块的浇筑和养护均按照标准规范执行。试块经称重及MTS试验机静态力学性能测试，得到的应力位移曲线如图7所示。实验用砂浆靶密度为2.15 g/cm3，平均无侧限抗压强度fc=40 MPa。

2.2 实验结果

图8所示为高速摄像记录的部分实验弹体着靶瞬间照片，根据高速摄像图片以及实验靶孔观测可知，各实验弹的攻角较小，着靶姿态较理想。

表1给出了实验数据及与理论模型计算所得侵深结果的对比,表中，dmax、dmin、h、γ分别表示最大开坑直径，最小开坑直径，开坑深度和弹道偏转角。其中圆截面弹体 L1-1由于装药过多，速度过高穿透靶体。由表1可知，实验结果与理论计算相对误差ε均小于7%,模型预估与实验结果吻合较好。

表1 实验数据与理论模型结果对比Table 1 Comparison between experimental and theoretical data

图9分别给出了2种截面弹体侵彻后的靶体端面破坏情况和剖靶后观察到的侵彻弹道。椭圆截面弹体对靶体的破坏与传统圆截面弹体相似，也由开坑区和隧道区构成。2种靶体正面都具有典型的高速撞击表面漏斗开坑形状，形成了相对于弹着点基本对称的弹坑区和分布均匀的径向裂纹，裂纹一直延伸到靶体边界。不同之处在于：(1)相同速度下，椭圆截面弹体的平均开坑直径大于卵形弹体，T2弹体开坑直径最大，卵形弹体开坑直径最小；(2)椭圆截面弹体的隧道区弹洞形状呈椭圆形。此外，通过剖靶观察到的隧道区可以看出，弹体侵彻过程中弹道平直，因此认为本次试验弹体为正侵彻。

图10所示为弹体侵靶后的回收照片。从图中可以看出，侵彻过程中弹靶间的相互磨蚀导致弹体表面有显著的沿弹轴向分布的擦痕，弹靶界面压力越大，擦痕越明显。观察发现椭圆截面弹体横截面长轴端点附近区域的擦痕比短轴端点附近区域擦痕明显，表明椭圆截面弹体长轴端点附近与靶体介质的挤压摩擦作用更加强烈。经过测量，弹体的长度损失均小于2%，因此可忽略侵彻过程中的头部侵蚀作用，近似认为实验弹为刚性弹。

3 椭圆截面弹体侵彻混凝土计算结果及讨论

通过对回收弹体观测及靶体解剖分析，认为椭圆截面弹体的侵彻时，椭圆截面弹体横截面长轴端点附近区域受力最大，短轴端点附近区域受力最小，沿着同一横截面从长轴端点到短轴端点过程中，受力逐渐减小。针对上述分析，分为3个部分具体讨论影响椭圆截面弹体侵深的因素。

3.1 等截面积的椭圆截面弹体和圆截面弹体侵彻规律对比

由前述稳定侵彻阶段椭圆截面弹体所受阻力表达式，其中当a≠b时，该模型为椭圆截面弹体阻力计算表达式；当a=1/b≠1时，该模型为与圆截面弹体等截面积的椭圆截面弹体阻力表达式，此时在侵彻速度相等时，2种弹体具有相同的断面比动能；而当a=b=1时，即弹体长短轴参数未作改变时，此时式(10)即为传统圆截面弹体在稳定侵彻阶段所受阻力。

取L1弹体a=b=1，T1弹体a=1/b=1.25。为深入研究弹体横截面形状对其所受阻力的影响，按图11中，取2种弹体距弹尖相同高度处的某一横截面，计算该横截面上各点受力情况。因为4个象限所受阻力对称，这里只比较第一象限2种弹体所受阻力。由于圆截面弹体是轴对称的，所以在同一横截面上其受力为一定值，而椭圆截面弹体由于形状差异，同一横截面上在从长轴端点到短轴端点的圆弧上，其受力呈现正弦曲线形式，结果如图12所示。把(0,π/2)区间上2种弹体所受阻力相加，总阻力相差不大，故两者实验侵深没有明显差别。

3.2 不同横截面尺寸的椭圆截面弹体侵彻规律对比

图13～14给出了相同质量(460 g)和弹长的3种椭圆截面弹体在相同着靶速度(750 m/s)下侵彻40 MPa砂浆靶的理论侵深时间和加速度时间关系曲线。3种椭圆截面弹体T2、T1、T0长轴长度相等，均为30 mm，短轴长度分别是24、19.2和15 mm。观察发现，由于T0弹体横截面面积最小，侵彻相同深度时所压碎、排开的混凝土体积最少，弹体动能损失最小，所以在相同速度下侵彻时，T0弹体侵彻过程加速度更小，侵彻时间更长，最终侵彻深度更大。而T2弹体由于横截面积最大，故侵彻过程加速度最大，侵彻深度最小。

3.3 弹头形状不同的椭圆截面弹体侵彻规律对比

为了研究椭圆截面弹体头部形状对其侵彻性能的影响规律，分别计算质量(460 g)、总弹长、弹头长均相等，弹头形状为如图15所示的卵形T1、椭球形TQ1和锥形Z1的3种椭圆截面弹体在相同着靶速度(750 m/s)下侵彻40 MPa砂浆靶的侵深时间和加速度时间关系。在距离3种弹体弹尖相同高度处取一横截面，椭球形弹头横截面积最大，锥形弹头横截面面积最小。

图16～17给出了相同质量(460 g)和弹长的3种椭圆截面弹体在相同着靶速度(750 m/s)下侵彻40 MPa砂浆靶的理论侵深时间和加速度时间关系曲线。由于椭球形弹头横截面面积最大，速度相等时断面比动能最小，故其侵深最小，侵彻过程加速度最大，侵彻时间最短，锥形头部和卵形头部横截面面积相差不大，故侵深和加速度也比较接近。

4 结 论

建立椭圆截面弹体侵彻阻力模型，并针对传统圆截面弹体和2种不同横截面尺寸的椭圆截面弹体开展了砂浆靶侵彻实验，通过对弹体和靶体的变形和破坏进行分析对比发现：(1) 侵彻过程中椭圆截面弹体横截面长轴端点附近区域受力更大，因此长轴端点附近区域弹体磨蚀更明显；(2)横截面面积是影响椭圆截面弹体侵彻性能的重要因素，横截面面积小的断面比动能大，从而侵深更大。从计算与实验数据对比可以看出，理论计算模型基本是合理的，对椭圆弹体的侵彻深度预测较为准确，然而本文所试验的靶体对象为不含粗骨料的水泥砂浆靶，对于真正意义上的混凝土侵彻时2种弹形是否存在差异，还需要进一步的试验验证。

[1] 荣光,孙瑞胜,薛晓中,等.两种非圆截面弹芯的侵彻性能研究[J].兵工学报,2009,30(4):385-388.

RONG Guang, SUN Ruisheng, XUE Xiaozhong, et al. Penetration performance study on two kinds of non-circular cross-sectional projectiles[J]. Acta Armamentarii, 2009,30(4):385-388.

[2] 朱坤,杨振声.椭圆截面弹身大攻角纵向气动特性的工程计算[J].北京航空航天大学学报,1991,17(4):45-50.

ZHU Kun, YANG Zhensheng. Prediction of longitudinal aerodynamic characteris for elliptical cross-section bodies at high angles of attack[J]. Journal of Beijing University of Aeronautics and Astronautics, 1991,17(4):45-50.

[3] GARON K, FAMINU O. Aeroballistic range tests of missile configurations with non-circular cross-sections and aeroprediction comparison results[C]∥The 41st AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, United States, 2003.

[4] 庞春旭,何勇,沈晓军,等.刻槽弹体旋转侵彻混凝土效应实验研究[J].兵工学报,2015,36(1):47-52.

PANG Chunxu, He Yong, SHEN Xiaojun, et al. Experimental investigation on penetration of grooved projectiles into concrete targets[J]. Acta Armamentarii, 2015,36,(1):47-52.

[5] 庞春旭,何勇,沈晓军,等.刻槽弹体旋转侵彻铝靶实验与数值模拟[J].弹道学报,2015,27(1):70-75.

PANG Chunxu, HE Yong, SHEN Xiaojun, et al. Experimental investigation and numerical simulation on grooved projectile rotationally penetrating into aluminum target[J]. Journal of Ballistics, 2015,27(1):70-75.

[6] 陈小伟,梁斌,姬永强,等.高侵彻能力的先进钻地弹的次口径实验研究[C]∥全国工程结构安全防护学术会议.洛阳,2007:1-6.

[7] 梁斌,陈小伟,姬永强,等.先进钻地弹概念弹的次口径高速深侵彻实验研究[J].爆炸与冲击,2008,28(1):1-9.

LIANG Bin, CHEN Xiaowei, JI Yongqiang, et al. Experimental study on deep penetration of reduced-scale advanced earth penetrating weapon[J]. Explosion and Shock Waves, 2008,28(1):1-9.

[8] 张欣欣,武海军,黄风雷,等.刻槽弹侵彻混凝土受力模型研究[J].爆炸与冲击,2016,36(1):75-80.

ZHANG Xinxin, WU Haijun, HUANG Fenglei, et al. Mechanical model of the grooved-tapered projectile penetrating concrete targets[J]. Explosion and Shock Waves, 2016,36(1):75-80.

[9] 范少博,陈智刚,侯秀成,等.旋进侵彻弹丸数值模拟与实验研究[J].弹舰与制导学报,2013,33(1):81-83.

FAN Shaobo, CHEN Zhigang, HOU Xiucheng, et al. Numerical simulations and experimental study on novel rotating penetrating projectile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013,33(1):81-83.

[10] 杜忠华,朱建生,王贤治,等.异型侵彻体垂直侵彻半无限靶板的分析模型[J].兵工学报,2009,30(4):403-407.

DU Zhonghua, ZHU Jiansheng, WANG Xianzhi, et al. Analytical model on non-circular penetrator impacting semi-infinite target perpendicularly[J]. Acta Armamentarii, 2009,30(4):403-407.

[11] 杜忠华,曾国强,余春祥,等.异型侵彻体垂直侵彻半无限靶板实验研究[J].弹道学报,2008,20(1):19-21.

DU Zhonghua, ZENG Guoqiang, YU Chunxiang, et al. Experimental research of novel penetrator vertically penetrating semi-infinite target.[J]. Journal of Ballistics, 2008,20(1):19-21.

[12] 高光发,李永池,刘卫国,等.长杆弹截面形状对垂直侵彻深度的影响[J].兵器材料科学与工程,2011,34(3):5-8.

GAO Guangfa, LI Yongchi, LIU Weiguo, et al. Influence of the cross-section shapes of long rod projectile on the vertical penetration depth[J]. Ordnance Material Science and Engineering, 2011,34(3):81-83.

[13] BLESS S J, LITTLEFIELD D L, ANDERSON C E, et al. The penetration of non-circular cross-section penetrators[C]∥Proceedings of the 15th International Symposium on Ballistics. Jerusalem, Israel, 1995:21-24.

[14] BLESS S J. Penetration mechanics of non-circular rods[C]∥Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter, 1996,370:1119-1122.

[15] 闪雨,武海军,黄风雷,等.弹体侵彻混凝土侧壁摩擦阻力研究[J].北京理工大学学报,2012,32(1):12-17.

SHAN Yu, WU Haijun, HUANG Fenglei, et al. Study on the behavior of projectile shank friction penetrating into concrete.[J]. Transactions of Beijing Institution of Technology, 2012,32(1):12-17.

[16] FORRESTAL M J, OKAJIMA K, LUK V K. Penetration of 6061-T651 aluminum targets with rigid long rods[J]. Journal of Applied Mechanics, 1988,55(4):755-760.

[17] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994,15(4):395-405.

[18] FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[19] CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics[J]. International Journal of Impact Engineering, 2002,27(6):619-637.

[20] 柴传国,皮爱国,武海军,等.卵形弹体侵彻混凝土开坑区侵彻阻力计算[J].爆炸与冲击,2014,34(5):630-635.

CHAI Chuanguo, PI Aiguo, WU Haijun, et al. A calculation of penetration resistance during cratering for ogive-nose projectile into concrete[J]. Explosion and Shock Waves, 2014,34(5):630-635.