爆炸载荷作用下具有可折叠芯层夹芯梁的动态响应*

张培文，李世强,2,3，王志华,3，赵隆茂,3

(1.太原理工大学力学学院,山西 太原 030024;2.湖南大学汽车车身先进设计制造国家重点实验室,湖南 长沙 410082;3.太原理工大学 材料强度与结构冲击山西省重点实验室,山西 太原 030024)

多孔金属是一类新颖的功能/结构一体化超轻材料，具有优异的物理、热、力学和光电性能，在航空航天、车辆、国防工程中有广泛的应用。由轻质多孔金属作为芯层所组成的夹芯结构，由于其芯层能够产生较大的塑性变形，因此在冲击/爆炸等强动载荷作用下具有优异的能量吸收特性[1]。迄今为止，方孔蜂窝一般都是采用装配的方式按照Russell等[2]提出的生产方法进行生产的，即：在较厚的纸板或者其他材料的板材上开一半宽度的槽，然后再将这些开槽的板材进行装备进而形成方孔蜂窝。Liu等[3]对不同拓扑微结构蜂窝的面内动态冲压行为进行了研究，结果发现当应力超过峰值后，整体呈现从连续的弹性变形到塑性屈曲的平台阶段。McShane等[4]对由不锈钢面板和方孔蜂窝芯层组成的固支夹芯板的动态响应进行了分析，发现夹芯板与等质量实体板相比，具有更优的抗冲击性能；而且方孔蜂窝芯层比点阵材料芯层较优。所有这些研究均局限在芯层为直边方孔蜂窝的面内外压缩，而关于芯层为曲边方孔蜂窝的面内、外压缩在现有文献中鲜有报道；且关于方孔蜂窝胞元初始曲率等几何参数对夹芯结构动态响应影响的研究也尚未见报道。目前，由于折纸艺术具有较广的潜在工程应用，已经引起了科学和工程界的关注。而从一张扁平纸张通过折叠形成三维结构的折纸艺术所提出的Tachi-miura样式[5]，能够通过改变初始折叠角度而形成不同曲边方孔蜂窝胞元，并且通过合理的几何设计能够达到较一些传统蜂窝更优异的力学性能，如负泊松比效应。可折叠的折纸结构已经在空间太阳能电池帆板上进行了应用[6-8]。为了实现折纸结构的优异的力学性能，通常将某些折叠样式的单胞按照一定的规则进行组合[9-10]。针对不同材料和几何参数对折纸结构压缩响应的影响已有较多学者进行了分析[11-14]。Wachinger等[15]对由芳纶纸组成的可折叠夹芯结构进行了高速冲击测试。研究发现：选择合适的夹层和芯层形状能够较好地提高夹芯结构的冲击破坏抗性。但是关于具有可折叠芯层夹芯结构在爆炸载荷作用下的力学响应鲜有报道，因此对爆炸载荷作用下具有可折叠芯层夹芯结构的动态响应进行研究是很有必要的。

本文中，基于目前研究最广泛的刚性折纸(Tachi-origami)样式，通过改变其初始折叠角度构建4种不同的蜂窝胞元，并且通过排列分布将其组成夹芯梁。采用商用有限元软件Abaqus/explicit对准静态载荷和爆炸载荷作用下可折叠芯层及具有可折叠芯层夹芯梁的力学响应进行研究，分析可折叠芯层的泊松比变化规律以及由其组成夹芯梁的背板挠度和能量吸收机理；并与等质量的实体梁进行对比，以期为后续研究提供参考。

1 有限元模型

Tachi-origami折痕样式如图1所示，采用其中1个折叠单元进行几何构建并建立如图2所示的折叠单管模型。采用商用有限元软件Abaqus将折叠单管在3个正交方向上进行多次叠加建立夹芯梁折叠芯层的有限元模型，如图3所示。通过改变初始折叠角α，构建4种不同的蜂窝胞元，并且通过排列分布将其组成4种不同形状的折叠芯层，折叠芯层OC-1、OC-2、OC-3、OC-4分别对应于由初始折角α=45°,60°,75°,90°，将折叠胞元所构成折叠单管进行叠加组合并置于上、下面板之间形成夹芯梁，具体参数如表1所示。在其正上方150 mm处施加爆炸载荷，如图4所示。

表1 不同蜂窝胞元夹芯梁的几何参数Table 1 Geometry parameters of different honeycomb core cells

在有限元模型建立过程中，面板和折叠芯层均采用2 mm的有限元网格进行网格划分，并采用缩减积分单元(S4R)对其截面属性进行描述。其中面板厚度tf=1 mm，芯层厚度tc=0.05 mm。对材料采用弹塑性模型进行描述，其材料密度ρ=7 800 kg/m3，弹性模量E=200 GPa，泊松比ν=0.3。应变和应变率硬化采用了Johnson-Cook模型：

(1)

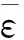
(2)

2 模拟结果与讨论

2.1 单轴压缩下的准静态分析

图5给出了变形前后的Von Mises应力分布云图，从图中可以看到：可折叠芯层的横截面(高度、宽度及长度)都发生了明显变化，在沿着z轴方向施加准静态单轴面外压缩载荷时，变形前后在y方向上产生了较大的膨胀变形，而在x方向上却发生了相对较小的收缩变形。

2.1.1泊松比的变化趋势

本文中将面外泊松比νzx和νzy采用x、y轴名义应变εx、εy与z轴名义应变εz的比值来定义。轴向名义应变采用3个方向的长度变化值与初始长度值的比值进行计算。拉伸应变定义为正值，压缩应变定义为负值。图6给出了3种模型的面外泊松比(νzx和νzy)变化规律。从图中可以看到：3种芯层的泊松比νzx一直都是负值且随着初始折角的增大而减小；但泊松比νzy一直都是正值且随着初始折角的增大而增大。3种可折叠芯层的泊松比变化过程是完全不同的，芯层OC-1的泊松比νzx表现为从-0.537逐渐增大到一个稳定值-0.521，泊松比νzy从1.623 逐渐减小到一个稳定值1.569；芯层OC-2的泊松比νzx首先是减小然后再逐渐增大到一个固定值，泊松比νzy逐渐减小到一个稳定值；芯层OC-3的泊松比νzx表现出与OC-2相同的趋势先减小然后逐渐增大到一个固定值，泊松比νzy却与OC-2的趋势不同，表现为先增加然后逐渐减小到一个稳定值。值得注意的是：泊松比较明显的变化基本上是在单轴压缩应变εz=0.1之前完成的。从图5模拟结果中提取相应的应变时程曲线，并采用泊松比的定义公式进行相应的计算，得到如图6(c)所示的结果。发现该种可折叠芯层在准静态载荷作用下表现出一定的负泊松比效应(膨胀效应)且应力集中现象主要表现在相邻面的交接处，即塑性弯矩最大处。

2.1.2应力应变关系

将接触力与折叠芯层的原始截面积之比定义为名义应力，将试件在沿着加载方向的变形量与试件的原始长度之比定义为名义应变。从而通过计算就能够得到准静态下的名义应力应变曲线，如图7所示。从图中可以看到：3种曲线都包含1个线弹性段、1个明显的屈服点以及1个应变强化段。初始屈服点和应变硬化模量随初始折角的增大逐渐增大。主要的原因是随着初始折角的增大，可折叠芯层的曲率逐渐减小，因此使得折叠芯层产生屈曲就需要更高的应力水平。

2.2 爆炸载荷下的动态响应

2.2.1模型验证

为了验证有限元算法及材料本构模型的可靠性，采用与文献[17]中相同的材料参数和截面属性，并在与实验一致的距离上采用Conwep算法施加相同的爆炸载荷，分别计算了不同工况下的背板挠度，并将计算结果与实验中得到的挠度进行对比，结果发现：有限元计算得到的最终挠度wcal与实验测量的挠度值wexp吻合较好，如图8所示。因此可以认为本文中所采用的有限元算法、材料本构模型、初始条件和边界条件均是可靠的。

2.2.2夹芯梁与实体梁对比分析

通常情况下，被保护人和物体一般都在背爆面即夹芯结构的后面板处，所以关于夹芯结构的抗爆性能诸多学者采用后面板的残余挠度来进行考量。但是，对于金属夹芯结构后面板的残余挠度并不是响应阶段的最大挠度，两者之间存在1个弹性回弹量，因此有可能会误导设计人员进行安全防护设计[18]。图9给出了在150 mm距离施加150 g炸药爆炸当量下，实体梁和夹芯梁(OC-1)的挠度时程和塑性能量耗散时程曲线。从图9(a)中可以得到，夹芯梁的挠度时程曲线由于存在芯层压缩和前面板塑性变形的原因在0.5 ms之前变化较小，随着芯层逐渐压缩，后面板开始产生较大的塑性变形。并且夹芯梁的挠度37.35 mm比实体梁的挠度46.82 mm减小9.47 mm，减小约20.23%；夹芯梁整体的塑性耗散能量为1464.64 J较实体梁的塑性耗散能量513.43 J增加951.21 J，增长约1.85倍。图9(b)给出了实体梁和构成夹芯梁的三部分以及夹芯梁整体的塑性耗散能量时程，从图中可以发现夹芯梁的芯层在塑性能量耗散方面起主要作用，芯层能量耗散约为整体能量耗散的56.63%。

为研究不同爆炸载荷作用下夹芯梁的能量吸收能力，采用5种不同的炸药当量(对应5种比距离)施加在夹芯梁上，并与实体梁进行对比，如图10所示。从图10(a)中发现，夹芯梁和实体梁的后面板挠度与比距离不成线性关系；随着比距离的逐渐增大两种梁的后面板挠度均在减小，且在研究范围内夹芯梁的抗爆性能优于实体梁。图10(b)给出了不同载荷强度下夹芯梁和实体梁的塑性能量耗散。结果发现塑性能量耗散与比距离不成线性关系，且随着比距离的逐渐增大其耗散的能量逐渐地降低；芯层塑性耗散的能量比率逐渐上升，在比距离小于0.32时，其增长趋势较为平缓；当比距离大于0.32时，其增长比率较大；芯层能量耗散比率在五种爆炸载荷下都高于50%，说明芯层是夹芯梁的主要吸能部件。

2.2.3不同芯层夹芯梁对比分析

为了研究不同初始折角对由其所构成蜂窝胞元组成的夹芯梁抗爆性能的影响，对5种不同的爆炸载荷施加在由4种不同折叠芯层所组成的夹芯梁上的动态响应进行分析。图11给出了在距离上面板中心点150 mm处施加150 g TNT爆炸当量作用下实体梁和4种不同芯层夹芯梁的挠度时程和能量耗散时程曲线。从图11(a)中发现，4种不同夹芯梁的后面板挠度均小于实体梁，且3种曲边蜂窝(OC-1、OC-2、OC-3)的挠度均小于直边蜂窝(OC-4)。从图11(b)中发现，4种夹芯梁的能量吸收均比实体梁大，3种曲边蜂窝夹芯梁的能量吸收差别较小，且略高于直边蜂窝夹芯梁。主要原因是由于曲边蜂窝的初始折角对蜂窝芯层的塑性屈曲具有引导作用，大大减小了其屈曲载荷，使得芯层更早进入渐进压缩状态产生较大的塑性变形来实现能量耗散的作用。

为了对比分析在不同爆炸载荷作用下4种夹芯梁的能量吸收能力，采用5种不同的炸药当量(对应5种比距离)施加在夹芯梁上面板，其挠度及能量耗散如图12所示。从图12(a)中发现，随着比距离的增大挠度逐渐降低但不呈现线性关系，在比距离为0.238时4种夹芯梁的挠度很相近；当比距离大于0.238时，曲边蜂窝夹芯梁的抗爆性能明显有于实体梁，而直边蜂窝夹芯梁介于两者之间。从图12(b)看出，随着比距离的增大，夹芯梁整体塑性耗散能量逐渐下降并呈现非线性关系，而芯层能量吸收比率随比距离的增大逐渐增大。当比距离为0.238时，直边方孔蜂窝的吸能比率是4种芯层中最小的；随着比距离的增大，直边蜂窝比3种曲边蜂窝芯层的能量吸收比率大，且随着初始折角的增大芯层吸能比率逐渐增大。

3 结 论

采用有限元软件Abaqus/explicit对准静态载荷和爆炸载荷作用下可折叠芯层以及由其组成夹芯梁的力学响应进行了分析，采用后面板最大挠度作为其抗爆性能的评价指标。比较了实体梁和夹芯梁在不同爆炸载荷作用下后面板挠度及能量吸收机理。在本文中研究的载荷范围内得到以下主要结论：

(1)可折叠曲边蜂窝芯层在准静态载荷作用下具有一定的负泊松比效应，且初始折叠角对其具有较大影响。

(2)在爆炸载荷作用下夹芯梁的抗爆性能优于实体梁，且其主要的能量吸收部件为多孔金属芯层。

(3)在爆炸载荷作用下可折叠蜂窝的初始折角对其作为芯层夹芯梁的抗爆性能有较大影响，随着初始折角逐渐增大，其抗爆性能逐渐减弱；当初始折角为直角时对应于方孔直边蜂窝，其抗爆性能最差。

[1] 王志华,朱峰,赵隆茂.多孔金属夹芯结构动力学行为及其应用[M].北京:兵器工业出版社,2010.

[2] RUSSELL B P, LIU T, FLECK N A, et al. The soft impact of composite sandwich beams with a square-honeycomb core[J]. International Journal of Impact Engineering, 2012,48(1):65-81.

[3] LIU Y, ZHANG X C. The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs[J]. International Journal of Impact Engineering, 2009,36(1):98-109.

[4] MCSHANE G J, RADFORD D D, DESHPANDE V S, et al. The response of clamped sandwich plates with lattice cores subjected to shock loading[J]. European Journal of Mechanics A/Solids, 2006,25(2):215-229.

[5] LV C, KRISHNARAJU D, KONJEVOD G, et al. Origami based mechanical metamaterials[J]. Scientific Reports, 2014(4):5979.DOI:10.1038/srep05979.

[6] MORI O, SAWADA H, FUNASE R et al. First solar power sail demonstration by IKAROS[J]. Transactions of the Japan Society for Aeronautical and Space Sciences Aerospace Technology Japan, 2010,8(27):25-31.

[7] TSUDA Y, MORI O, FUNASE R, et al. Flight status of IKAROS deep space solar sail demonstrator[J]. Acta Astronautica, 2011,69(9):833-840.

[8] ZIRBEL S A, LANG R J, THOMSON M W, et al. Accommodating thickness in origami-based deployable arrays[J]. Journal of Mechanical Design, 2013,135(11):111005-11.

[9] LIU Zhengyou, ZHANG Xixiang, MAO Yiwei, et al. Locally resonant sonic materials[J]. Science, 2000,289(5485):1734-1736.DOI: 10.1126/science.289.5485.1734.

[10] MALDOVAN M. Sound and heat revolutions in phononics[J]. Nature, 2013,503(7475):209-217.DOI:10.1038/nature12608.

[11] GRZESCHIK M, FISCHER S, DRECHSLER K. Potential of high performance foldcores made out of PEEK polymer[C]∥SAMPE Europe Technical Conference and “Table-Top” Exhibition 2009. Bristol, United Kingdom, 2009:94-101.

[12] HEIMBS S, MIDDENDORF P, KILCHERT S, et al. Numerical simulation of advanced folded core materials for structural sandwich applications[C]∥The 1st European Air and Space Conference. Deutscher Luft-und Raumfahrt Kongress. Berlin, Germany, 2007:2889-2896.

[13] HEIMBS S, MIDDENDORF P, KILCHERT S, et al. Experimental and numerical analysis of composite folded sandwich core structures in compression[J]. Applied Composite Materials, 2007,14(5/6):363-377.

[14] HEIMBS S. Virtual testing of sandwich core structures using dynamic finite element simulations[J]. Computational Materials Science, 2009,45(2):205-216.

[15] WACHINGER G, ANGERER E, MIDDENDORF P, et al. Impact protection structures for composite fuselage application[C]∥SAMPE Europe International Conference. Paris, France, 2008:271-277.

[16] IMBALZANO G, TRAN P, NGO T D, et al. A numerical study of auxetic composite panels under blast loadings[J]. Composite Structures, 2016,135(1):339-352.

[17] GERETTO C, CHUNG KIM YUEN S, NURICK G N. An experimental study of the effects of degrees of confinement on the response of square mild steel plates subjected to blast loading [J]. International Journal of Impact Engineering, 2015(79):32-44.DOI:10.1016/j.ijimpeng.2014.08.002.

[18] YAHAYA M A, RUAN D, LU G, et al. Response of aluminium honeycomb sandwich panels subjected to foam projectile impact: An experimental study[J]. International Journal of Impact Engineering, 2015,75(1):100-109.