高光谱图像压缩方法

陈玉玲，闫敬文，马丽梅

(1.北京邮电大学 网络空间安全学院，北京 100876；2.贵州广播电视大学 信息工程学院，贵州 贵阳 550023；3.汕头大学 电子工程系 广东省数字信号与图像处理技术重点实验室，广东 汕头 515063；4.河北师范大学 河北省网络与信息安全重点实验室，河北 石家庄 050024)

0 引 言

高光谱遥感卫星图像主要有谱段与谱段间相关性及空间相关性两种冗余，为了消除这些相关性，文献[1,2]采用三维矢量量化和三维小波变换等方法用分离三维处理方法先后消除谱相关性和空间相关性。基于空间域采样的近似算法使用波段预处理，适当选取采样步长，能在几乎不影响压缩算法性能的情况下，大幅降低计算量[3]，用线性预测和多谱带查表相结合的高光谱图像无损压缩算法，去除这些图像中因校正引起的信息冗余也得到了较高的压缩比[4]，文献[5]提出了基于分类KLT的压缩算法，利用光谱信息对高光谱图像进行地物分类，根据相邻波段的相关性对高光谱图像进行波段分组。在地物分类与波段分组的基础上，对每组的每一类地物数据分别进行KL变换，利用EBCOT(embedded block coding with optimal truncation)算法对所有主成分进行联合编码，实现高光谱图像的有效压缩。对于高光谱图像压缩的研究方向主要集中在大数据、智能化带来的技术挑战上，基于混合预测的高光谱图像无损压缩[6]、基于切片映射的张量分解方法[7]和结合人眼对比度敏感视觉特性的图像压缩[8]顺应了发展前沿和热点论题[9]，达到了更好的压缩效果。

近几年，基于小波变换[10]和小波域子的研究[11]突破了传统的压缩算法框架，消除了光谱和空间冗余，提高了压缩比，但是高光谱图像的特性受影响。基于独立成份[12]和分类KLT的压缩方法[5]保留了高光谱图像的光谱特性，但是计算复杂度大大提高。

针对这些不足和需要改进之处，本文提出一种基于自适应分组KL变换的高光谱图像方法。首先针对不同图像数据的谱相关性变化情况，自适应地对图像数据进行分组，能够充分利用高光谱图像的谱相关性，避免细节信息的丢失。然后对分组后的图像数据进行改进式分块KL变换。考虑到提高算法运行速度和节省资源，对经过KL变换处理的图像数据采用整数小波变换和SPIHT算法进行压缩编码，实现整个系统的准无损压缩。

1 基于APKLT/IWT/SPIHT算法的高光谱图像压缩算法

基于APKLT/IWT/SPIHT算法的高光谱图谱压缩系统如图1所示。根据光谱图像各个相邻连续谱段之间的谱间相关性的波动特性，组合高相关性的谱段并分别进行改进式KL变换，消除图像在光谱维上的谱相关性，采用整数9/7小波变换和SPIHT算法对输出的均值图像、本征值和本征矢量进行压缩编码。对低相关性的谱段直接进行三维整数小波变换/三维SPIHT算法(3D IWT/3D SPIHT),进行压缩编码。对低相关性组进行三维整数小波变换时除了高光谱的操作外，还增加了光谱维的变换。在自适应分组的同时，取出各个谱段并标注每个原始谱段的初始顺序，在压缩完成以后根据所记录的各个谱段的初始顺序，把各个谱段各自放回到原来位置，重组原光谱图像。

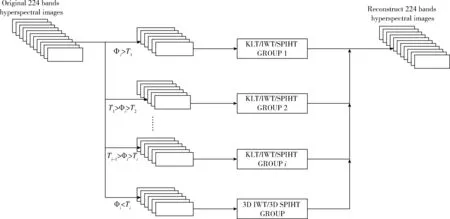
图1 基于APKLT/IWT/SPIHT的高光谱图谱压缩系统

为尽可能的消除高光谱图像的谱冗余，又可以通过合理减少本征值的个数来降低KL变换的运算量，算法采用改进式KL变换去除高光谱图像的谱冗余信息，其产生的压缩比

(1)

其中，n×n表示所分的子块大小，k是保留的本征值的个数，Q为谱段数。本文采用的改进式KL变换取前两个本征值，即k=2。所取分块大小n×n由谱段数Q决定，表1中根据每组谱段数分别取了8×8和4×4两种分块。谱段数大于64组的用8×8块的KL变换，谱段数小于64的组用4×4块的KL变换。对224谱段的高光谱图像数据，取Q为224，子块是8×8，k取2，代入式(1)，算得改进式KL变换的压缩比CR为22.4；若Q为64，子块是4×4，k取2，则压缩比CR为5.8。

表1 谱段重组中的阈值选取和KL变换中的分块尺寸

1.1 高光谱图像谱间相关性分析

假定高光谱图像第i谱段的图像为fi(x,y)，第i+1谱段的图像为fi+1(x,y)，则式(2)为第i谱段的谱间相关系

(2)

其中

(3)

(4)

图2是本文实验所用的224谱段的16 bit高光谱图像的谱间相关系数曲线。由图形得出，高光谱遥感图像的谱间相关系数波动较大，波动范围为0.1-1。

图2 224谱段高光谱图像谱间相关系数曲线

1.2 自适应分组算法

由于谱相关性波动较大，如果对整个224谱段的高光谱图像进行KL变换，并没有充分利用谱间相关性的波动特性，且可能丢失很多细节信息。针对这个问题，本文设计了一种适合于任意谱段数的高光谱图像的自适应谱段分组的处理方法。分组时要遵循几个原则：

(1)高相关性的连续谱段分在同一组；

(2)由于本文采用整数小波变换对每组光谱经KL变换以后的均值矩阵，特征值矩阵，特征向量矩阵分别进行处理。而特征向量矩阵的第二维就是每组的谱段数目，则要求每组谱段数P要可以被2的整数次方整除，即P=n*2i(i,n是整数，其中i与整数小波分解层数有关)；

(3)根据KL变换的压缩要求，为了获得有效的压缩，根据式(1)，则要求每组段数p≥n×n(其中n×n是KL变换的分块大小)。

根据以上分组原则，自适应谱段分组方法的大致步骤是先确定需要分组的数目N，找出N-1个最佳分段相关系数阈值RX；根据得到的N-1个最佳相关系数阈值RX把原始高光谱图像划分为N组；划分谱段的过程中，记录各个谱段的初始顺序，以便压缩完毕可以准确地重建原始高光谱图像。

自适应分组的具体步骤为：假设要把一个M谱段的高光谱图像分成N组。在满足分组的几个原则的前提下，按照上述几个步骤具体划分。按照一般性的要求，先假定要求一组有L个谱段，初始化一个相关系数阈值T=1，然后每次T递减一个很小的步长Δ；对每个T值计算相关系数大于这个阈值的谱段的个数，当谱段个数P满足P=n*2i(i,n是整数)时，保存T，最后得到N-1个符合要求的阈值{T1,T2,…TN-1}，这些保存下来的阈值为我们所要得到的最佳阈值。把相关系数大于T1的各个谱段放在第一组，把相关系数在T1和T2之间的各个谱段放在第二组，依次操作，把相关系数小于TN-1的谱段放在第N组。而且谱相关性从第1组到第N组逐渐递减。

不同组根据谱段数目差异，采用不同分块尺寸的KL变换来消除谱相关，对于谱相关性很低的那一种谱段则不再做KL变换。本文算法中，对于自适应分段后的最低相关性组不做KL处理。在压缩完毕以后，根据分组过程中所记录的原始高光谱各个谱段的初始顺序，把各个谱段重新放回去，可以准确地重建原始高光谱图像。本文实验中采用224谱段的高光谱图像，表1为各种分组方法的分组情况。

2 实验结果和讨论

实验中采用图像大小为128×128的224谱段高光谱图像。采用5种方法进行压缩：①non-adaptive-A：KLT/IWT/SPIHT；②non-adaptive-B：32-PKLT/IWT/SPIHT；③adaptive-C：192+32-APKLT/IWT/SPIHT；④adaptive-D：96*2+32-APKLT/IWT/SPIHT；⑤adaptive-E：64*3+32-APKLT/IWT/SPIHT。

当压缩比CR=90倍的时候，通过采用自适应和非自适应方法各谱段PSNR对比曲线。得出，adaptive-C方法的整体压缩效果最好，而non-adaptive-B方法的压缩效果最差。

从图3可以看出，adaptive-C方法的PSNR比non-adaptive-A 和non-adaptive-B方法提高了约5 db-6 dB。图4是CR=90时，自适应和非自适应方法第88谱段的压缩效果对比。

图3 自适应和非自适应方法不同压缩率下PSNR曲线对比

图4 自适应和非自适应方法第88谱段压缩效果

从图5的运行时间曲线对比可以看到，采用谱段分组KL变换压缩光谱图像的方法，在各个不同比特率情况下，其运行速度都比不分段处理要快。而等间隔分7组压缩光谱图像所耗用时间最短，比不分组的224段光谱直接压缩整体平均运行时间减少264 s。自适应分两组的方法运行时间比不分组的224段光谱直接压缩整体平均运行时间平均减少了约70 s。综合图3和图5，基于自适应分组KL变换的光谱压缩方法，压缩图像的效果最优；而基于非自适应等间隔分组KL变换的方法运行速度最快，基于自适应分组KL变换的方法速度次之。综合评价，与不分组224段谱图像直接压缩相比，采用自适应分谱段压缩光谱图像不论在提高图象质量还是运行速度方面都有很大的优势。

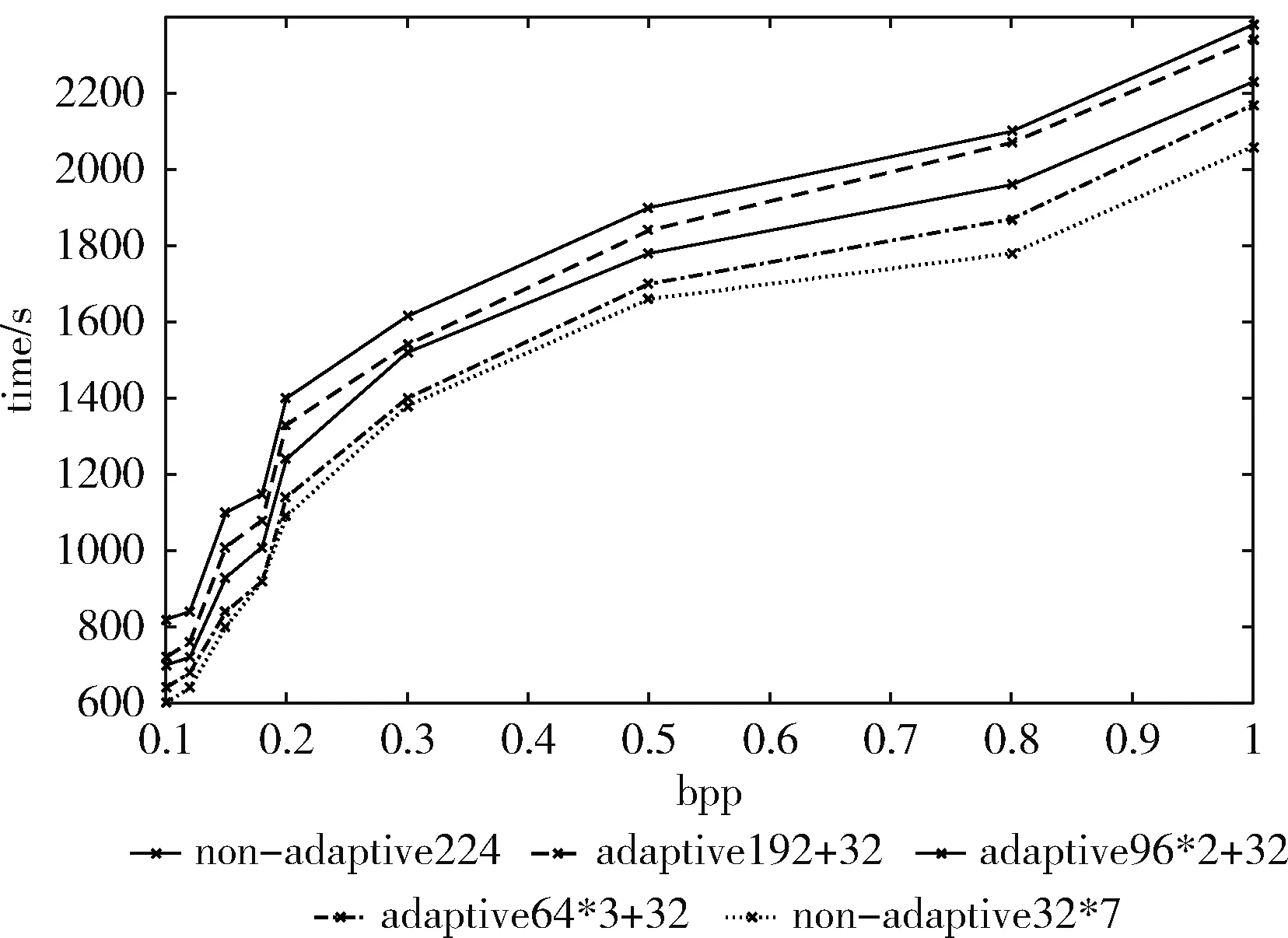
图5 运行时间对比曲线

(1)光谱数据的总谱段数目是有限的，如果分组数目过多，每组谱段数目就很少。由式(1)分析可以知道，如果每组的谱段数目过少(小于KL变换分块大小n×n)的话KL变换所产生的压缩倍数将会急剧下降。如此，为了提高综合压缩倍数，产生符合要求的压缩率，就必须要在SPIHT编码压缩过程中成倍地降低比特率，这样就会降低光谱的整体压缩性能。因此，谱段不宜分为过多组；

(2)本文分5种方法进行实验对比：非自适应不分组non-adaptive-A、非自适应等间隔分组non-adaptive-B、本文设计的自适应分两组adaptive-C(192+32)、自适应分3组adaptive-D(96*2+32)和自适应分4组adaptive-E(64*3+32)。实验结果表明，本文设计的基于自适应分组KL变换的高光谱图像压缩方法，可以获得非常理想的压缩性能；

(3)综合图3和图5，在同等比特率时，采用本文设计的自适应分两组adaptive-C方法比非自适应不分组non-adaptive-A 方法获得的PSNR值高出约5个dB；而采用自适应adaptive-D和adaptive-E方法也都可以获得明显优于非自适应方法的性能；

(4)采用非自适应等间隔分组non-adaptive-B方法压缩图象重建效果相对最差。从图5运行时间对比，可以看到采用本文设计的自适应分两组adaptive-C方法比非自适应不分组non-adaptive-A方法直接压缩运行时间平均减少了约70 s；采用非自适应等间隔分组non-adaptive-B方法运行时间最短。综合图像质量和运行时间两个指标，采用基于自适应分组KL变换的方法压缩光谱图像的效果明显优于基于非自适应不分组KL变换和非自适应等间隔分组的方法；

(5)本文提出的基于分组KL变换的压缩方法尤其适合处理多谱段且谱间相关性波动相对较大的高光谱数据。因为这种数据在直接KL变换时将会丢失相对更多的细节信息，这种情况下本文的方法就可以体现出明显的优势。随着光谱图像正朝着多谱段方向发展，本文提出的基于自适应分组KL变换的高光谱图像压缩方法将会有很大的发展前景。

3 结束语

根据多谱段高光谱图像连续若干谱段具有很强的相关性，而每间隔若干谱段相关性就会有很大波动的特点，本文设计了一种根据高光谱图像谱相关性，自适应分谱段进行分组KL变换的高光谱图像数据压缩方法(APKLT/IWT/SPIHT)。分组后每组光谱都具有相对集中的高相关性，使得KL变换可以把光谱的细节信息尽可能多地保存下来，理论上可以达到更优的效果。为了提高运行速度，本文方法采用的是第二代整数提升小波。在未来的工作中，可以考虑应用超小波变换来代替本文的整数小波变换，以期获得更好的压缩性能。为了进一步提高实时性，需要对各自适应分组的组应用平均相关系统的DCT变换替换KL变换，进一步提高运行速度，也便于DSP实现。

[1]Karami A,Yazdi M,Mercier G.Compression of Hyperspectral images using discrete wavelet transform and tucker decomposition[J].IEEE J-STARS,2012,5(2):444-450.

[2]Ye Z,Prasad S,Li W,et al.Classification based on 3-D DWT and decision fusion for hyperspectral image analysis[J].IEEE Geoscience and Remote Sensing Letters,2014,11(1):173-177.

[3]HONG Heng,HE Mingyi.An approximate algorithm for correlation matrix computation in Hyperspectral image compression[J].Electronic Design Engineering,2013,21(12):128-131(in Chinese).[洪恒,何明一.一种适于高光谱图像压缩的相关系数矩阵近似计算算法[J].电子设计工程,2013,21(12):128-131.]

[4]SONG Jinwei,ZHANG Zhongwei,CHEN Xiaomin.Hyperspectral imagery compression via linear prediction and lookup tables[J].Optics and Precision Eengineering,2013,21(8):2201-2208(in Chinese).[宋金伟,张忠伟,陈晓敏.利用线性预测与查表法的高光谱图像压缩[J].光学精密工程,2013,21(8):2201-2208.]

[5]FANG Lingjiang,NIAN Yongjian,WANG Yingchun.Hyperspeetral images compression based on classified KLT[J].Computer Technology and Development,2013,23(11):82-86(in Chinese).[方凌江,粘永健,王迎春.基于分类KLT的高光谱图像压缩[J].计算机技术与发展,2013,23(11):82-86.]

[6]LI Yuanyuan,JING Wenbo,LIU Xue,et al.Lossless compression of Hyperspectral images using hybrid prediction[J].Journal of Changchun University of Science and Technology(Natural Science Edition),2016,39(1):77-81(in Chinese).[李媛媛,景文博,刘学,等.基于混合预测高光谱图像无损压缩[J].长春理工大学学报(自然科学版),2016,39(1):77-81.]

[7]WAN Chenkun,WANG Bin.A novel approach to evaluate nonlinear correlation of a multivariabe data set[J].Journal of Fudan University(Natural Science),2016,54(6):696-705(in Chinese).[万晨坤,王斌.基于切片映射张量分析的高光谱图像压缩[J].复旦大学学报(自然科学版),2016,54(6):696-705.]

[8]YAO Juncai.Color image compression algorithm combining the human contrast perception characteristics[J].Chinese Journal of Liquid Crystals and Displays Characteristics,2016,31(6):584-594(in Chinese).[姚军财.一种结合人眼对比度感知特性的彩色图像压缩算法[J].液晶显示,2016,31(6):584-594.]

[9]DU Peijun,XIA Junshi,XUE Zhaohui,et al.Review of Hyperspectral remote sensing image classification[J].Journal of Remote Sensing,2016,20(2):236-256(in Chinese).[杜培军,夏俊士,薛朝辉,等.高光谱遥感影像分类研究进展[J].遥感学报,2016,20(2):236-256.]

[10]LI Jin,JIN Longxu,LI Guoning.Hyper-spectral remote sen-sing image compression based on nonnegative tensor factorizations in discrete wavelet domain[J].Journal of Electronics and Information,2013,35(2):489-493(in Chinese).[李进,金龙旭,李国宁.离散小波变换域非负张量分解的高光谱遥感图像压缩[J].电子与信息学报,2013,35(2):489-493.]

[11]HUANG Risheng.An improved wavelet domain vector Hyperspectral image noise reduction processing technology[J].Bulletin of Science and Technology,2014,30(8):149-151(in Chinese).[黄日胜.一种改进的小波域子矢量高光谱图像压缩处理技术[J].科技通报,2014,30(8):149-151.]

[12]BAI Lin,GAO Tao.Hyperspectral images lossy compression method based on independent components analysis[J].Computer Engineering,2013,39(3):245-249(in Chinese).[白璘,高涛.基于独立成分分析的高光谱图像有损压缩方法[J].计算机工程,2013,39(3):245-249.]