点云的刚体运动参数估计方法的比较

袁志聪，鲁铁定，邓小渊

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.流域生态与地理环境监测国家测绘地理信息局重点实验室，江西 南昌 330013)

近年来，随着三维激光扫描技术的不断发展，点云获取的速度越来越快，如何高效地处理海量点云数据已成为科研领域的研究热点。点云配准是海量点云数据处理中的核心问题；点云配准就是要使所有来自两个点云集合中的同名点对满足同一刚体变换[1-2]，如何快速准确地求解刚体变换参数成了点云配准中的核心问题。

传统的坐标转换采用布尔沙七参数模型[3],由于布尔沙模型的旋转矩阵是由坐标轴之间的夹角表示的，其表示方式繁琐，计算复杂，同时存在象限判断难等问题，文献[4]提出基于罗德里格矩阵的求解方法，罗德里格矩阵由3个独立参数组成旋转矩阵，结合最小二乘法具有精度高，速度快等优点。常用的刚体运动估计方法还有奇异值分解法；正交分解法[5]；四元数法[6-7]等。宋林霞[8]通过奇异值分解法求解旋转矩阵，并提出一条相关引理，将距离优化问题转为估计的最优的旋转矩阵R使得对于任意给定的方阵A都有tr(ATR)最大，对算法进行优化。邱志强[9]等提到基于三维特征点以及二维特征点的“8点算法”的刚体运动估计方法。官云兰[10-11]应用单位四元数进行刚体运动估计，四元数法具有计算速度快、稳定性好等优点，代俣西[12]在基于对偶四元数的三维运动估计中介绍对偶四元数的估计方法。对偶四元数是对偶数和四元数的结合，具备其他方法所没有的优点，对偶四元数能同时求解旋转矩阵和平移参数，计算过程中不会引入旋转矩阵的误差。

本文在现有基础上，通过模拟数据和实例对奇异值分解法、正交分解法、单位四元数法和对偶四元数法4种估计方法作比较，分析4种方法的优缺点，得出对偶四元数总体性能最优。

1 刚体运动及参数求解方法

1.1 刚体运动

(1)

式中:R为3×3正交单位矩阵，称为旋转矩阵;T为3维列向量，称为平移向量。

刚体运动估计就是在目标函数F(R,T)=min的情况下求解最优的旋转矩阵R,平移向量T，使得两点集尽可能的重合。目标函数具体形式为

(2)

1.2 刚体运动参数求解方法

1.2.1 单位四元数法

四元数是数学家Hamilton创造的；可以认为是一个包含四个元素的列向量，可表示为

q=w+xi+yj+zk.

(3)

式中:w为标量，(x,y,z)为四元数对应的向量。四元数亦可写为q=(w,v)。

定义4阶矩阵

(4)

设矩阵S最大特征值对应的单位特征向量为q=(q0,q1,q2,q3)，则对应的旋转矩阵为

(5)

平移向量为

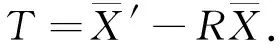
(6)

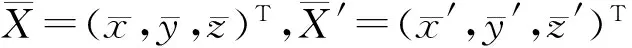
1.2.2 奇异值分解法(SVD)

首先求出运动前后两点集的重心化坐标

Pi=Pi-Pio,

(7)

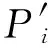
(8)

R=VUT.

(9)

平移向量为

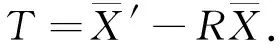
(10)

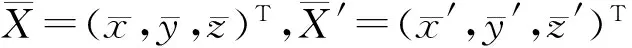
1.2.3 正交分解法(OD)

设矩阵HHT的特征值分别为λ1，λ2，λ3，对应的特征向量分别为u1,u2,u3。旋转矩阵可表示为

(11)

平移向量为

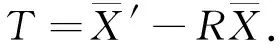
(12)

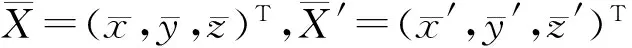
1.2.4 对偶四元数法(DQD)

对偶四元数是由Clifford提出来的,是对偶数和四元数的组合，可以理解为元素为四元数的对偶数,同样可理解为元素为对偶数的四元数,对偶四元数的优越性体现在它继承了二者的共性，从而能够统一表示旋转和平移。对偶四元数可表示为

ε(q00,q01,q02,q03)T.

(13)

式中q，q0均为四元数，分别称做对偶四元数的实部和对偶部，ε为对偶算符。

对偶四元数的空间变换如图1所示。n是单位向量，是空间旋转和平移的变换方向。传统的坐标转换是先通过坐标轴进行旋转变换，再通过平移向量t完成平移变换，形成新的坐标系，对偶四元数空间变换首先将原始坐标系沿着n方向平移距离d，然后围绕过点p的直线n旋转角度θ，即可得到转换后的坐标系。

图1 对偶四元数空间变化

设点p=(x,y,z)T刚体运动后变为p′=(x′,y′,z′)T，可用对偶四元数表示刚体运动，即

(14)

(15)

(16)

2 实例验证

2.1 模拟数据与结果分析

利用Matlab随机生成1 000个数据得到点云A，如图2所示，给定初始旋转矩阵和平移向量；对点云A进行刚体运动变换，得到点云B，现通过4种方法分别求解刚体运动参数，把旋转矩阵转换为旋转角，以求得的旋转矩阵对应的旋转角与初始旋转矩阵对应的旋转角之间的差作为旋转角误差；对应的平移向量之间的差作为平移向量误差。

已知两点云的变换参数如表1所示。

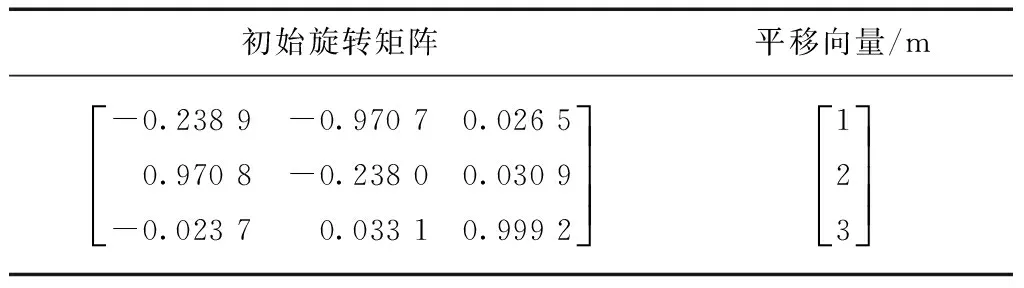
表1 两点云变换参数

图2 两点云相对位置

目标点云不加噪声情况下，4种方法求得的转换参数如表2所示。

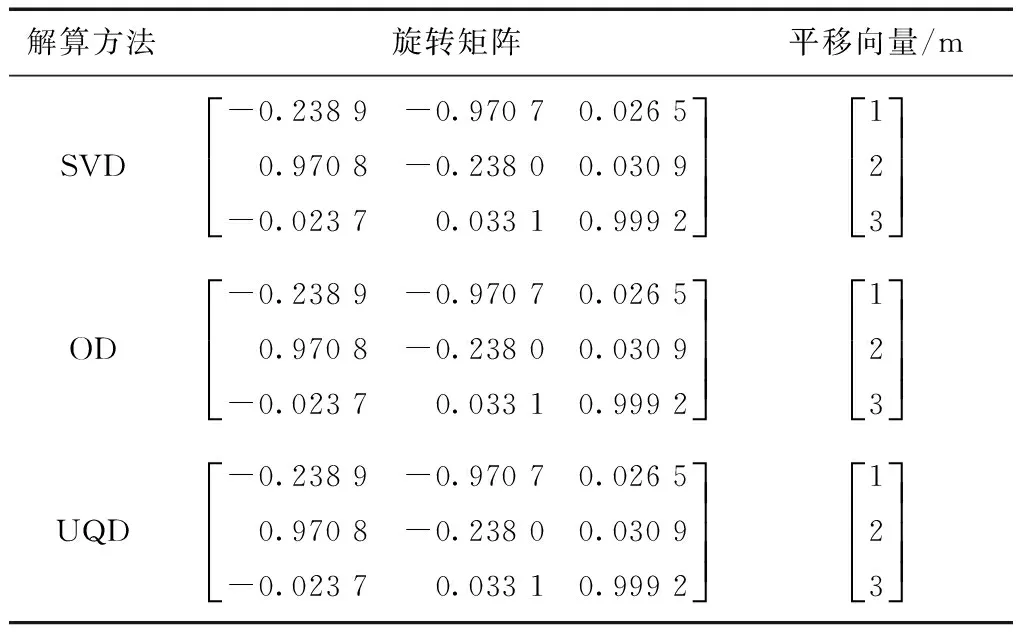
表2 不加噪声的情况

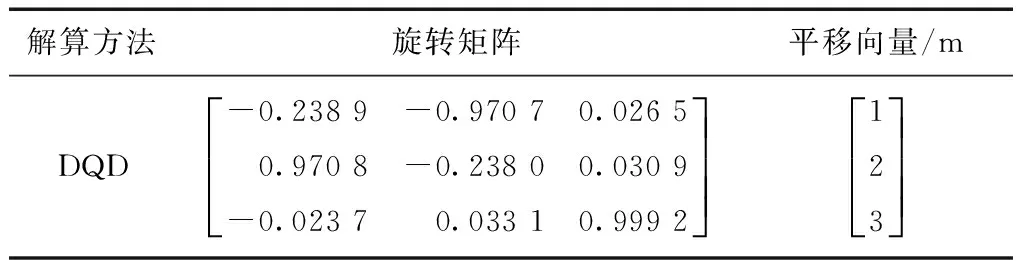
续表2

下面将旋转矩阵转换为角度，计算不同噪声水平下的参数误差，算式为

(17)

(18)

加标准差为0.2的噪声的参数误差如表3所示。

表3 加标准差为0.2的噪声计算2 000次的参数误差

加标准差为0.4的噪声的参数误差如表4所示。

表4 加标准差为0.4的噪声计算2 000次的参数误差

加标准差为0.6的噪声的参数误差如表5所示。

表5 加标准差为0.6的噪声计算2 000次的参数误差

加标准差为0.8的噪声的参数误差如表6所示。

表6 加标准差为0.8的噪声计算2 000次的参数误差

加标准差为1.0的噪声的参数误差如表7所示。

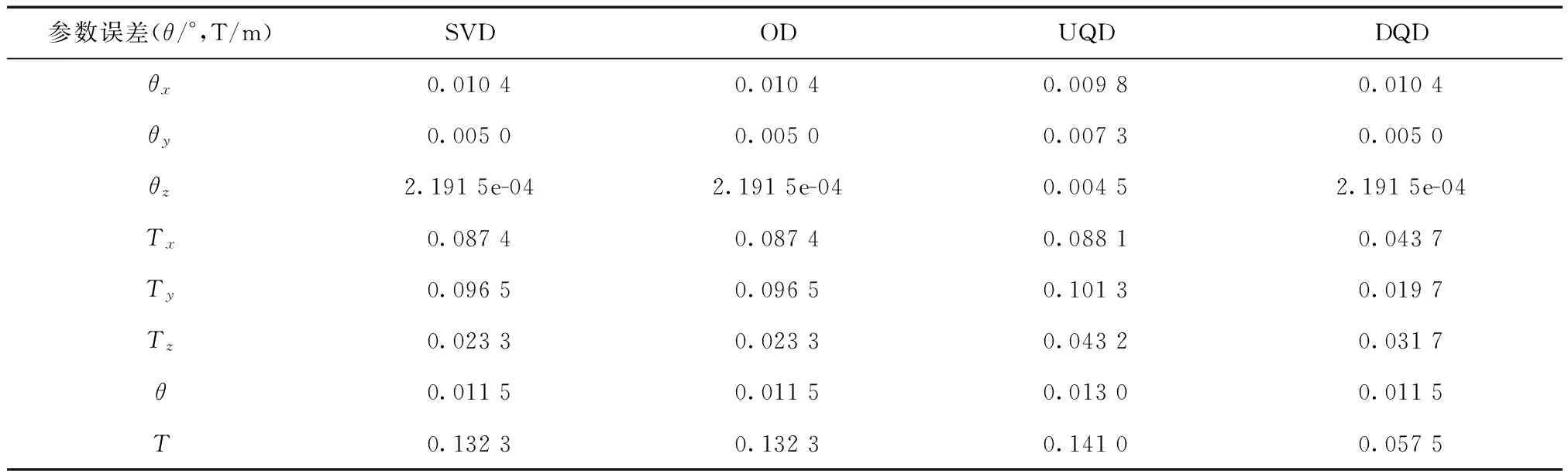
表7 加标准差为1.0的噪声计算2 000次的参数误差

4种方法计算2 000次所耗时间如表8所示。

表8 计算2 000次耗时

噪声标准差与角度误差之间的关系如图3所示。

图3 噪声标准差与角度误差之间的关系

噪声标准差与平移参数误差之间的关系如图4所示。

图4 噪声标准差与平移参数误差之间的关系

由表2数据可知，在目标点云不加噪声的情况下，4种刚体运动参数求解方法具有相同的精度，且与初始旋转矩阵；平移向量结果一致。由表3—表7数据可知，当目标点云加入随机噪声时，对于旋转矩阵的估计，奇异值分解法、正交分解法、对偶四元数法三者具有相同的精度，均优于四元数的求解精度，以表7数据为例，前3种方法的求解误差为0.011 5，而四元数的求解误差为0.013 0，图3所示的折线图可以明显看出4种方法噪声水平对角度估计误差的影响。

对于平移向量的求解，通过表3—表7数据可得出对偶四元数法精度最高，稳定性最好；体现了对偶数和四元数的优良性质。以表7数据为例，当噪声标准差达到1.0时，对偶四元数的参数误差为0.057 5，四元数参数误差0.141 0，奇异值分解法和正交分解法具有相同的精度，参数误差均为0.132 3。由图4可得出平移参数求解误差与噪声标准差之间的关系。对偶四元数精度最高的原因在于求解变换参数时，旋转矩阵和平移向量同时求解，平移向量不会引入旋转矩阵所带来的误差。

通过实验数据分析，可知：

1)在目标点云不含任何误差时，4种刚体运动参数求解方法具有相同的求解精度，均满足实际工程的需求。

2)在误差水平相同的情况下，奇异值分解法，正交分解法、对偶四元数法对于旋转矩阵的估计具有相同的精度，优于四元数的求解。对于平移参数的估计，对偶四元数求解精度最高，奇异值分解法与正交分解法具有相同的精度，优于四元数求解精度。

3)在计算速度方面，由快到慢依次为奇异值分解法、四元数法、正交分解法、对偶四元数法。

4)在综合性能方面，对偶四元数综合性能最优。

2.2 实测数据分析

以实测的点云数据为例，如图5所示，图中两平面点云是不同视角下获得的点云数据，已知两者之间的变换参数，现分别通过4种方法求解刚体变换参数。

图5 两平面点云相对位置

两平面点云的已知变换参数如表9所示。

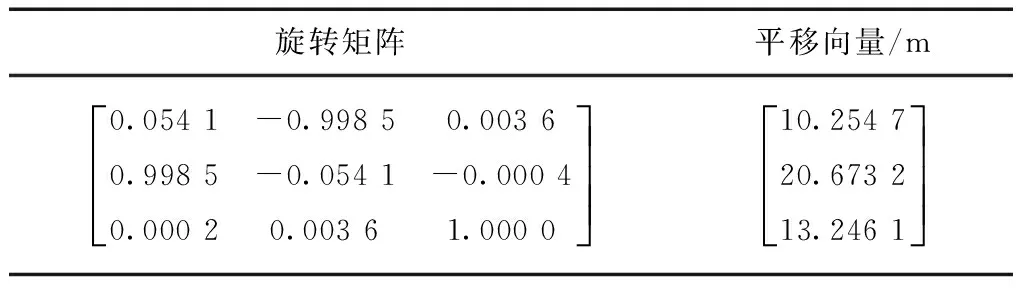
表9 两点云变换参数

4种方法求得的转换参数如表10所示。

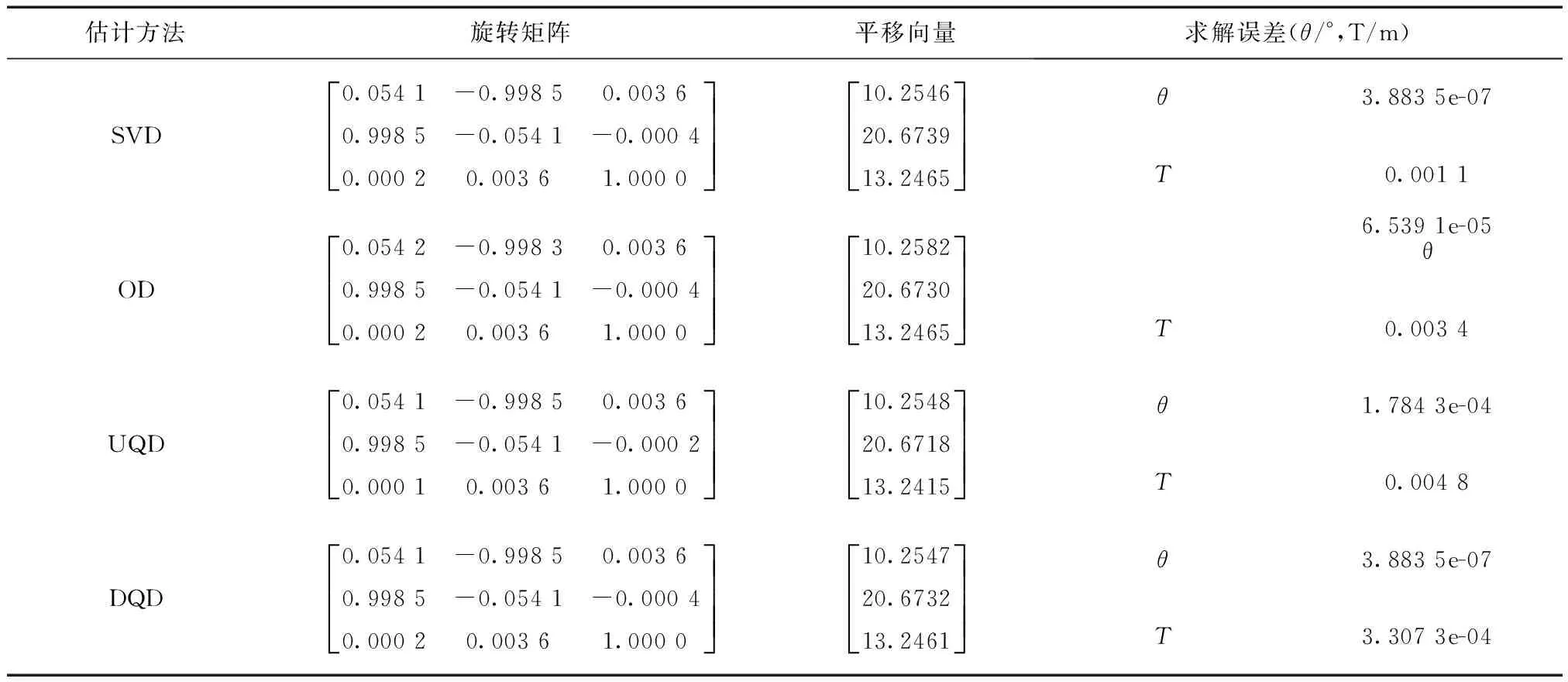
表10 4种方法求得的转换参数

通过实测数据求解，由表10数据可知，对偶四元素总体性能优于其他三种算法，由图6可知，经过对偶四元数求解的刚体变换参数；两点云很好的重合在了一起。对偶四元数法满足实际工程的需求。

对偶四元数配准后两点云的相对位置如图6所示。

图6 对偶四元数配准后

3 结 论

本文通过模拟仿真实验与实际算例对4种基于点云的刚体运动参数求解方法做了比较，得出以下结论：1)在目标点云不含任何误差时，4种刚体运动参数求解方法具有相同的求解精度，均满足实际工程的需求。2)在误差水平相同的情况下，奇异值分解法、正交分解法、对偶四元数法对于旋转矩阵的估计具有相同的精度，优于四元数的求解。对于平移参数的估计，对偶四元数求解精度最高，奇异值分解法与正交分解法具有相同的精度，优于四元数求解精度。3)在计算速度方面，由快到慢依次为奇异值分解法、四元数法、正交分解法、对偶四元数法。4)在综合性能方面，对偶四元数综合性能最优。相比其他3种方法，对偶四元数能够同时求解旋转参数和平移参数，平移参数不存在旋转矩阵误差累积的问题。在实际问题中，应优先使用对偶四元数求解。

本文探讨当样本数据存在偶然误差时，点云刚体运动参数估计的方法，发现基于对偶四元数的估计方法具有一定的优势；但是当样本数据中存在粗差时，本文并没有做研究，研究具有良好抗差性的点云刚体运动参数估计方法是下一步的重点。

[1] 吴嘉嘉.贝叶斯刚性点云配准的研究[D].兰州：兰州大学,2013.

[2] 林文惠.刚体运动学的几何讨论[J].力学与实践,2005,27(5):71-72.

[3] 陈宇,白征东,罗腾.基于改进的布尔沙模型的坐标转换方法[J].大地测量与地球动力学,2010,30(3):71-73.

[4] 田茂,花向红,丁鸽,等.基于罗德里格矩阵的混合最小二乘方法在三维激光中的应用[J].测绘地理信息,2014,39(2): 18-21.

[5] HORN B K P,HILDEN H M,NEGAHDARIPOUR S.Closed-form solution of absolute orientation using orthonormal matrices[J].JOSA A,1988,5(7): 1127-1135.

[6] WALKER M W,SHAO L,VOLZ R A.Estimating 3-D location parameters using dual numberquaternions[J].CVGIP: image understanding,1991,54(3): 358-367.

[7] 李志伟,李克昭,赵磊杰,等.基于单位四元数的任意旋转角度的三维坐标转换[J].大地测量与地球动力学,2017,37(1): 81-85.

[8] 宋林霞.三维点云配准方法的研究[D].济南：济南大学，2013.

[9] 邱志强,陆宏伟,于起峰.基于图像的三维刚体运动估计算法比较[J].光学技术,2004,30(1):109-112.

[10] 官云兰,程效军,周世健,等.基于单位四元数的空间后方交会解算[J].测绘学报,2008,37(1): 30-35.

[11] 官云兰.地面三维激光扫描数据处理中的若干问题研究 [D].上海: 同济大学,2008.

[12] 代俣西.基于对偶四元数的三维运动估计研究 [D].南京：南京航空航天大学,2016.