影响航空重力测量质量的若干因素分析

尹伟言，陈 真，聂 晶，刘胜震，赵 鑫

(1.国家测绘地理信息局第一大地测量队，陕西 西安 710054；2.国家测绘地理信息局测绘标准化研究所，陕西 西安 710054)

现阶段，国内航空重力测量的研究和应用逐步受到人们的重视，在欧美等发达国家，航空重力测量已经成为一种常规的重力测量手段，许多国家和地区均已开展大规模的航空重力测量[1-3]。同时，航空重力测量的应用范围也不再局限于大地测量、基准建立与维护、 地理国情监测、资源勘探等领域，还在板块运动、地球动力、自然灾害监测预防、航空地球物理勘查技术、航空航天、国防建设等方面发挥重要作用，围绕航空重力测量的新技术、新方法和新应用也在不断的发展[4-6]。其各国航空重力开展实例见表1。

我国航空重力测量发展相对滞后，高精度航空重力测量系统还在研发中，相关技术体系及应用还不够完善[7-8]。国内许多学者对航空重力测量相关技术也进行深入的研究。在前人对航空重力技术研究的基础上，通过实测数据，对影响航空重力测量质量的因素进行分析，并得出初步结论。

1 GT-2A型航空重力测量系统数学模型

测线高度处的真实重力为G，则

G=Gn+Gh+Gf.

(1)

式中：Gn为正常重力；Gh为测线高度处空间改正；Gf为实时的重力数据，也是航空重力数据处理的目标。

重力仪测量的原始重力为Fm，则

(2)

式中：vm为垂向速度；Gg为厄缶改正；ΔGd为重力仪漂移；ΔGg为随机噪声；Δv为GPS速度随机误差；ΔFp为重力仪误差。

表1 各国航空重力开展实例

测量的绝对重力为Gm，则

(3)

为了排除GPS和重力仪噪声，利用低通滤波器获得自由空间重力

(4)

其中，H为低通滤波器系数，可实现排除高频噪声的目的。

利用前校、后校的静态测量计算漂移，则

(5)

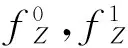
在GT-2A数据处理过程中，利用GPS求取平台速度，目前的精度可达0.02 m/s，其引起的厄缶改正的精度可在0.3 mGal以内；当前平台倾角可控制在2′以内，其引起水平加速度的影响最大仅0.27 mGal；垂直加速度精度取决于GPS测量和滤波器的性能；漂移改正每架次不超过1 mGal[9-12]。

2 实例分析

本文试验数据均来自GT-2A型航空重力测量系统，该系统属于俄罗斯制造的三轴稳定平台测量系统，数据获取类型为标量测量。设备内符合精度(重复线测量)为0.6 mGal,交叉点平差精度为1 mGal。本文所用数据均满足标称精度的要求。

试验数据来自3个试验区，数据基本情况如表2所示。

表2 试验数据基本情况表

2.1 GPS影响分析

2.1.1 接收机类型

两种基站分别采用国外Ashtech和国产South类型,置于几乎同等条件下进行试验,观测数据利用Teqc进行检查，结果表明：Ashtech数据比South数据在多路径效应和数据有效率方面有一定提高。数据质量统计见表3。

表3 Ashtech和South两种类型数据质量统计表

为进一步分析两种类型数据对航空重力测量质量的影响，分别计算滤波后的自由空间重力异常以及滤波前后的残差，结果如图1和表4所示。

图1 滤波后两种数据空间异常

表4 滤波前后残差对比表 mGal

图1表明，两种数据的自由空间重力异常相近，相差在0.5～1.34 mGal之间；而表4表明，两种数据的自由空间重力异常残差相差明显，最大达72 mGal。这说明滤波前South所获数据的噪声较大；而从整体残差来看，两种数据均在400 mGal以内，远远小于设备限差1 000 mGal。

2.1.2 基站采样率

对0.5 s和1 s两种基站数据分别计算其位置精度、空间重力异常以及滤波前后的残差，如图2—图4所示。

图2 不同采样率下的位置精度

从图2可知：0.5 s基站所确定流动站位置精度优于1 s基站，位置RMS最大差距约0.05 m；二者计算的空间重力异常有一定差异，从空间重力异常残差来看，0.5 s明显优于1 s。因此，航空重力测量中基站采样间隔应至少2 Hz。

2.1.3 测线上的卫星个数及其PDOP值

图5为各测线上接收的GPS卫星数及其PDOP值，大多数测线上能接收到多于6颗的GPS卫星，不足6颗的测线主要在试验2区第20000～20200线；而PDOP值大多在2.5左右，只有试验1区的10200线和试验2区的20160线出现一时跳跃。

图3 不同采样率下的空间重力异常

图4 不同采样率下的滤波残差对比图

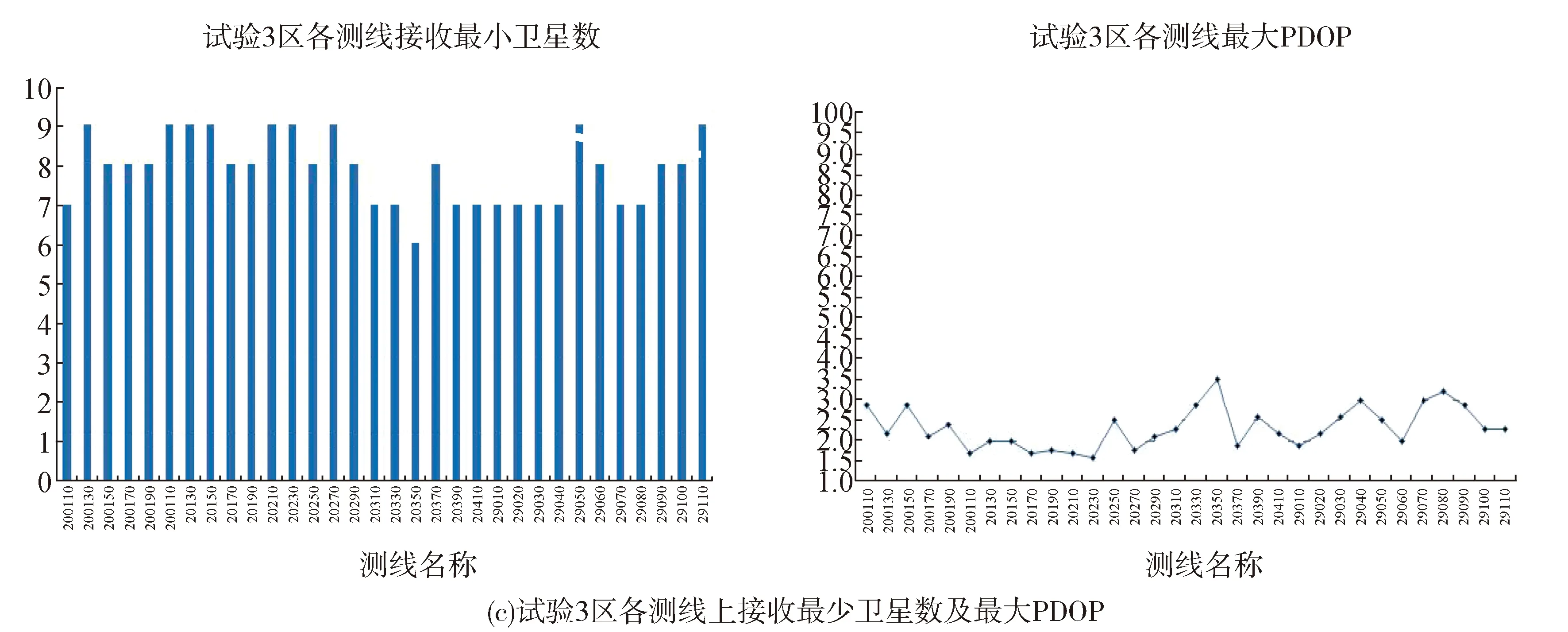
图5 试验区各测线上接收最少卫星数及最大PDOP

处理2区20 000～20 200线发现：20 000～20 200线处理后的残差比其它测线平均高140 mGal(如图6所示)。

对每条测线，计算测线上实时接收到的卫星数及其PDOP值，统计结果如图7所示；而残差值与卫星数之间的统计如图8所示。

根据以上统计可知：接收卫星数与PDOP值正相关，卫星数达到8颗时，PDOP值<2.5，残差最小；当卫星数为6、7或8颗时，残差值最大不超过100 mGal；而当卫星数为5颗时，重力异常残差值达到11 796.56 mGal，超过1 000 mGal。由此可得，在卫星数少于6颗时，航空重力测量成果不可信。因此，航空重力测量中接收卫星数和PDOP是测量成果可靠与否的重要影响因素，测线上务必保持6颗以上的接收卫星数，且PDOP不超过2.5。

图6 试验2区自由重力异常残差图

图7 卫星数量和测线平均PDOP值关系图

图8 残差值与卫星数关系

2.1.4 基线长度

利用5台不同基线长度的基站进行滤波获取自由空间重力异常，其残差见表5。

表5 不同基线长度的滤波残差RMS mGal

由表5可知，当基线长度超过360 km时，自由空间重力异常残差明显超出1 000 mGal；而当基线长度不超过260 km时，明显减小。这表明基线长度对航空重力测量成果产生重要影响，基站离测区越近，残差越小，但200 km以内的基站差异不大。

2.2 姿态影响分析

对3个试验区各条测线的俯仰和翻滚情况进行统计，结果如图9所示。

从图9可知，1、2区测线上的俯仰/翻滚角基本在±5°以内；3区测线的俯仰/翻滚角主要在±10°以内。对3个试验区内的全部测线计算其平均残差，见表6。

表6 试验区平均滤波残差RMS mGal

由表6可知，3区与另外两试验区测线的残差差异较大，且平均残差RMS高达854.61 mGal，明显高于1区和2区的577.59 mGal及547.71 mGal。表明飞行过程中平台姿态角与滤波残差有直接关系。

2.3 重复测线影响分析

重复测线是指航空重力测量中对同一条测线多次飞行，利用重复数据量化精度误差或噪声估计，计算其内符合精度，评价仪器设备的工作性能及稳定性[13-15]。通常计算重复线内符合精度方法的算式为

(6)

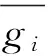
通过对上述公式进行改进，顾及测量过程中测量环境的不定性，进一步消除粗差对测量结果的影响，改进的算式为

(7)

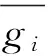
以10条重复测线为算例，对两种计算重复测线内符合精度的方法进行分析与对比，通过传统的方法计算的重复线内符合精度为0.84 mGal，而利用改进后的方法计算重复线内符合精度减小至0.57 mGal，减小幅度达32%。改进后的方法不仅提高重复线内符合精度，也更好的体现仪器的真实状态。

3 结 论

从GPS测量质量、飞机姿态、重复测线内符合精度3个方面对航空重力测量质量的影响因素进行分析，得到如下结论：

1)GPS基站类型对航空重力测量结果有一定影响；基站的采样间隔应选择0.5 s；测线上接收卫星数至少6颗且其PDOP值小于2.5；基站和流动站的基线平均长度不应大于260 km。

2)测量中，确保测线上翻滚/俯仰角应保持在5°以内。

3)顾及测量环境，改进后的内符合精度计算方法可获得更理想可靠的计算结果。

[1] 孙中苗，翟振和，李迎春.航空重力仪发展现状和趋势[J].地球物理学进展，2013,28(1)：01-08.

[2] 孙中苗.航空重力测量理论、方法及应用研究[D].郑州:信息工程大学,2004.

[3] 孙军峰,朱命琪.航空重力测量中基准站与测线的距离对精度的影响[J].测绘地理信息,2014,39(1)：40-42.

[4] 高新兵.航空重力数据处理及其应用研究[D].郑州:信息工程大学,2013.

[5] 冯淑萍,高延民.航空重力数据向下延拓的迭代Tikhonov正则化法[J].地理空间信息,2016,14(10):53-55.

[6] 孙中苗，翟振和，李迎春.航空重力测量的分辨率和精度分析[J].地球物理学进展，2010,25(3)：795-798.

[7] 孙中苗，夏哲仁，王兴涛，等.平原地区航空重力测量的精度分析[J].测绘通报，2006(10)：1-4.

[8] 田颜锋,刘晓刚,孙文,等.航空重力测量中的厄特弗斯改正[J].测绘工程,2011,20(3):9-11.

[9] 张虹.航空重力内符合精度评估方法[J].北京信息科技大学学报，2012,27(2)：01-05.

[10] 姜作喜，张虹，郭志宏，等.航空重力测量内符合精度计算方法[J].物探与化探，2010,34(5)：672-676.

[11] 周波阳,罗志才,钟波，等.航空重力测量的数据归算方法[J].大地测量与地球动力学,2015,35(2):336-341.

[12] 郭志宏，熊盛青，周坚鑫，等.航空重力重复线测试数据质量评价方法研究[J].地球物理学报，2008,51(5)：1538-1543.

[13] 肖凡,孙军峰,王丽红.航空重力测量副测线间距对测量精度的影响[J].地理空间信息,2014(5):122-123.

[14] 谢军,黄建业.航空重力测量的滤波处理及最佳波长分辨率的探讨[J].测绘工程,2001，10(3):35-37.

[15] 张永明,张贵宾,盛军.航空重力梯度测量技术及应用[J].工程地球物理学报,2011,40(6):375-380.