质量比和阻尼比对高阻尼涡激振动的影响

李小超 ， 周熙林 ， 赵利平 ，2

（1.长沙理工大学 水利工程学院，长沙 410004；2.水沙科学与水灾害防治湖南省重点实验室，长沙 410004；3.可再生能源电力技术湖南省重点实验室（长沙理工大学），长沙 410004）

0 引 言

流体流经钝体结构表面时会发生旋涡脱落，当旋涡脱落频率与结构自振频率较为接近时，旋涡脱落频率在一个较大的流速范围内被锁定在结构的自振频率附近，称为频率锁定或同步，此时，结构处于共振状态，共振的结果是使结构产生大振幅振动，此现象称为涡激振动。涡激振动会使很多领域的工程结构遭受严重的破坏[1-2]，如航空航天工程（飞机操纵面）、海洋工程（海底管线、立管、张力腿、采油平台等）和土木工程（桥梁、塔楼、旗杆）等，一直以来，人们努力试图干扰涡旋脱落，抑制涡激振动以防止其对工程结构的破坏。尽管如此，近年来的很多研究[3-5]表明此振动是可利用的，可以利用它从周围流场中提取水流动能，并转化为电能。传统水力发电的方法是使用水轮机，需要平均流速为2.5～3.6 m/s或更高的流速才能发挥较好的效益[6]，而涡激振动水生能源技术可使用仅为0.514 m/s的流速提取高密度能量[3]，因而能够广泛应用于河流、海洋、潮汐和其他水流上。涡激振动水生能源除了可以用来发电之外，也可直接转换成其他形式的可利用机械能，如利用其进行水力抽水或对海水加压脱盐等。Bernitsas等人[3]将涡激振动水生能源的成本费用与其他各种能源的进行了比较（图1），展示出涡激振动水生能源较强的市场竞争力。

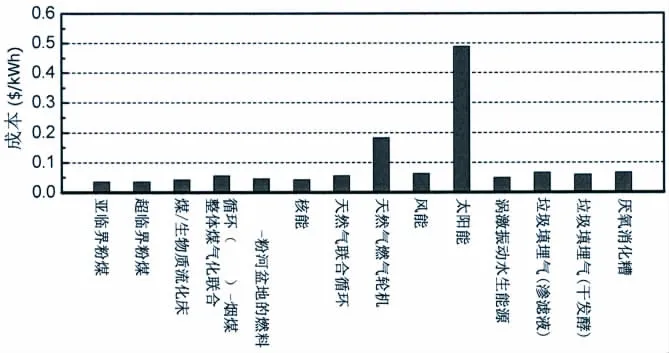
图1 其他能源与涡激振动水生能源关于成本的比较[3]Fig.1 Cost comparison among conventional and alternative sources of energy and the VIV based energy source

涡激振动能量转换装置涉及弹簧支撑的刚性圆柱的涡激振动，见图2。涡激振动是旋涡脱落引起的结果，交互式涡旋脱落产生不对称的振荡升力，使圆柱在垂直于自身轴向和水流流向的方向上振动。涡激振动在圆柱振动方向上产生一个负的阻力，因此圆柱发生涡激振动时从流体中吸取能量。振动体产生的能量取决于振幅和频率，为了使能量输出最大化，必须使系统在频率锁定的条件下运行。频率锁定发生在旋涡脱落频率与结构自振频率较为接近时，并且在一个较大的流速范围内旋涡脱落频率被锁定在结构的自振频率附近，而不仅仅只发生在结构的自振频率上，频率锁定的流速范围是研究关注的重点之一。圆柱振动的振幅是自限制的，其最大响应幅值并不发生在旋涡脱落频率与结构自振频率相等时。上述特性表明，涡激振动是一种自激非线性共振现象。基于振动体的其他海洋能转换装置，如浮筒、水柱、振动板等都是利用线性共振，使振幅达到最大。线性共振的大振幅振动频率带宽较窄。涡激振动能量转换装置是基于非线性共振，在增加转换能量的同时，尽可能地将振动在整个非线性共振范围内与其自限制振幅接近。以往的研究[7-8]表明，质量比对频率锁定的发生以及锁定流速范围有重要的影响。质量比m*定义为振动结构质量与结构排开流体质量之间的比值

图2 单圆柱涡激振动能量转换装置示意图Fig.2 Simple schematic of a VIV based energy converter module

其中：md为结构排开流体质量，对于圆柱体，排水质量为流体密度，D 为圆柱外径，L为圆柱长度。

涡激振动能量转换装置中，通过能量传递系统将圆柱发生涡激振动时的机械能传输到能量转换系统，然后将其转化成电能或其他形式的可利用能源。不管最终的能量形式如何，能量传递和转换会对涡激振动系统引入机械阻尼，高阻尼的引入使得涡激振动能量转换装置不同于一般的涡激振动系统。阻尼太大会抑制涡激振动，导致能量提取失败。阻尼太小会导致能量提取过少。为了获得最优的能量提取，需要对涡激振动系统的阻尼量进行优化。对于涡激振动能量转换装置，系统阻尼包括圆柱—弹簧系统内部阻尼cs、能量传递过程中引起的阻尼ctra、发电机内部电枢的电阻损耗引起的阻尼cgen以及用于能量提取的负载电阻产生的阻尼charn，即c=cs+ctra+cgen+charn，对应的阻尼比定义为

ω为自振频率（圆频率）。

关于质量比和阻尼比对涡激振动的影响，文献[7-9]对其进行了探讨，但都关注于低阻尼情况下的涡激振动，本文将主要探讨高阻尼条件下质量比和阻尼比等参数对涡激振动响应及能量转换效率的影响。

1 数学模型

1.1 模型建立

在流体力的作用下由圆柱、弹簧及能量传递部件（比如齿条）构成的系统结构作为一个整体在竖直方向上下振动，振动位移用y表示，圆柱运动采用二阶方程模拟：

其中：mosc为振动系统质量，包括圆柱质量、能量传递过程中连带振动的部件质量以及弹簧的有效质量，弹簧的有效质量为弹簧总质量的三分之一，k为弹簧刚度，c为系统阻尼系数，ma为附加质量，F为y方向上作用在圆柱体上的流体升力。

圆柱的附加质量可利用附加质量系数由下式计算得到：

其中：Ca为附加质量系数。由于发生频率锁定时，结构处于共振状态，因此结构的响应频率实质上是考虑附加质量后结构的自振频率，响应频率f可由下式计算：

当系统处于共振状态时，系统振动接近于正弦。假定圆柱的振动响应和升力是简谐的，它们的频率同为f，响应和升力之间存在一个相位差。响应y（t）和升力F（t）可以表示为：

其中：A为响应幅值，U为水流流速，CL为升力系数，φ为相位差。Gopalkrishnan[10]通过圆柱受迫振动实验得到的附加质量系数和升力系数，其中附加质量系数与圆柱加速度同相，升力系数与速度同相，φ可取为（速度与位移之间的相位差为）。 于是（7）式变为

将（6）式和（8）式代入（3）式，得响应幅值

在一个振动周期内流体对圆柱做的功可以由升力与位移响应的乘积在一个周期内积分得到。因此，响应y和升力F一旦求出，流体对圆柱做的功可由下式计算：

1.2 模型求解

Gopalkrishnan测得的大部分附加质量系数曲线都几乎垂直于代表无量纲振幅的横坐标轴，这表明附加质量系数对于无量纲振幅的依赖性非常弱，因而可对其进行简化。图3为计算采用的附加质量系数曲线，给出了附加质量系数Ca与无量纲频率f*之间的关系，其数据主要取自Gopalkrishnan测得的附加质量系数图中无量纲振幅A/D=0.5所对应的附加质量系数，该附加质量系数曲线与振幅无关。

从以上分析可知（3）式中附加质量ma、升力F均依赖于响应频率f，而f依赖于附加质量的确定，进而依赖于附加质量系数。为了求解结构响应，我们首先根据附加质量系数曲线确定响应频率f。采用如下计算过程来计算响应频率：

图3 附加质量系数曲线[11]Fig.3 Added mass coefficient curve

（1） 取静水附加质量系数 Ca0=1.0，代入（4）式得静水附加质量ma0，将静水附加质量代入（5）式可得到静水自振频率f0；

（2）选取静水自振频率作为初始响应频率，即fj=0=f0，j为迭代步；计算无量纲频率St为Strouhal数，表征了旋涡脱落频率与流速之间的关为旋涡脱落频率，表示考虑真实Strouhal数对无量纲频率的修正，StG为Gopalkrishnan实验的Strouhal数，StG=0.193，Strouhal数与雷诺数Re有关，雷诺数定义为惯性力与粘滞力的比值，即为流体运动粘滞系数。St由图4所示的

Strouhal数St与雷诺数Re关系曲线得到；

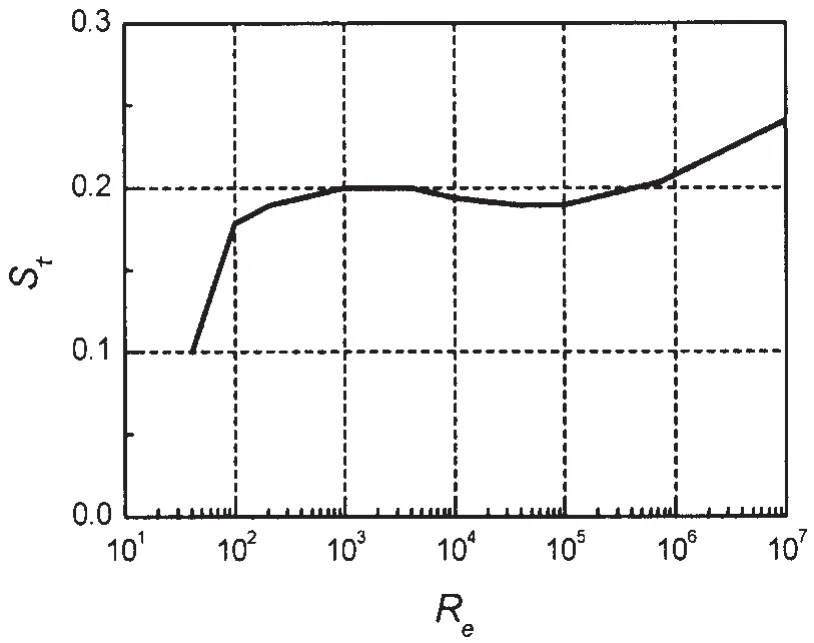
图4 St-Re关系曲线[11]Fig.4 St-Re relationship curve

（3）从图3的附加质量系数曲线中找到上一步得到的无量纲频率对应的附加质量系数，由（4）式计算圆柱附加质量，求得附加质量后代入（5）式，求解得到新的响应频率fj+1；

求得响应频率f之后，可计算对应的无量纲频率f*，此时升力系数CL只是无量纲振幅A/D的函数。图5为升力系数模型，升力系数曲线由AB和BC两段二次曲线构成，B点为最大值点，A、B、C三点的坐标由四个参数CL,max、CL,A/D=0、A/DCL=max以及A/DCL=0确定，它们都是无量纲频率的函数，见图6，其值主要来源于Gopalkrishnan的实验数据。因此，当响应频率确定之后，得到相应的无量纲频率，进而确定参数CL,max、CL,A/D=0、A/DCL=max以及A/DCL=0，从而升力曲线也就确定了。

图5 升力系数模型Fig.5 The lift coefficient model

图6 用于确定升力系数曲线的参数曲线[11]Fig.6 The lift coefficient parameter curves

考虑到升力系数CL依赖于结构的响应幅值，在求解响应幅值A时需要进行迭代，计算采用如下方式：无量纲响应幅值A/D在0到1.0的范围内以0.001的步长逐渐增加直至（5）式满足为止。每一步均需要根据无量纲幅值Aj/D，j为迭代步，由升力系数曲线得到升力系数CL,j，响应幅值由（9）式确定，当满足精度要求时迭代过程停止，接受Aj和CL,j为最终的响应幅值A和升力系数CL。

将求得的响应频率f、响应幅值A和升力系数CL代入（11）式和（13）式即可得到吸收功率Pviv和转换效率η。

1.3 模型验证

基于上述数学模型编制了计算机程序，为了验证程序的正确性，将程序计算结果与Khalak和Williamson[7]的试验结果进行了比较，见图7，图中采用自振频率及圆柱直径分别对响应频率和响应幅值进行了无量纲化。Khalak和Williamson的试验模型具有低质量—阻尼特性，其质量比m*=2.4，阻尼比ζ=0.004 5。从图7可以看出，响应频率的计算结果与试验结果符合得较好，响应幅值的计算结果在无量纲流速U*＜6和U*＞10的范围内与试验结果符合得较好，在6＜U*＜10的范围内较试验结果大。

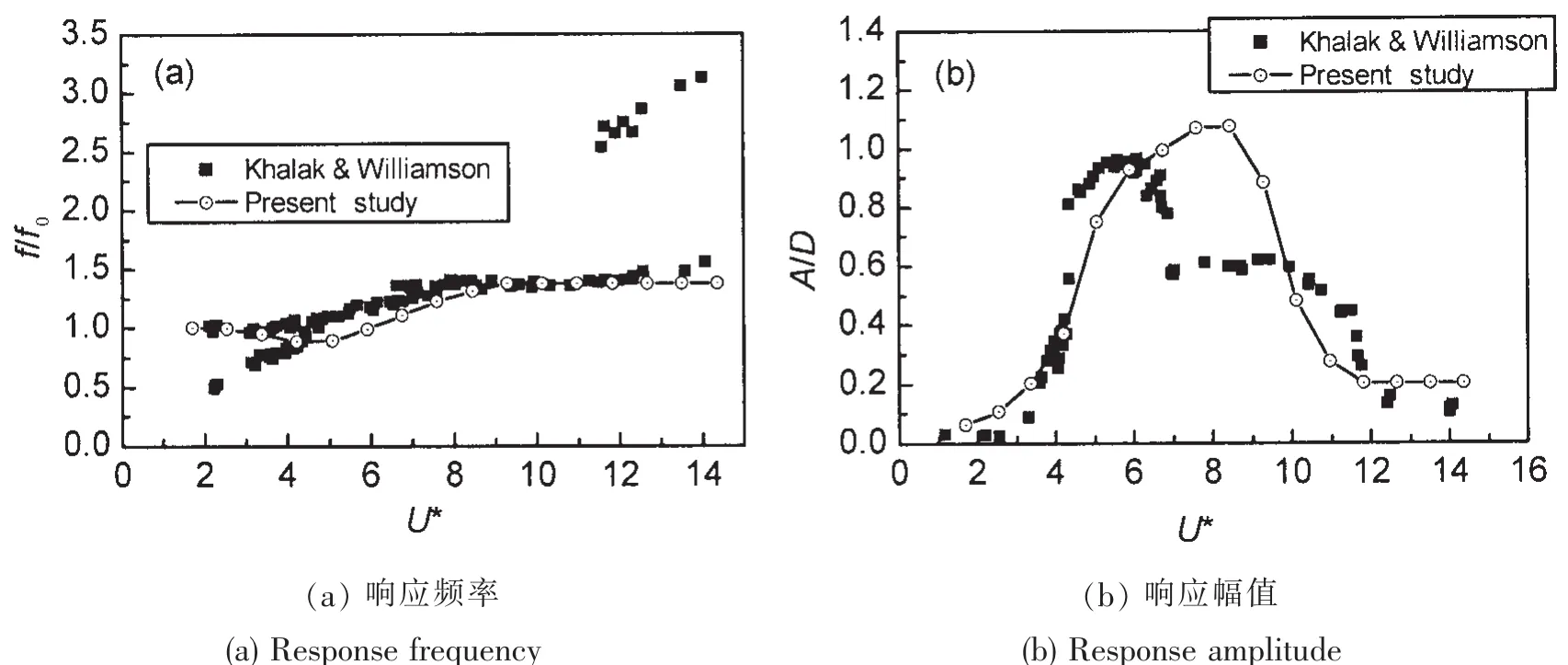
图7 计算结果与Khalak和Williamson试验结果的比较Fig.7 Comparison between calculated and Khalak&Williamson’s experimental results

2 结果分析

2.1 质量比的影响

取直径D=1.0 m，长度L=20.0 m的圆柱进行计算，计算时对弹簧刚度进行调整，使锁定流速范围在0～1.5 m/s以内，下文主要考察质量比和阻尼比对转换效率、锁定范围、无量纲幅值及频率比（响应频率与静水自振频率的比值）的影响。

图8～10分别给出了同一阻尼比下具有四种不同质量比的圆柱无量纲幅值、频率比及能量转换效率随无量纲流速的变化情况。从图8和图10可以看出，无量纲幅值和能量转换效率均随流速的增大先增大后减小，中间存在一个最大值，但两者最大值并不出现在同一无量纲流速下。最大无量纲幅值随质量比的增加而减小，最大能量转换效率随着质量比的增加先增大后减小，两者对应的无量纲流速均往右发生了偏移，表明在保持其他条件不变情况下对于较大质量比圆柱产生最大能量转换效率所需要的流速更大。对于各质量比，频率锁定发生的无量纲流速较为接近，均在4.5附近，频率锁定的发生伴随着无量纲幅值和转换效率的大幅度增加，随着质量比的增加其变化趋势变得平缓。频率锁定结束时的无量纲流速主要在8～12这个范围。锁定范围及较大能量转换效率覆盖的无量纲流速范围随质量比的增加而缩小。由图9可以看出，频率比在锁定范围内随流速的增加而线性增加，并且四种质量比条件下频率比曲线基本重叠在了一起，锁定结束后基本保持不变，其值为最大频率比值，从不同质量比条件下最大频率比的差值来看，质量比在小于5时对频率比的影响更大，质量比为5和8时的最大频率比值较为接近。

图8 不同质量比情况下无量纲幅值随无量纲流速的变化Fig.8 Response amplitude versus nondimensional velocity for varying mass ratios

图9 不同质量比情况下频率比随无量纲流速的变化Fig.9 Response frequency ratio versus nondimensional velocity for varying mass ratios

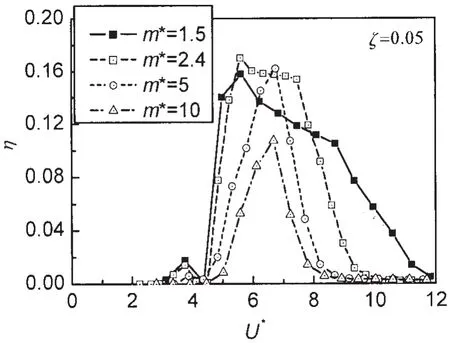
图10 不同质量比情况下能量转换效率随无量纲流速的变化Fig.10 Energy efficiency versus nondimensional velocity for varying mass ratios

2.2 阻尼比的影响

图11和图12分别给出了不同阻尼比条件下具有质量比m*=2.4的圆柱涡激振动能量转换效率和无量纲幅值随无量纲流速的变化曲线，其变化规律与图8和图10相似。最大无量纲幅值随阻尼比的增加而减小，这与Khalak和Williamson[8]的试验结果较为一致，最大无量纲幅值均出现在7.5左右的无量纲流速下。最大能量转换效率随着阻尼比的增加先增大后减小，最大能量转换效率对应的无量纲流速向右发生了偏移，表明在保持其他条件不变情况下对于较大阻尼比圆柱产生最大能量转换效率所需要的流速更大。对于频率锁定的发生，除ζ=0.015时发生无量纲流速为3.0附近之外，其他阻尼比情形均发生在无量纲流速为4.5附近，随着阻尼比的增加，频率锁定发生时无量纲幅值和能量转换效率的增加趋势变得平缓。各阻尼比条件下频率锁定结束时的无量纲流速较为一致，均在9.0附近，表明锁定流速范围受阻尼比的影响较小。

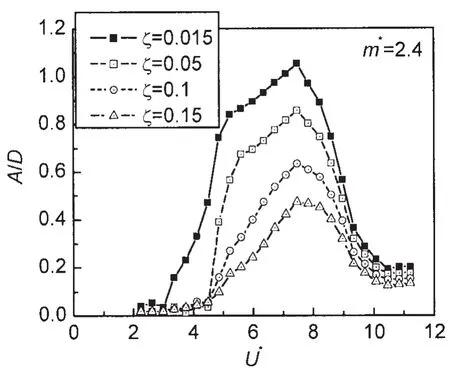
图11 不同阻尼比情况下无量纲幅值随无量纲流速的变化Fig.11 Response amplitude versus nondimensional velocity for varying damping ratio

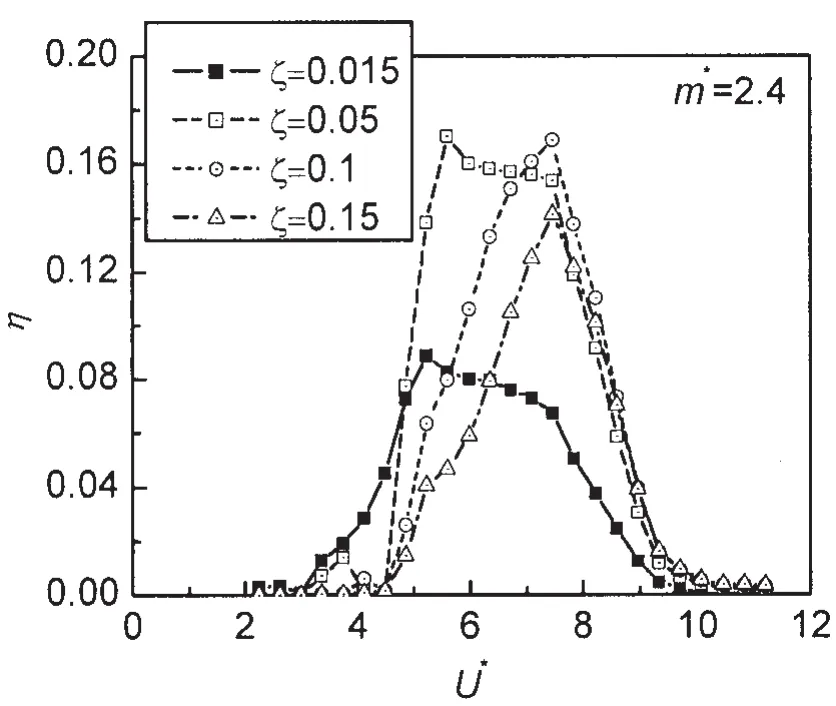
图12 不同阻尼比情况下能量转换效率比随无量纲流速的变化Fig.12 Energy efficiency versus nondimensional velocity for varying damping ratio

2.3 关于质量—阻尼参数

从以上分析可以看出，频率锁定的发生及锁定流速范围主要取决于质量比，而最大能量转换效率以及出现最大能量转换效率的无量纲流速则与质量比和阻尼比均有重要的关系。因此，我们联想到了很多涡激振动研究文献中提到的质量—阻尼联合参数，它是质量比和阻尼比的乘积，即m*ζ。图13和图14分别给出了最大能量转换效率以及出现最大能量转换效率的无量纲流速随质量—阻尼参数m*ζ的变化关系。图13中四条曲线分别对应不同的质量比，每条曲线表现出两个极大值，一个出现在m*ζ=0.1附近，一个出现在m*ζ=0.2附近。尽管不同的质量比情形四条曲线存在差别，但四条曲线非常接近，最大能量转换效率主要取决于质量-阻尼参数，并且存在最优值，其值约为0.1，此时的最大能量转换效率约为0.19，m*ζ=0.2处的最大能量转换效率约为0.17。最大能量转换效率大于0.1的m*ζ范围集中在0.05～0.6内。从图14可以看出，在m*ζ＜0.2的范围内出现最大能量转换效率的无量纲流速随阻尼比的变化而变化，而在0.2＜m*ζ＜0.7的范围内，其值保持不变，表明出现最大能量转换效率的无量纲流速在m*ζ＜0.2的范围内主要取决于m*ζ，而在0.2＜m*ζ＜0.7的范围内其值与阻尼比无关，主要取决于质量比。

图13 最大能量转换效率随质量—阻尼参数的变化Fig.13 Dependence of the maximum efficiency with the mass-damping parameter

图14 出现最大能量转换效率的无量纲流速值随质量—阻尼参数的变化Fig.14 Dependence of the dimensionless velocity where the maximum efficiency appears with the massdamping parameter

3 结 论

基于受迫振动试验结果建立一个单自由度涡激振动分析模型，用于分析涡激振动响应和能量转换效率，考察了质量比和阻尼比等重要参数对涡激振动响应和能量转换效率的影响，结果表明：（1）频率锁定的发生及锁定流速范围主要取决于质量比；（2）最大能量转换效率主要受质量—阻尼参数m*ζ控制，并且存在一个最优值。（3）出现最大能量转换效率的无量纲流速与m*ζ有关，在m*ζ＜0.2的范围内出现最大能量转换效率的无量纲流速随质量比和阻尼比的变化而变化，而在0.2＜m*ζ＜0.7的范围内与阻尼比无关，主要取决于质量比。本文的涡激振动模型采用的流体力数据主要来源于受迫振动试验结果，目前关于是否可以用受迫振动试验数据来预报涡激振动还在争论当中，尽管如此，Morse和Williamson[12]的研究结果表明，在合适的控制条件下，自由振动实验和受迫振动实验可以得到非常一致的结果，因此本文结果可作为现实情况的一种近似。涡激振动是一个非常复杂的流固耦合问题，其影响参数众多，很多参数的影响有待进一步研究，希望本文的研究对涡激振动能量转换装置的设计及未来的实验研究有所帮助。

[1]Sarpkaya T.A critical review of the intrinsic nature of vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(4):389-447.

[2]Williamson C H K,Govardhan R.A brief review of recent results in vortex-induced vibrations[J].Journal of Wind Engineering and Industrial Aerodynamics,2008,96(6-7):713-735.

[3]Bernitsas M M,Raghavan K,Ben-Simon Y,Garcia E M H.VIVACE(Vortex Induced Vibration Aquatic Clean Energy):A new concept in generation of clean and renewable energy from fluid flow[J].Journal of Offshore Mechanics and Arctic Engineering,2008,130(4):041101-1-041101-15.

[4]Abdelkefi A,Hajj M R,Nayfeh A H.Phenomena and modeling of piezoelectric energy harvesting from freely oscillating cylinders[J].Nonlinear Dynamics,2012,70(2):1377-1388.

[5]Nishi Y.Power extraction from vortex-induced vibration of dual mass system[J].Journal of Sound and Vibration,2013,332(1):199-212.

[6]Bedard R,Previsic M,Siddiqui O,Hagerman G,Robinson M.Tidal in Stream Energy Conversion(TISEC)Devices[R].Palo Alto,California:Electric Power Research Institute,2005.EPRI-TP-004NA.

[7]Khalak A,Williamson C H K.Fluid forces and dynamics of a hydroelastic structure with very low mass and damping[J].Journal of Fluids and Structures,1997,11(8):973-982.

[8]Khalak A,Williamson C H K.Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,71:341-350.

[9]Bahmani M H,Akbari M H.Effects of mass and damping ratios on VIV of a circular cylinder[J].Ocean Engineering,2010,37(5-6):511-519.

[10]Gopalkrishnan R.Vortex-induced forces on oscillating bluff cylinders[D].Cambrige:Massachusetts Institute of Technology,1993.

[11]Larsen C M,Vikestad K,Yttervik R,Passano E.Empirical model for analysis of vortex induced vibrations-theoretical background and case studies[C]//20th International Conference on Offshore Mechanics and Arctic Engineering.Rio de Janeiro,2001.

[12]Morse T L,Williamson C H K.Prediction of vortex-induced vibration response by employing controlled motion[J].Journal of Fluid Mechanics,2009,634:5-39.