轴压复合材料蛋形壳屈曲特性

周 通 ， 唐文献 ， 王纬波 ， 张 建 ，

（1.江苏科技大学 机械工程学院，江苏 镇江 212003；2.中国船舶科学研究中心 船舶振动噪声国家重点实验室，江苏 无锡 214082；3.南京航空航天大学 机电学院，南京 210016）

0 引 言

随着陆地矿产资源的逐渐枯竭，人类将石油、天然气的开采转向海洋。海洋石油钻井平台是获取海底资源的重要装置。海洋平台的桩腿支撑着整个平台的重量，同时受到洋流与风浪的影响，桩腿的承载能力与可靠程度决定着整个平台的性能与稳定性。CFRP（Carbon Fiber Reinforced Plastics）型复合材料具有比强度高、比刚度大、抗疲劳与耐腐蚀性强等特点，已逐渐取代传统金属材料被广泛应用于航海、航空、航天等领域[1]。

根据欧洲标准EN 1993-1-6[2]，张建等[3]通过引入多模态缺陷的方法，研究了轴压复合材料柱形壳屈曲特性，发现第1阶模态缺陷不一定是最差缺陷，屈曲载荷下降受缺陷形状、幅值双重影响。复合材料柱形壳是具有相近空间特征值的缺陷敏感性结构，在轴压工况下，其失稳破坏最先发生在中部区域。为了在不改变壳体整体性的前提下提高其轴向承载能力，除了改变柱形壳的长细比L/R，还可以通过改变壳体侧壁形状对其进行优化设计。当壳体承受均布外压时，最理想的形状应该是球形壳体，球壳可以承受较大的均布外压。但是，球形壳体对于缺陷较为敏感且加工难度大，很小的初始缺陷都会造成屈曲临界载荷的极度下降。Jasion等[4-5]将球形壳与柱形壳进行组合，研究不同形状桶形壳的线弹性屈曲失稳模式。虽然桶形壳省去了柱形壳中部的加强肋板，但是，桶形壳的母线仍为对称结构，不可避免的带来了缺陷敏感性问题。Blachut等[6-8]研究了轴压与均布侧压组合条件下复合材料柱形壳与桶形壳的线弹性屈曲特性，并分析了边界条件与初始几何缺陷对其影响。蛋形壳体结构不同于球形壳、柱形壳、桶形壳，初始缺陷对其承载能力影响较小，既具有桶形壳的无肋特征，又具有柱形壳轴向承载能力较高的优势，且可以像球形壳一样承受较大的均布外压。蛋壳是一种满足正高斯曲线的多焦点、回转型薄壁结构，具有良好的重量强度比、跨距厚度比、流线型、美学特性、合理的材料分布等优点；蛋壳满足圆顶原理，无须额外肋骨支撑，利用最少材料即可获得足够的强度和稳定性；在均布压力作用下，蛋壳可通过面内压力抵抗外载荷，表现出超强的耐压特性。蛋壳所呈现的这些优异生物特性，是其尺寸、形状、厚度、材料等因素协同作用的结果，这些因素相互依存、相互影响。显然，蛋壳作为一种优异的设计原型，可为耐压壳的设计提供有效的生物信息[9]。蛋形壳体具有抗压能力强、壳内空间利用率高、水动力学特性好等优点，便于开孔与开窗，且在低频阶段具有良好的声学特性，在海洋装备结构上具有广阔的应用前景[10-12]。

Liang等[13]将无肋结构球形壳进行交接，对多球交接形壳体进行优化设计，并得到连接法兰合理的形状与尺寸。Iwicki等[14]通过敏感性分析的方法研究了不同形式的加强肋对柱形壳承载能力的影响。Ross等[15]采用环氧树脂粘合剂将固体聚氨酯塑料的扁球形封头与多个按一定顺序排列的法兰粘结，研究了法兰对复合材料壳体加强的影响。Muljowidodo等[16]采用模块化的方法设计复合材料交接形壳体，模块化的交接形壳体便于安装与维护。Blachut等[17-18]在研究复合材料桶形壳屈曲特性时，将多个桶形壳通过法兰连接首尾串接，研究其轴压屈曲特性。

本文基于模态缺陷条件下轴压复合材料柱形壳屈曲特性研究，结合以K函数表示的蛋形曲线，运用等质量与等容积两种方法，对柱形壳进行形状优化设计。引入5%缺陷幅值的模态缺陷，研究复合材料蛋形壳的轴压屈曲特性。从工程实例出发，以单立柱固定式平台的柱形壳桩腿为例，采用分段式模块化设计的方法，对比一般钢结构柱形壳桩腿、CFRP复合材料柱形壳桩腿和CFRP复合材料多蛋交接形桩腿，研究5%多模态缺陷条件下三种桩腿的轴压屈曲特性。

1 问题描述

以单立柱固定式海洋平台柱形壳桩腿为研究背景，结合轴压复合材料柱形壳屈曲特性的研究方法，设计复合材料蛋形壳，对其进行线弹性与非线性屈曲分析。复合材料柱形壳的内直径为140 mm，长度为170 mm（去除两端加强围栏后135 mm）；柱形壳由四层碳纤维铺设而成，每层纤维厚度为0.111 mm，共 0.444 mm；四层碳纤维由环氧树脂粘合，铺层角为[0°/45°/-45°/0°]。 制作柱形壳与蛋形壳的材料均为CFRP环氧树脂基碳纤维复合材料，其属性如表1所示，其中tc为单层纤维厚度，n为铺层数，本文所研究复合材料柱形壳tc为0.111mm，n为4。

表1 CFRP层合板型复合材料的材料属性Tab.1 Material properties of the CFRP composite laminate ply

对于轴压复合材料柱形壳试验模型，由经典层合壳理论、轴向压缩试验得到其屈曲临界载荷解析解与试验值分别为27.11 kN、19.41 kN。通过网格收敛性检查，选取2×2 mm的S4R壳单元对柱形壳进行网格划分，并对复合材料柱形壳进行轴压线弹性屈曲分析，得到前50阶屈曲临界载荷与失稳模式。其中，1阶屈曲特征值为27.45 kN，与解析解27.11 kN相差1.25%。通过三维扫描试验，得到柱形壳的初始几何缺陷为0.022 2 mm，相对柱形壳厚度0.444 mm，即为5%的缺陷幅值。将50阶线弹性屈曲失稳模式设置为初始缺陷，并引入几何非线性，在5%缺陷幅值条件下对轴压复合材料柱形壳进行非线性屈曲分析，得到的衰减系数（KDF，Knock-down Factor）曲线如图6所示。结果表明，第1阶屈曲模态缺陷并非最差缺陷，临界载荷为21.30 kN，与试验值19.41 kN的误差高达9.74%；第18阶模态缺陷为最差缺陷，屈曲载荷19.65 kN与试验值19.41 kN的误差仅为1.24%。其中，5%缺陷幅值第18阶模态缺陷条件下，轴压复合材料柱形壳载荷—位移曲线如图7所示。复合材料柱形壳是具有相近空间特征值的缺陷敏感性结构，在对其进行铺层优化与尺寸优化的基础上，本文结合仿生学原理，运用蛋形结构对柱形壳进行形状优化。

2 数学模型

2.1 蛋形壳几何模型

2.1.1 蛋形曲线方程

蛋壳外形是以正高斯曲线为母线旋转而成的多焦点曲面，其表面每一点在经线和纬线方向都有两个曲率半径，每个曲率半径代表一小段圆弧，两段圆弧相互垂直。不同鸟类、禽类的蛋壳形状存在差异，一般采用形状特征参数和形状函数来描述其几何特征。其中，蛋壳形状特征参数包括：长轴、短轴、中径、圆球度、表面积、体积、形状系数、延伸率、厚度、厚度系数等，这些特征参数之间存在近似的数学关系。

在笛卡尔坐标系下，采用K函数对复合材料蛋形壳曲线进行拟合。如图1所示，以K函数表示的蛋形壳母线，蛋形曲线长短轴交点为坐标系原点O，长轴为x轴，方向由小端指向大端，短轴为y轴。

图1 以K函数表示的蛋形壳曲线Fig.1 Egg-shaped curve based on K-function

蛋形曲线函数采用K函数

对应的参数方程为

其中：L为蛋形壳体的长轴长度，B为蛋形壳体的短轴长度，e为偏心距（L/e=45～55）；蛋形壳体的长轴为x轴，短轴为y轴，原点与蛋形仿生壳体中心相距为e；蛋形系数B/L=0.62～0.76。

与柱形壳相同，采用中面来设计蛋形壳。本文以K函数为蛋形曲线，根据已知的复合材料柱形壳模型来设计复合材料蛋形壳。由大量的鹅蛋形状测量试验[9]，取蛋形系数B/L=0.69，L/e=50。蛋形壳采用两端开孔形式，开孔大小均与已知柱形壳模型直径相同。为了与已知复合材料柱形壳形成对比，分别采用等质量、等容积的方法来设计复合材料蛋形壳，蛋形壳采用与柱形壳相同的环氧树脂基碳纤维复合材料。为了简化计算过程，下文均以壳体中面形状为基准进行设计。

2.1.2 蛋形壳等质量设计方法

等质量的设计方法要求蛋形壳和柱形壳具有相同的质量，对于薄壳结构，可以近似用中面面积相等代替壳体质量相等，且保证两壳体厚度相同。

由蛋形方程（1），可得蛋形壳中面面积为

其中：B/L=0.69，L/e=50。

柱形壳的中面面积为

对于本文所研究的复合材料柱形壳试验样本，中面半径R0=70 mm，L0=135 mm，中面表面积S0=18 900π mm2。

其中：x1、x2为方程（5）的 2 个根，且 x1＜x2。 结合图 1 可知，x1=-L1，x2=L2。

R0为柱形壳中面半径。

为了得到蛋形壳的短轴长度B，需要根据柱形壳半径R0确定蛋形壳短轴长度B的取值范围（B/2＞R0，且B通常需要圆整），以1.1R0作为初始的B/2进行试根。通过预设的短轴长度B解出上述方程（5）的根x1与x2，并将x1与x2代入蛋形壳中面面积S1的计算公式（3）求出S1的值，将蛋形壳中面面积S1与柱形壳中面面积S0进行对比，并进一步缩小B的取值范围，以得到蛋形壳短轴长度B的合理取值。

运用MATLAB求解上述方程与积分。当蛋形壳短轴B=163 mm 时，由方程（5）可得 x1=-61.732 4 mm、x2=59.253 9 mm，蛋形壳中面面积S1=18 821π mm2。从而可得，蛋形壳长轴L=236 mm，e=5 mm。与柱形壳等质量的蛋形壳曲线如图2所示。

图2 等质量复合材料蛋形壳蛋形曲线Fig.2 Egg-shaped curve of the equalmass composite egg-shaped shell

2.1.3 蛋形壳等容积设计方法

等容积的设计方法要求蛋形壳和柱形壳具有相同的容积，对于薄壳结构，用中面来代替壳体，且保证两壳体厚度相同。

由蛋形方程（1），可得蛋形壳的容积为

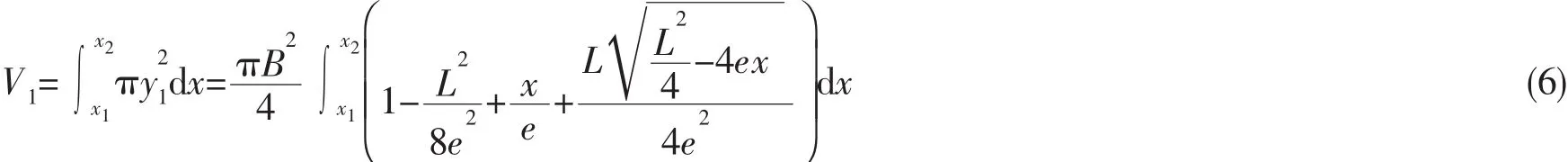
其中：B/L=0.69，L/e=50。

柱形壳的容积为

对于本文所研究的复合材料柱形壳试验样本，中面半径R0=70 mm，L0=135 mm，容积近似以中面表示 V0=661 500π mm3。

其中：x1、x2为以下方程的 2 个根，且 x1＜x2。 结合图 1 可知，x1=-L1，x2=L2。

R0为柱形壳中面半径。

为了得到蛋形壳的短轴长度B，需要根据柱形壳半径R0确定蛋形壳短轴半径B的取值范围（B/2＞R0，且B通常需要圆整），以1.1R0作为初始的B进行试根。通过预设的短轴长度B解出上述方程（8）的根x1与x2，并将x1与x2代入蛋形壳中面容积V1的计算公式（6）求出V1的值，将蛋形壳中面容积V1与柱形壳中面容积V0进行对比，并进一步缩小B的取值范围，以得到蛋形壳短轴长度B的合理取值。

运用MATLAB求解上述方程与积分。当蛋形壳短轴B=160 mm 时，由方程（8）可得x1=-57.217 1 mm、x2=55.043 2 mm，蛋形壳中面容积S1=662 340π mm3。从而可得，蛋形壳长轴L=232 mm，e=5 mm。与柱形壳等容积的蛋形壳曲线如图3所示。

图3 等容积复合材料蛋形壳蛋形曲线Fig.3 Egg-shaped curve of the equal-volume composite egg-shaped shell

2.2 复合材料蛋形壳数值模型

2.2.1 理想复合材料蛋形壳数值模型

蛋形壳采用两端开孔形式，开孔大小均与柱形壳相同。在建立复合材料蛋形壳有限元模型时，采用与柱形壳相同的网格属性、材料参数和边界条件。建立复合材料蛋形壳有限元模型，如图4所示。选取4节点减缩积分壳单元S4R对蛋形壳进行网格划分，等质量蛋形壳模型共包含13 640个S4R减缩积分壳单元与13 860个节点（如图4（a）所示），等容积蛋形壳模型共包含12 540个S4R减缩积分壳单元与 12 760 个节点（如图 4（b）所示）。 蛋形壳各层的纤维排布方式为[0°/45°/-45°/0°]，各层纤维材料的弹性参数与柱形壳保持一致，见表1。结合柱形壳的边界条件，将两端开孔蛋形壳底端（大端）完全固定，顶端（小端）以圆心为参考点采用刚体约束。在参考点施加沿轴线向下的压缩载荷，特征值屈曲分析阶段施加的轴压载荷为1 kN，非线性屈曲分析阶段施加的载荷根据其屈曲特征值确定，保证分析过程中复合材料蛋形壳的可靠失稳。

图4 CFRP复合材料蛋形壳有限元模型Fig.4 FEA models of CFRP composite egg-shaped shells

2.2.2 缺陷复合材料蛋形壳数值模型

结合缺陷复合材料柱形壳有限元模型，建立缺陷复合材料蛋形壳有限元模型。通过对复合材料蛋形壳进行线弹性屈曲分析，分别得到等质量蛋形壳与等容积蛋形壳前50阶屈曲临界载荷和失稳模式，将这些失稳模式设置为初始缺陷，并引入几何非线性。以复合材料蛋形壳前50阶失稳模式为基础，引入5%缺陷幅值的模态缺陷，研究模态缺陷条件下复合材料蛋形壳的轴压屈曲特性。等质量蛋形壳与等容积蛋形壳的厚度均为0.444 mm，对应5%模态缺陷的真实缺陷幅值为0.022 2 mm。运用弧长法对缺陷柱形壳进行分析求解，采用自动增量步，初始弧长增量步为0.1 mm，最小弧长增量步为0.000 01 mm，最大弧长增量步为0.1 mm，最大迭代次数为100。

3 结果分析与讨论

3.1 蛋形壳线弹性屈曲分析结果

分别对与复合材料柱形壳等质量、等容积的复合材料蛋形壳进行线弹性屈曲分析，得到其前50阶屈曲特征值与失稳模式如表2与表3所示。由表2与表3，对于纤维排布为[0°/45°/-45°/0°]的CFRP复合材料蛋形壳，各阶屈曲失稳模式均为波峰与波谷按一定规律交错排列的对称结构。

表2 等质量复合材料蛋形壳前50阶轴压屈曲临界载荷与失稳模式Tab.2 50 eigenvalues and buckling shapes of a equal-mass composite egg-shaped shell under axial compression

表3 等容积复合材料蛋形壳前50阶轴压屈曲临界载荷与失稳模式Tab.3 50 eigenvalues and buckling shapes of a equal-volume composite egg-shaped shell under axial compression

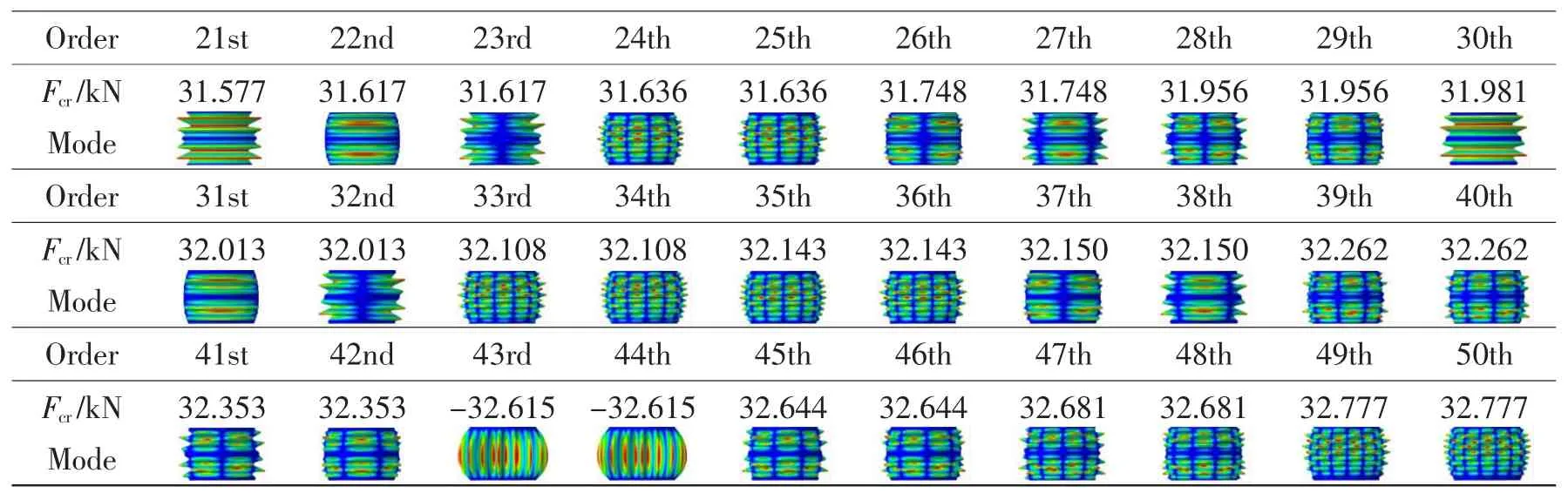
续表3

如表2所示，对于与复合材料柱形壳等质量的复合材料蛋形壳，第1阶屈曲特征值为30.338 kN，第50阶屈曲特征值为32.392 kN，与第1阶屈曲特征值相差6.77%。因为存在多组同根值屈曲模态，所以相邻阶屈曲特征值最小偏差为0。相邻阶屈曲特征值最大偏差为0.89%，存在于第14阶与第15阶之间。

如表3所示，对于与复合材料柱形壳等容积的复合材料蛋形壳，第1阶屈曲特征值为30.493 kN，第50阶屈曲特征值为32.777 kN，与第1阶屈曲特征值相差7.49%。因为存在多组同根值屈曲模态，所以相邻阶屈曲特征值最小偏差为0。相邻阶屈曲特征值最大偏差为1.04%，存在于第18阶与第19阶之间。

等质量复合材料蛋形壳短轴B=163 mm，等容积复合材料蛋形壳短轴B=160 mm。对于第1阶线弹性屈曲特征值，等容积复合材料蛋形壳比等质量复合材料蛋形壳高出0.51%。如图5所示，为等质量复合材料蛋形壳与等容积复合材料蛋形壳的1阶线弹性屈曲失稳模式。屈曲特征值的相邻偏差较小说明复合材料蛋形壳是具有相近分立特征值问题的缺陷敏感性结构，因此，通过引入不同缺陷形状与缺陷幅值的模态缺陷研究蛋形壳的缺陷敏感度具有很深远的意义。

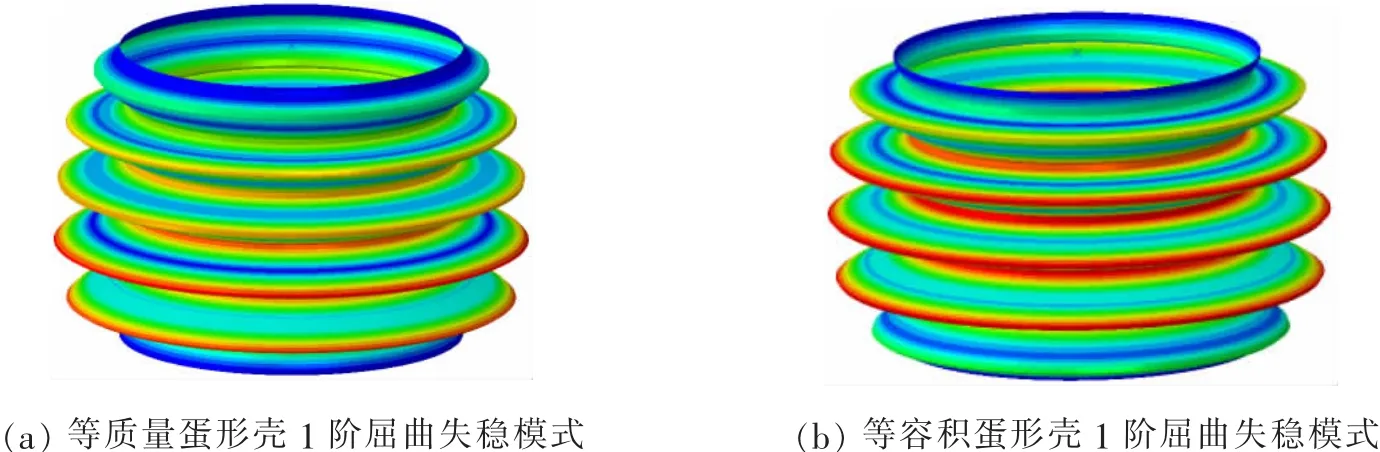
图5 CFRP复合材料蛋形壳1阶线弹性屈曲失稳模式Fig.5 1st linear buckling modes of CFRP composite egg-shaped shells

3.2 蛋形壳非线性屈曲分析结果

在5%缺陷幅值的条件下，得到复合材料柱形壳、等质量复合材料蛋形壳、等容积复合材料蛋形壳的前50阶模态衰减系数曲线，如图6所示。复合材料柱形壳的最差阶缺陷为第18阶，衰减系数为0.716，衰减系数的极差为0.144；等质量复合材料蛋形壳的最差阶缺陷为第11阶与第12阶，衰减系数为0.829，衰减系数的极差为0.152；等容积复合材料蛋形壳的最差阶缺陷为第9阶，衰减系数为0.838，衰减系数的极差为0.154。等质量蛋形壳与等容积蛋形壳的衰减系数曲线均在复合材料柱形壳之上且高出较多，说明缺陷对蛋形壳轴向承载能力的影响远远小于对柱形壳的影响，蛋形壳对缺陷的敏感性较低。等容积蛋形壳相对等质量蛋形壳具有更好的轴向承载能力，更低的缺陷敏感度，对于复合材料柱形壳的形状优化设计具有指导性作用。

图6 轴压复合材料蛋形壳与柱形壳衰减系数曲线Fig.6 Knock-down factors of composite egg-shaped shells and cylindrical shell under axial compression

如图7所示，为5%缺陷幅值的最差阶模态缺陷条件下轴压复合材料柱形壳、等质量与等容积复合材料蛋形壳的载荷-位移曲线。在初始阶段，随着轴向压缩量的增大，轴向压力呈等比例上升趋势，上升速度为柱形壳＞等容积蛋形壳＞等质量蛋形壳。当轴向压缩量为0.39 mm时，复合材料柱形壳的载荷-位移曲线出现拐点，最先发生失稳，轴向压缩载荷急剧下降，屈曲临界载荷为19.65 kN；当轴向压缩量为0.79 mm时，等容积蛋形壳发生失稳，屈曲临界载荷为25.56 kN；当轴向压缩量为0.83 mm时，等质量蛋形壳发生失稳，屈曲临界载荷为25.16 kN。对于非线性屈曲临界载荷，等容积蛋形壳比柱形壳高出30.08%，比等质量蛋形壳高出1.59%。相对于复合材料柱形壳，复合材料蛋形壳会在更大的压缩量下发生失稳破坏，有利于及时发现设备与结构的隐患与故障，提高了结构的安全性与可靠性。

如图8所示，为最差阶模态缺陷、5%缺陷幅值条件下，轴压复合材料蛋形壳屈曲破坏形式。等质量蛋形壳的最差阶模态缺陷为第11阶，最大位移出现在蛋形壳中部偏向小端区域，在环向对称分布三个形状相似的凹陷。等容积蛋形壳的最差阶模态缺陷为第9阶，如果不考虑轴向压缩位移（仅考虑径向位移）则最大位移出现在蛋形壳中部赤道部位，沿环向呈现周期性的凸出与凹陷。

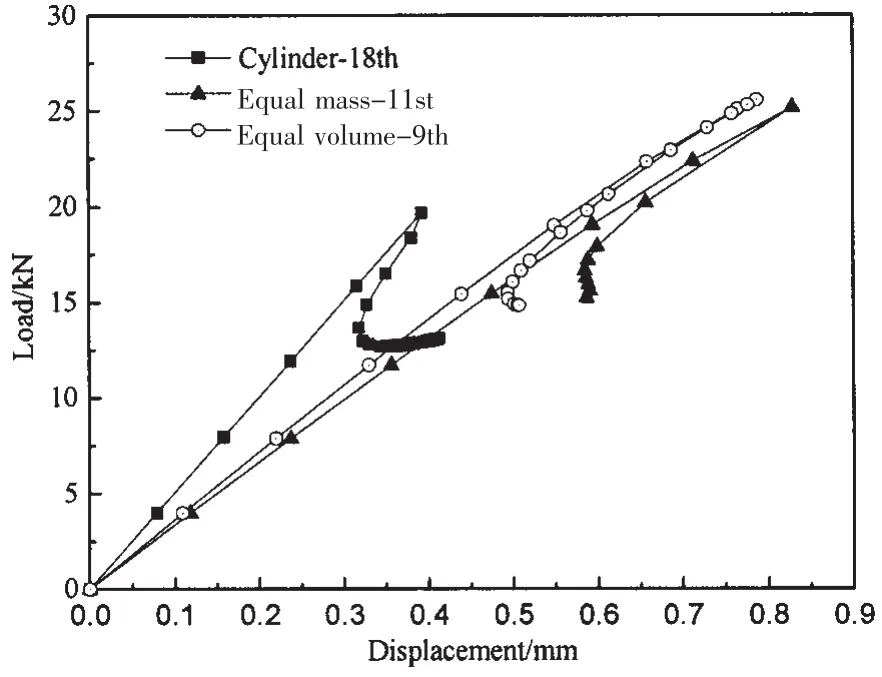
图7 轴压复合材料蛋形壳与柱形壳载荷—位移曲线Fig.7 Load-displacement curves of composite egg-shaped and cylindrical shells under axial compression

图8 轴压缺陷蛋形壳非线性屈曲失稳模式Fig.8 Nonlinear buckling shapes of imperfect egg-shaped shells under axial compression

3.3 单立柱平台桩腿设计分析实例

3.3.1 柱形壳桩腿与多蛋交接形桩腿设计

已知柱形壳桩腿中面直径为7 m，长度为21 m，壳体厚度根据轴压设计载荷45 000 kN并结合线弹性屈曲分析与非线性屈曲分析得出。壳体材料有金属材料 （本文以Q235-A型钢为研究对象）和CFRP复合材料，金属材料仅研究柱形壳桩腿，CFRP复合材料需研究柱形壳桩腿和多蛋交接形桩腿。根据柱形壳桩腿设计多蛋交接形桩腿时，先将柱形壳桩腿等分三段（每段长度均为7 m），根据其中一段柱形壳（直径7 m，长度7 m）由等容积方法设计蛋形壳，将三只相同的蛋形壳串接形成多蛋交接形桩腿。等容积的设计方法要求蛋形壳和柱形壳具有相同的容积，对于薄壳结构，用中面来代替壳体，且保证两壳体厚度相同。

由用K函数表示的蛋形方程（1）得到蛋形壳的容积计算式（6），结合柱形壳的容积计算式（7），运用等容积的设计方法，令蛋形壳与柱形壳的容积相等，得到蛋形壳母线与柱形壳母线的两个交点对应的两个根x1与x2（x1＜x2），蛋形壳的蛋形系数B/L=0.69且L/e=50。对于本文所研究的复合材料柱形壳桩腿，中面半径R0=3.5 m，长度L0=7 m，容积近似以中面表示为V0=85.75π m3。

为了得到蛋形壳的短轴长度B，需要根据柱形壳半径R0确定蛋形壳短轴半径B的取值范围（B/2＞R0，且B通常需要圆整），以1.1R0作为初始的B进行试根。通过预设的短轴长度B解出方程（8）的根x1与x2，并将x1与x2代入蛋形壳中面容积V1的计算公式（6）求出V1的值，将蛋形壳中面容积V1与柱形壳中面容积V0进行对比，并进一步缩小B的取值范围，以得到蛋形壳短轴长度B的合理取值。

运用MATLAB求解上述方程与积分。当蛋形壳短轴B=8 051 mm 时，由方程（8）可得 x1=-2 939.0 mm、x2=2 825.1 mm，蛋形壳中面容积V1=85.807 0π m3。从而可得，蛋形壳长轴L=11 668 mm，偏心距e=233 mm。在对蛋形壳进行串接时，取短轴B=8 050 mm，长轴L=11 670 mm，偏心距 e=230 mm，如图9所示。用直径为7 m的柱形壳截取蛋形壳中间部分，依次首尾串接形成多蛋交接形桩腿，两端连接部分为直径7 m的柱形壳，与蛋形壳大、小端相连的长度分别为1 911 mm、1 800 mm，使整个交接形壳体桩腿的总长度仍为21 m。根据直径7 m、长21 m的柱形壳得到的多蛋交接型桩腿如图10所示。

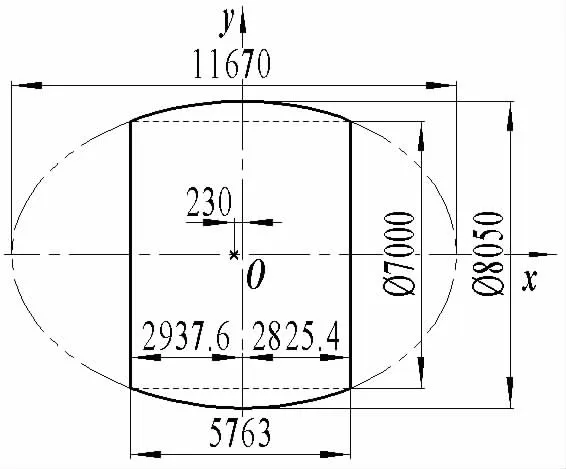
图9 等容积复合材料蛋形壳蛋形曲线Fig.9 Egg-shaped curve of the equal-volume composite egg-shaped shell

图10 复合材料多蛋交接形桩腿Fig.10 Composite multiple intersecting egg-shaped spud leg

3.3.2 海洋平台桩腿数值模型

（1）海洋平台桩腿线弹性数值模型

建立柱形壳桩腿与多蛋交接形桩腿有限元模型，如图11所示，选取4节点减缩积分壳单元S4R对柱形壳桩腿与多蛋交接形桩腿进行网格划分，网格尺寸为200。

如图11（a）所示，柱形壳桩腿包含11 880个S4R壳单元与11 990个节点。将柱壳底端完全固定，顶端以圆心为参考点采用刚体约束，在参考点施加沿轴线向下的压缩载荷。柱形壳均等划分为三段，各段连接处需设置加强肋板与连接法兰，建立有限元模型时，两个连接处一圈的节点仅保留沿轴向移动的自由度。特征值屈曲分析阶段施加的轴压载荷为1 kN，非线性屈曲分析阶段施加的载荷根据其屈曲特征值确定，保证分析过程中柱形壳桩腿的可靠失稳。

图11 海洋平台桩腿有限元模型Fig.11 Spud leg FEA model of ocean platform

如图11（b）所示，多蛋交接形桩腿包含11 872个S4R壳单元与11 984个节点。将最下端蛋形壳与柱形壳连接处完全固定，顶端蛋形壳与柱形壳连接处以圆心为参考点采用刚体约束，在参考点施加沿轴线向下的压缩载荷。蛋形壳连接处需设置加强肋板与连接法兰，建立有限元模型时，两个连接处一圈的节点仅保留沿轴向移动的自由度。特征值屈曲分析阶段施加的轴压载荷为1 kN，非线性屈曲分析阶段施加的载荷根据其线弹性屈曲特征值确定，保证分析过程中复合材料多蛋交接形桩腿的可靠失稳。

金属柱形壳桩腿材料选用Q235-A钢，其弹性模量为2.1e5 MPa，泊松比为0.274，屈服强度为235 MPa，密度为7 860 kg/m3。复合材料柱形壳桩腿与多蛋交接形桩腿依然选用CFRP层合板型复合材料，由基质和增强纤维相互缠绕而成，所研究的柱形壳各层的纤维排布方式为[0°/45°/-45°/0°]，各层纤维材料的力学属性如表1所示。其中，复合材料层合壳体各层厚度tc将在下文给出，层数n为4。有限元分析软件为Abaqus 6.13，使用Abaqus/Standard求解器进行计算。

（2）海洋平台桩腿非线性数值模型

通过对金属柱形壳桩腿、复合材料柱形壳桩腿与多蛋交接形桩腿的轴压线弹性屈曲分析，分别得到三种壳体的前50阶屈曲临界载荷与失稳模式，以这50阶失稳模式为基础，引入5%缺陷幅值的模态缺陷并考虑几何非线性的影响，研究模态缺陷条件下三种海洋平台的轴压屈曲特性。

在研究三种海洋平台桩腿的轴压屈曲特性之前，需要确定各桩腿的厚度。本文根据设计载荷4 500 t，结合5%缺陷幅值1阶模态缺陷条件下三种桩腿的轴压屈曲分析，对一系列的壳体厚度（精度1 mm）进行试算，当非线性轴压屈曲临界载荷恰好大于设计载荷时，即为桩腿合理的设计厚度。最终可得，Q235-A钢柱形壳桩腿厚度为9 mm，对应的5%缺陷幅值为9×0.05=0.45 mm；CFRP复合材料柱形壳桩腿的厚度为20 mm（共4层，每层5 mm），对应的5%缺陷幅值为20×0.05=1 mm；多蛋交接形桩腿厚度为20 mm（共4层，每层5 mm），对应的5%缺陷幅值为20×0.05=1 mm。运用弧长法对缺陷柱形壳进行分析求解，采用自动增量步，初始弧长增量步为0.1 mm，最小弧长增量步为0.000 01 mm，最大弧长增量步为0.1 mm，最大迭代次数为100。

3.3.3 海洋平台桩腿结果分析与讨论

（1）CFRP复合材料密度测试试验

采用DahoMeter直读式电子比重计DH-300测量环氧树脂基碳纤维复合材料的密度。根据ASTM D297-93、D792-00、D618、D891等标准，采用阿基米德水中置换法原理，以实际温度下水的密度为基础，经过两次重量测量分别得出待测样品的质量与体积，CFRP复合材料试样密度测量结果为1 320 kg/m3。

在相同的承载能力、中面直径、桩腿长度条件下，壳体的质量通过壳体中面面积×壳体厚度近似计算。其中，多蛋交接形壳体的中面面积计算公式根据（3）式可得（9）式。

其中，B/L=0.69，L/e=50，n为交接蛋的个数。对于本文研究的三蛋交接形桩腿，B=8 050 mm，n=3，x1=-2 937.6 mm，x2=2 825.4 mm。

经计算可得，三蛋交接形桩腿中间蛋形部分的质量为11.05 t，两端柱形壳部分质量为2.15 t。三种桩腿对应的壳体厚度、材料密度、桩腿质量如表4所示，在相同的轴向承载能力条件下，用复合材料代替一般金属材料可以极大地降低桩腿的质量，降低了海洋平台的施工难度。如将复合材料用于自升式海洋平台的桩腿制造，有力于降低桩腿的插拔桩难度，提高作业效率和海洋平台工作的稳定性。

表4 海洋平台桩腿的质量对比Tab.4 Mass comparison of spud legs of ocean platforms

（2）桩腿线弹性屈曲结果分析与讨论

分别对三种理想海洋平台桩腿进行线弹性屈曲分析，得到前50阶屈曲特征值与失稳模式如表5～7所示。

由表5可知，Q235-A钢柱形壳桩腿的第1阶线弹性屈曲特征值为64 222 kN，第50阶线弹性屈曲特征值为65 626 kN，与第1阶线弹性屈曲特征值相差2.19%。因为存在多组同根值屈曲模态，所以相邻阶屈曲特征值最小偏差为0。相邻阶屈曲特征值最大偏差为0.27%，存在于第12阶与第13阶之间。

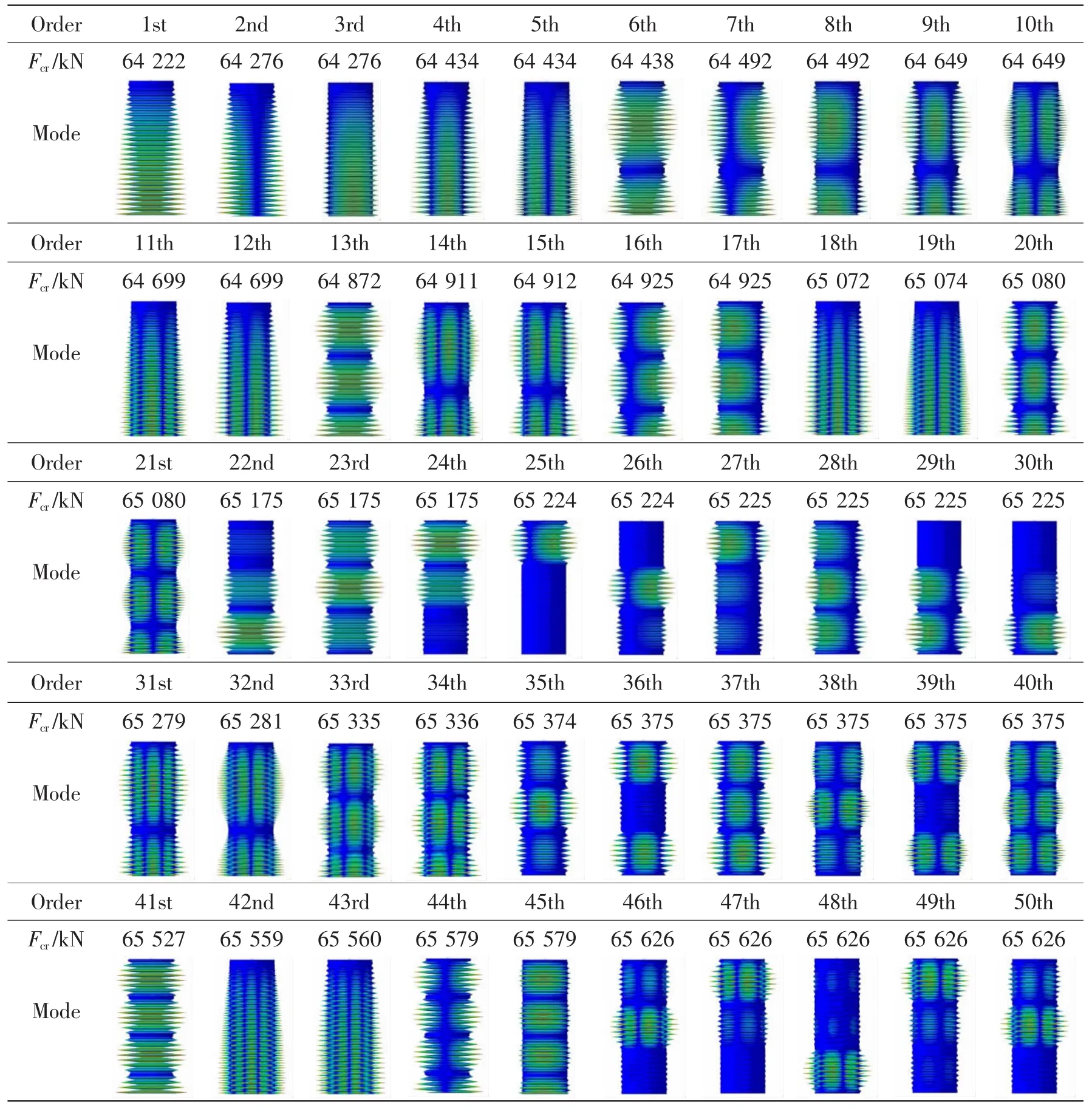
表5 Q235-A钢柱形壳桩腿前50阶轴压屈曲临界载荷与失稳模式Tab.5 50 eigenvalues and buckling shapes of a Q235-A steel cylindrical spud leg under axial compression

由表6可知，CFRP复合材料柱形壳桩腿的第1阶线弹性屈曲特征值为56 502 kN，第50阶线弹性屈曲特征值为61 022 kN，与第1阶线弹性屈曲特征值相差8.00%。因为存在多组同根值屈曲模态，所以相邻阶屈曲特征值最小偏差为0。相邻阶屈曲特征值最大偏差为1.67%，存在于第20阶与第21阶之间。

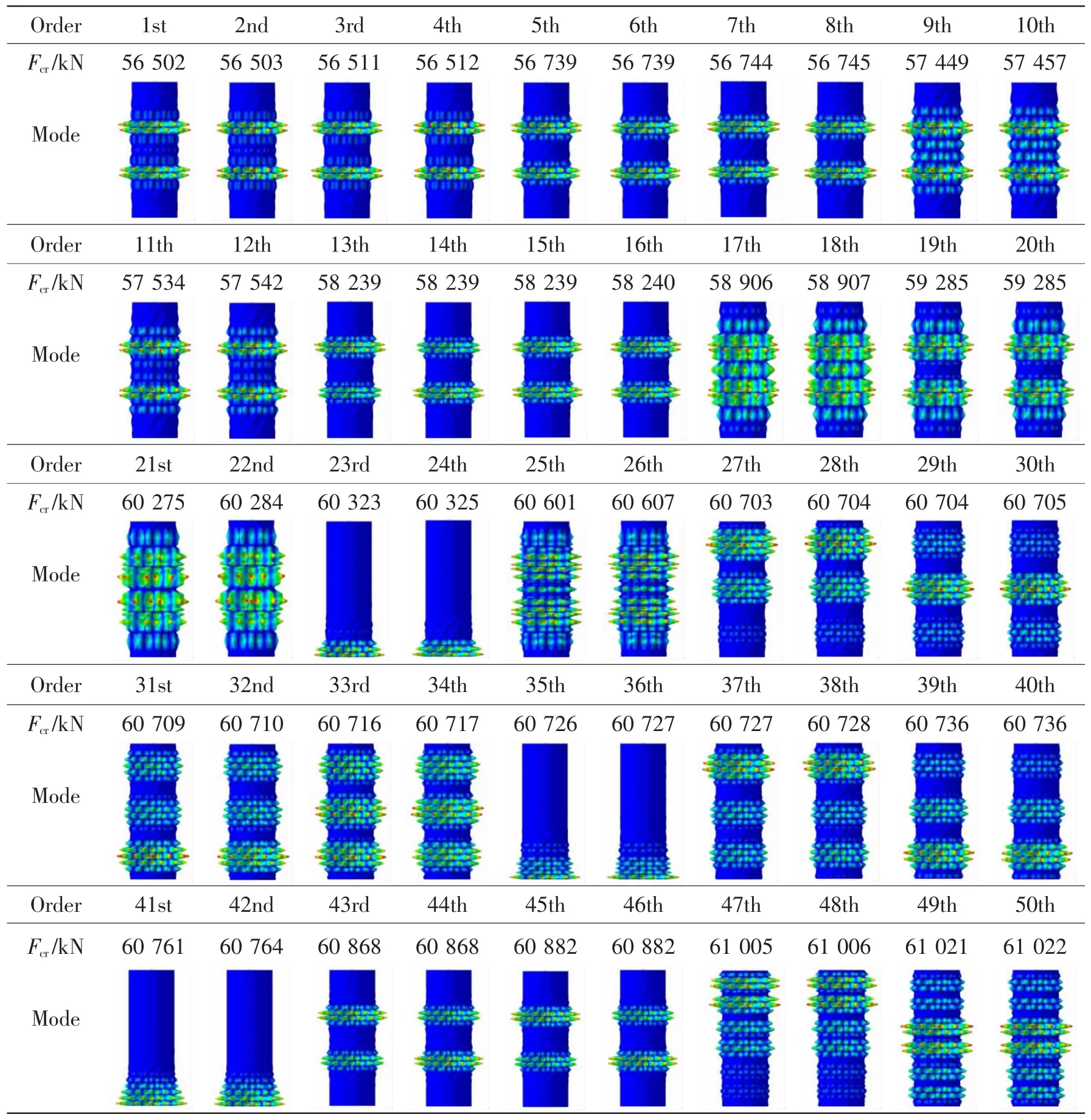
表6 复合材料柱形壳桩腿前50阶轴压屈曲临界载荷与失稳模式Tab.6 50 eigenvalues and buckling shapes of a composite cylindrical spud leg under axial compression

由表7可知，CFRP复合材料多蛋交接形桩腿的第1阶线弹性屈曲特征值为58 647 kN，第50阶线弹性屈曲特征值为63 434 kN，与第1阶线弹性屈曲特征值相差8.16%。因为存在多组同根值屈曲模态，所以相邻阶屈曲特征值最小偏差为0。相邻阶屈曲特征值最大偏差为1.27%，存在于第18阶与第19阶之间。

表7 复合材料多蛋交接形桩腿前50阶轴压屈曲临界载荷与失稳模式Tab.7 50 eigenvalues and buckling shapes of a composite multiple intersecting egg-shaped spud leg under axial compression

续表7

相对于CFRP复合材料桩腿，Q235-A钢制柱形壳桩腿的前50阶线弹性屈曲特征值分散性较小且相邻偏差较小，说明一般金属材料柱形壳桩腿比复合材料柱形壳桩腿具有更高的缺陷敏感度，Q235-A钢柱形壳桩腿是具有相近分立特征值问题的缺陷敏感性结构。因此，通过引入不同缺陷形状与缺陷幅值的模态缺陷研究Q235-A钢柱形壳桩腿和CFRP复合材料柱形壳桩腿和CFRP复合材料多蛋交接形桩腿的缺陷敏感度具有很深远的意义。

（3）桩腿非线性屈曲结果分析与讨论

在5%缺陷幅值的条件下，得到Q235-A钢柱形壳桩腿、CFRP复合材料柱形壳桩腿、CFRP复合材料多蛋交接形桩腿的前50阶模态衰减系数曲线，如图12所示。Q235-A钢柱形壳桩腿的最差阶模态缺陷为第1阶，衰减系数为0.766，衰减系数的极差为0.114；CFRP复合材料柱形壳桩腿的最差阶模态缺陷为第23阶，衰减系数为0.810，衰减系数的极差为0.112；CFRP复合材料多蛋交接形桩腿的最差阶模态缺陷为第9阶，衰减系数为0.913，衰减系数的极差为0.064。CFRP复合材料桩腿的衰减系数曲线均位于Q235-A钢柱形壳桩腿之上，说明缺陷对复合材料桩腿轴向承载能力的影响较小，复合材料柱形壳对缺陷的敏感性较低。复合材料多蛋交接形桩腿相对复合材料柱形壳桩腿具有更好的轴向承载能力，更低的缺陷敏感度。

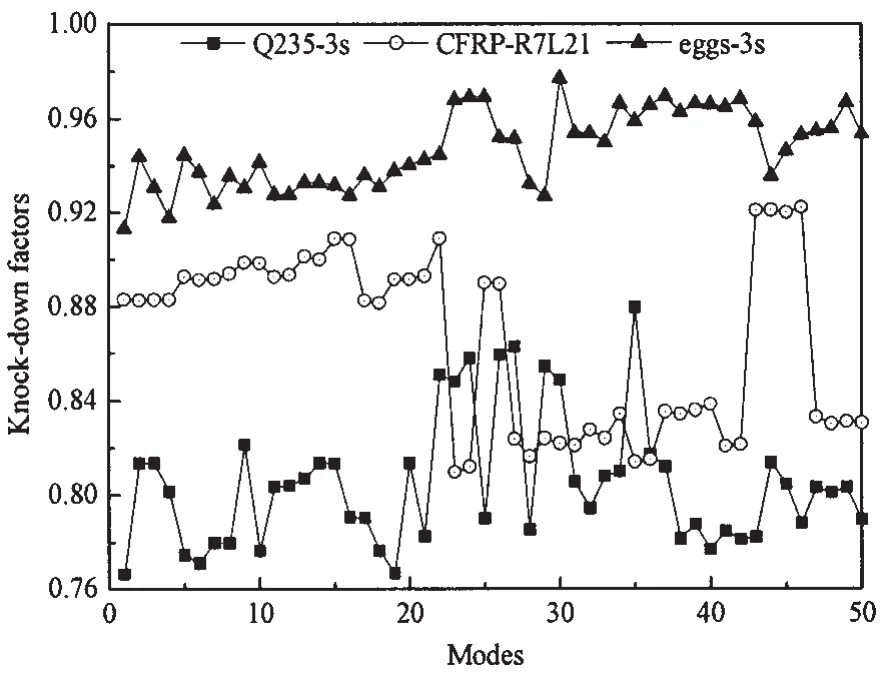
图12 海洋平台桩腿衰减系数曲线Fig.12 Knock-down factor curves of ocean platform spud legs

Q235-A钢柱形壳桩腿5%缺陷幅值的1阶模态缺陷屈曲临界载荷为49 200 kN，相对于线弹性屈曲临界载荷64 200 kN降低了23.36%；复合材料柱形桩腿5%缺陷幅值的23阶模态缺陷屈曲临界载荷为45 800 kN，相对于线弹性屈曲临界载荷56 500 kN降低了18.94%；复合材料多蛋交接形桩腿5%缺陷幅值的1阶模态缺陷屈曲临界载荷为53 600 kN，相对于线弹性屈曲临界载荷58 600 kN降低了8.53%。由此可得，相对一般金属材料，缺陷对于CFRP复合材料桩腿的轴向承载能力影响较小，且CFRP复合材料多蛋交接形桩腿具有更高的轴向承载能力与更低缺陷敏感度。

如图13所示，为5%缺陷幅值的最差阶模态缺陷条件下三种海洋平台桩腿的载荷—位移曲线，图14为最大轴向压缩量下各自对应的非线性屈曲失稳模式。在初始阶段，随着轴向压缩量的增大，轴向压力呈等比例上升趋势，上升速度为Q235-A钢柱形壳桩腿＞CFRP复合材料柱形壳桩腿＞CFRP复合材料多蛋交接形桩腿。当轴向压缩量为25.36 mm时，Q235-A钢柱形壳桩腿载荷位移曲线出现拐点，最先发生失稳，轴向压缩载荷急剧下降，屈曲临界载荷为49 218 kN；当轴向压缩量为63.55 mm时，CFRP复合材料柱形壳桩腿发生失稳，屈曲临界载荷为45 751 kN；当轴向压缩量为123.70 mm时，CFRP复合材料多蛋交接形桩腿发生失稳，屈曲临界载荷为53 554 kN。对于非线性屈曲临界载荷，CFRP复合材料多蛋交接形桩腿比Q235-A钢柱形壳桩腿高出8.81%，比CFRP复合材料柱形壳桩腿高出17.06%。因此，CFRP复合材料多蛋交接形桩腿具有更高的轴向承载能力、更好的稳定性。

图13 海洋平台桩腿5%缺陷幅值的最差阶模态缺陷载荷—位移曲线Fig.13 Load-displacement curves of ocean platform spud legs with 5%imperfection amplitude under worst mode imperfections

图14 三种桩腿最差阶模态缺陷非线性轴压屈曲失稳模式Fig.14 Worst mode imperfection nonlinear buckling shapes of 3-types spud legs under axial compression

4 结 论

（1）缺陷对蛋形壳轴向承载能力的影响远远小于对柱形壳的影响，蛋形壳对缺陷的敏感性较低。等容积蛋形壳相对等质量蛋形壳具有更好的轴向承载能力，更低的缺陷敏感度，对于复合材料柱形壳的形状优化设计具有指导性作用。相对于复合材料柱形壳，复合材料蛋形壳会在更大的压缩量下发生失稳破坏，有利于及时发现设备与结构的隐患与故障，提高了结构的安全性与可靠性。

（2）在相同的轴向承载能力条件下，用复合材料代替一般金属材料可以极大地降低桩腿的质量，降低了海洋平台的施工难度。如将复合材料用于自升式海洋平台的桩腿制造，有利于降低桩腿的插拔桩难度，提高作业效率与海洋平台工作的稳定性。

（3）相对于复合材料桩腿，Q235-A钢制柱形壳桩腿的前50阶线弹性屈曲特征值分散性较小且相邻偏差较小，说明一般金属材料柱形壳桩腿比复合材料柱形壳桩腿具有更高的缺陷敏感度。缺陷对复合材料桩腿轴向承载能力的影响较小，复合材料柱形壳对缺陷的敏感性较低。复合材料多蛋交接形桩腿相对复合材料柱形壳桩腿具有更好的轴向承载能力，更低的缺陷敏感度与更好的稳定性。

[1]Osse T J,Lee T J.Composite pressure hulls for autonomous underwater vehicles[C].Oceans,IEEE-2007:1-14.

[2]European Committee for Standardization.Strength and stability of shell structures:EN 1993-1-6[S].EN Special Publication,2007.

[3]张 建,周 通,王纬波,等.模态缺陷条件下复合材料柱形壳屈曲特性[J].复合材料学报,2017,34(3):588-596.Zhang Jian,Zhou Tong,Wang Weibo,et al.Buckling property of a composite cylindrical shell considering mode imperfections[J].Acta Materiae Compositae Sinica,2017,34(3):588-596.

[4]Jasion P,Magnucki P.Elastic buckling of barrelled shell under external pressure[J].Thin-Walled Structures,2007,45(4):393-399.

[5]Jasion P.Stabilisation of a post-critical behaviour of sandwich cylindrical shells[J].Shell Structures:Theory and Applications,2013,3:195-198.

[6]Blachut J.Strength and bifurcation of barrelled composite cylinders[C].Shell Structures-Theory and Applications:2005,10:203-206.

[7]Blachut J,Wang P.Buckling of barreled shells subjected to external hydrostatic pressure[J].Journal of Pressure Vessel Technology,2001,123(2):232-239.

[8]Blachut J.Combined axial and pressure buckling of shells having optimal positive Gaussian curvature[J].Computers&Structures,1987,26(3):513-519.

[9]张 建,朱俊臣,王明禄,等.蛋形耐压壳设计与分析[J].机械工程学报,2016,52(8):155-161.Zhang J,Zhu J C,Wang M L,et al.Design and analysis of egg-shaped pressure hulls[J].Journal of Mechanical Engineering,2016,52(8):155-161.

[10]张 建,王纬波,高 杰,等.深水耐压壳仿生设计与分析[J].船舶力学,2015,19(11):1360-1367.Zhang J,Wang W B,Gao J,et al.Bionic design and analysis of deepwater pressure hull[J].Journal of Ship Mechanics,2015,19(11):1360-1367.

[11]Zhang J,Wang M L,Wang W B.Investigation on egg-shaped pressure hulls[J].Marine Structures,2017,52:50-66.

[12]Zhang J,Wu J,Wang W B.Investigation on static and dynamic properties of the egg-shaped pressure hull[J].International Workshop on Ship Vibration&Noise IWSVN-2015,2015,10:101-106.

[13]Liang C C,Shiah S W,Jen C Y,et al.Optimum design of multiple intersecting spheres deep-submerged pressure hull[J].Ocean Engineering,2004,31(2):177-199.

[14]Iwicki P,Wójcik M,Tejchman J.Failure of cylindrical steel silos composed of corrugated sheets and columns and repair methods using a sensitivity analysis[J].Engineering Failure Analysis,2011,18(8):2064-2083.

[15]Ross C T F,Little A P F,Chasapides L,et al.Buckling of ring stiffened domes under external hydrostatic pressure[J].O-cean Engineering,2004,31(2):239-252.

[16]Muljowidodo K,Nugroho S A,Prayogo N,et al.Design and analysis of modular composites drybox hull of hybrid autonomous underwater vehicle[J].Indian Journal of Geo-Marine Sciences,2012,41(6):563-568.

[17]Blachut J,Smith P.Buckling of multi-segment underwater pressure hull[J].Ocean Engineering,2008,35(2):247-260.

[18]Blachut J.Experimental perspective on the buckling of pressure vessel components[J].Applied Mechanics Reviews,2013,66(1):010803.