基于边界元法的带空泡航行体的附加质量研究

何振民，王宝寿

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

随着水下航行体的速度增大，航行体表面曲率较大的区域压力急剧降低，不可避免地会发生自然空化现象。带空泡航行体部分或者全部被附着空泡包围，其周围流场的特性和所受的水动力都与全湿流中存在很大不同。在全湿流中，附加质量仅仅与物体的形状和流体密度有关；而当发生空化时，附加质量还与空泡面的变形等存在很大关系[1]。

目前，带空泡物体的附加质量的数值计算方法主要区别于空泡流的模拟，大体可以分为两类：界面追踪方法和两相流模型方法。界面追踪方法假设附着空泡流中存在明显的汽液交界面，通过独立膨胀原理或者边界元法来确定空泡外形（Kinnas和 Fine[2]、Dang和Kuiper[3-4]），与两相流模型方法（黄璇等[5]、弓三伟等[6]、Benaouicha[7]）相比这种方法形式简单，应用方便。陈玮琪和王宝寿[8]基于空泡独立膨胀原理、细长体空泡的经验关系，同时考虑空泡头部外形和空泡尾部的闭合方式，给出了空泡附加质量的理论公式，解释了空泡尾部闭合方式对空泡附加质量的影响。Dang和Kuiper[3-4]在给定空化数的情况下，采用边界元方法迭代得到了无限展长和有限展长水翼的定常空泡形态。Uhlman[1]在给定空泡长度的情况下，同样迭代计算了空化器的轴对称超空泡形态，并借鉴船舶有航速辐射问题的解决方法，在频域中研究了空化器的轴向附加质量。对低频时空化器的轴向附加质量为负值的现象，Uhlman认为与漩涡脱落有关，但是，文中采用边界元法计算非定常流场，实际上并没有考虑漩涡的影响，所以这种解释并不准确。

Uhlman在给定空泡长度的情况下迭代空泡形态和空化数的方法，不便于在工程中迅速得到某一空化数对应的空泡形态。本文结合Dang在给定空化数下迭代水翼空泡形态的方法，将其应用于细长圆柱体，得到了航行体在不同空化数下的定常空泡形态和流场。针对Uhlman只计算轴向附加质量的不足，本文引入速度势的周向变化，对带轴对称局部空泡航行体的轴向、横向和转动附加质量（惯性矩）进行了计算，研究了带空泡附加质量与微幅振动频率的关系，并从存在空泡面变形时流场的特征出发，对这种关系以及轴向附加质量在低频时的负值现象一并给出了一种新的解释。

1 定常空泡和流场的计算

1.1 控制方程和边界条件

为了尽量减小尾空泡的影响，航行体外形采用有半球尾的圆柱体，圆柱段长细比为5，半径取为单位1。定常来流速度V平行于航行体轴线，尾流模型采用回射流模型。图1是过航行体轴线的一个对称面，SB、SC和SJ分别是航行体浸湿面、空泡面和回射流截面。定常流场的速度势Φ0由已知的来流速度势φ0和未知的定常扰动速度势φ两部分组成。由格林公式可知扰动速度势φ满足积分方程：

其中：nq是源点处指向流场外的法向量，rpq是源点和场点之间的距离。

图1 航行体和空泡Fig.1 The vehicle and cavity around it

在航行体湿表面和空泡面上，满足不可穿透条件：

假设定常空泡内的压强等于空化压强pv，空化数为σ，可知空泡面上的流场速度如图1所示的对称面上，沿流线建立弧长坐标系s，则扰动速度势满足

其中：τ是空泡面上弧长的切向量。

对（3）式沿弧长s积分，可以得到空泡面上的速度势

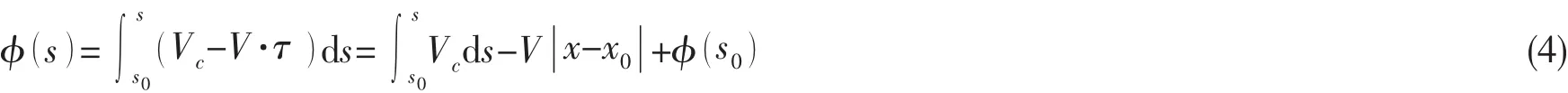
其中：s0是空泡分离点处的弧长坐标，φ（ s0）是分离点处的扰动速度势。

回射流截面SJ是位于空泡面末端的圆环面。在回射流截面上，流体以速度Vc流入空泡内部，由于回射流厚度很小，所以不考虑沿截面的流动，用sJ表示空泡面末端的弧长坐标，可得：

1.2 空泡外形的迭代方案

在给定的空化数下，空泡长度和外形是未知的。空泡分离点固定在航行体头部的几何突变处。本文对空泡初始外形的给定方式进行了研究，发现以Dang采用的厚度沿弧长线性增加的空泡作为初始空泡外形不利于计算的收敛，且不易控制空泡面上的网格疏密。本文结合细长体空泡的特点，由独立膨胀原理[9]给出初始空泡外形，回射流截面会在迭代过程中自行产生和变化。大量的计算表明，这样给定空泡外形能够使迭代步数减少近一半。迭代过程中，湿表面上满足运动学边界条件（2），空泡面上的扰动速度势由（4）式给出，回射流截面上满足（5）、（6）式，得到第一类、第二类混合的Fredholm方程，并通过边界元法离散求解。

由湿表面上的运动学边界条件（2）可知，理想的空泡面应与其上的流场速度相切，根据（7）式修正空泡外形[3-4]，

其中：Δη是空泡面在其法向的修正量，ΔV表示计算所得法向速度与（2）所要求的法向速度之差。迭代过程中需要引入松弛因子，本文中取为0.1。

迭代中，空泡体积是最重要的参数[3]。为了防止偶然因素引起对收敛的误判，本文以连续5次迭代所得的空泡体积都比前一次迭代所得空泡体积改变小于0.1%作为迭代收敛条件。

2 频域中的非定常流场

2.1 方程的建立

将航行体的刚体非定常运动视为在定常运动上叠加了六个自由度的微幅振动，同时可以将非定常流场看作是定常基本流场上叠加了非定常的扰动。流场总的速度势φ可以写成非定常扰动速度势）仍然满足积分方程（1）。由于微幅振动位移、扰动速度势及其空间导数都很小，那么可以得到空泡面和湿表面上的线性运动学边界条件（8）以及空泡面上的线性动力学边界条件[1]（9），

在线性范围内非定常扰动速度势满足叠加原理，那么

考虑（11）式，湿表面上的运动学边界条件可以写成

“m项”包含了定常速度势的二阶空间导数，本文采用文献[10]中的方法计算“m项”。

在回射流截面上，不考虑沿截面切向的流动，有：

用 φj替换（1）式中的 φ，并将（13）式、（14）-（17）式一起代入，得到非定常速度势在湿表面上满足的积分方程（18）和空泡面上满足的积分方程（19）：

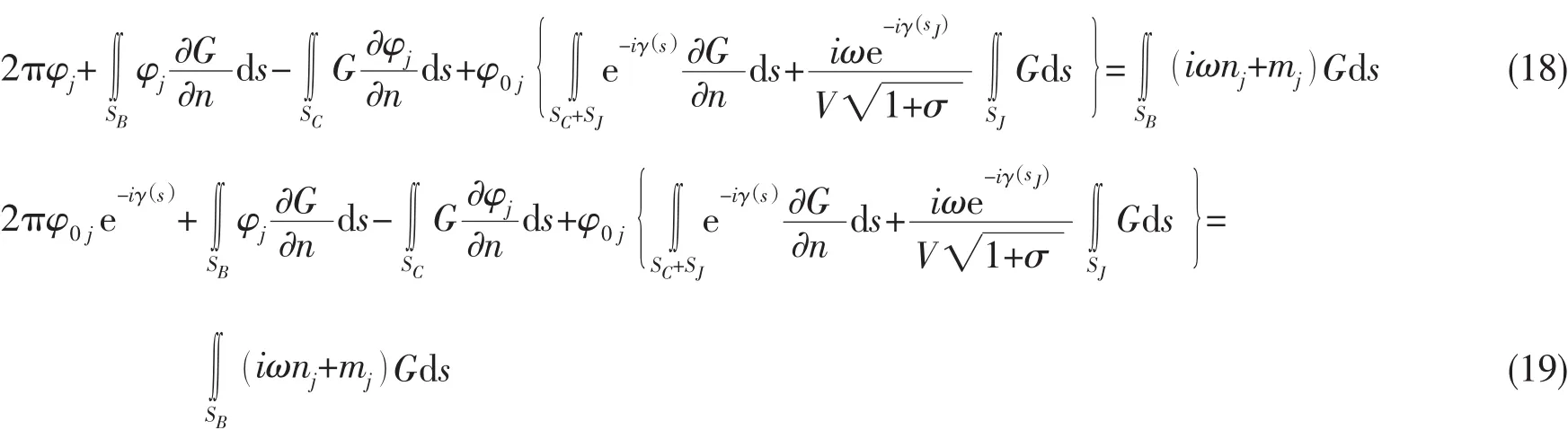
这两式中同时包含了实部和虚部的方程，因而通过边界元法求解时代数方程的阶数会加倍。

2.2 水动力系数

求得非定常速度势后，可得湿表面平衡位置的压强（20）和航行体所受的水动力（21）：

3 结果与分析

3.1 定常空泡形态

图2是本文迭代收敛后不同空化数对应的空泡形态，随着空化数的减小，空泡长度和厚度迅速增长，且空泡形状的变化随着空化数的减小有加速的趋势。

图2 不同空化数对应的空泡外形Fig.2 The shape of cavities on various cavitation numbers

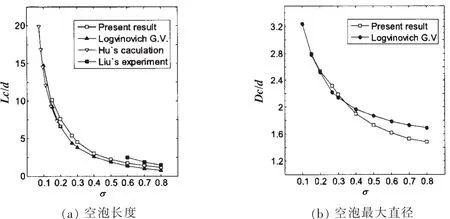
图3 空泡尺度的比较Fig.3 Comparison of the cavity scale

图3是本文迭代所得的空泡无量纲化长度和最大直径与Logvinovich独立膨胀原理、胡晓[11]的Fluent计算结果和刘桦等[12]的试验结果的比较。在空化数较小时，本文所得空泡长度与独立膨胀原理及胡晓的结果都很接近。在空化数较大时，与独立膨胀原理相比，本文所得空泡长度更接近试验结果，同时空泡直径要比独立膨胀原理小，这是因为独立膨胀原理是对小空化数下的圆盘空泡的近似公式，在空化数较大时不准确。可见，本文的结果基于势流理论，采用了回射流模型，满足空泡面和湿表面上的所有边界条件，并考虑航行体尾部影响，所得空泡外形比独立膨胀原理更加接近实际。

图4是空化数等于0.6时航行体湿表面和空泡面上的压强。在航行体尾部附近，压强迅速降低，甚至低于空化压强。这说明此时已经出现了尾空泡，但本文暂不考虑尾空泡的影响。

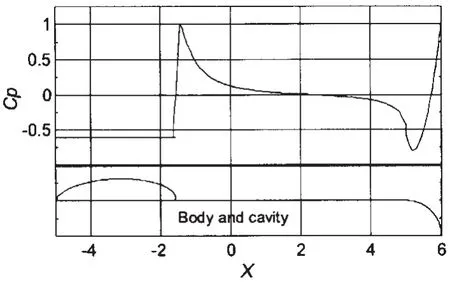
图4 空泡面和湿表面上的压强Fig.4 Pressure on cavity and wetted surface

3.2 带空泡附加质量

为了验证方法和程序的可靠性，首先计算了圆盘空化器在空化数等于0.268时的超空泡轴向附加质量，并与Uhlman[1]的计算结果进行了比较，如图5所示。图中k=wd/V是航行体刚性微幅振动的无量纲频率，附加质量的值被乘以）以方便显示。当频率足够大时带超空泡圆盘的轴向附加质量接近于它在全湿流中的轴向附加质量的一半；随着频率的降低轴向附加质量迅速减小，在足够小的频率下，甚至成为负值。从图5中可以看出本文计算结果与Uhlman的结果是基本一致的。

当航行体作微幅横向振动和转动时，会引起绕航行体和空泡面的横向流动，非定常流场不再是轴对称的。图6是空泡分离圆上的扰动速度势的幅值和相位差β02在周向的分布。由图可看出，横向微幅振动引起的扰动速度势的相位差不随极角θ变化，且在垂直于运动方向的对称面的两侧相差π，而扰动速度势的幅值随θ存在明显的周期性变化。图6说明存在沿周向的流动，并且非定常流场关于前述对称面是反向对称的。上述结论与物理实际完全一致，说明本文的方法可以很好地模拟横向非定常流场。

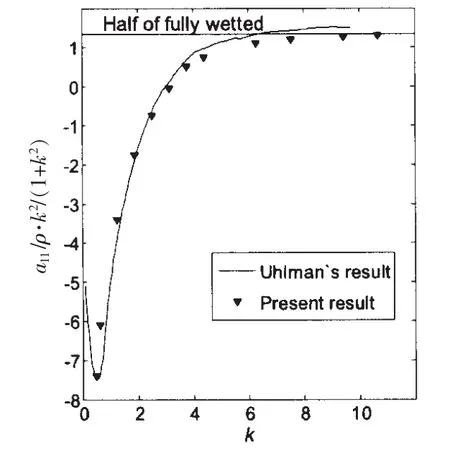
图5 圆盘超空泡附加质量与Uhlman的比较Fig.5 Comparison of added mass of supercavitating disk with Uhlman’s result

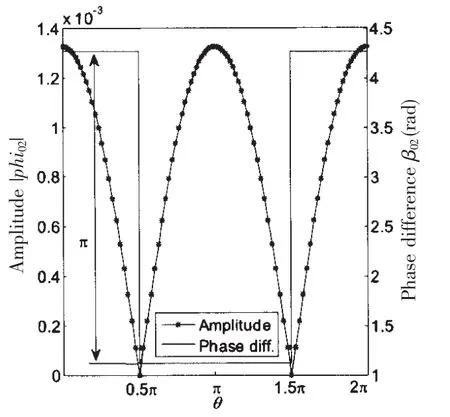
图6 空泡分离圆上的扰动速度势的相位角和幅值沿周向的分布Fig.6 The phase angle and amplitude of unsteady perturbation potential around detachment circle

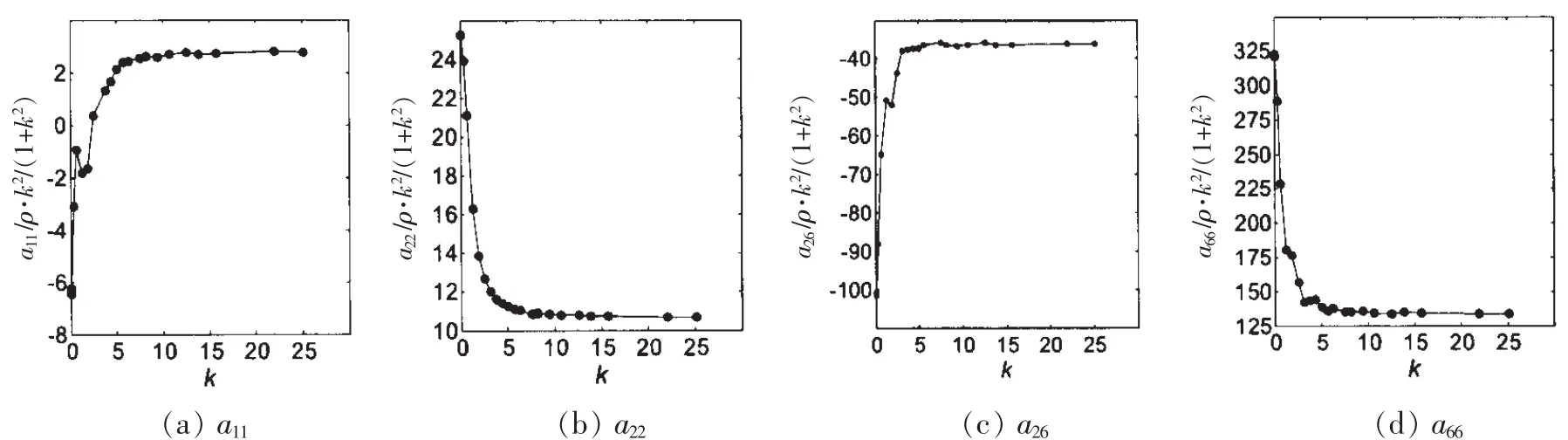
图7 附加质量与无量纲频率的关系Fig.7 Relation between added mass and reduced frequence

当有空泡面存在时，航行体的附加质量与其微幅振动频率有很大关系。图7是空化数等于0.4时航行体的附加质量与频率的关系。当频率足够大时，附加质量的各个分量都分别接近于一个固定的值；而频率减小时，不同分量的的变化有着各自的趋势，a22、a26和a66都增大而a11减小并成为负值，这一点与圆盘超空化时的结果是类似的。

图8反映了空化数和空泡长度对附加质量的影响，图中的附加质量值都是高频下的渐进值，L是圆柱段的长度。从图中可以看出，空化数对a11的影响不大，a11的渐进值约为全湿流中航行体轴向附加质量的82%，而对a22、a26和a66的影响比较显著。随着空化数的变化，a22与相对空泡长度几乎呈线性关系。a26的大小主要取决于航行体湿表面上的压力分布以及质心位置（暂取为圆柱段中点处）。由图8（b）可看出，当空泡长度约为圆柱段长度一半时，湿表面恰好全部位于圆柱段质心后部，a26具有极大值。而a66在空泡长度较短或者较长时变化更快，在空泡长度约为圆柱段一半时变化较慢，这是因为在航行体两端的湿表面积对转动力矩的贡献更大。

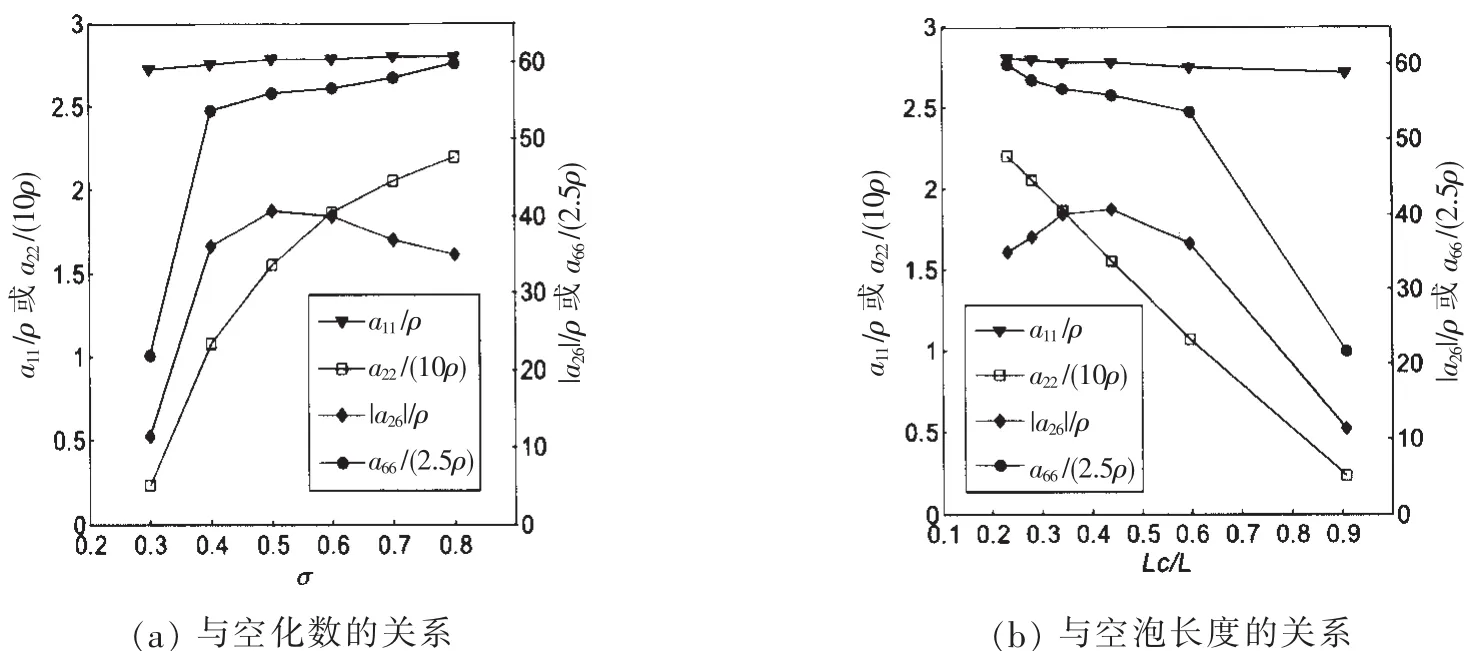
图8 附加质量与空化数、空泡长度的关系Fig.8 Relation of added mass to cavity number and cavity length

图9 分离处扰动速度势的相位角和幅值与频率的关系Fig.9 Phase angle and amplitude of unsteady potential at detachment circle,varies with reduced frequency

前面已经说明，带空泡航行体的附加质量与其非定常运动（刚性微幅振动）频率存在很大关系。当航行体作简谐振动时，空泡面上会激起微幅波，空泡发生变形，空泡周围的流场不断震荡，并进而反作用于航行体。如图9，以空泡分离圆上的一点处的扰动速度势的相位差β0j和幅值与为例来说明流场响应频率的关系。由图可看出，当频率趋近于0时，扰动速度势的相位差先快速变化并最终趋近于π（轴向振动和横向振动）或者0（转动）；当频率增大时，相位差的变化逐渐趋缓。图9说明空泡流场的响应与航行体的运动不是同步的，并且相位差在低频和高频时趋于定值。随着相位差的变化，流场对航行体的作用力的大小和方向相应改变，当流场对航行体的作用力与航行体的加速度反向时，附加质量表现为正值；反之，为负值。扰动速度势的幅值反映了流场响应的强度，对附加质量力的大小也有影响。

带空泡航行体的附加质量与频率的关系，反映了附加质量与航行体的运动历程有关。带空泡水下航行体运动过程中，由于环境的扰动，其速度总是在平均速度附近不规则地波动，附加质量的大小取决于速度波动的频率。

4 结 论

本文通过边界元法计算了水下航行体的定常局部空泡形态及流场，以空化数作为已知量，便于在工程中直接得到不同空化数对应的空泡形态和流场；根据独立膨胀原理给出初始空泡外形，使迭代步数大幅减少。在计算带空泡航行体轴向附加质量的基础上，本文将现有的方法拓展到横向和转动附加质量（惯性矩）。

本文对带空泡附加质量与航行体微幅振动频率的关系进行了研究，高频时，附加质量变化缓慢，并最终趋近于一个定值；低频时，附加质量变化迅速，a22、a26和a66迅速增大，而a11迅速减小并成为负值。针对Uhlman对低频时带空泡轴向附加质量为负值的现象解释的不足，本文从存在空泡面变形时流场的特征出发，对这种现象以及附加质量与频率关系给出了新的解释。

[1]Uhlman,Fine,Kring.Calculation of the added mass and damping forces on supercavitating bodies[C]//4th International Symposium on Cavity.California:California Institute of Technology,2001.

[2]Kinnas S A,Fine N E.A numerical nonlinear analysis of the flow around twoand three dimensional partially cavitating hydrofoils[J].J Fluid Mech.,1993,254(4):151-181.

[3]Dang J,Kujper G.Re-entrant jet modeling of partial cavity flow on two-dimensional hydrofoils[J].Journal of Fluids Engineering,1999,121(4):773-780.

[4]Dang J,Kujper G.Re-entrant jet modeling of partial cavity flow on three-dimensional hydrofoils[J].Journal of Fluids Engineering,1999,121(4):781-787.

[5]黄 璇,鲁传敬,李 杰.带空泡运动航行体的附加质量研究[J].水动力学研究与进展,2009,24(6):800-806.Huang Xuan,Lu Chuanjing,Li Jie.Research on added mass of a cavity running vehicle[J].Chinese Journal of Hydrodynamics,2009,24(6):800-806.

[6]弓三伟,陆宏志,邹正平.弹性体和带空泡体的附加质量动态数值计算[J].计算机仿真,2010,27(4):349-354.Gong Sanwei,Lu Hongzhi,Zou Zhengpin.Hydrodynamic numerical computation of the added mass of elastic body&cavitation bubble[J].Computer Simulation,2010,27(4):349-354.

[7]Mustapha Benaouicha,Jacques-Andre`Astolfi.Analysis of added mass in cavitating flow[J].Journal of Fluids and Structures,2012,31(5):30-48.

[8]陈玮琪,王宝寿.空泡附加质量的理论建模[C].2012年中国造船工程学会优秀学术论文集,2013.Chen Weiqi，Wang Baoshou.Theoretical modeling of added mass of caviting bodies[C].Collection of Excellent Papers for CSNAME in 2012,2013.

[9]Logvinovich G V.Hydrodynamics of flows with free boundaries[M].New York:Halsted Press,1973.

[10]Wu G X.A numerical scheme for calculating the mj terms in wave-current-body interaction problem[J].Applied Ocean Research,1991,13(6):317-319.

[11]胡 晓.水下航行体空泡流数值模拟研究[D].哈尔滨:哈尔滨工业大学,2012.Hu Xiao.Numerical simulation on cavitating flows for underwater vehicle[D].Harbin:Harbin Engineering University,2012.

[12]刘 桦,朱世权,何友声.系列头体的空泡试验研究[J].中国造船,1995(1):1-10.Liu Hua,Zhu Shiquan,He Yousheng.An experimental study on cavitating axisymmetric headforms[J].Shipbuilding of China,1995(1):1-10.