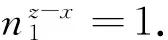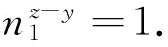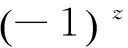关于丢番图方程(48n)x+(55n)y=(73n)z*

李 益 孟

(西南大学， 数学与统计学院， 重庆 400715)

0 引 言

设n是一个正整数，a，b，c是满足a2+b2=c2的正整数.1956年，Jesmanowicz猜想：对任意的正整数n，丢番图方程：

(an)x+(bn)y=(cn)z

(1)

仅有正整数解(x，y，z)=(2，2，2).Sierpinski证明了当n=1，(a，b，c)=(3，4，5)时，方程式(1)仅有正整数(x，y，z)=(2，2，2).Jesmanowicz证明了当n=1，(a，b，c)=(5，12，13)，(7，24，25)，(9，40，41)，(11，60，61)时，方程式(1)仅有正整数解(x，y，z)=(2，2，2).最近管训贵[1]利用对数线性型的下界估计及p-adic赋值，改进了下界，更好地证明了纯指数方程ax+by=(m2+1)z仅有正整数解(2，2，r)，其中r是正偶数，对于其他有关Jesmanowicz猜想的结论请参考文献[2-10].

本研究中，对任意的正整数n，考虑方程式(1)中当(a，b，c)=(48，55，73)的特殊情况，主要利用初等方法得出如下结论：

定理1 对任意的正整数n，丢番图方程

(48n)x+(55n)y=(73n)z

(2)

仅有正整数解(x，y，z)=(2，2，2).

1 引理及定理的证明

引理1 若z≥max{x，y}且a，b，c为正整数，满足a2+b2=c2，则丢番图方程满足(a)x+(b)y=(c)z仅有正整数解(x，y，z)=(2，2，2).

证明已知丢番图方程(48n)x+(55n)y=(73n)z有正整数解(x，y，z)=(2，2，2).假定方程式(2)还有除了x=y=z=2的其他解，由引理1可知，z

情形1x=y

将方程式(2)式化为

nx-z(48x+55x)=73z

(3)

当(n，73)=1时，由式(3)及n≥2，有x-z=0， 即x=z，矛盾.

当(n，73)=73时，令n=73rn1，其中(n1，73)=1且r∈N.于是方程式(3)可变形为

(4)

此时必有n1=1.则

48x+55x=73z-r(x-z)

(5)

显然有z>r(x-z). 对式(5)取模8，有(-1)x≡1(mod 8)，则x≡0(mod 2).设x≡2x1，又因为

所以，z-r(x-z)≡0(mod 2).设z-r(x-z)=2z1，代入方程式(5)中得：55x=732z1-482x1=(73z1-48x1)(73z1+48x1).易知(73z1+48x1，73z1-48x1)=1，则有11x|73z1+48x1或11x|73z1-48x1，然而11x=121x1=(73+48)x1≥73x1+48x1>73z1+48x1>73z1-48x1，矛盾.

情形2x

假设z≤x

nx-z(48x+55yny-x)=73z

(6)

当(n，73)=1时，由式(6)及n≥2，有x-z=0， 即x=z.因此

55yny-x=73x-48x

(7)

对式(7)两边取模11得(-4)x≡4x(mod 11)，则x≡0(mod 2).令x≡2x1，所以有55yny-x=(73x1-48x1)(73x1+48x1).

易知(73x1+48x1，73x1-48x1)=1，则有11y|73x1+48x1或11y|73x1-48x1，而这与11y>11x=121x1=(73+48)x1≥73x1+48x1>73x1-48x1矛盾.

当(n，73)=73时，令n=73rn1，其中(n1，73)=1且r∈N.于是方程式(6)可变形为

(8)

假设x

nz-x(73z-55yny-z)=48x

(9)

当(n，48)=1时，由式(9)及n≥2，有z-x=0， 即x=z，矛盾.

当(n，48)>1时，令n=2r3sn1，其中(n1，6)=1且r，s∈N.于是方程式(9)可变形为

24x-r(z-x)·3x-s(z-x)

(10)

24x-r(z-x)·3x-s(z-x)

(11)

下面将分别讨论r，s的取值情况：

(i) 当r=0，s≥1时，有x=s(z-x)>0，此时必有n1=1.因此，式(11)化为

55y3s(y-z)=73z-16x

因为

所以，z≡0(mod 2).令z=2z1于是55y3s(y-z)=(73z1+4x)(73z1-4x).易知(73z1+4x，73z1-4x)=1，则有11y|73z1+4x或11y|73z1-4x但是11y>11z=121z1>(73+16)z1≥73z1+16z1>73z1+4x>73z1-4x，故矛盾.

(ii) 当r≥1，s=0时，有4x=r(z-x)>0

必有n1=1.因此式(10)化为

55y2r(y-z)=73z-3x

因为

所以，x≡z≡0(mod 2).令x=2x1，z=2z1，于是55y2r(y-z)=(73z1+3x1)(73z1-3x1)，易知(73z1+3x1，73z1-3x1)=2，则有11y|73z1+3x1或11y|73z1-3x1，但是11y>11z=121z1>(73+3)z1≥73z1+3z1>73z1+3x1>73z1-3x1，故矛盾.

(iii) 当r≥1，s≥1时，有4x=r(z-x)，x=s(z-x)，则有r=4s，n1=1.

因此，式(10)化为

55y2r(y-z)3s(y-z)=73z-1

因为

所以z≡0(mod 2).则73z-1≡(-1)z-1≡

情形3x>y

假设z≤y

ny-z(48xnx-y+55y)=73z

(12)

当(n，73)=1时，由式(12)及n≥2，有y-z=0， 即y=z.所以

48xnx-y=73z-55z

(13)

对式(13)两边取模4得(-1)z≡1(mod 4)，则z≡0(mod 2).令z≡2z1，所以有48xnx-y=(73z1-55z1)(73z1+55z1)，易知(73z1+55z1，73z1-55z1)=2，则有24x-1|73z1+55z1，2|73z1-55z1或24x-1|73z1-55z1，2|73z1+55z1.

(i) 若z1≡0(mod 2)，则73z1-55z1≡0(mod 4)，73z1-55z1≡0(mod 3)，所以24x-1·3x|73z1-55z1.但是24x-1·3x>23x·3x=24x>24z>(73+55)z1≥73z1+55z1>73z1-55z1，矛盾.

(ii) 若z1≡1(mod 2)则73z1+55z1≡1+(-1)z1≡0(mod 4).因此2·3x|73z1-55z1，24x-1|73z1+55z1，令n=bc，其中(b，c)=1，且b，c∈N.可得

73z1-55z1=3x·2·bx-y，73z1+55z1=24x-1·cx-y，

因27‖73z1+55z1.则有x=2，与x>y=z矛盾.

当(n，73)=73，令n=73rn1，其中(n1，73)=1且r∈N.于是方程式(12)可变形为

(14)

假设y

nz-y(73z-48xnx-z)=55y

(15)

当(n，55)=1时，则有式(15)及n≥2，有z-y=0， 即z=y矛盾.

当(n，55)>1时，令n=5r11sn1，其中(n1，55)=1且r，s∈N.于是方程式(15)可变形为

5y-r(z-y)·11y-s(z-y)

(16)

(17)

下面将分别讨论r，s的取值情况：

(i) 当r=0，s≥1时，有y=s(z-y)>0此时必有n1=1.因此，式(17)化为

73z-48x11s(x-z)=5y

两边取模3得1≡(-1)y(mod 3)，又因为

(ii) 当r≥1，s=0时，有y=r(z-y)>0.必有n1=1.因此式(17)化为

48x5r(x-z)=73z-11y

两边取模3得：1≡(-1)y(mod 3)，又因为

所以y≡z≡0(mod 2).令y=2y1，z=2z1于是48x5r(x-z)=(73z1+11y1)(73z1-11y1)，而(73z1+11y1，73z1-11y1)=2.所以2|73z1+11y1，24x-1|73z1-11y1或24x-1|73z1+11y1，2|73z1-11y1.但是24x-1>24z-1=28z1-1>27z1>(73+11)z1≥73z1+11z1>73z1+11y1>73z1-11y1，故矛盾.

(iii) 当r≥1，s≥1时，有y=s(z-y)，y=r(z-y)，则有r=s，n1=1.因此式(17)化为

48x5r(x-z)11s(x-z)=73z-1

又因为

综上所述，定理得证。

[1] 管训贵.关于纯指数丢番方程ax+by=(m2+1)z[J].数学进展，2016，45(5)：687-699

GUAN X G.On the Pure Exponential Diophantine Equationax+by=(m2+1)z[J].Advances in Mathematics，2016，45(5)：687-699

[2] LE H.A Conjecture Concerning the Pure Exponential Diophantine Equationax+by=cz[J].Acta Math Aug，2005，21(4):943-948

[3] MIYAZAKI T. On the Conjectureof Jesmanowicz Concerning Pythagorean Triples[J]. Bull Austral Math Soc， 2009， 80: 413-422

[4] YANG Z J，TANG M.On the Diophantine Equation (8n)x+(15n)y=(17n)z[J].Bull Austral Math Soc，2012，86(2):348-352

[5] SUN C F，CHENG Z.A Conjecture of Jesmanowicz Concerning Pythagorean Triples[J].Adyances in Mathematics，2014，43(2):267-275.

[6] 苟莎莎， 张洪. 关于丢番图方程(16n)x+(63n)y=(65n)z[J]. 西南师范大学学报(自然科学版)，2015，40(4):4-7

GOU SS，ZHANG H.On the Diophantine Equation (16n)x+(63n)y=(65n)z[J].Journal of Southwest：Normal University:(Natural Science Edition)，2015，40(4):4-7

[7] 邓谋杰. 关于丢番图方程(15n)x+(112n)y=(113n)z[J]. 黑龙江大学(自然科学学报)， 2007， 24(5)： 617-629

DENG M J.On the Diophantine Equation (15n)x+(112n)y=(113n)z[J].Journal of Heilongjiang University (Natural Science)，2007，24(5):617-629

[8] 薛阳， 高丽. 关于丢番图方程(20n)x+(99n)y=(101n)z[J]. 延安大学学报(自然科学版)， 2016， 35(3):16-19

XUE Y， GAO L.On the Diophantine Equation (20n)x+(99n)y=(101n)z[J].Journal of Yanan University(Natural Science Edition)，2016，35(3):16-19

[9] 王聪.关于不定方程x(x+1)(x+2)(x+3)=30y(y+1)(y+2)(y+3)[J].重庆工商大学(自然科学版)，2016，33(1)：29-32

WANG C.On the Diophantine Equation (20n)x+(99n)y=(101n)z[J].Journal of Chongqing Technology and Business University(Natural Science Edition)，2016，33(1)：29-32

[10] 唐刚. 关于丢番图方程(45n)x+(28n)y=(53n)z[J]. 西南民族大学学报(自然科学版)， 2014，40(1):101-104

TANG G.On the Diophantine Equation (45n)x+(28n)y=(53n)z[J].Journal of Southwest University for Nationalities (Natural Science Edition)，2014，40(1):101-104