基于量纲分析法的单摆周期进一步推演
杨汝娟,方 雪
(1.丽江市第一高级中学,云南 丽江;2.云南师范大学物理与电子信息学院,云南 昆明)
量纲分析是日常物理教学中重要的板块之一,其基本原理主要是量纲和谐原理和Ⅱ定理,其中量纲和谐原理适用于比较简单的物理问题,如果相关变量的未知数不超过5个,而Ⅱ定理则具有普遍使用性。本文通过量纲分析单摆中的周期,说明在物理实验中解决问题的便利性。
在物理学中导出物理量在SI单位制下由七个基本量构成:长度L,质量M,时间T,电流强度I,温度K,光照强度Θ和物质的量N,一个所研究物理量的量纲可以用以上的七个基本量的幂次方的乘积 f=LαMβTχIδKεΘφNγ表示,称这个幂次方乘积的数学关系为该物理量的量纲解析式,其中 α、β、χ、δ、ε、φ、γ 为常数,称为量纲指数。若一个研究的物理量的量纲指数全部为0,则称该物理量为无量纲量。
一、量纲和谐原理
量纲和谐原理是指凡能正确反映客观规律的物理方程,其各项的量纲都必须是一致的。因为只有相同量纲的量才能相加减,否则是没有意义的。所以一个方程中各项的量纲必须是一致的,例如连续方程、能量方程和动量方程各项的量纲都是一致的,也就是说各方程式的量纲是和谐的,而且方程的形式不随单位制的变化而改变。
二、π定理与量纲齐次法则
在研究一个物理现象中,所涉及完整的关系式都可以是无量纲化的。假设某一个物理现象中相关参量有X1,X2…Xk…Xn,之间存在着如下的关系:φ(X1,X2…Xk…Xn)=0
式中 X1,X2…Xk…Xn是由 Z1,Z2…Zk…Zn中 k 个独立量纲的参量所组成的无量纲参数,通过对原来n个参量的无量纲化,一定可得到n-k个独立无量纲参数X1,X2…Xk…Xn-k的函数关系式,这就是所谓的π定理。
由上述的函数关系,设有m个基本量物理量,则可组合形成m*n阶矩阵,假使该矩阵的秩为r,则有n-r个基本解:Y1,Y2…Y(n-r),使得φ(Y1,Y2…Y(n-r))=0与φ(X1,X2…Xk…Xn)=0相互等价,称为量纲齐次法则。

图1 单摆示意图
三、理想情况下单摆做小角度振荡的周期量纲分析
单摆是在细绳的一端悬挂着一个具有一定质量的物体,细绳的另一端是固定不动的,而且细绳的质量m比悬挂的物体的质量要小得多,可忽略不计,细绳的形变比绳长l小得多也可以忽略不计,当悬挂物从铅垂的自热状态,沿半径为l的圆弧移动到初始方位角,然后无初速度释放,物体受重力的作用下作周期性振动,如图1所示。
显然,单摆的振荡周期t取决于与该物理现象相关的4个参数,即悬挂物的质量m,细绳的长度l,当地重力加速度g以及运动的初始方位角α,于是我们可以得到单摆的振荡周期t与悬挂物的质量m,细绳的长度l,当地重力加速度g以及运动的初始方位角a之间的关系:

显然,这里描述的是一个简单的力学系统,在函数t=f(m,l,g,α)中的自变量,有三个量纲是独立的基本量,即m、l、g它们的量纲分别是质量(M)长度(L)和重力加速度(g)。上述函数关系式中的α为运动的初始方位角;而因变量t的量纲是时间(T),可以表示为基本量l、g之间的量纲组合,而振荡周期t与初始方位角α都是导出量,于是我们进行如下量纲矩阵分析:
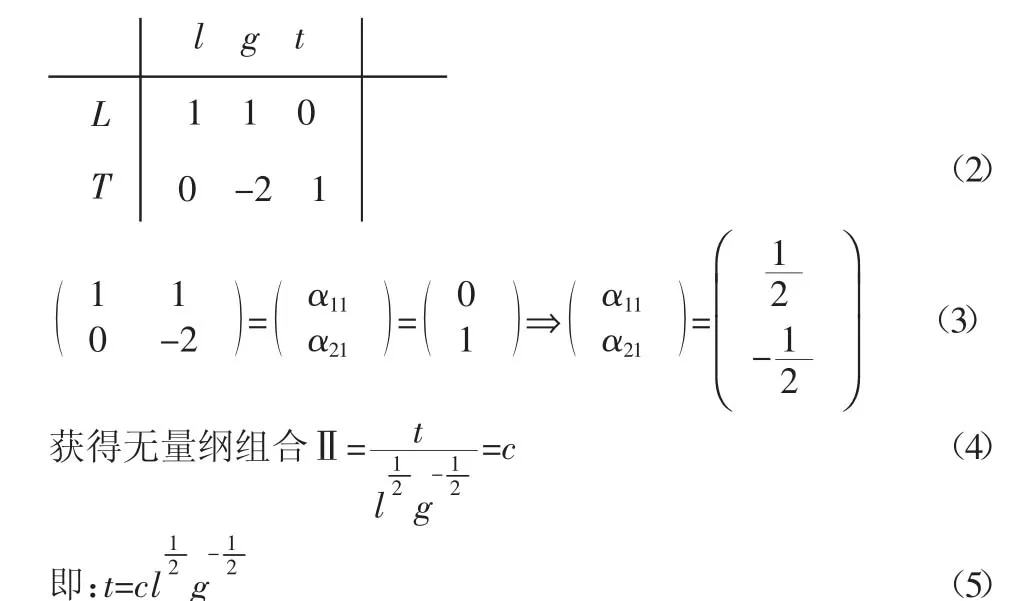
我们可以把m、l和g取为该问题的基本单位系统,用来度量问题中所有的物理量,根据(1)(2)(5)式可得:


图2 单摆示意图
如图2所示,设单摆的摆锤处于最低点时势能为零,摆角为θ时摆锤上升的高度y为:

此时单摆的总的机械能为:


不计空气阻力影响,则单摆的机械能守恒,由(9)(10)式得:


则式(12)变为:

由式(13)可得:

由于k<1,sinu<1,式(14)被积的函数中二次方以上项的值近似为零,可忽略不计,于是有

f(α)实际上是α的偶函数,如果初始方位角α是个很小的角,将f(α)在α=0处作泰勒展开,于是有:

将(17)式带入(7)式有:

可见,我们使用量纲分析的方法来寻找t=f(m,l,g,α)的关系只需做6组以上的实验来确定f(α)就足够了,而使用传统的测量的方法寻找的t=f(m,l,g,α)关系,假设对于每一个自变量测量10次,那么共要做10*10*10*10次实验,相比来看,益处太明显了。
四、小角度下空气阻尼系数对单摆周期的影响
单摆在空气的运动是存在阻尼的,而且阻尼系数非常小,但是对摆的运动存在巨大的影响,我们对摆在空气中的运动进行分析可以知道,摆的运动周期在大角度下是非线性的,而在小角度下的运动是线性的,摆在空气中的运动周期t可能和质量m、当地重力加速度g、阻尼系数k、摆长l、速度v有关,这里选择m、g、k、l、v为基本量进行如下分析:

获得无量纲组合:

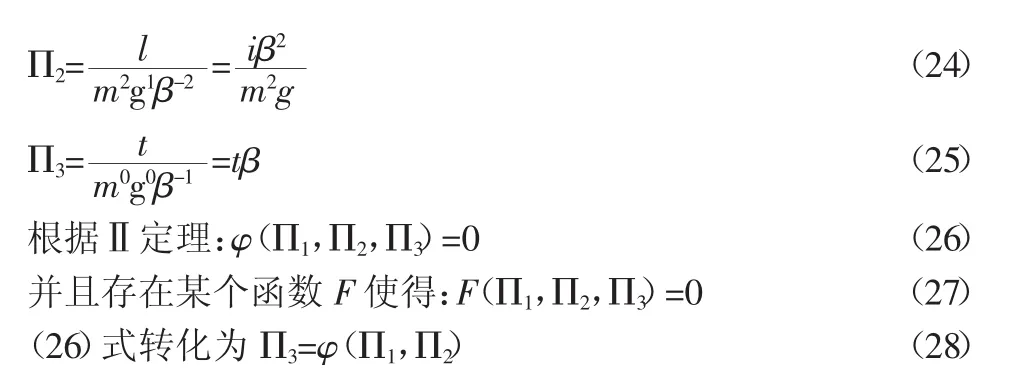
式中是某个函数,由(23)(24)(25)式得:

同时乘以质量m

下面我们采用正交实验方法的思想确定函数φ的具体形式;
函数关系式,可以用以下函数关系式表示:
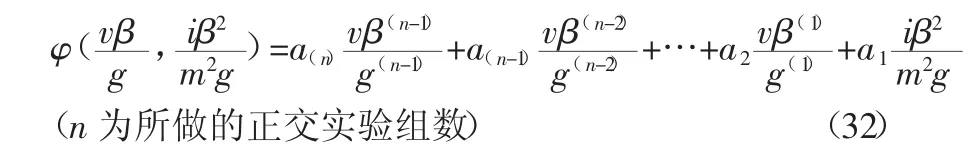
由函数方程式(29)式可得:

(33)式转化为

现在对(34)式分析:
将(34)式转化为
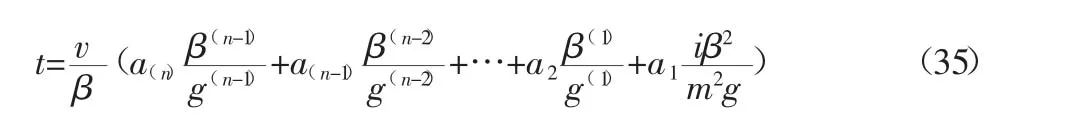
将(30)式带入(35)式得

(说明:α为摆的初始方位角,θ为摆在运动的过程中移动的方位角,n为所做的正交实验组数。)
结合单摆的分析,利用量纲分析法阐述了单摆周期的物理分析,可以得出量纲分析对于某一物理现象可以有效地进行物理方程的确立,但由于量纲分析的结果是半定量化的,其中有一些无量纲的参数或函数难以确定,这些参数或函数还需进一步使用其他工具计算,但是量纲分析出的变量之间的关系,可以减少所研究的物理问题的不确定因数。在此基础上,对于所研究问题的数学模型的建立与确定关系式的一般函数形式,具有较大的实际意义。
——以匀加速直线运动公式为例

