从一道三角试题谈数学核心学习力的培养

金雅芳

（浙江省绍兴市上虞区浙江省春晖中学，浙江 绍兴）

【例题】在△ABC中，acosB=bcosA，且边BC上的中线长为4．求△ABC面积的最大值．

【分析】从面上看，本题非常符合解三角形的考试要求：掌握正弦定理、余弦定理及其应用，并能对面积公式进行适当应用；也非常符合解三角形的本质：考查方向从边到角或是从角到边，在边角互化的过程中体会函数思想、化归思想．其实先利用正弦定理，马上可得：

sinAcosB=sinBcosA⇨sin（A-B）=0，即 A=B．

一、函数的“等效”

☆流程图：设变量→建立函数关系式→求一元单变量函数的最值问题．

【解法1】取线段BC的中点为M，设AC=BC=2x，则CM=x可得

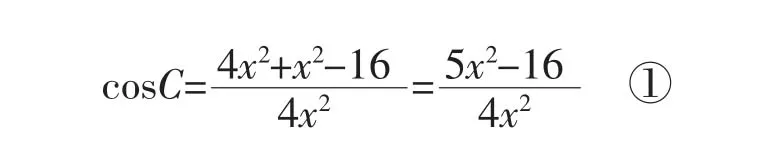
由①可得：

则

则

研究②式，也可利用asinx+bcosx的最值建立不等式关系：

可化简为5S-4ScosC=32sinC

移项得：4ScosC+32sinC=5S ③

二、图形的“等效”

☆流程图：看图形特征→建立直角坐标系→联系一元单变量函数的结构特征→求最值．

在代数式的转化过程中，很多时候均可以采用几何元素来进行考查．

如研究上面②式也可采用：

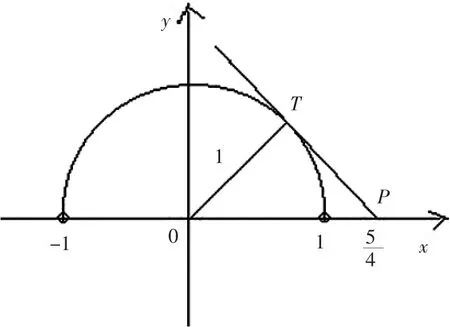
【解法2】题中已知三角形为等腰三角形，也可考虑建系完成．

以线段AB所在直线为x轴，中垂线为y轴建立直角坐标系，设 A（-a，0），B（a，0），C（0，b），又设边 BC 的中点为

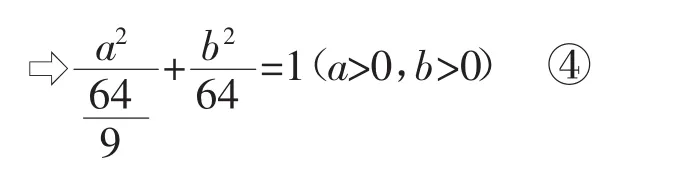
现行新课标数学教材（普通高中数学课程标准，人民教育出版社，A版）主编寄语中指出：数学是自然的，是水到渠成、浑然天成的，不仅合情合理，甚至很有人情味，学习数学要摸索学习的方法，数学学习要摸清数学学科素养，积极培育学生的学科思维能力．数学又是自由的，是包罗万象的基础，对抽象、一般的事物，要积极发挥想象的空间．因而，在数学教学中，也要使数学概念的呈现、思维的形成发展、方法的生成应用、学习能力的提升成为自然、必然而水到渠成的，使学生体会到数学的自然、有用、有趣、严谨而生动，从而充满兴趣地积极参与到数学教学活动中，主动思考探究数学知识、方法，形成数学思想，提升数学学习能力．明年全国推进新一轮的课程改革，浙江省又是改革先锋，作为数学老师，期待着数学“芯片”的产生!