高维数据离群点检测的局部线性嵌入方法

邓廷权，刘金艳，王宁

哈尔滨工程大学理学院，哈尔滨150001

高维数据离群点检测的局部线性嵌入方法

邓廷权，刘金艳，王宁

哈尔滨工程大学理学院，哈尔滨150001

CNKI网络出版：2017-03-04,http://kns.cnki.net/kcms/detail/11.2127.TP.20170304.1727.006.html

1 引言

离群点或者异常值通常具有异乎寻常的信息。离群点[1]有时又被称为异常点、野值点、例外点、噪声点、偏离点、新颖点、异常物等，在这里统一称作离群点。离群点是指可能由某种机制产生的偏离大多数样本的点，信用卡欺诈检测、网络入侵检测、自然灾害预测和运动员的异常能力检测等等通常能带来许多重要的信息。因此离群点检测引起了人们越来越多的关注。离群点产生的原因主要有三种：（1）实验产生的误差，可能是数据测量与收集产生的误差，也可以称为噪声点，理论上应该去除。因为它们不仅不能提供有用的信息，还有可能降低数据的质量。（2）数据来自于不同的类，这种离群点是研究的重点，如信用卡欺诈就是盗窃信用卡的人与信用卡拥有者可能具有不同的用卡习惯，因此他们属于不同的两类，这种情况下的信息是非常重要的。（3）自然变异，这种情况可能是自然产生的，未必是变异的异常。

离群点检测的经典方法主要有基于距离的离群点检测方法[2-3]，找出每个点的k-最近邻距离，将求出的距离按降序进行排列，应用topn方法把距离大的点作为离群点。江峰[3]提出了一种新颖的基于距离与边界的离群点检测方法（BD）。基于k最近邻（KNN）的离群点检测方法是经典的基于距离的方法，虽然基于KNN[4]聚类的离群点检测方法容易实现，但是该算法值得进一步的研究。首先基于KNN的离群点检测方法对参数k敏感，当近邻点数k有一个小的变化时，可能引起离群因子和相应的离群点的变化，因此文献[4]提出了基于最小生成树的KNN启发式方法来发现离群点，克服参数k的影响。其次，对于含有多个属性的高维数据而言，寻找每个点的k-最近邻是非常耗时的。最后，在高维空间，可能存在着维数灾难问题，数据点之间的距离可能都是相等的。从而，在高维空间中，人们开始质疑基于距离的离群点检测方法的合理性。还有基于密度的离群点检测方法，如局部离群因子（LOF）方法[5-7]、基于统计的方法、基于深度的方法以及基于聚类的方法[8-10]。文献[8]中提出了一种基于模糊粗糙C均值的半监督离群点检测方法（FRSSOD），通过利用标记样本并结合模糊粗糙C均值聚类方法，达到较好的检测离群点的效果。

随着数据量的增大，数据的维数也在不断增长，人们需要面对可能由此带来的维数灾难问题。对于高维数据集来说，许多传统的离群点检测方法并不能有效地检测出离群点[11-13]，因为高维空间数据点分布比较稀疏，根据距离判断k近邻[14-15]、密度以及聚类都是不合理的。为了解决这个问题，一些方法尝试将高维数据投影到低维子空间，在低维空间中通过距离、密度、聚类方法来检测离群点。这些方法一般是将维度进行组合，对每一个可能的子空间进行投影，选出效果最好的子空间。但是随着维数的增加，导致存在组合的子空间数量非常多，计算量非常大。Aggarwal提出了高维数据离群点检测需要满足以下条件：能够有效地解决高维数据的稀疏问题；能够对数据的异常进行解释；能够给出子空间的物理意义；计算高效性及要考虑数据点的局部结构。

众所周知，局部线性嵌入（LLE）[16-18]是一种非线性的维数约减方法，它将高维数据集降至低维空间的同时保持样本间的局部线性结构，但它容易受到噪声的影响。拉普拉斯映射（LE）[19-20]也是一种非线性的维数约减方法，它将高维数据降至低维空间的同时保持数据间的局部近邻结构，同时它对噪声不敏感。基于这两种方法的特点，本文应用流形学习的方法对高维数据进行降维，可以有效地避免组合的子空间数量非常多，计算量非常大的问题。由于离群点一般都在数据集的边界上，本文通过建立一种有效的粗糙集模型，将数据集的下近似中的点保持局部线性结构，将所有样本点保持局部近邻结构，确保在降维的过程中使离群点远离正常点，进而在低维空间中使用基于最小生成树的KNN启发式方法，能够更简单有效地检测出异常值。本文提出的方法不仅能够达到对高维数据集进行离群点检测所需的5点要求，而且一系列实验证明了它检测离群点的有效性。

2 经典LLE和LE降维方法

2.1 局部线性嵌入

Roweis和Saul在2000年提出了一种解决非线性维数约减的方法叫做局部线性嵌入（LLE）。由于该方法简单，参数较少，容易实施，适用于非线性数据集以及最优解不容易陷入局部最小等优点，因此被广泛应用。LLE通过保持数据的局部线性结构来恢复潜在流形。

得到。对于每一个点xi：

如果Gi=(Gjl)可逆，则可以得到：

其中第一个限制移除了旋转平移自由度，第二个限制要求输出变量在一定的范围内。式（2）的等价表示如下：

其中M=(I-W)T(I-W)，所以求解优化问题（3），转化为求M最小的d+1特征值所对应的特征向量。由于最小的特征值为0，所以被舍掉。

2.2 拉普拉斯映射

拉普拉斯映射（LE）是由Belkin和Niyogi在2003年提出的一种经典的非线性维数约减方法。LE方法将高维数据集映射到低维空间的同时保持数据点间的局部近邻结构，且对噪声不敏感。

整理优化问题（4）并利用拉格朗日乘子法，优化问题（4）可以转化为求如下广义特征值问题：

公式（5）的最小的d个正的特征值所对应的特征向量就是高维数据映射低维空间的映射结果。

3 局部线性嵌入的离群点检测方法（OLLE）

由于高维数据集中不同属性的范围差异非常大，数值大的属性计算距离时占很大的比重，导致可能忽略其他属性的重要信息，因此需要对数据进行预处理。

利用如下方法对数据集进行归一化处理：

为每一个点xi(i=1,2,…,n)寻找近邻集时，首先计算样本xi与数据集X中所有样本的距离，找到第k个最小距离dik，根据阈值dik，构造样本xi的近邻集N(xi)：

根据每个样本xi得到的近邻集，可以计算出样本点与所有近邻点之间的平均值di：

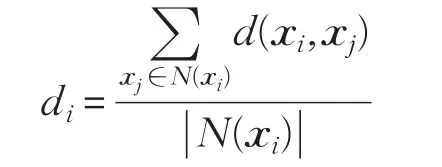
为每个样本xi的每一个近邻点xj∈N(xi)，计算出与N(xi)中样本之间的平均值dj，根据得到的||N(xi)个值，再计算出个值的平均值：

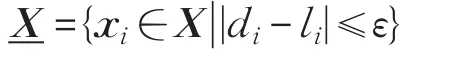
显然，对于每一个点xi来说，如果满足就说明xi点在下近似集合中，否则在边界集合中。可以看出在下近似集合中的点与周围点距离偏差不大，因此稀疏情况比较一致。然而在边界中的点与周围点距离偏差比较大，因此这些点是离群点的可能性就会相对大一些。

对下近似中的每一个样本点xi，定义点xi的近邻集

由于LLE对噪声敏感，对所有样本点保持局部线性结构是不合理的，因为边界的点可能是离群点，影响降维的效果。所以在这里对下近似中的点保持局部线性嵌入。

考虑每个样本点xi(i=1,2,…,n)与它的近邻集(xi)，构造如下重构误差：

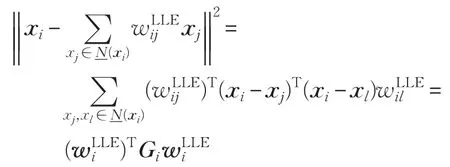
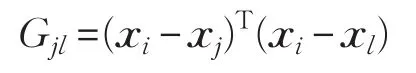
构造如下优化问题：

由此可以求解出重构的权矩阵：

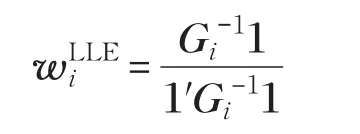
为了避免噪声的影响，将高维数据集降至低维空间时，又希望可以保持数据样本之间的局部近邻结构。因此，对整个数据集构造一个加权近邻图，利用热核法为近邻点之间赋权值：如果xi∈Nk(xj)或xj∈Nk(xi)

显然，如果样本点xi和xj是近邻关系，且xi和xj之间距离越小，则权值w′ij越大。如果样本点xi和xj不是近邻关系，则权值w′ij为0。

目的是将高维数据降至低维空间后，可以有效地检测出离群点，所以希望离群点在低维空间中离正常点越来越远。故构造出如下一个权重w″ij：

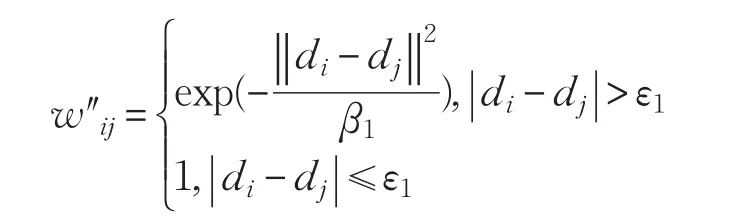
其中ε1是一个给定的阈值，di表示样本点xi与近邻集N(xi)中所有样本的距离平均值，dj表示样本点xj与近邻集N(xj)中所有样本的距离平均值。如果di和dj偏差不大，说明xi与xj的稀疏情况比较一致，样本xi与xj是离群点的可能性很小，因此赋予一个大的权值。相反，当di和dj偏差大于一定的阈值时，表明样本xi与xj中可能有一个点为离群点，根据距离赋权值，因此权值w″ij较小。

由于将高维数据降至低维空间中，不仅试图保持下近似集中的样本之间的局部线性结构，而且也希望保持全部数据样本之间的局部近邻结构，同时确保离群点远离正常点。因此构造如下优化问题：

其中ρ是一个实参数，权衡第一项保下近似集中样本之间局部线性结构与第二项保全部样本的局部近邻结构同时拉开离群点与正常点之间的距离对优化问题的影响。在这里D‴是一个对角阵，由于：

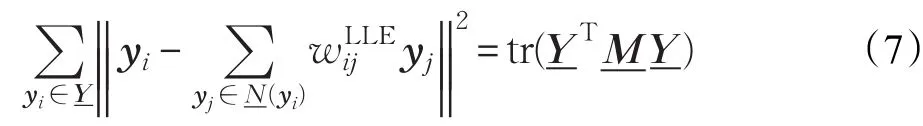
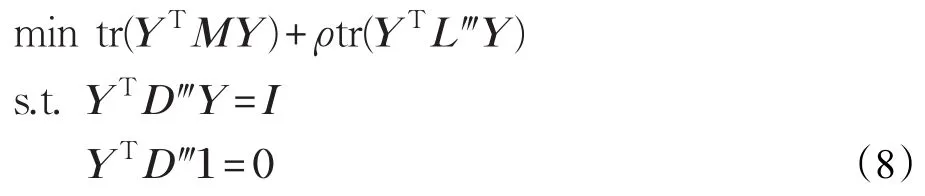
令H=M+ρL‴，则H也是一个n×n矩阵，从而式（8）可转化为：根据拉格朗日乘子法，将上述优化问题转化为解如下广义特征值问题：

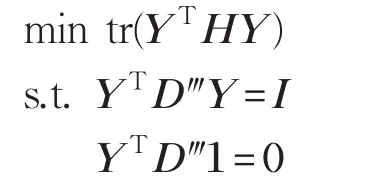
公式（9）的最小的d+1个特征值所对应的特征向量就是高维数据映射到低维空间的映射结果。因为最小的特征值是0，或者接近0，然而任何向量都可以作为0的特征向量，所以舍弃了第一个特征值来保证输出变量的唯一性。

由于基于KNN聚类的离群点检测方法容易实现，但受参数k的选择影响很大。本文采用基于最小生成树的KNN启发式方法[4]（MST-KNN）来检测离群点。

4 实验与分析

所有的实验都是在Windows 7机器上运行的，电脑具有以下配置Intel®Pentium®双核，2 GB内存，并且所有方法都是在MATLAB R2009a上实现的。

采用8个数据集对本文提出的算法进行分析实验。Iris、Cancer、Wine、Zoo和Wdbc等五个数据集取自于UCI数据库。Iris数据集有三类，前两类全部选取，在第三类中只选取4个点，并将这4个点看作离群点；Cancer数据集总共有两类，从第一类中选取210个点，第二类选出2个点并看作离群点；在Wine数据集中，选取64个点做测试，其中59个点取自一类，5个点取自另一类，并将这5个点看作离群点；在Zoo数据集中，选取45个点，其中41个点取自一类，4个点取自另一类，将这4个点看作离群点；数据集Wdbc中358个点来自一个类，20个点来自另一类，把这20个点看成离群点；Optical handwritten和Mnist都是数字数据集。在Optical handwritten中选取409个点做测试，其中390个点来自一类，其他20个点来自另一类，并把这20个点看做离群点。数据集Mnist中前800个点都是数字1，后10个点来自数字2，并把这10个点看做离群点。PIE为人脸数据集，在PIE中选取216个点做测试，其中包括5个人的人脸图像，前四个人每个人49张图像，最后一个人的20张图片被看做异常点。数据特征如表1所示。

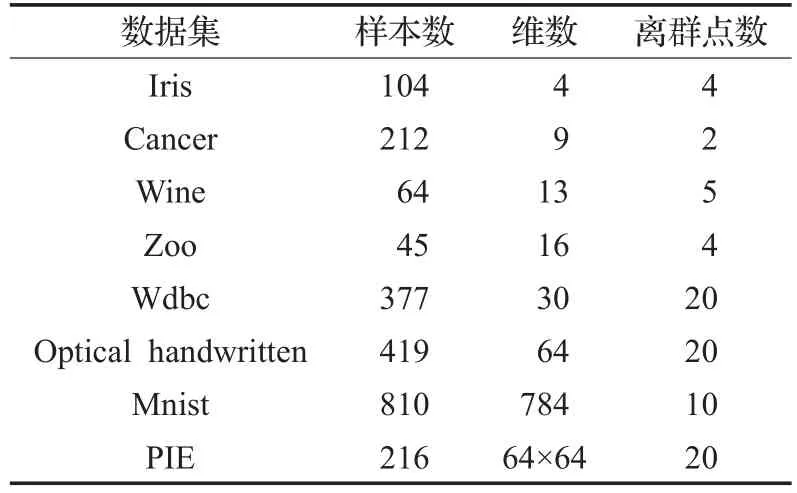
表1 数据集描述

4.1 OLLE可视化图形

由于高维数据点分布稀疏，使得高维空间中数据之间的距离尺度与区域密度不再具有直观的意义。因此，在将数据集从高维降至低维空间的同时保持局部几何结构，且让离群点与大多数点远离，进而在低维中来检测离群点。

对UCI中的Wine、Cancer和Iris三个数据集进行二维可视化表示。Wine数据集中选取64个样本点，其中包含5个离群点；Cancer数据集中选取212个样本点，其中包含2个离群点。Iris数据集中选取104个样本点，其中包含4个离群点。在这两个实验中设置参数ε=0.2，ε1=0.003,ρ=1，第三个实验参数是ε=0.4，ε1=0.003，ρ=1，k分别为10、8、10。图1～3分别为数据集Wine、Iris和Cancer的二维可视化结果。

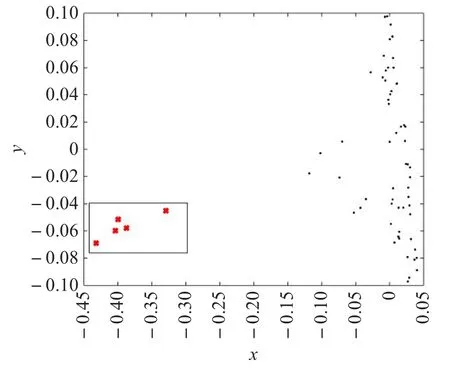
图1 Wine数据集的可视化

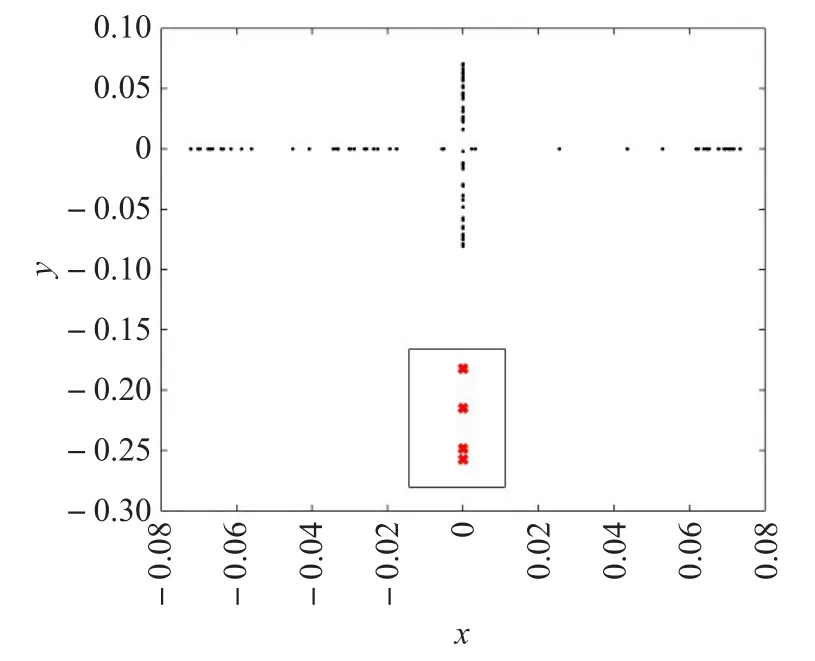
图2 Iris数据集的可视化

图3 Cancer数据集的可视化

其中图1～3中的横轴、纵轴分别表示高维空间中的图像映射到低维空间所对应的横、纵坐标。从图中可以看出，数据集在降至二维空间中后离群点达到了远离了大多数的点的效果。

4.2 与BD方法的对比实验

江峰[3]提出了一种新颖的基于距离与边界的离群点检测方法（BD），对于一个给定的数据集U，X是U的子集。由于BD算法，需要针对每个属性的X不同属性值进行分析，且只检测数据集的一个子集中的离群点，尽管如此，该算法计算量非常大，运行时间非常长。因此本文只对4个数据集进行分析。BD方法只检测X数据集中的离群点，但本文提出的方法，仍然针对表1中前4个数据集，检测其各自的离群点。在BD方法中，设X为表1数据集的前10个点，且离群点分别位于X的前4、5、2、4个位置。针对不同的数据集，设置不同的参数，Zoo数据集进行实验时，OLLE中参数设置为：ε=0.2，ε1=0.003，ρ=1，k=10，Wine、Iris和Cancer数据集的参数设置同4.1节，实验结果如表2，其中括号内为实验运行的时间。

根据表2的实验结果可知：对Iris和Wine数据集，两种方法都准确地检测出离群点，但对于Cancer和Zoo这两个数据集来说，OLLE方法检测离群点的精度明显高于BD方法，且应用OLLE方法实验运行的时间少于BD方法实验运行的时间。

表2 BD与OLLE对比实验

4.3 与LOF和RFSSOD方法的对比实验

LOF和RFSSOD两种方法分别是基于密度和基于聚类的离群点检测方法，它们都是依据近邻点的距离来求密度和聚类的。RFSSOD方法结合了模糊集（FCM）、粗糙集（RCM）和半监督异常知识发现（SSOD）方法进行离群点的挖掘，用到了一部分标记的正常点与离群点来获得较好的聚类结果。RFSSOD主要讨论边界中的点是离群点的可能性，因此缩短了计算的时间。用LOF和RFSSOD两个方法与OLLE进行比对。选取4个维数较高的数据集，其中Wdbc是UCI中的数据集，Optical handwritten和Mnist都是数字数据集，PIE为人脸数据集。在LOF中，8个数据集中的邻域大小k分别为10、10、10、10、20、10、10、20。在RFSSOD中，有三个参数r1、r2、ς，r1、r2是调节参数，调节FRCM、SSOD与标记样本之间的关系。ς为一个阈值，判断样本点属于某一类的下近似，还是属于多个类的上近似。在这里数据的标记信息如表3所示。

表3 数据集描述

在RFSSOD中，三个参数r1,r2,ς在8个数据集的值分别为：

在OLLE中，前四个数据集参数同4.2节，后四个数据集参数设定：

实验结果如表4所示。

根据表4的实验结果可知，前四个数据集，维度相对较低，3种方法均能发现离群点。但对于Wdbc、Minst和PIE这3个数据集，维数相对较高，本文提出的方法的效果较好于其他两种方法。LOF和RFSSOD两种方法分别是基于密度与基于聚类的离群点检测方法，它们都是计算近邻点的距离来进行求密度，聚类的。然而在高维空间中，基于距离的方法不一定是准确的，因为高维数据集中的数据点非常稀疏，根据距离来判断离群点不一定能达到理想的效果，而本文提出的方法是保证数据点的局部几何结构不变，当映射到低维空间中，数据点比较紧凑，就可以在低维空间中进一步检测离群点。因此对于大多数数据集，本文方法的效果都比较好，但对于Optical handwritten据集，RFSSOD方法检测离群点的精度优于OLLE方法，这是由于RFSSOD是一种半监督聚类方法，利用一定的先验知识，因此检测出的离群点的个数较多。但是对数据集进行聚类时，离群点的个数较少时，几乎很难将离群点都聚到一个类中，这是聚类方法常遇到的一个问题。应用三种方法对8个数据集进行实验，其中，有两个数据集OLLE运行的时间最少，有6个数据集RFSSOD算法运行的时间最少。运行时间的长短与数据集的样本数，数据样本的属性个数有关，不同的数据集可能运行的时间不同。

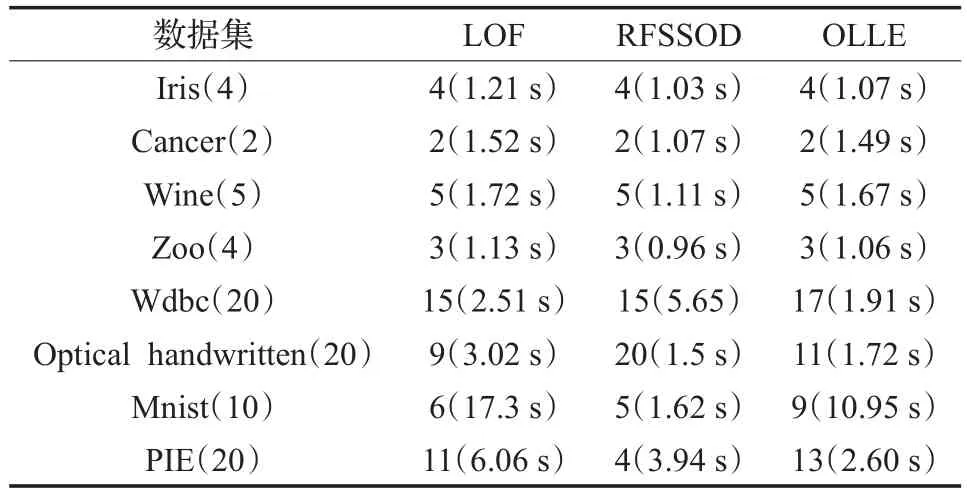
表4 离群点检测结果

4.4 与基于最小生成树的KNN（MST-KNN）方法的对比实验

OLLE是在保持局部几何结构的前提下，将数据集从高维空间降至低维空间，同时让离群点与大多数点远离，并在低维空间中用基于最小生成树的KNN启发式方法（MST-KNN）来进行离群点检测，应用topn1方法，把离群程度最大的几个点判定为离群点。在高维空间中利用MST-KNN检测离群点的精度与OLLE检测离群点的精度进行对比实验。最后都是通过选取离群程度最高的前n1个样本作为候选离群点。在MST-KNN中，对8个数据集，参数k分别设置为10、10、10、10、20、20、10、10。OLLE方法的参数设置同4.3节。实验结果如表5所示。

根据表5的实验结果可知，对Iris、Cancer、Zoo数据集，两个方法均能检测出离群点。但是对其他数据集，用OLLE将数据降维，并在低维中使用MST-KNN方法检测离群点的精度明显多于高维中使用MST-KNN算法来检测离群点的精度。实验证明了OLLE通过降维来发现离群点的方法是合理的。在这几个实验中，OLLE算法运行的时间多于MST-KNN方法运行的时间，这是因为OLLE是将数据降维，然后应用MST-KNN，因此计算时间比MST-KNN稍长。

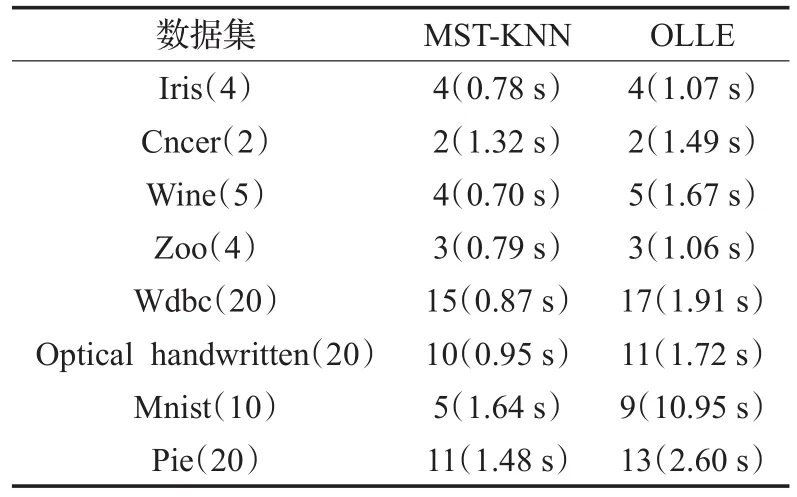
表5 离群点检测结果

5 参数分析

5.1 k的分析

如果k选取太小，离群点的k近邻个数比较少，检测不到离群点。如果k选取太大，不能凸显数据的局部几何结构。如图4，只选取3个有代表的数据集Wine、Wdbc和Mnist进行实验，观察参数k对实验结果的影响，其他几个数据集也有类似的结果。

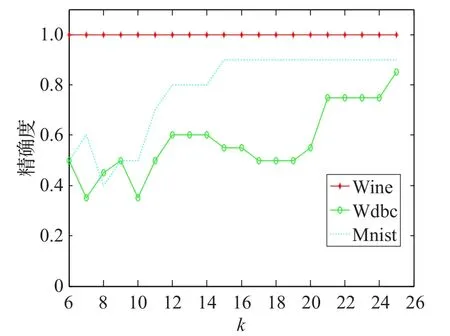
图4 OLLE对不同的数据集，不同的近邻k的分析结果

根据图4可以看出，Wine数据集对k是不敏感的，因为离群点的离群程度比较高，虽然k发生变化，但是都能准确发现离群点。然而对于后两个数据集而言，随着k的变化，发现离群点的精度也在变化。可以看出此OLLE方法发现离群点的精度同样受k的影响，然而，当k在一个小范围内变化时，检测离群点的精度可能是不变的。可以说明OLLE在一定范围内，对k不是非常敏感的。产生这一结果的原因是因为采用了求N(xi)的方法，当k在一定范围变化时，近邻集N(xi)可能是不变的。因此本文提出的方法在一定范围内对参数k是不敏感的。

5.2 d的分析

只选取3个有代表的数据集Mnist、optical handwritten和PIE进行实验，观察参数d对实验结果的影响，其他几个数据集也有类似的结果。在OLLE方法中3个数据集的参数设置同4.3节。

根据图5的实验结果可知：不同的数据集，当映射到不同维数的低维空间时，检测离群点的准确程度也是不同的。d的选取应该与数据集的本征维数有一定的关系，所以在d取不同值时，得到的离群点的准确程度也不同。图5中Wine数据集不受d的影响。但optical handwritten和PIE受d的影响很大，当d在变化时，检测离群点的准确程度也在变化，且均在d=30时，检测离群点的准确程度最高。

图5 OLLE对不同的数据集，不同的维数d的分析结果

5.3 ε参数分析

ε的选取主要作用是区分下近似与边界。如果ε的值较大，可能导致一部分异常点被分到下近似中，这样，就达不到使异常值远离正常点的效果，进而达不到在降维的过程中区分离群点的效果。如果ε的值较小，所有样本点都在上近似中，下近似中没有点，也就达不到下近似中的点保持局部线性结构的效果，进而也达不到很好的降维效果。因此ε的取值，会影响在低维中检测离群点的精确度。

5.4 时间复杂度分析

6 结束语

针对高维空间中数据集存在维数高、数据点稀疏、计算量大和不容易检测异常值这些问题，本文提出了一种基于LLE的高维数据离群点检测方法。OLLE方法是将数据集从高维空间降至低维空间的过程中保持数据的局部几何结构，同时让离群点与大多数点远离，进而在低维空间用基于最小生成树的KNN启发式方法可以较好地检测离群点。且OLLE方法满足高维数据检测离群点的5点要求。本文对8个数据集进行了测试，并选取4个已有方法进行了比对实验，实验结果证明了本文的方法可以有效地检测离群点，并且改进的方法在一定的范围内对k不敏感。参数的选取将是接下来考虑的问题。

[1] Maciá-Pérez F，Berna-Martinez J V，Oliva A F，et al.Algorithm for the detection of outliers based on the theory of rough sets[J].Decision Support Systems，2015，75：63-75.

[2] 江峰，杜军威，眭跃飞，等.基于边界和距离的离群点检测[J].电子学报，2010，38（3）：700-705.

[3] Jiang Feng，Sui Yuefei，Cao Cungen.A hybrid approach to outlier detection based on boundary region[J].Pattern Recognition Letters，2011，32（14）：1860-1870.

[4] Wang Xiaochun，Wang Xiali，Ma Yongqiang，et al.A fast MST-inspired kNN-based outlier detection method[J].Information Systems，2015，48：89-112.

[5] 王敬华，赵新想，张国燕，等.NLOF：一种新的基于密度的局部离群点检测算法[J].计算机科学，2013，40（8）：181-185.

[6] Bai Mei，Wang Xite，Xin Junchang，et al.An efficient algorithm for distributed density-based outlier detection on big data[J].Neurocomputing，2016，181：19-28.

[7] Ha J，Seok S，Lee J S.A precise ranking method for outlier detection[J].Information Sciences，2015，324：88-107.

[8] Xue Zhenxia，Shang Youlin，Feng Aifen.Semi-supervised outlier detection based on fuzzy rough C-means clustering[J].Mathematics and Computers in Simulation，2010，80（9）：1911-1921.

[9] Daneshgar A，Javadi R，Razavi S B S.Clustering and outlier detection using isoperimetric number of trees[J].Pattern Recognition，2013，46（12）：3371-3382.

[10] Jiang Feng，Liu Guozhu，Du Junwei，et al.Initialization of K-modes clustering using outlier detection techniques[J].Information Sciences，2016，332：167-183.

[11] 张小燕，胡昊，苏勇.高维空间中针对离群点检测的特征抽取[J].计算机工程与应用，2012，48（22）：189-194.

[12] 张净，孙志挥，宋余庆，等.基于信息论的高维海量数据离群点挖掘[J].计算机科学，2011，38（7）：148-151.

[13] Ye Mao，Li Xue，Orlowska M E.Projected outlier detection in high-dimensional mixed-attributes data set[J].Expert Systems with Applications，2009，36：7104-7113.

[14] Bhattacharya G，Ghosh K，Chowdhury A S.Outlier detection using neighborhood rank difference[J].Pattern Recognition Letters，2015，60-61：24-31.

[15] Huang Jinlong，Zhu Qingsheng，Yang Lijun，et al.A nonparameter outlier detection algorithm based on natural neighbor[J].Knowledge-Based Systems，2016，92：71-77.

[16] Liu Feng，Zhang Weijie，Gu Suicheng.Local linear laplacian eigenmaps：A direct extension of LLE[J].Pattern Recognition Letters，2016，75：30-35.

[17] Niu Ben，Gu Hongbin，Sun Jin.Weighted kernel locally linear embedding for dimensionality reduction[J].Journal of Information&Computational Science，2014，11（7）：2109-2116.

[18] 吴晓婷，闫德勤.改进的非线性数据降维方法及其应用[J].计算机工程与应用，2011，47（2）：156-159.

[19] Malik Z K，Hussain A，Wu J.An online generalized eigenvalue version of Laplacian Eigenmaps for visual big data[J].Neurocomputing，2016，173：127-136.

[20] 向婷婷，罗运纶，王学松.流形学习及维数约简在数据隐私保护中的应用[J].计算机工程与应用，2011，47（8）：79-82.

DENG Tingquan,LIU Jinyan,WANG Ning.Locally linear embedding method for high dimensional data outlier detection.Computer Engineering andApplications,2018,54（6）：115-122.

DENG Tingquan,LIU Jinyan,WANG Ning

College of Science,Harbin Engineering University,Harbin 150001,China

Due to the fact that data distribution is sparse in the high dimensional space,it can’t achieve desired effect in the high dimensional space by using the conventional methods.This paper proposes an Outlier detection method based on Locally Linear Embedding（OLLE）.In the proposed OLLE method,it establishes an effective rough set model which aims to retain the local lineal structure of samples in the lower approximation.Meanwhile,it constructs two weights to keep the local neighbor structure of all points and guarantee outliers away from normal points when high dimensional points are mapped into a low dimensional space.At last,this paper uses a minimum spanning tree-inspired k-nearest neighbors method to detect the outliers in the low dimensional space.A series of simulation experiments show that the OLLE can better keep the local geometric structure,and outliers are detected effectively in the low dimensional space.

locally linear embedding;dimensionality reduction;high dimensional data;outlier;k-nearest neighbors

由于高维空间中数据点比较稀疏，用传统方法来检测高维空间中的离群点不能达到预期效果。提出了一种基于局部线性嵌入的离群点检测方法（OLLE）。在OLLE降维方法中，建立了一种有效的粗糙集模型，使数据集的下近似中的点保持局部线性结构。同时构造两个权重，使所有样本点保持局部近邻结构，且保证在降维的过程中使离群点远离正常点。最后，在低维空间中，采用基于最小生成树的k-最近邻启发式方法来检测离群点。通过一系列的模拟实验，证明OLLE方法能达到很好的降维效果，并且在低维空间中可以有效地检测出离群点。

局部线性嵌入；维数约减；高维数据；离群点；k-最近邻

2016-10-24

2016-12-14

1002-8331（2018）06-0115-08

A

TP301

10.3778/j.issn.1002-8331.1610-0261

国家自然科学基金（No.11471001）。

邓廷权（1965—），男，博士，教授，研究领域为图像处理、计算机视觉、模式识别、人工智能、数据挖掘；刘金艳（1991—），女，硕士，研究方向为数据挖掘，E-mail：13019003609@163.com；王宁（1992—），女，硕士，研究领域为数据挖掘。