Macro and micro mechanics behavior of granite after heat treatment by cluster model in particle flow code

Wen-Ling Tian·Sheng-Qi Yang·Yan-Hua Huang

1 Introduction

Granite is a very common rock in the earth’s crust[1].It is rich in elements with heat-producing radioactive isotopes,which makes it an important reservoir material for enhanced geothermal systems[2].It is an excellent medium for nuclear waste disposition rock projects due to its lower permeability and better integrity[3]and also a perfect material for geological carbon storage[4].Therefore,many researchers have focused on the mechanics behavior of granite after thermal treatments[5–8]

The work of Glover et al.[9]used acoustic-emission(AE)to monitor the process of thermal cracking as it occurs during heating,and the results show that a strong peak of micro-cracking at the phase transition temperature forquartz(573◦C)was superimposed upon a background of microcracking due to thermal expansion.Then Zhao et al.[10]adopted micro-CT to investigate the granite under different elevated temperatures.It was observed that certain microcracks in the specimens propagated under 200◦C,and the micro-cracks developed and even connected to form larger cracks under 300◦C.A crack net around each granite crystal grain was formed and caused the polygonal grains to be isolated from each other when the heating temperature reached 500◦C.It was also found that 90%of the thermofracturing happened along the weak boundaries between the crystalgrain and the surrounding cement,with less than 10%of the fracturing cracks crossing the grains.Furthermore,Sun et al.[11]found that the granite compressive strength,tensile strength,permeability,and wave velocity have larger change in temperature between 400 and 600◦C,and especially at a temperature of quartzα−βphase transformation.The work of Shao et al.[12]studied the effect of temperature on mechanical behavior of Strathbogie granite under uniaxial conditions.The results show that the failure modes of Strathbogie granite specimens changed from brittle fracturing to quasi-brittle shear fracturing and eventually to ductile failure with increasing temperature.Also,Kumari et al.[13]found that increasing temperature leads to an initial increment with granite strength and shear parameters followed by reduction.This was further confirmed by SEM analysis,according to which the rock micro-structure subjected to only minor change at relatively low temperature and higher temperature causes micro-cracks to develop along the rock mass grain boundaries.

The experiments mentioned previously had greatly improved our understanding of the thermal damage and thermal cracking mechanics in rock,but the micro-mechanics behavior,such as cracks and energy evolution in the failure process,cannot be observed.Therefore,numerical modeling with adequate consideration of rock micro structures is needed to solve this problem[14].To this end,Shao et al.[12]incorporated date of tested specimens into a finite element model so that both plastic and ductile behavior of the Strathbogie granite could be predicted over a wide range of temperature.Furthermore,Yu et al.[15]proposed a micro structure-based numerical model(RFPA-DTM)for the investigation of thermally induced rock mechanics behavior,and found that thermal cracks mostly start at the boundaries between the mineral grain boundaries and propagate along the boundaries to form locally closed polygons.The work of Zhao[16]used PFC2Dto simulate the process of thermally induced micro-and macro-cracks in granite,which elucidates the mechanism response for temperature-dependent mechanics properties.Also,Yang et al.[17]adopted PFC2Dto simulate the Strathbogie granite at high temperature under uniaxial compression,and the peak strength and ultimate failure mode are similar to the experiment.

However,the quartzα–βphase transition cannot be considered in above numerical method.Therefore,in this paper,a cluster model in PFC2Dis used to simulate the grain in the granite specimen.First,the macro mechanical behaviors of granite after different heating treatments under uniaxial compression,such as stress-strain curve,peak strength,elastic modulus,and peak strain are used to verify the feasibility of this method.Then,the micro mechanical behaviors,such as micro-cracking,boundary energy and frictional energy are analyzed in detail.

2 Discrete element modeling method for granite sample under temperature treatment

A parallel bond provides the force-displacement behavior of a finite-sized piece of cementitious material deposited between two balls and does not preclude the possibility of slip.Parallel bonds can transmit both forces and moments between particles.Thus,parallel bonds may contribute to the resultant force and moment acting on the two bonded particles[18].

Granite in nature is composed of irregular grains strongly bonded together.The basic element is a circular disk in PFC2Dconsidering the computational efficiency.However,Jensen et al.[19]and Thomas and Bray[20]suggested that circular disk elements may not adequately model geometry dependent properties such as dilation and interlocking friction.To overcome this shortcoming,clustering the basic disks was suggested.In clustered assemblies,grains are modeled as a group of individual circular disks.The intra-cluster bond strength can be set to different values from the bond strength of inter-cluster[21].The same cluster concept is used in this study to explore how temperature could affect the macromechanical and micro-mechanical behaviors of the granite.PFC2Dcan be used to simulate transient heat conduction and storage in material and develops thermally induced displacements and forces.Thermally induced strains are produced in the PFC2Dmaterial by modifying the particle radius and the force carried in each parallel bond to account for heating of both particles and bonding material.

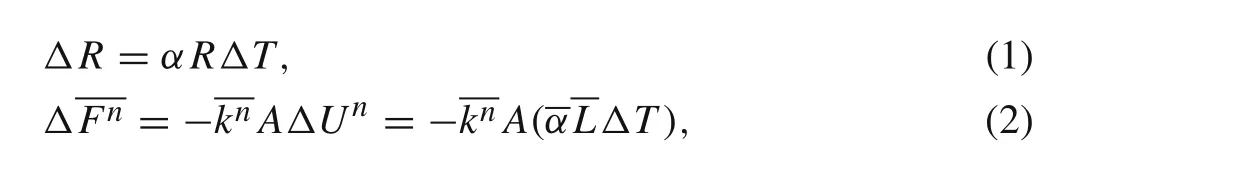
2.1 Numerical specimen

Tested granite specimens have a crystalline and blocky structure.According to the results of X-ray diffraction(XRD),the minerals in the granite material at room temperature are calcite(42.9%),illite(11.4%),biotite(23%),and quartz(22.7%).Figure 1 shows one numerical specimen generated by PFC2D;the scale of this specimen is equal to that of the experimental ones,i.e.dimensions of 80 mm in width and 160 mm in height.Each numerical specimen is assembled by 6008 clusters(grouped by five particles).Based on individual cluster identification code,each cluster is randomly specified to a mineral,the cluster number corresponding to the mineral content,and eventually four mineral group are formed.Thus,2656 clusters are defined as calcite(α=14.0×10−6K−1),608 clusters are defined as illite(α=9.13×10−6K−1),1381 clusters are defined as biotite(α=3.0 × 10−6K−1),and 1363 clusters are defined as quartz(α=24.30×10−6K−1)[22].

2.2 Heating process

The different coefficient of linear thermal expansion is assigned to different minerals before heating.To minimize thermal shocks and development of stress fractures,the temperature of granite specimens is assumed to change uniformly and in a sufficiently short time.The temperature change uniformly by 5◦C every step and cycle the model until the ratio of maximum unbalanced force divided by average force over all particle equal or less to 0.01.The radius expansion with 1.0046[23]is applied to the quartz clusters when the temperature elevated to 573◦C,and the quartz particle radius shrinks with 0.9954 when the temperature decreases to 573◦C.This process can be used to simulate the phase transition of quartz.Ten thousand cycles were operated after reaching the target temperature,and then the same ratio of cooling is applied to the specimen.

Fig.1 Numerical specimen of granite built in PFC2D by cluster model

2.3 Loading

The four walls around the specimen are deleted before heating;therefore,two walls are added to the bottom and top of the specimen as the loading plate after the heating treatment.An external displacement is applied on the two walls in the axial direction to simulate uniaxial loading.To ensure the specimen is at a quasi-static state,a sufficiently low displacement rate(0.05 m/s)is applied.In the simulation process,the software first computes the critical time step and then assigns a reasonable time step.The time step is 3.49×10−8s/step in this paper,which indicates that it requires 572,901,747.4 steps to move 1 mm of the wall.

3 Confirmation for micro-parameters of granite

It is very difficult to determine the micro-parameters by experiment.However,in order to validate the particle properties used in the numerical modeling,it is essential to establish a correlation between the macro-behavior and micro-parameters.During the calibration process,the microparameters are confirmed by using trial and error[24].Table1 lists the micro-parameters used in the PFC2Dmodel for granite specimens in this research.The effective Young’s modulus of the particle and parallel bond are both 25 GPa,and the ratio of normal to shear stiffness of the particle and the parallel bond are both 1.5.The value of the intra-cluster parallel-bond normal and shear strength are 180±30 MPa and 280±60 MPa,respectively.The value of the inter-cluster parallel-bond normal and shear strength are 90±20 MPa and 140±30 MPa,respectively.

Table 1 Micro-parameters of cluster model in PFC2D

3.1 Calibrating micro-parameters by experimental results of granite at room temperature

Figure 2 depicts the comparison between the experimental and numerical failure mode of granite specimen at room temperature under uniaxial compression.As numerical failure mode shown in Fig.2,the red and blue segment represent the tensile and shear micro-crack,respectively.The numerical granite specimen leads to the shear failure mode,which is similar to that obtained by experiment.The peak strength,elastic modulus,and peak strain of numerical failure are 164.72 MPa,51.46 GPa,and 3.98×10−3,respectively,which are approximately equal to those obtained by experiment(i.e.167.76 MPa for peak strength,36.38 GPa for elastic modulus,and 4.77×10−3for peak strain).

3.2 Calibrating micro-parameters by experimental results of granite at elevated temperature

Figure 3 presents a comparison of experimental and numerical stress-strain curves for granite after different temperature treatment under uniaxial compression.According to Fig.3a the stress-strain curves of 25 to 900◦C show two different behaviors.The stress-strain curves of 25 to 450◦C display a sudden drop of stress after peak strength.On the other hand,the curves of temperature over 600◦C display a more gradually decrease in stress after peak strength with increasing axial strain.As presented in Fig.3b;the same behavior of stress-strain after different temperatures appears in the numerical result.The stress-strain curves of granite after increasing temperatures between 25 to 600◦C show a sudden drop of stress after peak strength and display a more gradual decrease with increasing strain over 600◦C.

Figure 4 illustrates the detailed comparison between experimental and numerical uniaxial compressive strength,elastic modulus,and peak strain of granite with different elevated temperatures.The black and red points denote the mechanics parameters of the experiment and numerical simulation,respectively.

From Fig.4a,it is clear that the trend of peak strength with increasing temperature obtained by numerical method is similar to that obtained by experiments.Moreover,the numerical peak strength is similarly equal to that obtained by experiment for the same temperature.When the temperature is below 300◦C,the peak strength is almost constant.Then,the peak strength has a slight decrease when the temperature increases from 300 to 450◦C.However,a sudden drop of peak strength can be observed when the temperature increases from 450 to 600◦C.Finally,the peak strength remains steady over 600◦C.

From Fig.4b,it can be seen that the elastic modulus after heating treatment simulated by PFC2Dhas a similar trend with that obtained by experiment.When the temperature is below 450◦C,the elastic modulus is almost constant.However,there is an obvious drop of elastic modulus can be observed when the temperature increases from450 to 600◦C.The elastic modulus enters a stationary phase when the temperature is over 600◦C.

From Fig.4c,it is clear that the peak strain obtained by numerical method has the same trend as that obtained by experiment after different increasing temperature treatments.When the temperature is below 450◦C,the peak strain displays a slowly increase with temperature.However,an obviously arise of peak strain is observed when the temperature increases from 450 to 600◦C.Finally,the peak strain obtained by numerical simulation increases steady when the temperature is over 600◦C.However,the peak strains obtained by experimentation decrease when temperature increases from 750 to 900◦C.

Fig.2 A comparison between experimental and numerical failure mode under room temperature[25].a Experimental result,b numerical result

Fig.3 Comparison between experimental and numerical stress-strain curves of granite at different temperature under uniaxial compression.a Experimental results[25],b numerical results

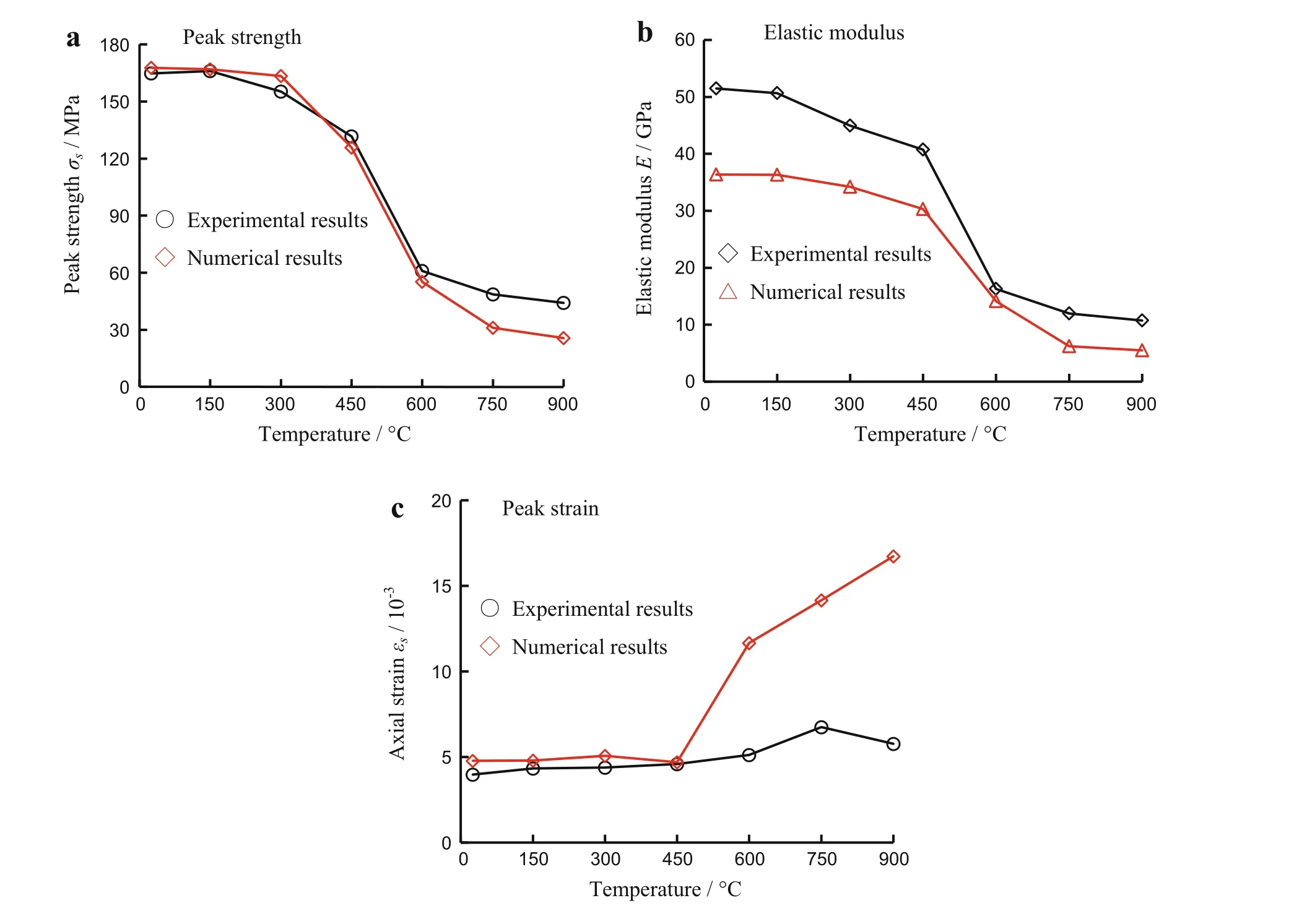
Fig.4 Comparison between experimental and numerical uniaxial compressive strength,elastic modulus and peak strain of granite after different elevated temperature[25].a Peak strength,b elastic modulus,c peak strain

4 Micro-mechanism behavior of granite after elevated temperature

When granite specimens are subjected to a thermal load,thermal damage and thermal cracking usually occur,affecting the mechanical behavior of rock.Therefore,it is significant to understand thermally induced rock damage and thermally cracking mechanisms for both scientific research and engineering application.PFC2Dcode can recognize the number and position of cracks and trace the energy dissipation of the specimen easily.Thus,PFC2Dis used to analyze the crack and energy variation of the granite after increasing different temperatures in this section.

4.1 Micro-crack evolution of granite after thermal treatments

Figure 5 depicts the Micro-crack evolution of granite with increasing temperature.From Fig.5,it is clear that the micro cracks induced by thermal loading are almost tensile crack.When the temperature is below 300◦C,the micro-cracks randomly distributes in the specimen,and do not coalesce with each other.However,the micro-cracks coalesce partially along the inter-granular surfaces when the temperature reaches 450◦C.From Fig.5a–c,it can be seen that the micro-cracks are mainly observed at the boundary of biotite.This causes the linear expansion coefficient of biotite to be less than other minerals,and tensile forces concentrate near biotite easily when granite is under elevated temperature.However,the macro-cracks appear along the inter-granular surfaces when the temperature is up to 600◦C.Because of the macro-crack initiation,tensile force concentration is released,and few new macro-cracks are observed when the temperature is over 750◦C.This phenomenon indicates that the peak strength and elastic modulus of granite remain steady when the temperature over 600◦C.

The evolution of the micro-cracks with increasing temperature obtained by numerical method is similar to that obtained by experimentation.Figure 6 presents thermo-cracking CT of granite under different temperatures.Granite is very compact,and micro-cracking is not observed in the specimen under room temperature.When the temperature increases to 200◦C,a certain number of micro-fissures in the specimen are observed,and the micro-fissures develop and even connect to large fissure under 300◦C.A fissure net around each granite grain is formed and causes the polygonal grains to be isolated from each other when the heating temperature reaches 500◦C[10].

Figure 7 illustrates the influence of temperature on inter granular and intra-granular cracking of granite after heating treatment.From Fig.7,we can see that a small number of cracks are observed in the specimen when the temperature is below 150◦C;only 75 inter-granular cracks are observed in the specimen when the temperature goes up to 150◦C.However,an obvious rise of inter-granular cracking,intra-granular cracking,and the ratio of intra-granular and inter-granular is observed when the temperature increases from 150 to 600◦C.Then,the inter-granular cracking,intra granular cracking,and intra/inter-ratio enter a stationary increase phase when the temperature is over 600◦C.These results can be explained by the fact that macro-cracking appeared to lead to some micro-crack generation with increasing temperature.The ratio between intra-granular and inter-granular cracking increases with the temperature when the temperature is over150◦C,but the maximum ratio is less than 12%;this result is similar to that obtained by Ref.[10].

Figure 8 presents an average-width micro-crack after different high temperatures.Unlike variation of the crack number with temperature,average width of the cracks in granite is near zero when the temperature is below 300◦C.However,the average width of cracks steadily increase with temperature when the temperature is over 300◦C.

Fig.5 Micro-crack evolution of granite with increasing temperature.a T=150 ◦C,b T=300 ◦C,c T=450 ◦C,c T=300 ◦C,d T=500 ◦C,e T=750 ◦C,f T=900 ◦C

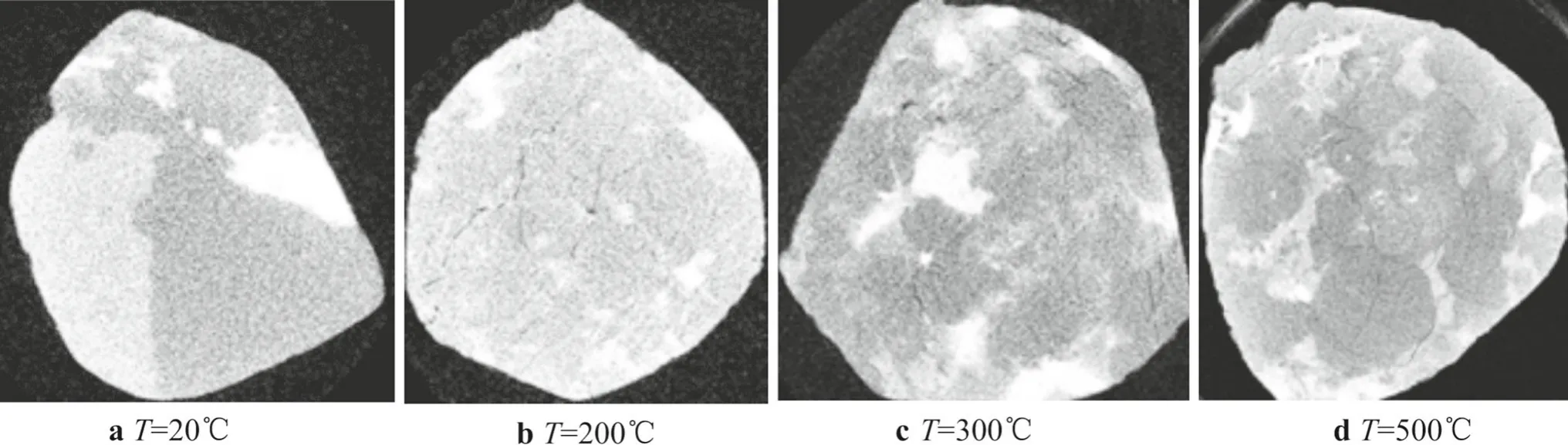
Fig.6 Thermo-cracking CT sections of granite under different temperatures[10].a T=20 ◦C,b T=200 ◦C,c T=300 ◦C,d T=600 ◦C

Figure9 illustrates evolution of micro-crack numbers with granite temperature after heat treatment(T=900◦C).Micro-cracking is almost zero when the temperature is below 150◦C.Then,the curve of micro-crack number shows a nonlinear increase with temperature when the temperature increases from 150 to 300◦C and to a linear increase phase when the temperature ranges from 300 to 573◦C.Microcracks have a sharp increase when the temperature is up to 573◦C due to the phase transitionα–βof quartz.However,the increased rate of micro-cracking becomes smaller when the temperature varies from 573 to 900◦C.The micro-crack number is almost constant when the temperature decreases from 900◦Cto room temperature,except for the temperature of quartz phase transitionβ-α(573◦C).

Figure 10 presents crack count variation of granite specimens during the whole deformation failure with respect to different temperatures.In Fig.10,the crack counts mean the crack increment in every 100 steps.The crack count variation with axial strain is the same as AE count variation with time,which can explain the failure process and crack evolution mechanism of granite.When the temperature is below 300◦C,as illustrate in Fig.10a–c,the crack characteristics of granite can be divided into two typical periods,a quiet period and active period.In the quiet period,the cracks are almost zero.In the active period,the stress-strain curves of the granite specimen undergo two different stages,i.e.the stage of stable crack propagation,and the stage of unstable crack propagation.The stage of stable crack propagation corresponding to elastic deformation and crack counts are also less compared to the stage of unstable crack propagation.The stage of unstable crack propagation corresponding to the stress–strain curve is near the peak strength,which is accompanied by a large crack count increase.

When the temperature ranges from 450 to 600◦C,as show in Fig.10d,e,the crack characteristics of granite also can be divided into two typical periods,a quiet period and active period.However,the crack counts concentration in the active period become weaker with increasing temperature.Thus,the active period cannot be divided into the stage of stable and unstable crack propagation when the temperature is up to 600◦C.The axial stress corresponding to the end of the quiet period becomes smaller when the temperature increases from 300 to 600◦C.It can be explained that the structure becomes looser when the granite treated by a heat-ing and cooling cycle,and cracks start easily when loading axial stress.

Fig.7 Influence of temperature on inter-granular and inter-granular crack of granite after heating treatment

Fig.8 Average width of micro-crack after different high-temperature treatments

Fig.9 Crack number evolution with temperature

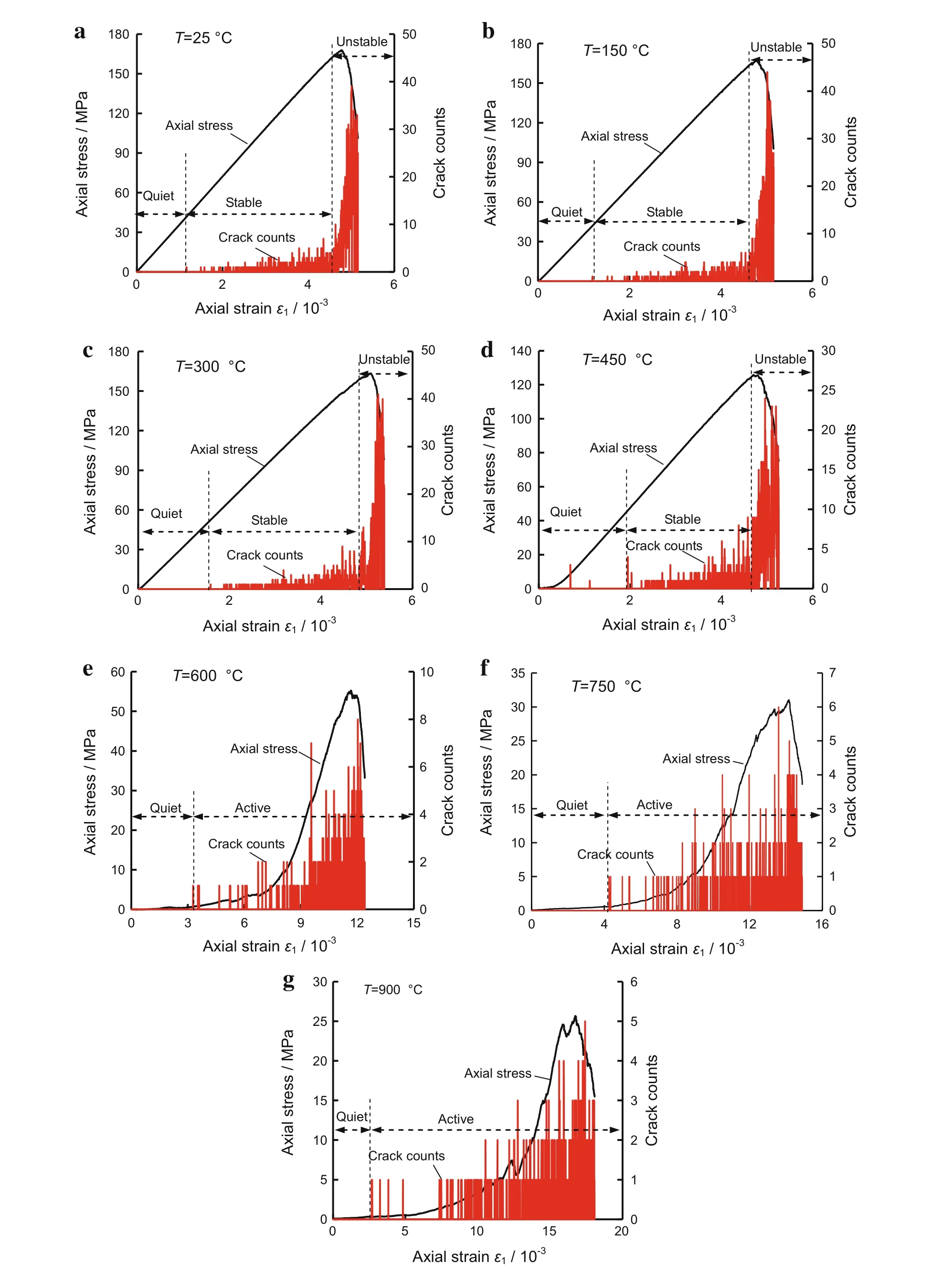
Fig.10 Crack count variation of granite specimens during the whole deformation failure with respect to different temperatures.a T=25◦C,b T=150 ◦C,c T=300 ◦C,d T=450 ◦C,e T=600 ◦C,f T=750 ◦C,g T=900 ◦C

Same as the granite specimen atT=600◦C,granite after heat treatment of 750 to 900◦C also has a quiet period and active period,as shown in Fig.10f,g.No larger crack counts are observed in the active period of the granite specimen at 600 to 900◦C,and the crack number of the granite specimen is very active during the whole active period.This phenomenon indicates that the cracks induced by high temperature damage the structure of the granite,which leads to the capacity of storing strain energy becoming weaker.Thus,the stress–strain curve displays a more gradual decrease with increasing strain.

Figure 11 depicts the evolution of accumulated crack counts for granite specimens after different thermal treatments.From Fig.11,it can be seen that the evolution of accumulated crack counts for granite specimens become slower with increasing temperature when the temperature ranges from 450 to 900◦C.However,the accumulated crack counts for all granite specimens increase slowly with the increase of axial strain,followed by a sharp increase,which agrees very well with an exponential increase.Following this analysis we can recognize that this trend is similar to that obtained by experiments[3].

Fig.11 Evolution of accumulated crack counts for granite after different thermal treatments

4.2 Energy evolution of granite after thermal treatments

Figure 12 presents evolution of boundary and frictional energy for granite specimens after thermal treatments during the whole deformation failure.Because the energy evolution curve of granite atT=150–300◦C is very similar to that atT=25◦C,and atT=750◦C is similar to that atT=900◦C,we only present the curves of granite at 25◦C,450◦C,600◦C,and 900◦C.Boundary energy indicatestotal accumulated work done by all walls on the assembly;frictional energy indicate total energy dissipated by frictional sliding at all contacts

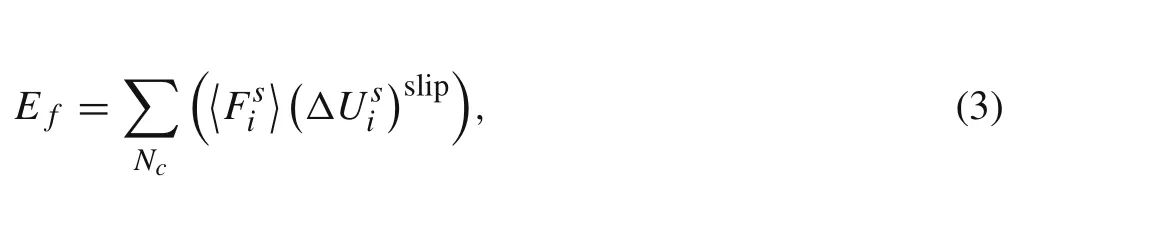
Boundary energy variation with axial strain agrees well with a square-law increase.Frictional energy of granite in creases slowly with the increase of axial strain,followed by a sharp increase,which agrees very well with an exponential increase.AtT=25◦C,as shown in Fig.12a,the boundary energy has a square-law increase in the whole deformation failure.Frictional energy increases slowly with the increase of axial strain before peak strength point and then sharply increases after peak strength.This phenomenon indicates that the displacement between clusters increases after peak strength,then frictional energy is produced by movement between particles.

AtT=450◦C,as shown in Fig.12b,boundary energy also increases in the square way,and the magnitude of boundary energy less than that atT=25◦C.Frictional energy of granite before peak strength become more comparing with that atT=25◦C.Then,frictional energy sharply increases after peak strength.AtT=600◦C,as shown in Fig.12c,frictional energy almost equals the boundary energy before axial strain below 5×10−3,which means almost all boundary energy is translated to frictional energy,and no strain energy is stored.Frictional energy increases exponentially in the whole deformation failure.AtT=900◦C,as shown in Fig.12d,the boundary energy and frictional energy variation with axial strain same as that atT=600◦C.However,the difference between boundary energy and frictional energy becomes smaller than that belowT=600◦C.

From Fig.12,we can see that increasing boundary energy is translated to frictional energy at initiation loading stage with increasing temperature.This phenomenon indicates that the granite specimen become looser with increasing temperature,the displacement between clusters caused by structure adjustment increases,and then more frictional energy is produced.

Figure 13 illustrates boundary energy and frictional energy variation with temperature for granite specimens at peak strength point.Boundary energy is almost constant when the temperature is below 300◦C and sharply decreases when the temperature increases from 300 to 600◦C,then enters a stationary phase again when the temperature is over 600◦C.Frictional energy increases gradually with the increase of temperature in general,which increases from 176 to 438 N·m as the temperature increases from 25 to 900◦C.The ratio between frictional energy and boundary energy shows a progressive increase with increasing temperature.At room temperature,the ratio was about 0.034,which then increases to 0.309 and 0.357 at 750◦C and 900◦C,respectively.The change of ratio represented a modest trend in 450◦C,but increased dramatically from 450 to 900◦C.

The increment of the ratio between frictional energy and boundary energy indicates that displacement between grains becomes easier with increasing temperature.The decline of boundary energy indicates that the capacity to store strain energy become weaker with increasing temperature.The strain energy decreasing means that less damage is caused while the strain energy releases after peak strength.The increment of ratio between frictional energy and the decline of boundary energy co-lead plasticity after peak strength of granite after elevated temperature.

Fig.12 Evolution of boundary and frictional energy for granite after different thermal treatments during the whole deformation failure.a T=25 ◦C,b T=450 ◦C,c T=600 ◦C,d T=900 ◦C

Fig.13 Boundary energy and frictional energy variation with temperature for granite specimens at peak strength point

5 Conclusion

To investigate the thermal damage and failure mechanical behavior of granite,a systematic numerical simulation using a cluster model in particle flow code was adopted to analyze the micro-crack distribution and energy evolution of granite after heat treatment(25–900◦C).Through the numerically simulated results,the following conclusions can be summarized.

(1)Based on individual cluster identification code,each cluster is randomly specified to a mineral,which is assigned a corresponding coefficient of linear thermal expansion.In accordance with the experimental results of granite under room temperature, the micro-parameters of cluster model in particle flow code are firstly confirmed.Then granite specimens after heating treatment are tested in numerical simulation,and the results agree well with those obtained by experimentation.The axial stress–strain curve,the peak strength,the elastic modulus,and the peak strain are put forward to discriminate the rightness and reason ability of the numerical simulated method.

(2)When the temperature is below 300◦C,the microcracks are randomly distributed in the specimen.Partial micro-crack coalescence occurs along the inter-granular surface,when the temperature reaches 450◦C.However,the macro-cracking appears along the inter-granular surface,when the temperature is up to 600◦C,and few new macro-cracks are observed when the temperature is over 750◦C.

(3)A small number of cracks are observed in the specimen when the temperature is below 150◦C.However,a significant increase of inter-granular cracking,intra-granular cracking,and ratio of intra-granular and inter-granular is observed when the temperature increases from 150 to 600◦C.Then,the inter-granular cracking,intra-granular cracking,and intra/inter ratio enter a stationary increase phase when the temperature is over600◦C.However,the average width of a micro-crack increases with increasing temperature when the temperature is over 300◦C.The micro-crack number is almost constant when the temperature decreases from 900◦Cto room temperature,except for temperature of quartz phase transitionβ–α(573◦C).(4)Once the granite specimen contain thermally induced cracks,the fracture evolution process is obviously affected by these cracks,especially at 600–900◦C,which do not have larger crack counts in the failure process,and the evolution of accumulated crack counts for granite specimens becomes slower.

(5)Elevated temperature leads to the displacement between granular become easily and the capacity to store strain energy become weaker.These results correlate with plasticity after peak strength of granite after heat treatment.

AcknowledgementsThe project was supported by the National Natural Science Foundation of Jiangsu Province of China for Distinguished Young Scholars(Grant BK20150005)and the Fundamental Research Funds for the Central Universities(China University of Mining and Technology)(Grant 2014XT03).We also would like to express our sincere gratitude to the editor and two reviewers for their valuable comments,which have greatly improved this paper.

1.Shao,S.,Wasantha,P.L.P.,Ranjith,P.G.,et al.:Effect of cooling rate on the mechanical behavior of heated Strathbogie granite with different grain sizes.Int.J.Rock Mech.Min.Sci.70,381–387(2014)

2.Baisch,S.,Weidler,R.,Vörös,R.,et al.:Induced seismicity during the stimulation of a geothermal HFR reservoir in the Cooper Basin.Aust.Bull.Seismol.Soc.Am.96,2242–2256(2006)

3.Yang,S.Q.,Ranjith,P.G.,Jing,H.W.,et al.:An experimental investigation on thermal damage and failure mechanics behavior of granite after exposure to different high temperature treatments.Geothermics 65,180–197(2017)

4.Rutqvist,J.:The geomechanics of CO2storagein deep sedimentary formations.Off.Sci.Tech.Inf.Tech.Rep.30,525–551(2011)

5.Homand-Etienne,F.,Houpert,R.:Thermally induced microcracking in granites:characterization and analysis.Int.J.Rock Mech.Min.Sci.Geomech.Abstr.26,125–134(1989)

6.David,C.,Menéndez,B.,Darot,M.:Influence of stress-induced and thermal cracking on physical properties and microstructure of La Peyratte granite.Int.J.Rock Mech.Min.Sci.36,433–448(1999)

7.Menéndez,B.,David,C.,Darot,M.A.:Study of the crack network in thermally and mechanicsly cracked granite samples using confocal scanning laser microscopy.Phys.Chem.Earth Part A Solid Earth Geod.24,627–632(1999)

8.Chaki,S.,Takarli,M.,Agbodjan,W.P.:Influence of thermal damage on physical properties of a granite rock:porosity,permeability and ultrasonic wave evolutions.Constr.Build.Mater.22,1456–1461(2008)

9.Glover,P.W.J.,Baud,P.,Darot,M.,et al.:α/βphase transition in quartz monitored using acoustic emissions.Geophys.J.Int.120,775–782(1995)

10.Zhao,Y.S.,Meng,Q.R.,Kang,T.L.,et al.:Micro-CT experimental technology and micro-investigation on thermal fracturing characteristics of granite.Chin.J.Rock Mech.Eng.27,28–34(2008)

11.Sun,Q.,Zhang,Z.Z.,Xue,L.,et al.:Physico-mechanics properties variation ofrock with phase transformation under high temperature.Chin.J.Rock Mech.Eng.32,935–942(2013).(in Chinese)

12.Shao,S.,Ranjith,P.G.,Wasantha,P.L.P.,et al.:Experimental and numerical studies on the mechanics behaviour of Australian Strathbogie granite at high temperatures:an application to geothermal energy.Geothermics 54,96–108(2015)

13.Kumari,W.G.P.,Ranjith,P.G.,Perera,M.S.A.,et al.:Mechanics behaviour of Australian Strathbogie granite under in-situ stress and temperature conditions:an application to geothermal energy extraction.Geothermics 65,44–59(2017)

14.Ghassemi,A.:A review of some rock mechanics issues in geothermal reservoir development.Geotech.Geol.Eng.30,647–664(2012)

15.Yu,Q.L.,Ranjith,P.G.,Liu,H.Y.,et al.:A micro structure-based damage model for thermal cracking analysis and application in granite atelevated temperatures.Rock Mech.Rock Eng.48,2263–2282(2015)

16.Zhao,Z.:Thermal influence on mechanics properties of granite:a microcracking perspective.Rock Mech.Rock Eng.49,747–762(2016)

17.Yang,S.Q.,Tian,W.L.,Ranjith,P.G.:Failure mechanical behavior of Australian strathbogie granite at high temperatures:insights from particle flow modeling.Energies 10,756(2017)

18.Itasca Consulting Group,Inc.:PFC2D,v.3.10.Minneapolis,MN(2003)

19.Jensen,R.P.,Bosscher,P.J.,Plesha,M.E.,et al.:DEM simulation of granular media–structure interface:effects of surface roughness and particle shape.Int.J.Num.Anal.Meth.Geomech.23,531–47(1999)

20.Thomas,P.A.,Bray,J.D.:Capturing nonspherical shape of granular media with disk clusters.J.Geotech.Geoenviron.Eng.125,169–78(1999)

21.Cho,N.,Martin,C.D.,Sego,D.C.:A clumped particle model for rock.Int.J.Rock Mech.Min.Sci.44,997–1010(2007)

22.Fei,Y.:Thermal expansion.In:Mineral Physics and Crystallography:AHandbook of Physical Constants,29–44.AGU,Wasington,DC(1995)

23.Carpenter,M.A.,Salje,E.K.H.,Graeme-Barber,A.:Spontaneous Strain as a Determinant of Thermodynamic Properties for Phase Transitions in Minerals.Eur.J.Miner.10,621–691(1998)

24.Zhang,X.P.,Wong,N.Y.:Cracking processes in rock-like material containing a single flaw under uniaxial compression:a numerical study based on parallel bonded-particle model approach.Rock Mech.Rock Eng.45,711–737(2012)

25.Huang,Y.H.,Yang,S.Q.,Tian,W.L.,et al.:Physical and mechanical behavior of granite containing pre-existing holes after high temperature treatment.Arch.Civil Mech.Eng.17,912–925(2017)