A simple algorithm to improve the performance of the WENO scheme on non-uniform grids
Wen-Feng Huang·Yu-Xin Ren·Xiong Jiang
1 Introduction
In solving engineering problems with complicated geometries and broad ranges of flow scales,it is necessary to apply high resolution schemes on non-uniform meshes.Traditional high order finite difference schemes[1–4]which are developed on uniform grids can be applied on curvilinear gridsthrough coordinate transformations[5].The curvilinear grids need not be uniform,but should be sufficiently smooth[6]in physical space.Finite difference schemes on nonuniform Cartesian grids are straightforward to design[7–11],however these schemes cannot be applied directly to curvilinear coordinates.Finite volume schemes are more robust and flexible on non-uniform and curvilinear structured grids and a number of finite volume schemes have been applied to non-uniform Cartesian grids[12,13],curvilinear grids in computational space[14],and non-uniform curvilinear grids in physical space,without coordinate transformations[15–17].
In this paper,we are interested in efficient implementation of finite volume weighted essentially non-oscillatory(WENO)schemeson non-uniformgrids.The WENOs cheme proposed by Liu et al.[18]was significantly improved by Jiang and Shu[19].In the present paper,the latter WENO scheme[19]is denoted as WENO-JS.WENO-JS can be take finite difference or finite volume form.In the present paper,only the finite volume form is considered.Theoretically,it is straightforward to derive the WENO-JS scheme on nonuniform grids.However,it is far from trivial to apply the non-uniform grid WENO schemes.The WENO schemes on non-uniform grids were studied in Refs.[20–24].Specifically,Wang et al.[20]derived the explicit formulations of the fifth-order WENO-JS scheme on non-uniform grids.Since the WENO scheme is nonlinear,the weights must be computed at all cell interfaces in every time step.On non-uniform grids,the evaluation of very complicated weight functions would be very time consuming.If the mesh size-related coefficients are stored,the storage required can be prohibitively large.Therefore,in practical applications,WENO schemes designed for uniform grids are used in most cases.The central WENO scheme[21]is very efficient on non-uniform grids,but requires very large storage.It is observed in the present paper that on certain non-uniform grids,the use of a WENO-JS scheme designed for uniform grids can lead to large errors.Therefore,it is necessary to design efficient WENO schemes that can be readily applied to non-uniform grids.
In the present paper, a very simple technique is proposed to improve the performance of WENO schemes on non-uniform grids.The resulting WENO scheme is denoted as WENONM(modified WENO scheme on non-uniform grid).To ease the presentation,the WENO-JS scheme designed for the uniform grids is still denoted as WENO-JS,and the WENO scheme designed on non-uniform grids[20]is called WENO-N.The WENO-NM scheme is based on the observation that on each candidate stencil of WENO-JS(on a uniform grid),the inter facial value of the dependent variable and the smoothness indicator can be expressed in terms of the cell average of the central cell and its left and/or pseudo interfacial states.The pseudo interfacial state is computed by a certain linear reconstruction of the dependent variable.Since the linear reconstruction can be carried out straightforwardly on both uniform and non-uniform grids,this observation leads to a very simple form of the WENONM scheme where the pseudo interfacial states are evaluated by the linear reconstructions on non-uniform grids.Compared with WENO-N,the WENO-NM scheme is several times more efficient.In addition,WENO-NM is computationally as efficient as WENO-JS,but more accurate than WENO-JS on non-uniform grids.In fact,on arbitrary nonuniform grids,WENO-NM is at least second order accurate,whereas the WENO-JS is only first-order accurate.On uniform or sufficiently smooth grids,WENO-NM reduces to WENO-JS and can achieve a fifth-order of accuracy.This approach is quite general;several improved WENO schemes such as WENO-SYMBO(symmetric bandwidthoptimized WENO)[25],WENO-Z(an improved WENO scheme presented by Borges et al.[26]),and MDCD(minimized dispersion and controllable dissipation)[27,28]schemes can also use this technique to account for the grid non-uniformity.
The remainder of this paper is organized as follows.In Sect.2,the fifth-order finite volume WENO scheme presented by Jiang and Shu[19]is reviewed,and an implementation of modified fifth-order finite volume WENO-NM is proposed.In Sect.3,some numerical tests are presented to demonstrate the performance of WENO-NM.Finally,the concluding remarks are given in Sect.4.
2 The design of WENO-NM
2.1 WENO scheme of Jiang and Shu[19]
The fifth-order WENO method of Jiang and Shu[19](WENO-JS)in a finite-volume framework is described in the context of the scalar,one-dimensional advection equation

wheref=a u.The integration form of Eq.(1)in the control volumeIi=[xi−1/2,xi+1/2]on uniform grids with grid spacingh= (xi+1/2 −xi−1/2)can be written as

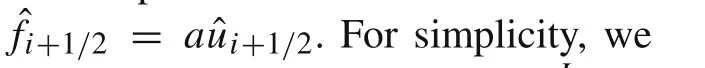
In the fifth-order WENO-JS method on uniform grids,there are three candidate stencils,as shown in Fig.1.For clarity,thei-th cell is denoted asIi.The three candidate stencils are,respectively,S0={Ii−2,Ii−1,Ii},S1={Ii−1,Ii,Ii+1},S2={Ii,Ii+1,Ii+2}.The interfacial states obtained by the reconstruction in terms of the corresponding candidate stencils are


Fig.1 Candidate stencils Sk in the WENO-JS method

Table 1 Optimal weights Ck
and the corresponding smoothness measuresISrare

The final reconstruction polynomial is

In Eq.(6),the weightωkfor the stencilISkis defined by
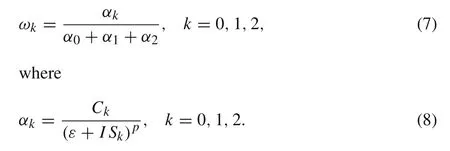
Hereε=10−6andp=2 are recommended,and the coefficientsC kare given in Table.
2.2 Modified WENO method on a non-uniform grid
In this subsection,the design of the WENO-NM scheme will be presented in detail.The WENO-NM scheme is a modification of the WENO-JS scheme that accounts for grid non-uniformity.It is observed in Eqs.(4)and(5)that for every candidate reconstruction,the interfacial value of the dependent variable and the corresponding smoothness indicator depend on the cell averages of three consecutive cells.For example,on stencilS2,the interfacial state and its smoothness measure on a uniform grid are
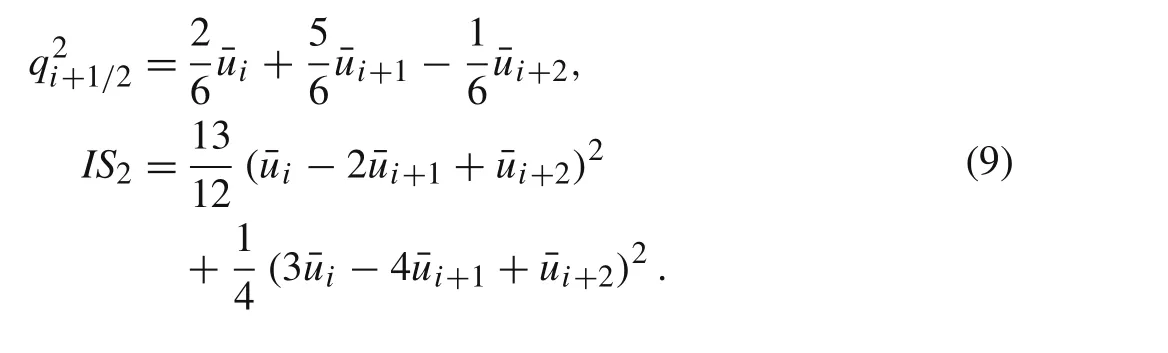
The central cell of this stencil isΩi+1=[xi+1/2,xi+3/2].It is straightforward to show that Eq.(9)can be rewritten as

Equation(10)is just a reformulation of the WENO-JS scheme.It is important to observe that the interfacial valueq2i+1/2can be written as the linear combination of the cell average ofΩi+1and the left/right pseudo interfacial states ˜u i+1/2and˜u i+3/2ofΩi+1.˜u i+1/2and˜u i+3/2are called the pseudo interfacial states because they are just the arithmetic averages of the cell averages of the left and right control volumes,instead of the real interfacial states determined by the reconstruction.

In the same way,the modified interfacial state and the smoothness measure on stencilS1can be written in terms of the cell average and left/right pseudo interfacial states of central cellΩi
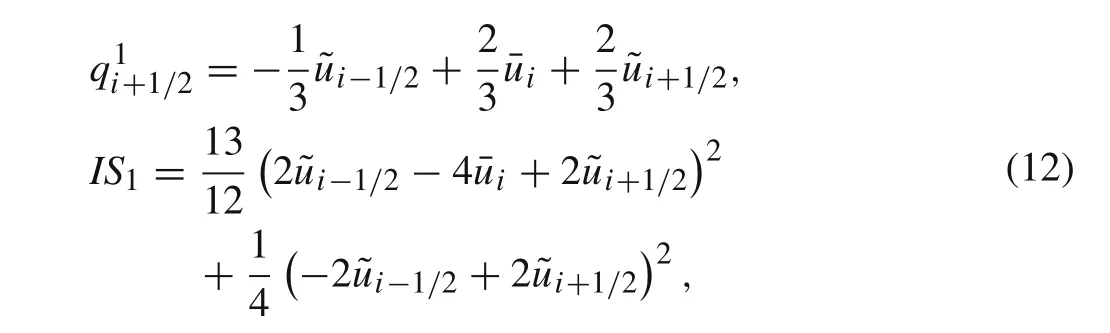
and the pseudo interfacial states are computed with the linear reconstructions on a non-uniform grid.
On stencilS0,the interfacial state and the smoothness measure on a uniform grid are
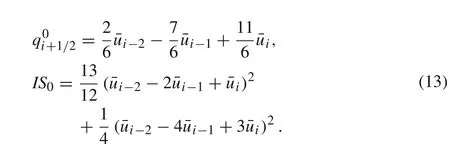
Using the same technique as the modifications ofS2andS1,the result is

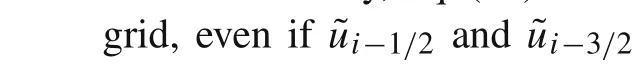
To solve this problem,it is proposed in present paper to rewrite Eq.(14)into
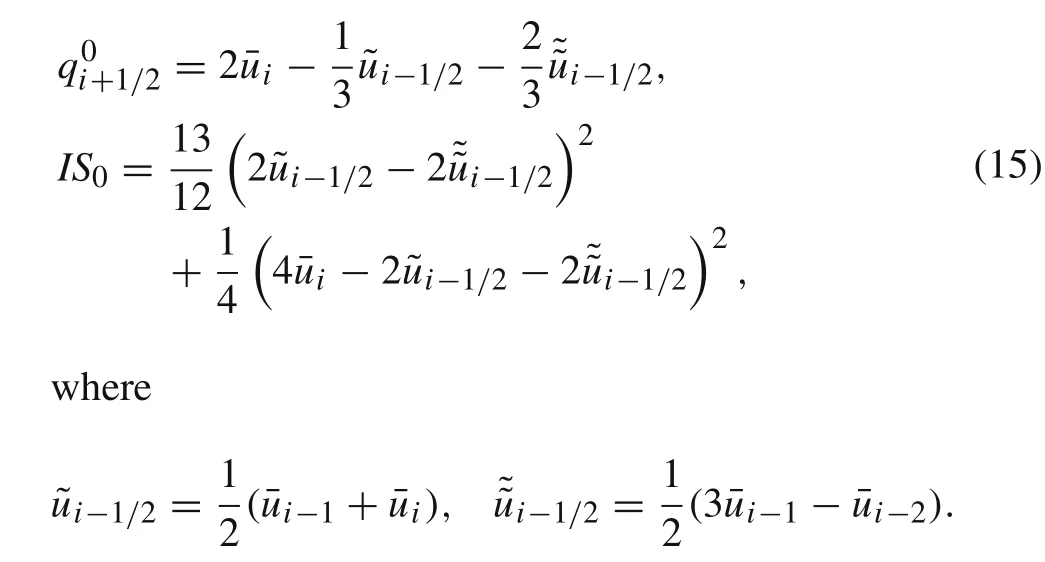

The final reconstructed interfacial state of WENO-NM is

Hereε,p,and the coefficientsCkare the same as WENO-JS.
In summary,the mechanism of the present scheme to account for grid non-uniformity is as follows.To compute the interfacial state at interfacei+1/2,all reconstructions and smoothness indicators are rewritten in terms of the information defined on cellΩiorΩi+1,of which the interfacei+1/2 is the left or right end point.With this reformulation,all stencils of reconstructions are reduced to only one cell(ΩiorΩi+1).Additional information on the original formulations is transformed to the pseudo interfacial states.Therefore,as long as the grid non-uniformity can be accounted for using linear reconstructions for non-uniform grids,WENO-NM can be applied.The WENO-NM reconstruction will be the same as WENO-JS reconstruction when the grid is uniform.This kind of modification can be applied to other optimized WENO schemes[25,26,29–31]and WENO-kind schemes[27,28]on non-uniform grid since the modification does not change the linear weights and non-linear weights.It is straight forward to extend the WENO-NM scheme to the cases of Euler and Navier–Stokes equations.When applied the WENO-NM to multi-dimensional cases,the reconstructions is carried out in a dimension split manner,which is widely used in practical applications.In this case,the mesh size is defined as the distance between the centers of the cell interfaces of a cell in the same coordinate direction.In the present paper,the Riemann solver of Roe is used to compute the inviscid fluxes,and the viscous fluxes are computed using the central scheme.
3 Numerical results
In this section,several benchmark numerical test cases are computed to analyze the behavior of the WENO-NM scheme proposed in the present paper.Since WENO-NM and WENO-JS are the same on uniform grids,we analyze their performances only on non-uniformgrids.In one-dimensional tests,the classical fifth-order Runge–Kutta scheme is used for temporal discretization,and the third-order TVD Runge–Kutta scheme is used in multi-dimensional tests.
3.1 Transportation of a wave packet
This test case is solved to test the accuracy of the WENONM scheme on non-uniform grids.The governing equation is the scalar linear advection equation,which is

WENO-NM is compared with WENO-JS on two types of grids.The first type of grid(GRID-I)is an alternately distributed grid with alternating large and small cells.The second type of grid(GRID-II)is a stretched grid,which is generated by software and usually used in boundary layers.
GRID-I is defined by
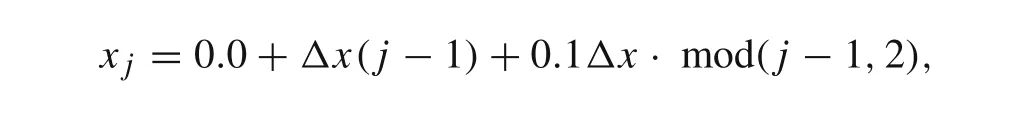
whereΔx=1/(N−1).Nis the number of grid points.The grid length of GRID-II reduces gradually from the beginning of the domain until the middle of the domain and then increases until the end of the domain,so that it maintains periodicity at the boundary.
The numerical errors in terms ofL2norm are shown in Table 2 on GRID-I with different grid sizes.Neither WENONM nor WENO-JS can achieve fifth-order.TheL2error of WENO-NM is much smaller than that of WENO-JS,and WENO-NM still has second-order accuracy.TheL2errors on GRID-II are shown in Table 3.With the grid number increasing,WENO-JS and WENO-NM both achieve fifthorder,and theL2error of WENO-NM is smaller than that of WENO-JS.Figure 2 shows the efficiencies of WENO-JS and WENO-NM.The computations are carried out tillt=100 on GRID-II,and the correspondingL2errors and CPU time are plotted in Fig.2.It is clear that WENO-NM is a better choice in computation.

Table 2 The L2 error on GRID-I

Table 3 The L2 error on GRID-II
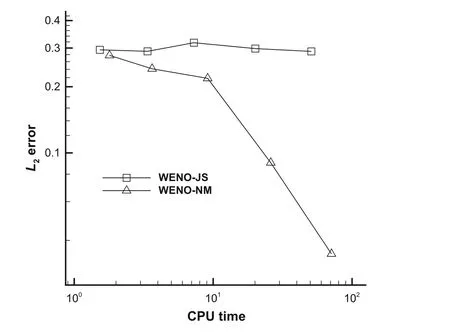
Fig.2 Comparisons of efficiency for WENO-JS,WENO-NM
3.2 Shu–Osher problem
This problem is governed by one-dimensional Euler equations with the following initial conditions

The Shu–Osherproblem describes a Mach 3 right-moving shock wave interacting with a sine entropy wave which generates a flow field with both small scale structures and discontinuities.The computational domain isx∈[0,10]and the advanced time is up tot=1.8 with the Courant numberC F L=1.0.The grid used in the simulation consists of 501 points with non-uniform distribution.The grid points are randomly distributed with the grid size ratio changing between 1 and 4.The numerical solution obtained by the WENO-JS scheme using 20,000 cells on a uniform grid is considered as the “exact”solution.Density distributions are shown in Fig.3 and the CPU time costs by the four schemes are listed in Table 4.The resolution of WENO-NM is close to WENON and CWENO5 and is much better than WENO-JS,and the CPU time cost by WENO-NM is much smaller than that of WENO-N.According to these comparisons,WENO-NM is a better choice on non-uniform grids.The CWENO5 is slightly more efficient than the present WENO-NM scheme.However,the CWENO5 scheme requires much larger storage than the presentscheme.In the one-dimensional case,52 coefficients need to be stored for each cell.
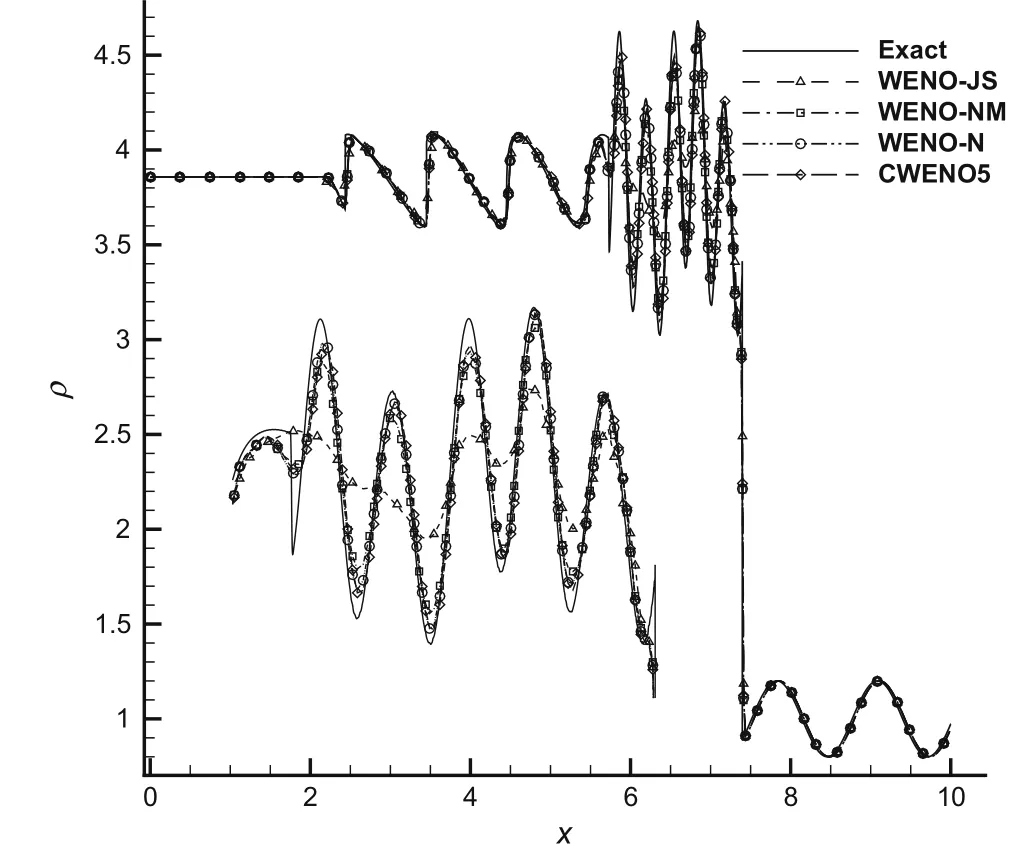
Fig.3 Shu–Osher problems.Distribution of density at t=1.8 s

Table 4 CPU times for Shu–Osher problem
3.3 Isentropic vortex problem
The isentropic vortex transport problem is used to examine the performance of the modified WENO scheme on nonuniform Cartesian and curvilinear grids.The computational domain is[0,10]×[0,10].The mean flow is(ρ,u,v,p)=(1,1,1).An isentropic vortex is added to the mean flow with the following perturbations
where(¯x,¯y)=(x−5,y−5),r2=¯x2+¯y2and the vortex strength isχ=5.The numerical solution is output at timet=10,and the Courant number isC F L=1.0 for all the tests.
There are three types of grid used in the numerical simulations.The first type(Fig.4a)is a randomly distributed Cartesian grid(ALT-RAND);The second type(Fig.4b)is a stretched Cartesian grid which is usually used in boundary layer simulation(STRETCHED);The third type(Fig.4c)is a distorted wavy grid(DIS-RAND).There are 81 points in theiandjdirections,respectively,for all grids.
The randomly distributed Cartesian grid(ALT-RAND)is defined by

Fig.4 Three types of grid used for isentropic vortex.a ALT-RAND,b STRETCHED,c DIS-RAND


Fig.5 Density contour on ALT-RAND grid at t=10 s.30 equally spaced contour lines from 0.55 to 0.95.a WENO-JS,b WENO-NM,c WENO-N

Table 5 CPU times and L2 errors on ALT-RAND grid
whereΔx=L x/(N−1),Δy=L y/(N−1).L xandL yare the lengths of the domain in thexandydirections,respectively.Nis the number of grid points in both theiandjdirections.The DIS-RAND is based on the randomly distributed Cartesian grid and defined by

Table 6 CPU times and L2 errors on STRETCHED
First of all,on the ALT-RAND grid,the numerical solutions of WENO-JS,WENO-NM,and WENO-Nare shown in Fig.5,and the CPU times andL2errors are listed in Table 5.The WENO-JS generates significant numerical oscillations.Both WENO-NM and WENO-N can obtain very smooth and symmetrical results,however the CPU time of WENO-NM is much smaller than that of WENO-N.
Secondly,on the STRETCHED grid,the results of WENO-JS,WENO-NM,and WENO-N are shown in Fig.6 and the CPU times andL2errors are listed in Table 6.All of the three schemes can predict smooth results,however,it is obvious that the result of WENO-JS is a little asymmetrical.TheL2error of WENO-NM is smaller than WENO-JS without consuming too much CPU time.

Fig.6 Density contour on STRETCHED grid at t=10 s.30 equally spaced contour lines from 0.55 to 0.95.a WENO-JS,b WENO-NM,c WENO-N
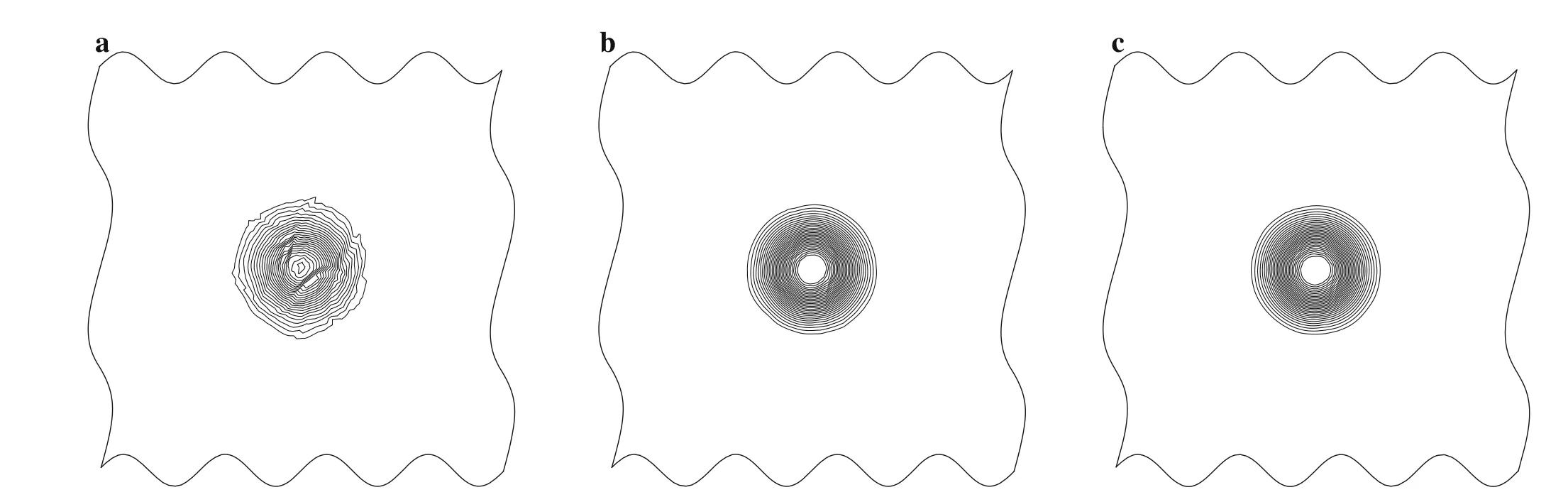
Fig.7 Density contouron DIS-RANDgrid at t=10 s.30 equally spaced contour lines from 0.55 to 0.95.a WENO-JS,b WENO-NM,c WENO-N

Table 7 CPU times and L2 errors on DIS-RAND

Fig.8 Non-uniform grid used for the 2D shock–vortex interaction
Thirdly,on the DIS-RAND grid,the numerical solutions of WENO-JS,WENO-NM,and WENO-N are plotted in Fig.7.The numerical result of WENO-JS is significantly deteriorated(Fig.7a),but WENO-NM and WENO-N can both predict very good results(Fig.7b,c).However,WENO-NM is more efficient than WENO-N according to Table 7.
In summary,this numerical test case shows that WENONM is a better choice on non-uniform and curvilinear grids.
3.4 Isentropic vortex and weak shock wave interaction
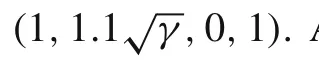

Fig.9 Density contours for the 2Dshock-vortex interaction at t=0.2 s.50 contours from 0.895 to 1.195.a Reference,b WENO-JS,c WENO-NM

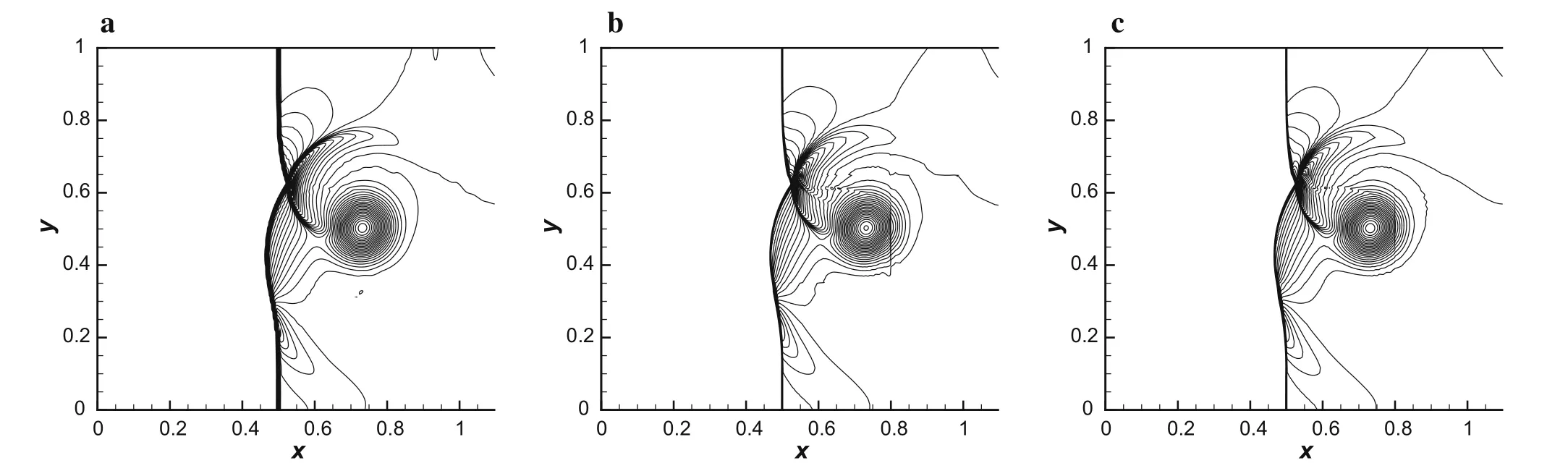
Fig.10 Density contours for the 2D shock–vortex interaction at t=0.4 s.50 contours from 1.005 to 1.305.a Reference,b WENO-JS,c WENO-NM

Fig.11 Density contours for the 2D shock–vortex interaction at t=0.6 s.50 contours from 1.005 to 1.235.a Reference,b WENO-JS,c WENO-NM
The grid used in this testis shown in Fig.8.The number of grid pointsis401 in thei-direction and 201 in thej-direction.The refined region in thei-direction is[0.45,0.8]with 269 grid points and in thej-direction is[0.35,0.65]with 153 grid points.The top and bottom boundaries are slip walls.The numerical solution obtained by the WENO-JS scheme on an 801×401 uniform grid is considered to bethereference solution.
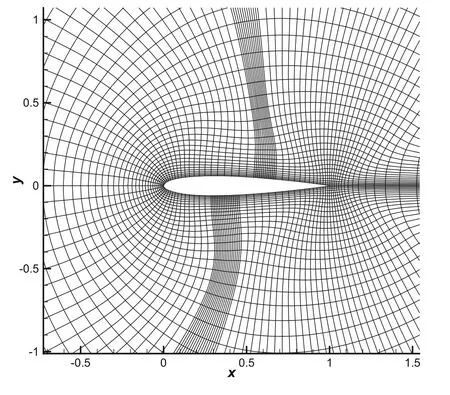
Fig.12 Structured grid used for computing transonic flow past an NACA0012 airfoil
The density contours computed by WENO-JS scheme and WENO-NM scheme att=0.2,0.4,0.6 s are shown in Figs.9–11,respectively.It can be seen that both of the schemes can capture the shock waves clearly and sharply.In Fig.9,the result of WENO-NM is smoother and is closer to the reference solution than that of WENO-JS.In Fig.10,there is a spurious structure predicted by WENO-JS which is not shown in the result of WENO-NM.Finally,in Fig.11,this structure becomes stronger for the WENO-JS and is much weaker for WENO-NM.

Fig.13 Distributions of surface pressure coefficient
3.5 Subsonic flow around NACA0012 airfoil
Transonic steady flow around an NACA0012 airfoil is simulated to demonstrate the performance of the WENO-NM scheme on non-uniform curvilineargrids.The Mach number used in the simulation is 0.8,and the angle of attack is 1.25◦.Figure 12 shows the grid used in the simulation.The grid number is 181×61,the upper and lower surface each have 61 points.We directly refine the grid near the shock wave region without changing the distribution in other places.The Courant number is 1.0 and the computations are started with uniform flow.The contour of pressure is shown in Fig.14.It is observed that WENO-NM can obtain smooth result on the non-uniform curvilinear grid.Pressure coefficient distributions are plotted in Fig.13.The result of the WENO-NM scheme is closer to the “exact”solution than that of the WENO-JS scheme.Here,the “exact”solution refers to the numerical result predicted by WENO-JS on a 361×61 nearuniform grid.
4 Conclusions
In the present paper,a modified WENO scheme called WENO-NM has been derived to compute compressible flows on non-uniform grids.This modification reformulates the fifth-order WENO-JS scheme designed on uniform grids in terms of one cell-averaged value and its left and/or right interfacial values of dependent variables.The WENO-NM scheme reduces numerical errors and can obtain smooth results when the scheme is applied on non-uniform grids,and will revert to the original WENO-JS scheme on uniform grids.This kind of modification is very flexible and can be applied to other optimized WENO schemes and WENO-like schemes.Several test cases are solved numeri-cally to study the performance of the proposed scheme.The numerical results show that the WENO-NM scheme can predict smoother and more accurate results than the WENO-JS scheme.

Fig.14 Pressure contour around NACA0012 airfoil.a WENO-JS,b WENO-NM
AcknowledgementsThe project was supported by the National Natural Science Foundation of China(Grant 11672160)and the National Key Research and Development Program of China(Grant 2016YF A0401200).
1.Tam,C.K.W.,Webb,J.C.:Dispersion-relation-preserving finite difference schemes for computational acoustics.J.Comput.Phys.107,262–281(1993)
2.Lele,S.K.:Compact finite difference schemes with spectral-like resolution.J.Comput.Phys.103,16–42(1992)
3.Shen,M.Y.,Zhang,Z.B.,Niu,X.L.:A new way for constructing high accuracy shock-capturing generalized compact difference schemes.Comput.Methods Appl.Mech.Eng.192,2703–2725(2003)
4.Zhou,Q.,Yao,Z.H.,He,F.,et al.:A new family of high-order compact upwind difference schemes with good spectral resolution.J.Comput.Phys.227,1306–1339(2007)
5.Sun,Z.S.,Ren,Y.X.,Zha,B.L.,et al.:High order boundary conditions for high order finite difference schemes on curvilinear coordinates solving compressible flows.J.Sci.Comput.65,790–820(2015)
6.Deng,X.G.,Mao,M.L.,Tu,G.H.,et al.:Geometric conservation law and applications to high-order finite difference schemes with stationary grids.J.Comput.Phys.230,1100–1115(2011)
7.Gamet,L.,Ducros,F.,Nicoud,F.,et al.:Compact finite difference schemes on non-uniform meshes.Application to direct numerical simulations of compressible flows.Int.J.Numer.Methods Fluids 29,159–191(1999)
8.Zhong,X.L.,Tatineni,M.:High-order non-uniform grid schemes for numerical simulation of hypersonic boundary-layer stability and transition.J.Comput.Phys.190,419–458(2003)
9.Shukla,R.K.,Zhong,X.L.:Derivation of high-order compact finite difference schemes for non-uniform grid using polynomial interpolation.J.Comput.Phys.204,404–429(2005)
10.Shukla,R.K.,Tatineni,M.,Zhong,X.L.:Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier–Stokesequations.J.Comput.Phys.224,1064–1094(2007)
11.Cheong,C.L.,Lee,S.:Grid-optimized dispersion-relation preserving schemes on general geometries for computational aeroacoustics.J.Comput.Phys.174,248–276(2001)
12.Pereira,J.M.C.,Kobayashi,M.H.,Pereira,J.C.F.:A fourth-order accurate finite volume compact method for the incompressible Navier–Stokes solutions.J.Comput.Phys.167,217–243(2001)
13.Piller,M.,Stalio,E.:Finite-volume compact schemeson staggered grids.J.Comput.Phys.197,299–340(2004)
14.Lacor,C.,Smirnov,S.,Baelmans,M.:A finite volume formulation of compact central schemes on arbitrary structured grids.J.Comput.Phys.198,535–566(2004)
15.Fosso,A.,Deniau,H.,Sicot,F.,et al.:Curvilinear finite-volume schemes using high-order compact interpolation.J.Comput.Phys.229,5090–5122(2010)
16.Harten,A.,Engquist,B.,Osher,S.,et al.:Uniformly high order accurate essentially non-oscillatory schemes,iii.J.Comput.Phys.71,231–303(1987)
17.Wang,Q.J.,Ren,Y.X.:An accurate and robust finite volume scheme based on the spline interpolation for solving the euler and Navier–Stokes equations on non-uniform curvilinear grids.J.Comput.Phys.284,648–667(2015)
18.Liu,X.D.,Osher,S.,Chan,T.:Weighted essentially non-oscillatory schemes.J.Comput.Phys.115,200–212(1994)
19.Jiang,G.S.,Shu,C.W.:Efficient implementation of weighted ENO schemes.J.Comput.Phys.126,202–228(1995)
20.Wang,R.,Feng,H.,Spiteri,R.J.:Observations on the fifth-order weno method with non-uniform meshes.Appl.Math.Comput.196,433–447(2008)
21.Capdeville,G.:A central weno scheme for solving hyperbolic conservation laws on non-uniform meshes.J.Comput.Phys.227,2977–3014(2008)
22.Smit,J.,van Sint Annaland,M.,Kuipers,J.A.M.:Grid adaptation with weno schemes for nonuniform grids to solve convection dominated partial differential equations.Chem.Eng.Sci.60,2609–2619(2005)
23.Crnjari-Žic,N.,Maei,S.,Crnkovi,B.:Efficient implementation of WENO schemes to nonuniform meshes.Annali dell Universit di Ferrara 53,199–215(2007)
24.Cravero,I.,Semplice,M.:On the accuracy ofWENOand CWENO reconstructions of third order on nonuniform meshes.J.Sci.Comput.67,1219–1246(2016)
25.Martłn,M.P.,Taylor,E.M.,Wu,M.W.,et al.:A bandwidth optimized WENO scheme for the effective direct numerical simulation of compressible turbulence.J.Comput.Phys.220,270–289(2006)
26.Borges,B.,Carmona,M.,Costa,B.,et al.:An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws.J.Comput.Phys.227,3191–3211(2008)
27.Sun,Z.S.,Ren,Y.X.,Larricq,C.,et al.:A class of finite difference schemes with low dispersion and controllable dissipation fordnsof compressible turbulence.J.Comput.Phys.230,4616–4635(2011)
28.Wang,Q.J.,Ren,Y.X.,Sun,Z.S.,et al.:Low dispersion finite volume scheme based on reconstruction with minimized dispersion and controllable dissipation.Sci.China Phys.Mech.Astron.56,423–431(2013)
29.Zhu,J.,Qiu,J.X.:Anewfifth orderfinite difference WENOscheme for solving hyperbolic conservation laws.J.Comput.Phys.318,110–121(2016)
30.Guo,Y.,Xiong,T.,Shi,Y.F.:A positivity preserving high order finite volume compact-WENO scheme for compressible Euler equations.J.Comput.Phys.274,505–523(2014)
31.Fu,L.,Hu,X.Y.,Adams,N.A.:A family of high-order targeted ENO schemes for compressible- fluid simulations.J.Comput.Phys.305,333–359(2016)
32.Zhang,L.P.,Liu,W.,He,L.X.,et al.:A class of hybrid DG/FV methods for conservation laws ii:two-dimensional cases.J.Comput.Phys.231,1104–1120(2012)
- Acta Mechanica Sinica的其它文章
- Motion of the moonlet in the binary system 243 Ida
- Adaptive ANCF method and its application in planar flexible cables
- Analytical modeling and simulation of porous electrodes:Li-ion distribution and diffusion-induced stress
- Macro and micro mechanics behavior of granite after heat treatment by cluster model in particle flow code
- Effect of a viscoelastic target on the impact response of a flat-nosed projectile
- Highly accurate symplectic element based on two variational principles

