The influence of sub-grid scale motions on particle collision in homogeneous isotropic turbulence

Yan Xiong·Jing Li·Zhaohui Liu·Chuguang Zheng

List of symbols

DPM Discrete particle model

FDNS Filtered direct numerical simulation

HIT Homogeneous isotropic turbulence

LES Large eddy simulation

PDF Probability density function

RDF(g) Radial distribution function(dimensionless)

SGS Sub-grid scale

SPS Satellite particle simulation

LLength of the simulation domain

NcellNumber of cells in the simulation field

NpNumber of particles

dDiameter of particle

RSeparation distance of particle pair at collision radius

rSeparation distance of particle pair

VfieldVolume of the domain

VsVolume of the annulus with radiusr

StkParticle Stokes number based on the Kolmogorov scale

Sij,pStrain tensor rate of the flow at particle location

Rij,pRotation tensorrate of the flow at particle location

r.m.s. Root mean square

wrRadial relative velocity(dimensionless)

wr−Radial relative velocity in inward direction

βParticle collision kernel

τpParticle relaxation time

τkKolmogorov time scale of turbulence

TEEulerian integral time scale of turbulence

ηKolmogorov length scale of turbulence

νkKolmogorov velocity of the turbulence

1 Introduction

Inertial particles suspended in turbulent flow is important to a wide variety of atmospheric processes(pollutant transport,cloud or rain droplet formation[1],the formation of protoplanetary disks[2])and major industrial problems(engine spay,particle suspension in circulating fluidized beds[3],and turbulent mixing in combustion).Results of numerous simulations in this field[4]have shown that a broad range of aerosol particles tends to accumulate outside of vortices,in the high-strain regions of the flow.Such phenomenon is vital to particle settling[5,6],condensation[7],and inter-particle collisions.

Particle collision rate deeply affects the efficiency and security in these processes and has been extensively discussed in previous literatures[10–16].In their pioneer works on geometric collision rates,later known as the collision kernel,it is shown that the contribution from the particle relative velocity,termed as the turbulent transport effect,is most important whenτpis of the order ofTE.Whereas,the preferential concentration was found to follow a Kolmogorov scaling,it means that the so-called accumulation effect is evident atτp/τk≈ 1.Those illustrations were confirmed by both direct numerical simulation(DNS)and experiment[17].Moreover,with the assistance of DNS,the effect of particle inertia on the collision statistics,in the context of predicting the collision kernel,was discussed[13,18,19].Recently,it has also been found that the formation of the so-called caustic[20–23],which means multi-valued velocities in the limit of zero particle pair separation,notably enhances the collision rate.DNS has proven to be efficient for analyzing the behavior of collision statistics at small separations.However,it inevitably suffers from the well known computational limitation on the Reynolds numbers that can be achieved.This drawback of DNS motivates the development of largeeddy simulation(LES)in particle-laden flow.

LES provides a promising tool to address the turbulent flow in a more subtle way and has already been applied to particle-laden flow with some successes.In the framework of LES,only large scales are explicitly resolved,while the small scales are modeled to account for the“sub-grid scale”(SGS)stresses.Many works have reported that with the help of LES and a discrete particle model(LES-DPM),some fundamental issues about the particle-laden flow like the interaction between the coherent structures and the particle dispersion[8]can be addressed,and it can also be beneficial to investigate the complicated behavior such as the particle-laden opposed jet flow[9]or granular clustering phenomenon in the gas–solid riser[10].However,the absence ofSGS motion causes non-monotonic discrepancy on the variables,such as the radial distribution function(RDF)g(R)and radial relative velocities 〈|wr|〉,as a function of the particle Stokes number(Stk),as reported by Wang and Squires[11],Fede and Simonin[12],Pozorski and Apte[13],Jin et al.[14],Voßkuhle et al.[15],and Ray and Collins[16].It raises a huge challenge on how to predict these values correctly in LES[17].Besides,apart from the monodisperse particles issue mentioned above,Chen and Jin[18]give a systematic study on the effects of the absence of SGS motions on the bidisperse inertial particle collision process.They found the influence of the SGS motions on the particle pair dynamics is relatively smaller in the bidisperse case;however,an appropriate particle SGS model is still needed.

From previous studies, we knowclearly that turbulent collision of inertial particles is a small-scale process. The filtered SGS flow field in LES will play an important part in collision related variables like RDF, especially for particles with smallStk.And meanwhile,since particle collision is a two-or even a multiple-particle process the classical one-point model framework could hardly work on it;both the classic dynamic SGS model and other models for Lagrangian particle simulation in an LES framework could not recover the information needed for binary process statistics such as particle collision and concentration.Forexample,Pozorskiand Apte[13]implemented a Langevin-type formulation to reconstruct the SGS velocity in order to complement the particle velocity in SGS.The stochastic Langevin model proposed for SGS particle dispersion is a one-point model by construction,which exhibited excellent agreements when applied to reproduce the particle turbulent kinetic energy and the integral time scale seen by particles,asexpected.However,it failed to capture the RDF and other two-particle quantities.A structural approach,which mimics the important structural features of the SGS motion,should be conceived.Extensions of the model,by replacing the SGS velocity with a corresponding value seen by the particles,have been developed by Fede et al.[19],Berrouk et al.[20],Shotorban and Mashayek[21],Jin et al.[14],Pozorski and Apte[13],Bini and Jones[22],and Jin and He[23];however,these studies were unable to recover the physics accurately.Besides the Lagrangian stochastic method,some attempts have been made towards accounting for the SGS motion using the approximation deconvolution method(ADM),i.e.Refs.[24,25].Nevertheless,with insight of the method,the de-filtering procedure lacks a reasonable physical explanation and could hardly work for coarse LES or a higher Reynolds configuration.Very recently,a similar extension of ADM implementing a differential filter(DF)[26]exhibited improvement in predicting particle preferential concentration.However,currently,both ADM and similar models that aim at reconstructing the velocity field at scales beyond the filter size are not broadly adopted in this field yet and are still in need of further validation.

Obviously,a binary or even multi-particle process skeleton is needed for reasonable model construction in the LES framework for the particle pairdynamics.Astochastic model based on the two-point probability density function(PDF)transport equation was developed by Leonid et al.[27–29]for the joint PDF of particle pair separationrand their relative velocitywr.They closed the set of governing continuum equations with the help of the Lagrangian velocity structure function of inertia particles,and the model held over the whole range of Stokes number and gave reasonable predictions for the velocity correlations as well as the RDF.However,this model assumes that the correlation of fluid relative velocities along inertia particle pair trajectories is the same as the fluid-pair,which is only valid forS tk～1.Similarly,Chun et al.[30]used the perturbation expansions of particle pair separations and their relative velocities to close the drift term and diffusion term of the two-point PDF equation in the phase space,respectively,which is based on the locally linear flow assumption that works for small particles.In contrast to those,Rani et al.[31]recently considered the pair PDF as a Fokker-Planck form for comparably largeinertia particles and gaveaclosure to the diffusion tensor term with the help of the Eulerian fluidvelocity correlations at corresponding pair separations r.Nevertheless,currently,there is still no better model for particulate systems that can accurately account for particle pair dynamics of arbitrary-inertia particles.With the help of the theory mentioned above,in the LES framework,Ray and Collins[32]firstly attempted to achieve the pair dynamics of a sub-Kolmogorov inertial particle with so-called satellite particle simulation(SPS),in which the relative PDF transport equation in a higher-dimensional phase space is solved by Lagrangian particle simulation within SGS.The method exhibits the ability to capture the clustering and relative velocity statistics of inertial particles with particleStk≤0.4 correctly,and is also a promising platform to develop and validate the two-point models in LES.Besides,current development of the Lagrangian subgrid model(LSGS)[33]for predicting two-or multi-particle dispersions in Lagrangian turbulence exhibits its potential to recover the particle structure information in SGS,but more validation for inertia particles is still needed.The turbulent temporal and space correlation described in this model is the key to capture the particle pair dispersions.More related improvement regarding the space-time correlation in LES can be found in Refs.[34–37].

In this paper,we investigate the effects of filtering on RDF and other particle pair statistics across a wide range ofStkandr/ηas a function of filter scales,which roughly span the inertia and dissipation range in homogeneous isotropic turbulence(HIT).By comparing the corresponding results in FDNS and DNS,we can figure out the underlying relations betweeng(r)andwr,and also their dependence on SGS fluid.Furthermore,the scale shift mechanism caused by the filtering of SGS motions in LES is validated posteriorly,with the expectation to provide more insights into the particle pair dynamic interactions with SGS flow fields.

This paper is organized as follows.In Sect.2,we describe the details of the numerical methods employed to evolve turbulent flow and track inertial particles with collisions.Section 3 presents the results and discussions on the effects of SGS motions on inertial particle pair statistics such as clustering,relative velocity and collision kernels.In Sect.4,some concluding remarks are presented.

2 Numerical method

2.1 Fluid phase(DNS and FDNS)

The dimensionless governing equations for the fluid field shown below is solved on a cubical uniform mesh with 2563grid points,with the side length of the cubeLequal to 2π:

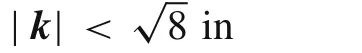
A filtered DNS field can be obtained by applying a cutoff filter in spectral space with various filter scales,which truncates the Fourier coefficients larger than the cutoff wavenumber(kc)in the turbulent energy spectra,

In this study,we choose the spectral filters withkc=8,16,21,32(for the case ofkc= 8,the filter width in the physical spaceΔis 16 times the original grid size,which means the residual part of the flow structure is severely destroyed and beyond the scope of LES applicability);the filter scales chosen coarsely cover the range of the inertial sub-zone which is always resolved in LES.The parameters of the filtered velocity field in Table 1 are computed using the standard definitions withkmaxreplaced bykc.

Table 1 Parameters and basic statistics in the simulations(dimensionless)

Fig.1 Energy spectrum of the DNS and the cut-off wavenumber of FDNS field with different filters.From left to right,the corresponding dashed lines mean kcη=0.1104,0.2207,0.2897,0.4415,respectively

Figure 1 exhibits the energy spectrum of the simulated flows in the DNS case with 2563grids,the inertial range is obvious displayed here,which is the essential requirement for the SGS analysis.Meanwhile,various normalized filter scales are labeled in Fig.1,which is attached to three FDNS cases to be discussed.It’s clearly shown that these scales roughly span the inertial and viscous sub-zone of turbulentkinetic energy(TKE)spectra,in which the small-scale motions are known as isotropic and homogeneous,so the model framework here is relatively feasible compared to the one at a large scale.

2.2 Discrete particle motion

In this paper,the dispersed phase is assumed to be dilute such that the one-way momentum coupling is adequate,and here,we could focus on the impacts of turbulence on the statistics of the dispersed phase.The density of particles is assumed to be much greater than that of the continuous carrier phase withρp/ρf≫ 1,and the diameter of particlesdis assumed not to exceed the Kolmogorov spatial microscaleηwith a constant valued=0.5ηin this paper.In this case,the equation of the particle’s motion can be written in the point-force approximation form with only the drag force working on the particle’s center of mass.Since the fluid density is much smaller than the particle,it is safe to disregard the forces arising from non-steady or inhomogeneity of the motion,like forces due to the acceleration or deceleration of the fluid(the virtual mass effect)and the Basset force which is attributed to the memory effect.Moreover,the primary objective of this paper is to study particle inertial effects on collision statistics,so the effect of an external body force is neglected as well.Therefore,the behavior of particles in turbulence is controlled only by the force of hydrodynamic resistance.Under these assumptions,the motion of a single heavy particle can be described with the equations below,which are solved by the implementation ofthe algorithm with fourth-order accuracy in space and second-order accuracy in time:

wherexpiandupiare the instantaneous position and velocity of the particle,ugi,pis the instantaneous fluid velocity at the particle location,andτpis the characteristic time of dynamic relaxation for the particles:

The particle drag coefficient(CD)and the particle Reynolds number(Rep)are expressed by

Meanwhile,the particle Stokes number(Stk)is defined as

in whichτkis the Kolmogorov timescale.

When the velocity field reaches a stationary state,particles are released with random distribution in the computational domain.All the simulations in the present study contain 1,200,000 particles in the flow.The initial velocity of the particle is set to be equal to the fluid velocity at the same location.Here,the fluid point velocity is computed via the accurate and well-tested partial Hermite interpolation scheme developed by Balachandar and Maxey[39].The statistics are calculated after a stationary condition is achieved,which is sustained for about six eddy turnovers.

2.3 Particle collision detection algorithm

The particle collision detection algorithm adopted here is analogous to the cell index method by Sundaram and Collins[40]with the optimization in the cell list and the range for detection.The total computation of collision detection per step isNp(27Np/Ncell−1)/2 compared toNp(Np−1)/2 of the initial one.Then,we can calculate the collision kernel by:

wherenis the number density in this field.Also,we can give our estimated result with the formula below

Here,g(R)is the RDF and 〈|wr|〉is the ensemble value of the modulus of particle pair radial relative velocities.They can be expressed by:

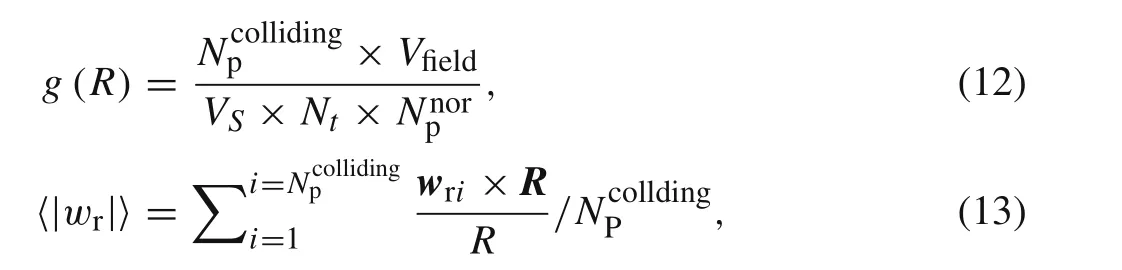
whereVfieldis the volume of the domain andVsis the volume of the annulus for detection,which isVs=4π[(R+δ/2)3−(R− δ/2)3],andNnorpis the number of particle pairs in the detection zone when particles are uniformly distributed.

3 Results and discussion

In this section,we present our results of numerical simulations with and without filtering.Firstly,two aspects regarding the particle collision process are discussed below,and then we combine these two effects to evaluate the influences of filtering on the collision kernel.

3.1 The influence of the absence of SGS motions on the particle preferential concentration

Firstly,we should get the results of the RDFg(r)with various St and particle pair distancesrof the DNS case in order to identify its underlying characteristics,and also set a benchmark for comparison.Figure 2 shows the variation ofg(r)as a function ofStkand particle separation distance within both DNS and FDNS as the background field.Here,we choose two types of particles withStk=0.5 and 3.0 to represent the small and relatively large-inertia particles,respectively.As to the case of FDNS,we choose the cutoff wavenumberkc=16.It is found that,regardless ofStk,theg(r)always decreases monotonically with separation distance for two differentStkin both DNS and FDNS,which means a power law formulation may lay behind.According to study by Reade and Collins[7],g(r)grows as a power law ofrwith the expression as g(r)=c0(S t)×(r/η)−c1(St)for a steady state,and this formula was confirmed for low-inertia particles.

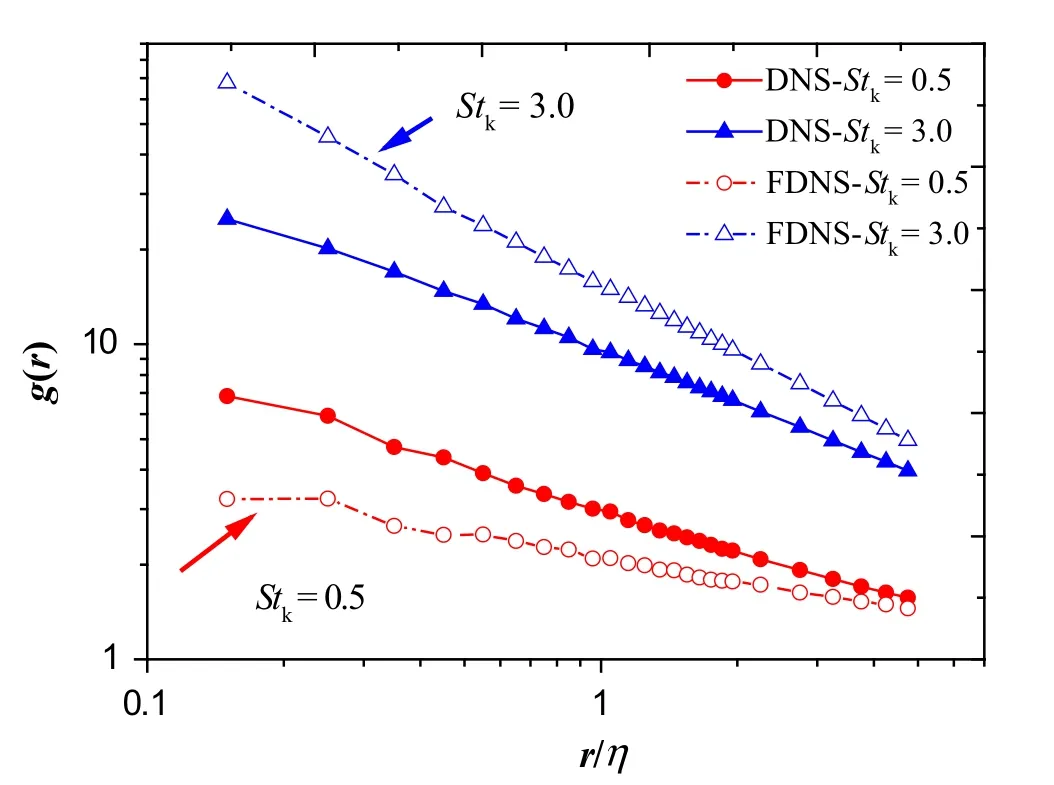
Fig.2 Variation of g(r)with and without filtering(kc=16)in terms of particle separation distance r/η two different Stokes numbers

DNS results obtained by Wang et al.[24]Maxey[41]have proved that the divergence of the particle velocity is positive in regions of high rotation and negative in regions of high strain rate,which implies that the phenomenon of particle clustering at the edge of the vortices is driven primarily by small-scale structures which centrifuge the inertial particles out of the cores of vortices.For the particles with large inertia,this small-scale effect is weak;however,for tiny particles which tend to follow the flow tracers,the particle trajectories have less chance to cross each other(so-called caustic),such that for intermediate particles,the clustering effect becomes most obvious,and this statement is consistent with Fig.3.

As stated above,the SGS structures play an important role in particle clustering.In Fig.2,we also focus on the influence of the absence of SGS vortices on particle preferential concentration,which is represented by the radial distribution functiong(r).It is evident that for particles withStk=0.5,g(r)decreases with the filtering process,whereas for larger particles,asStk=3.0,g(r)increases on the contrary,which indicates that the SGS structures work with different mechanisms for various inertial particles.This is clarified in Fig.3 in that the discrepancy ofg(r)is sensitive to theStkwhen filtered.For particles withStk＜1.5,the particle preferential concentration effect is a benefit from the centrifugal force of the SGS vortex,which leads to fewer chances to cluster after filtering;however,forStk＞1.5,SGS motions could hardly drive these particles anymore and they tend to homogenize the particle’s distribution,which results in a rise ing(r)with the absence of SGS motions.When theStkcontinually goes up to about8,the filter eventually has no influence,according to Fig..Similar results have been presented by Fede and Simonin],Jin et al.],and Chun et al.].Here,we verify similar trends at different separation distances rather than just the particle collision radius.

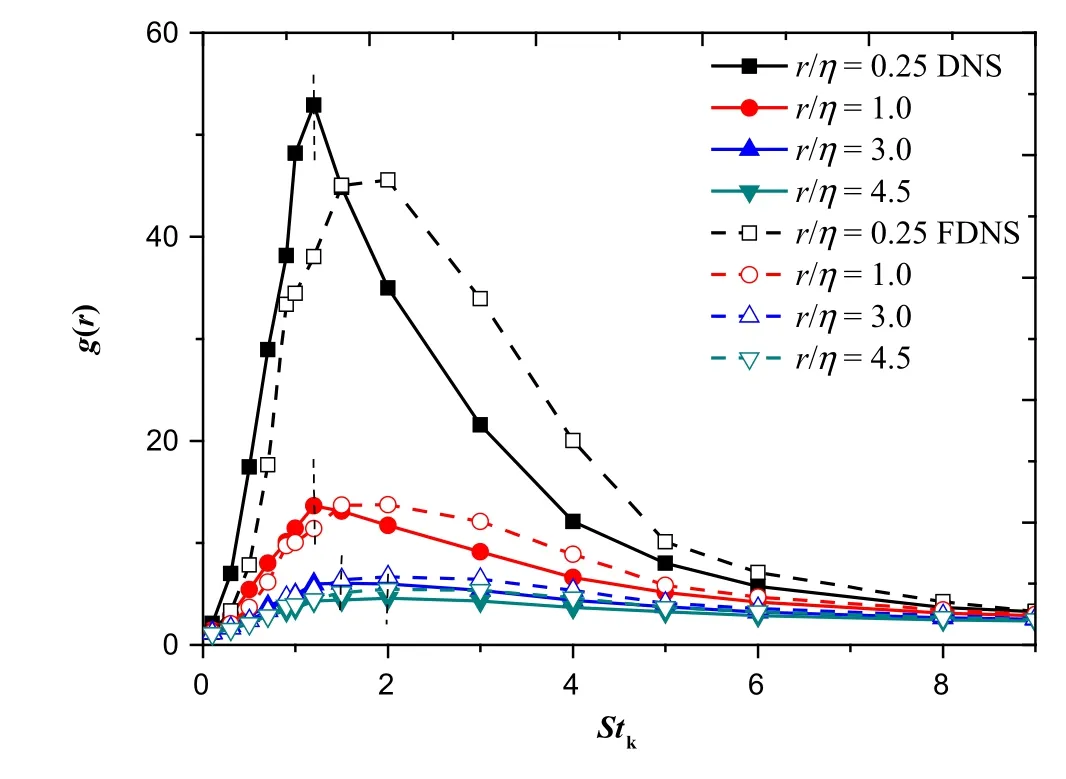
Fig.3 Radial distribution function g(r)along with Stk in FDNS with comparison to the results in DNS

Moreover,as previously reported,the location of the peak ofg(r)moves towards greaterStkwhen separation distance r increases,which is obviously presented in Fig.3.We may receive a hint that for a specific separation distancer,there always exists a corresponding class of particles with particular Stokes numbers that“resonate”at this point.For a largerr,the point with the strongest interaction effect shifts rightward,although the magnitude of the peak decreases as follows.It is known that in DNS,the resolved smallest vortex scale(Kolmogorov length scaleη)holds the strongest vortex intensity,which induces the particle clustering and then leads to a peak ofg(r)atStk≈1.Nevertheless,for filtered DNS flow,the smallest scale resolved is larger thanηDNSand that,in addition,leads to the requirement of a relatively largerτpto reach the “resonate”point.Afterwards,it turns out to be a scale shift towards larger particle inertia direction for a macro-scope,as can be found in Fig.3.Moreover,the key point here is that this scale shift results in the non-monotonic variance ofg(r)after filtering.

Figure 4 gives us an intuitive grasp of particle clustering with and without filtering.Here,we choose two types of inertial particles withStk=0.5 and 3.0 to represent the small and big particles,respectively,and the background vortex field is normalized by the r.m.s.value of the DNS case.This opposite behavior for different inertial particles just verifies the analysis above.

According to the procedure of filtering,the residual flow field is mainly controlled by the filter width,i.e.the cut-off wavenumberkcin this paper.It’s known thatkcis a determinative parameter in many SGS models,so is particle-laden flow.So,next,we are interested in the influence of the filter scale on the particle clustering effect.We choose three different filter widths here(cutoff wavenumberkc=32,21,16 with maxim wavenumberkmax=128)to roughly cover the whole range of the inertial sub-zone of the turbulent energy spectrum.Actually,in order to study the particles’collision rate later,we should pay more attention to the RDF of particles touching,which isg(r=R)(in whichRis the collision radius).

Figure 5a shows theg(r)in FDNS compared to the results of DNS under the three conditions mentioned above.It follows the trend ofg(r)in Fig.3 since this particular case is just for a specificg(r)atr=Rcollision.We can see clearly that the variance ofg(r)is strongly dependent on the filter width.Forkc=32,which means the flow structures are well retained in this field,the relative errors are small,especially for particles withStrmk≥2,for which the filtering process hardly has any impact ong(r).However,for smallkc＜32,such that the flow structures are severely destroyed,it really makes a difference.Apparently,the phenomenon of scale shift is the key that leads to the errors in FDNS.More details can be observed from Fig.5b,which gives us the relative errors at three different filter scales for the whole range of particles considered.Here,it’s clear that the discrepancy ofg(r)is a function of bothkcandStk.Obviously,as shown in Fig.5b,for particles withStkless than 1.5,the filtering process causes a sharp decrease forg(r)with a valley point as low as 50%ofStk=0.5.Oppositely,for particles with largerStk,theg(r)rises after filtering,which leads to a maximum error ofStk=4.0.Then,when the particle inertia continues increasing above about9,the ratio gradually approaches zero eventually.This trend was also reported by Jin et al.[14]and Ray and Collins[16]who analyzed it in a similar way as we do here.However,subtle changes and more details displayed here give us a chance to directly capture the location ofStkwith the maximum relative error and quantify the influence of filter width based onStk.

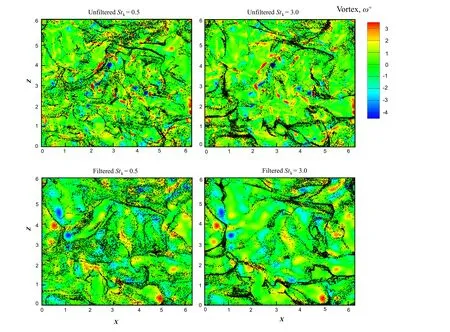
Fig.4 Slice of particle distribution with and without filtering;the background corresponds to vortices contours

Furthermore,according to the asymptotic analysis of the preferential concentration of particles with weak inertia by Maxey,we can treat the field of particle velocity with an Eulerian viewpoint and attach it to the local fluid strain rate tensorSijand vorticityRij.

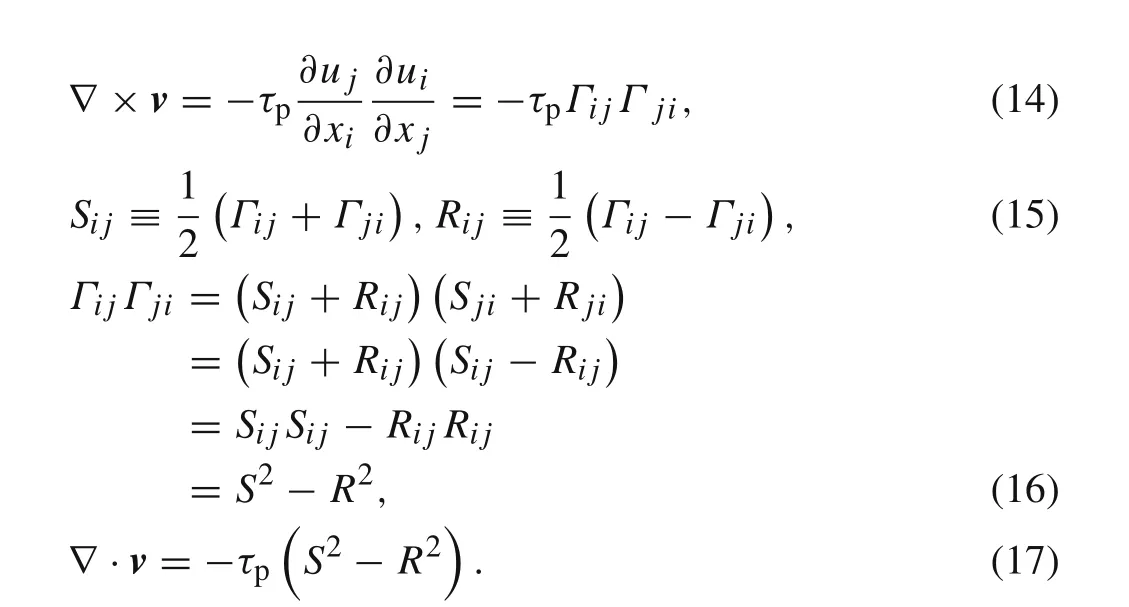
Here,S2andR2are the second invariant of the rate of strain and rotation tensors,respectively.In the weak-inertia limit,we can infer from Eq.(17)that when particles locate in the region of high vorticity,the negative value ofS2−R2leads to a positive value of the divergence of particle velocity which,in turn,throws the particle away.On the other hand,for particles in the region of high strain rate,the negative velocity divergence∇×vdecelerates the particles.Moreover,the balance process of these two mechanisms drives the particles to eventually accumulate in the area of high strain rate and low vorticity.However,for intermediate-inertia particles withStkaround 1,the bias between the particle path and fluid trajectory leads to the particles seeing a local fluid field apart from the fluid one.Hence,it’s better to replace the value ofS2−R2withSp2−Rp2in order to capture this process correctly,in whichSp2andRp2mean the corresponding flow field values seen by the particles,respectively.It’s observed from Fig.that the value ofSp2−Rp2increases with the Stokes number;it reaches its maximum atS tk≈0.5,and then decreases with a power law.It’s known that the peak ofg(r)locates atS tk≈1.0,as has been shown in Fig.5a.This deviation should be attributed to the prerequisite of the weak inertia limit in Eq.(17).As for inertia particles,the inertia effect and the local fluid structure should both contribute to the clustering effect,which pushes the peak towards a large inertia direction.

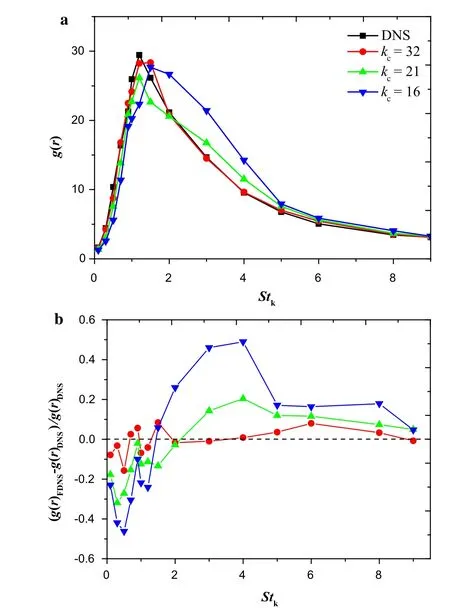
Fig.5 a Radial distribution function g(r= R)for particles get touched in DNS,FDNS(three different cutoff wavenumber kc).b Relative errors of g(r)in FDNS corresponding to the results in DNS for particles with different inertia

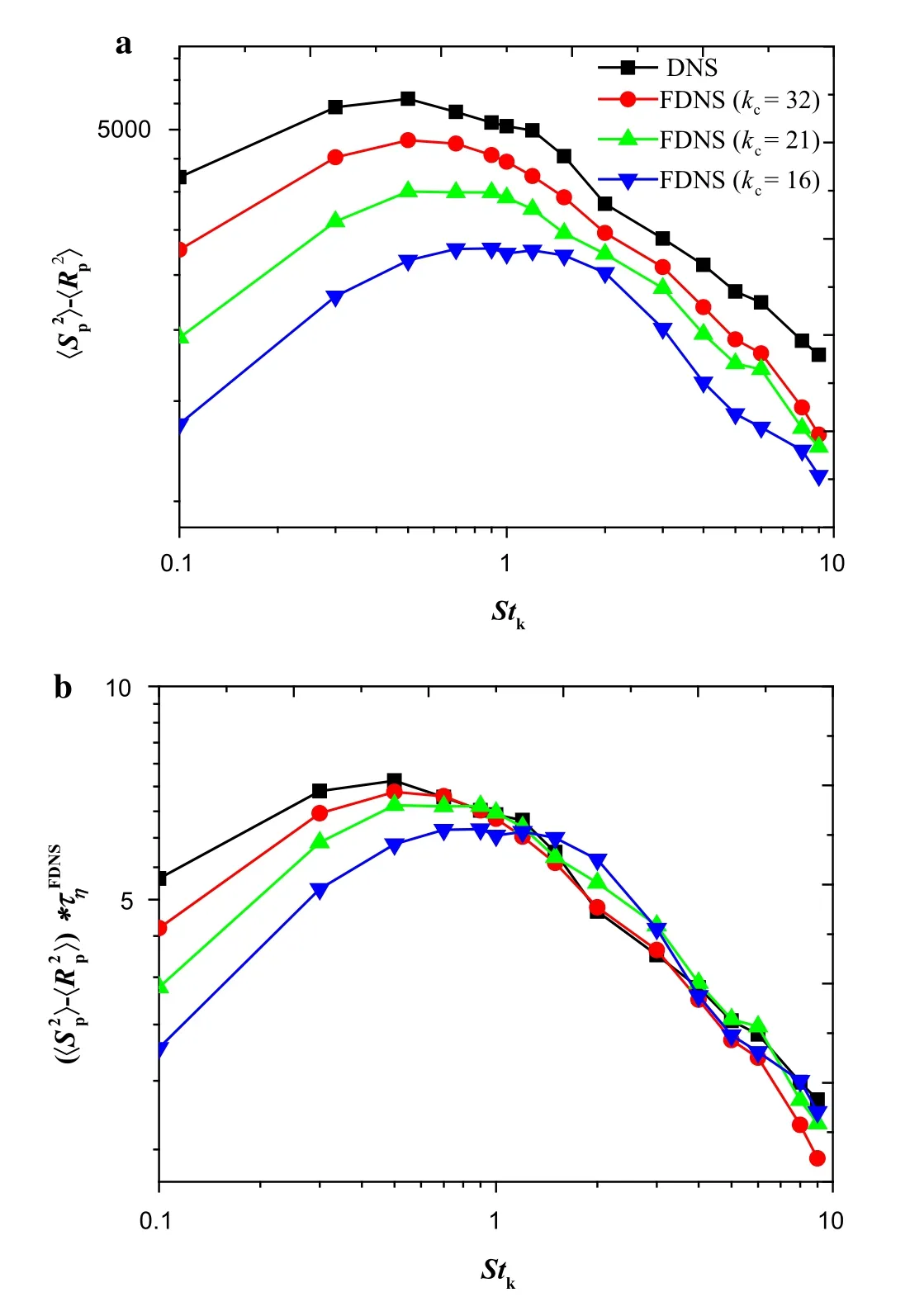
Fig.6 a Difference of the second invariant of the rate of strain and rotation tensors at the particle’s location with and without filtering.b Extensions by multiplying corresponding value with the resolved Kolmogorov time scale τηFDNS after filtering

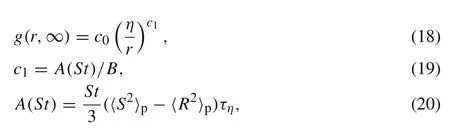
whereBin Eq.(19)denotes the dimensionless particle pair diffusion coefficient.As shown in Fig.6b,the peaks of these curves exhibit similar shifts towards a large inertial direction which is similar ing(r)as shown in Fig.5a.It’s really interesting that for small-inertia particles, the value decreases with filtering and then experiences an increase after it goes beyond the point of inflection atS tk≈1.5 which is identical tog(r).It inspires us that for intermediate-inertia particles withS tkaround 1,the particle clustering effect might be effectively predicted with the help of this local field variable contained in SGS model.

3.2 The influence of the absence of SGS motions on the radial relative velocity of particle pairs

In this section,we will discuss the other major component of the collision kernel for particles,i.e.the radial relative velocity(wr).Figure 7 shows the PDF ofwrwhich is normalized by its r.m.s value〈w2r〉1/2as a function of separation distance r with two particularStk,a0.5 andb3.0,respectively.It’s obvious that the PDF becomes broader asr/ηincreases.A similar trend was also observed by Bec et al.[25]and Salazar and Collins[42],in which several low-order moments ofwrwere discussed in detail.It can be explained that,with increasing the separation distance between the inertia particles,their velocities become increasingly uncorrelated,thus leading to broader PDFs until this effect will eventually saturate,whenr/ηis above about 4.Figure 7 also shows that for all the PDFs,the negative part is slightly larger than the positive one which leads to the asymmetry in the PDF,and that also results in the negative skewness.It’s noticeable that the largerwr−(negative radial relative velocity)also enhances the particle clustering effect,and the connection between them will be revealed later.Moreover,the PDF exhibits exponential tails which can be expressed with Eq.(21)by Wang et al.[24]

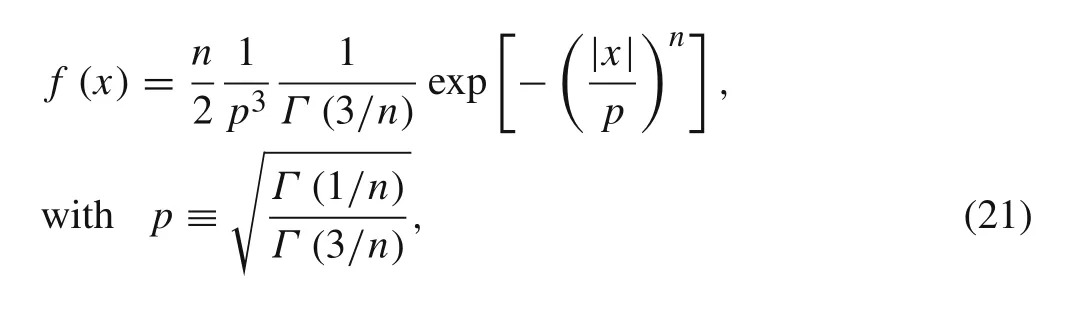
Fig.7 Variation of the PDF of radial relative velocity at the indicated values of Stokes number and at r/η of a 0.5 and b 3.0

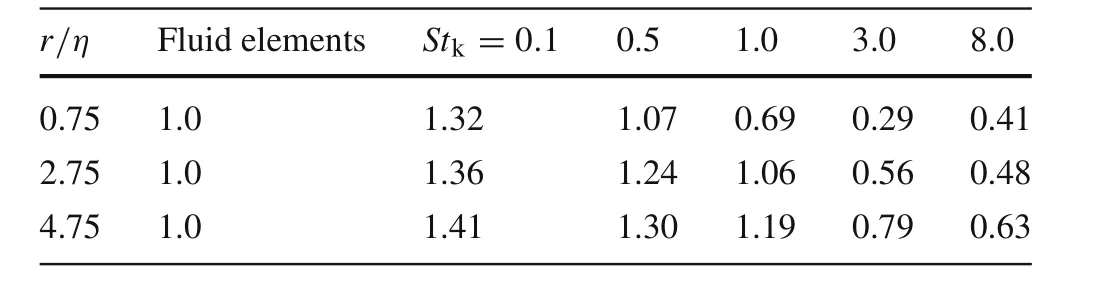
Table2 Exponential index n for different separation distances and particle inertias

whereΓis the gamma function.The PDF above has a unit standard deviation and itrepresents a standard Gaussian PDF forn=2,and a simple exponential one forn=1.As shown below(Table 2),the larger the particle inertia,the smaller the value ofn.It indicates that along with the increasing of particle inertia(in the range ofS tk～O(1)),the relative velocity is more intermittent,namely,the more probabilities of occurrences of extremely small or large values.However,for very large inertial particles,their behaviors in turbulence are assumed to be free molecule particles which leads to a Gaussian PDF and that is beyond our scope in this paper.

Figure 8 compares the filtered and unfiltered PDFs ofwrof two pair separations forStk=0.5 andStk=3.0 with three different filter widths used above.It’s notable that the filtered PDFs are strongly dependent on particlesStknumber.For tiny particles withStk=0.5(as shown in Fig.8a,c),the process of filtering makes the PDF broader for both separation distances considered.However,for larger particles(as shown in Fig.8b,d),the opposite trend is shown,i.e.the filtering process sharply narrows the PDF.Close inspection of Fig.b,d reveals that the filtered PDFs for larger particles converge into a single curve which differ from tiny particles withStk=0.5.It might hint that large particles withStk＞3 should be more sensitive to the integral scale in the flow in terms of particle radial relative velocity.When the flow structures in SGS are separated from the flow field,the remaining large scale flow structures become more prominent,and then large particles turn out to be increasingly correlated,which leads to a narrow PDF.But for tiny particles which are more likely to respond to SGS structures,the lack of such fluid motions might cause the neighbor particles to be less correlated and then spread the PDFs.These different effects of filtering in PDF indicate the similar trend ofg(r),and it might be more clear when we compare the higher moment of PDF,such as the skewnessS(r/η,Stk)= 〈w3r〉/〈w2r〉3/2to theg(r),which will be shown below.

Fig.8 Effect of filtering on the radial relative velocity PDF at:Stk=0.5 and r/η a 0.75 and c 4.75;and Stk=3.0 and r/η b 0.75 and d 4.75.Solid lines represent the DNS case,dashed lines cut-off wavenumber kc=32,dot lines kc=21,and dash-dot lines kc=16

Fig.9 Variation of the skewness of the PDF of the radial relative velocity as a function of r/η and particles Stk in DNS results as benchmark

Figure 9 shows the dependence ofS(r/η,St)on the particle pair separationsrat differentStkin DNS and FDNS.It has been firstly pointed out by Wang et al.[24]that particles with lowStkexhibit a higher negative skewness ofwrthan both the fluid tracers and the heavy particles.Here,we verify and expand this issue by considering the impact of separation distance[34].Also in Fig.9,the negative skewness means an inward center-in-line relative drift velocity of particle pairs which exists as a main contribution to particles clustering.For small particles withStk＜1,the absolute value ofSgoes higher asStkis increasing until it reaches its summit atStk=1,which is also the peak in RDFg(r).Afterwards,the absolute value ofSgoes down with the particle inertia increasing.We also observe the occurrence of the cross between different curves since the slope of each curve differs with particle inertia,and obviously two different regimes are demonstrated on that figure.For particles withStk＜1,the positive value of the slope rises up withStk,and then after its inflection point atStk=1,this value becomes negative and keeps going down for the remaining range of particles considered.Theoretically,Chun etal.[30]argued that low-St particle pairs undergo a balance process between net inward drift(i.e.〈wr〉p＜0)and outward diffusion flux which leads to equilibrium eventually.It’s clear that the small particles tend to accumulate in the region with high strain and low rotation ratesasStkincreases;however,this inward drift flux is gradually balanced by the diffusion process along with the increasing separation distancer/ηas a result of the positive slope.In contrast,when it comes to large particles for whichg(r)decrease withStk,the negative slope could lead to the strengthen of the inward drift and then results to an equilibrium state,such that〈wr〉p=0.Hence,this signature will be manifest in the odd-order moment such as the skewness presented here.

As we did in the PDFs ofwr,Fig.10a–c verifies the effect of filtering on the skewness at three specific values ofStkalong with ther/η.It’s notable that at lowStk,the skewness is reduced by filtering,but when it is highStk,an opposite trend is captured,and both the effects are reinforced with increasing the filter width monotonically.The results seem to be reasonable when compared to the variance ofg(r)in that the reduced negative skewness for particles within the range ofStk＜1 caused by filtering means a decrease inw−r,which leads to the lower particle concentration in the region with high strain and low vorticity,i.e.the smaller value ofg(r).In contrast,for larger particles withStk＞1,a higher negative skewness value is observed,which indicates that the preferential concentration is strengthened afterwards,and that is consistent with Fig.5.This opposite trend caused by filtering is similar tog(r),and this is well displayed in Fig.11.The curve of the skewness ofw(r)versusStkexhibits a“scale shift”towards large inertia after filtering from a macro-scope,and as can been clearly seen from Fig.11,the inflection point is also impacted by the particle pair separationr,for which the point moves right at larger separation.Recall the similar trends displayed in Fig.3,in that it can be inferred that the mechanism of scale shift ing(r)really works in the odd order moments ofw(r),and it also causes the errors in 〈|wr|〉indirectly.At this point,it might be instructive to look at the variation of 〈|wr|〉as a function of cut-off wavenumberkc,since this value is always used in some collision kernel models.

Fig.10 Variation of the skewness of the PDF of the radial relative velocity as a function of r/η and particles Stk in FDNS compared to the results in DNS.a–c Filtered DNS results with different filter scales at three specific St=0.1,1.0,3.0 respectively

The influence of filtering on the 〈|wr|〉shown in Fig.12a is consistent with the observation reported in Jin et al.[14].Unlike the appearance of the PDFs or the skewness discussed above,the filtered curve of 〈|wr|〉experiences a monotonic reduction as the filter width increases for all the particles’Stokes numbers.Close inspection of Fig.12b reveals that the variance of 〈|wr|〉exhibits non-monotonic dependence on theStk,and for a given filter width such askc=16,the maximum relative error could reach 35%that occurs atStk=4.0.The positive slope shown indicates that the small inertia particles are more sensitive to the filtered SGS motions and the error will go to zero as the particle inertia increasing eventually.Besides that,when we compare this trend with the curves in Fig.5b,it is interesting that these two physical processes seem to undergo a complementary mechanism for filtering,and that contributes to a balance process in the collision statistics for the largeStk,which will be discussed in the next section.

Based on the existing theories,the radial relative velocity for inertia particles is governed by the interaction of particles with both the large-scale energetic eddies and the small-scale dissipative eddies,i.e.the so-called acceleration mechanism and shear mechanism,respectively.In a previous study,Wang et al.[24]modified the model by Kruis and Kuster[43],which is under the assumption that the PDF ofwris Gaussian,with the form as

Fig.11 Effects of filtering on the skewness of wr versus particle inertia at separation r/η=1.0

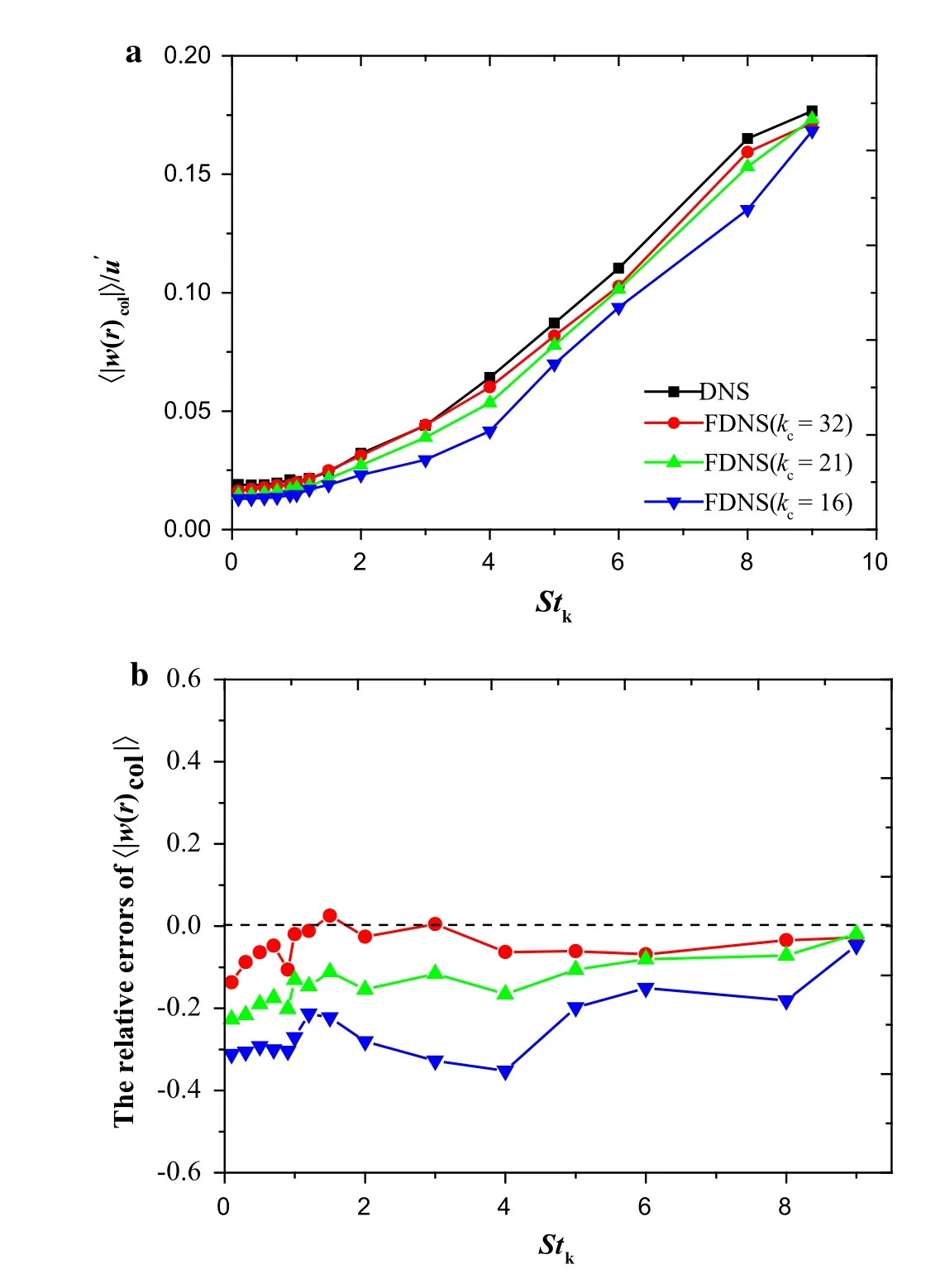
Fig.12 a Effect of filtering on the variation of absolute value of the radial relative velocity 〈|wr|〉with Stokes number which is normalized by the Kolmogorov velocity scale.b Exhibits the relative errors of〈|wr|〉in FDNS compared to the values in DNS with three different scales in the range of the inertia area are considered here

whereθ=1.8τp/TE,γ=0.183u′2/v2κ,τpis the particle residual time,T Eis the Eulerian integral time scale,vkis the Kolmogorov velocity,and the factorC wis set to be 1.7 to fit the numerical results in this paper.For particles with zero inertia,the local shear mechanism dominates the 〈|wr(R)|〉,and withθgoing to zero,Eq.(22)reduces to the Saffman and Turner’s expression as

Furthermore,in the FDNS flow field,the SGS eddies have been moved out,which leads to the fall in shear mechanism for small-inertia particles.However,for very large-inertia particles withS tk～O(10),the acceleration mechanism dominates and remains nearly unaffected within the filtered DNS,as shown in Ref.[14].As to intermediate-inertia particles,since the particle residual timeτphere is far from both the turbulent characteristic integral timescale and also the Kolmogorov timescale in this case,which makes it to be the most complicated one to predict.In Fig.13,we verify the model of Eqs.(22)–(24)in both DNS and FDNS.For the case of FDNS,we substitute the parameters in DNS such asTEandvkwith their corresponding values in FDNS.It can be seen that this model correctly predicts this value for small-inertia particles withS tk≤0.5 in both DNS and FDNS.As the inertia increases,the asymmetric nature of PDF related to the clustering effect will lead to the deviation of the model within the range ofS tk～O(1).However,for very large-inertia particles,the PDF is asymptotic Gaussian which is suitable for this model framework.It can be concluded that the biases of the model might mainly owe to the fact that the skewness of PDF in this area is negative,which does not satisfy the Gaussian precondition of this model.

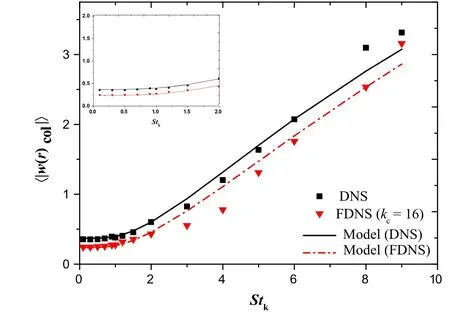
Fig.13 Performance of the model by Wang et al.[24]in both DNS and FDNS;for the case in FDNS,parameters in the model have been replaced by the characteristic values within the filtered flow

3.3 The combination effects of the absence of SGS motions on the particle collision kernel

In this section,collision statistics are carried out in detail both with and without filtering.As previously studied by Wang et al.[24]and Sundaram Collins[40],we use the concept of the collision kernel to analyze the collision rate in turbulence.The collision kernel is defined below

where the particle collision kernel is normalized by the collision kernel for fluid elementsβ0.The above formula gives us the estimate value of the collision kernel;however,it can also be directly calculated from collision statistics:

Fig.14 a Effects of SGS motions on the collision kernel versus the particle Stk number with respect to g(r)and 〈|wr|〉.The solid lines correspond to the results in DNS and the dash dot lines means the results from FDNS.b The relative errors of the value of the collision kernel in FDNS compared to the results in DNS as a function of filter width and particle Stk number

whereNcalTis the collision number of times per collision step and per unit volume andnis the particle number density.Also,Eq.(26)is valid for FDNS when the particle Stokes number based on turbulent Kolmogorov time scaleS tkis in the range ofO(0.1～10).

Since the effects of filtering on the RDFg(R)and the radial relative velocity are shown above,we can now explore their corresponding effects on the collision kernel.Figure 14a gives us a comprehensive scope that the cause of the discrepancy in FDNS strongly depends on the particle’s inertia.For small particles,the filtering process causes an obvious decrease in bothg(R)and 〈|wr|〉,which inevitably causes a sharp decline in the collision kernel.But for larger par-ticles withS tkabove 2,the upgoingg(R)will eliminate the influence of the drop in 〈|wr|〉which eventually comes to a stable consistent process between DNS and FDNS.Figure 14b exhibits the relative errors ofβin FDNS as a function of the filter width atvariousS tk.The absence of SGS fluid indeed causes an obvious fall inβfor small particles,with a maximum relative error as much as 60%atS tk=0.5.However,for particles withS tk≥3.0,the effect of filtering vanishes at all the filter widths considered,which is consistent with the observations of Jin et al.[14].In order to address the discrepancy at smallS tk,we must stress the importance of the accumulation effect in this range as it is clearly shown in Fig.14a thatg(R)dominates the contribution to the collision kernel in this area.Since,as previously studied,the preferential concentration is prominent atτp≈τk,the scale shift that occurs ing(R)within the filtered flow field would cause a sharp decrease for those small-inertia particles withS tk≤2.0 which leads to a decline in the collision kernel.Furthermore,it’s reasonable that the relative errors could be enlarged with a higherRλ.Since the ratio ofTE/τkwill amplify with the increasingRλ,the scale gap between the preferential concentration and the turbulent transport effect,which is dominant atτp≈TE,could be enlarged,and this highlights the influence ofg(R)in the collision kernel at smallS tk.It’s also reported[16]that the curve of the filtered collision kernel approaches the DNS one mor slowly than the observation in Ref.[14].According to the results in this paper,this can be attributed to the higherRλof the DNS field used in their simulation,which strengthens the particle accumulation.The dependency of the effects of filtering on the collision kernel on the Taylor micro-scale Reynolds numberin an LES framework should be considered in further research,since the modelling of the high Re flow is the key motivation for developing the LES-DPM method.particle collisions,the particle-laden isotropic turbulent flow field obtained by DNS is filtered using sharp cut-off filters in spectral space.Current results indicate that the absence of SGS motions in FDNS can significantly modify the particle collision statistics,including the RDF,radial relative velocity and collision kernel,and the following conclusions can be drawn:

(1)The effects of filtering process on the radial distribution functiong(r)of particles is strongly dependent on theStk.The“resonate”Stkof inertia particles increases in the filtered DNS field whereηfiltered＞η,which is responsible

4 Conclusions

SGS motions play an important role in the collision process of inertial particles suspended in turbulence.In this work,in order to investigate the influence of SGS motions on the for the scale shift and the non-monotonic discrepancy ofg(r)in FDNS.

(2)The absence of SGS motion leads to a monotonic decrease in the radial relative velocitywr.And the relationship between the particle clustering effect and the radial relative velocity at SGS has also been revealed,which is observed only in the high-order odd-order moment of probability density function(PDF)ofwr,i.e.skewnessS.The peak ofg(r)is found to correspond with the valley point of theS,which is always negative for inertia particles.Besides,similar to theg(r),the scale shift also occurs in the curve ofSdue to the filtering of SGS motion.

(3)Two main mechanisms,which contribute to the collision kernel of inertia particles,give totally different responses to the filtering process.Above all that,in FDNS,theg(r)andwrembody a complementary mechanism,i.e.theg(r)decreases along with theStk,whereas thewrexplores the opposite trend after filtering,which results in a consistent collision kernel with DNS forStk＞3.0.However,it’s evident that a more suitable collision kernel model with concern of structural information within the SGS is needed,especially for small particles withStk≤3.0.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grants 51390494,51306065,and 51276076),the Foundation of State Key Laboratory of Coal Combustion(Grant FSKLCCB1702).

1.Grabowski,W.W.,Wang,L.P.:Growth of cloud droplets in a turbulent environment.Annu.Rev.Fluid Mech.45,293–324(2013)

2.Liubin,P.,Paolo,P.:Turbulence-induced relative velocity of dust particles.IV.Collis Kernel.Astrophys.J.797,101(2014)

3.Senior,R.C.,Grace,J.R.:Integrated particle collision and turbulent diffusion model for dilute gas-solid suspensions.Powder Technol.96,48–78(1998)

4.Squires,K.D.,Eaton,J.K.:Preferential concentration of particles by turbulence.Phys.Fluids A Fluid Dyn.3,1169–1178(1991)

5.Wang,L.P.,Maxey,M.R.:Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence.J.Fluid Mech.256,27–68(1993)

6.Dejoan,A.,Monchaux,R.:Preferential concentration and settling of heavy particles in homogeneous turbulence.Phys.Fluids 25,013301–013316(2013)

7.Reade,W.C.,Collins,L.R.:Effect of preferential concentration on turbulent collision rates.Phys.Fluids 12,2530–2540(2000)

8.Luo,K.,Fan,J.,Jin,H.,et al.:LES of the turbulent coherent structures and particle dispersion in the gas-solid wake flows.Powder Technol.147,49–58(2004)

9.Sun,W.,Zhong,W.,Zhang,Y.:LES-DPM simulation of turbulent gas-particle flow on opposed round jets.PowderTechnol.270,302–311(2015)

10.Wang,T.,He,Y.,Yan,S.,et al.:Cluster granular temperature and rotational characteristic analysis of a binary mixture of particles in a gas-solid riser by mutative Smagorinsky constant SGS model.Powder Technol.286,73–83(2015)

11.Wang,Q.,Squires,K.D.:Large eddy simulation of particle laden turbulent channel flow.Phys.Fluids 8,1207–1223(1996)

12.Fede,P.,Simonin,O.:Numerical study of the subgrid fluid turbulence effects on the statistics of heavy colliding particles.Phys.Fluids 18,045103(2006)

13.Pozorski,J.,Apte,S.V.:Filtered particle tracking in isotropic turbulence and stochastic modeling of subgrid-scale dispersion.Int.J.Multiph.Flow 35,118–128(2009)

14.Jin,G.,He,G.-W.,Wang,L.-P.:Large-eddy simulation of turbulent collision of heavy particles in isotropic turbulence.Phys.Fluids22,055106(2010)

15.Voßkuhle,M.,Pumir,A.,Lévêque,E.,et al.:Prevalence of the sling effect for enhancing collision rates in turbulent suspensions.J.Fluid Mech.749,841–852(2014)

16.Ray,B.,Collins,L.R.:Preferential concentration and relative velocity statistics of inertial particles in Navier Stokes turbulence with and without filtering.J.Fluid Mech.680,488–510(2011)

17.Benyahia,S.,Sundaresan,S.:Do we need sub-grid scale corrections for both continuum and discrete gas-particle flow models?Powder Technol.220,2–6(2012)

18.Chen,J.,Jin,G.:Large-eddy simulation of turbulent preferential concentration and collision of bidisperse heavy particles in isotropic turbulence.Powder Technol.314,281–290(2017)

19.Fede,P.,Simonin,O.,Villedieu,P.,et al.:Stochastic modeling of the turbulent subgrid fluid velocity along inertial particle trajectories.In:Proceedings of the Summer Program,247–258.Stanford,USA(2006)

20.Berrouk,A.,Laurence,D.,Riley,J.,et al.:Stochastic Modeling of Fluid Velocity Seen by Heavy Particles for Two-Phase LES of Non-homogeneous and Anisotropic Turbulent Flows.Springer,Netherlands(2007)

21.Shotorban,B.,Mashayek,F.:A stochastic model for particle motion in large-eddy simulation.J.Turbul.7,N18(2006)

22.Bini,M.,Jones,W.P.:Large-eddy simulation of particle-laden turbulent flows.J.Fluid Mech.614,207–252(2008)

23.Jin,G.D.,He,G.W.:A nonlinear model for the subgrid timescale experienced by heavy particlesin large eddy simulation of isotropic turbulence with a stochastic differential equation.New J.Phys.15,035011(2013)

24.Wang,L.-P.,Wexler,A.S.,Zhou,Y.:Statistical mechanical description and modelling of turbulent collision of inertial particles.J.Fluid Mech.415,117–153(2000)

25.Bec,J.,Biferale,L.,Cencini,M.,et al.:Intermittency in the velocity distribution of heavy particles in turbulence.J.Fluid Mech.646,527–536(2010)

26.Park,G.I.,Bassenne,M.,Urzay,J.,et al.:A simple dynamic subgrid-scale model for LES of particle-laden turbulence.Phys.Rev.Fluids 2,044301(2017)

27.Leonid,I.Z.:Vladimir:statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications.New J.Phys.11,103018(2009)

28.Zaichik,L.I.,Alipchenkov,V.M.:Statistical models for predicting particle dispersion and preferential concentration in turbulent flows.Int.J.Heat Fluid Flow 26,416–430(2005)

29.Zaichik,L.I.,Alipchenkov,V.M.:Pair dispersion and preferential concentration of particles in isotropic turbulence.Phys.Fluids 15,1776–1787(2003)

30.Chun,J.,Koch,D.L.,Rani,S.L.,et al.:Clustering of aerosol particles in isotropic turbulence.J.Fluid Mech.536,219–251(2005)

31.Rani,S.L.,Dhariwal,R.,Koch,D.L.:A stochastic model for the relative motion of high Stokes number particles in isotropic turbulence.J.Fluid Mech.756,870–902(2014)

32.Ray,B.,Collins,L.R.:Investigation of sub-Kolmogorov inertial particle pair dynamics in turbulence using novel satellite particle simulations.J.Fluid Mech.720,192–211(2013)

33.Mazzitelli,I.M.,Fornarelli,F.,Lanotte,A.S.,et al.:Pair and multi-particle dispersion in numerical simulations of convective boundary layer turbulence.Phys.Fluids 26,055110(2014)

34.He,G.,Jin,G.,Yang,Y.:Space-time correlations and dynamic coupling in turbulent flows.Annu.Rev.Fluid Mech.49,51–70(2017)

35.Guo,L.,Li,D.,Zhang,X.,et al.:LES prediction of space-time correlations in turbulent shear flows.Acta Mech.Sin.28,993–998(2012)

36.Zhao,X.,He,G.-W.:Space-time correlations of fluctuating velocities in turbulent shear flows.Phys.Rev.E 79,046316(2009)

37.He,G.-W.,Wang,M.,Lele,S.K.:On the computation of space-time correlations by large-eddy simulation.Phys.Fluids 16,3859–3867(2004)

38.Eswaran,V.,Pope,S.B.:An examination of forcing in directnumerical simulations of turbulence.Comput.Fluids16,257–278(1988)

39.Balachandar,S.,Maxey,M.R.:Methods for evaluating fluid velocities in spectral simulations of turbulence.J.Comput.Phys.83,96–125(1989)

40.Sundaram,S.,Collins,L.R.:Collision statistics in an isotropic particle-laden turbulent suspension.Part 1.Direct numerical simulations.J.Fluid Mech.335,75–109(1997)

41.Maxey,M.R.:The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields.J.Fluid Mech.174,441–465(1987)

42.Salazar,J.P.L.C.,Collins,L.R.:Inertial particle relative velocity statistics in homogeneousisotropic turbulence.J.Fluid Mech.696,45–66(2012)

43.Kruis,F.E.,Kusters,K.A.:The collision rate of particles in turbulent flow.Chem.Eng.Commun.158,201–230(1997)