Effect of compressibility on the hypervelocity penetration
W.J.Song·X.W.Chen·P.Chen
1 Introduction
Works by Birkhoff et al.[1]and Hill et al.[2]suggested a hydrodynamic theory of penetration(HTP)during WWII by invoking the incompressible Bernoulli equation

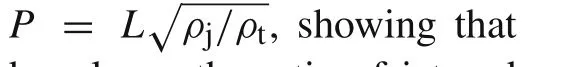
Basically,in the case of the ordnance velocity,the strengths of both the jet/rod and target play an important role in the penetration process.It is to be noted that Eichelberger[3]modified the incompressible Bernoulli equation to account for the strength effect when they analyzed the penetration by metallic jets

whereYjis the dynamic yield strength of the jet,Rtis the penetration resistance of the target,andpicis the pressure at the rod/target interface in the incompressible model with strength.
In other studies,Alekseevskii[4]and Tate[5,6]added two additional equations:the equation of motion of the nondeforming part of the rod and the relation between rod erosion rate and velocities when they analyzed the long rod penetration into metal/ceramic targets
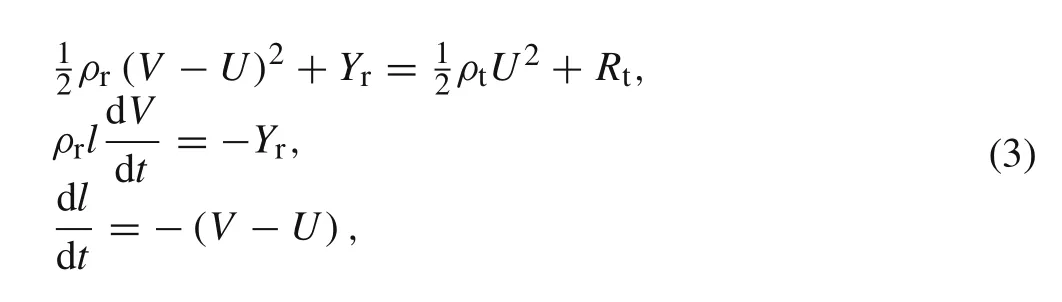
whereρris the density of the rod and is assumed to be constant,Yris the dynamic yield strength of the rod,andlis the length of the nondeforming part of the rod.After that,many researchers systematically studied the strength effect,theL/D(ratio of length to diameter of rod)effect and the terminal phase,and so on.
For a given rod with constant length,we care how deep it can penetrate the target,i.e.,the penetration efficiency.The penetration efficiency is defined as

i.e.,the increment ratio of the penetration depthPto the erosion length of rod.According to Eq.(2),the penetration efficiency predicted by the incompressible model is
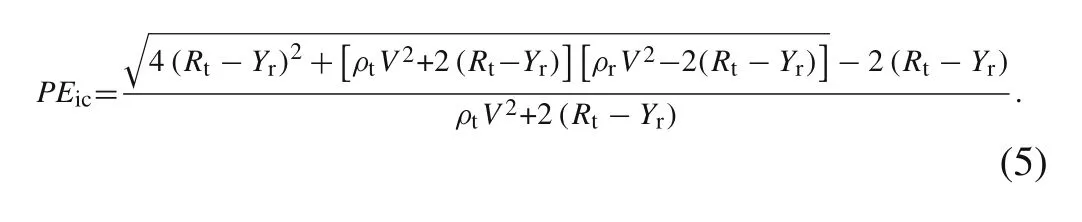

However,in the case of hypervelocity penetration,the pressure at the rod/target interface is extremely high and the volumetric strain of rod or target is especially significant,so the incompressible assumption does not apply.Even if in the steady phase,the shockwave may appear in the rod or target.Besides,the incompressible Bernoulli equation is unable to deal with the process from the initial state or the shockwave to the stagnation point.It compels us to use the compressible Bernoulli equation instead of the incompressible Bernoulli equation,accounting for the internal energy of the rod and target.
It is known that Haugstad and Dullum[7]developed a complete compressible model firstly,with considering the shockwave and internal energy.They used the Murnaghan equation of state(EOS)to describe the relation between the pressure and density.AtV≥10 km/s,there was a reduction in penetration depth of 10%–20%compared to the HTP prediction for the copper jet penetrating aluminum/lead targets,and for the Plexiglas target a full 35%reduction was predicted.Unfortunately,Murnaghan EOS was originally proposed to describe the relation between the bulk modulus and pressure in a quasi-static high pressure state.In contrast,Haugstad and Dullum[7]fitted the Murnaghan EOS with the Hugoniot curves to get the empirical constants,so the values were taken into account for the shock property.In any event,it is worthy to doubt the applicability of Murnaghan EOS in describing the isentropic process from the shockwave to the stagnation point.
In addition,Flis and Chou[8]used the Mie-Grüneisen EOS in the compressible model and extended it to the case of a stretching jet penetration.Regarding a steady copper jet,the difference in penetration depth was up to 20%compared to the HTP prediction if the compressibility of the jet and target material was significantly different.Comparatively,regarding the stretching copperjet,up to a 50%reduction was predicted if the target material is very compressible.Here the Mie-Grüneisen EOS is in the form of
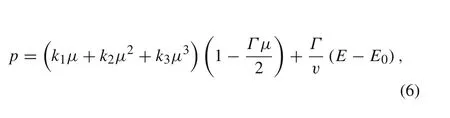
wherep,E,andv≡ 1/ρare pressure,internal energy,and specific volume,respectively.μ≡ρ/ρ0− 1 is strain andΓ≡v(∂P/∂E)vis the Grüneisen parameter.k1,k2,andk3are the material constants fitted with the Hugoniot curves.Basically,the Mie-Grüneisen EOS here is not completely self-consistent with the conditions on the shockwave discontinuity.
There was a model developed by Backofen[9]that accounts for the compressibility when the flow is supersonic,based on the Hugoniot curve of a linear shock velocity particle velocity relation.
Also,Federov and Bayanova[10]used a linear shock velocity-particle velocity relation to describe the shockwave and adopted the Tate Hugoniot,i.e.,the Murnaghan EOS,to deal with the is entropic process from the initial state or the shockwave to the stagnation point.They arranged the equations into the equation of pressure-equilibrium across the jet/target interface about the penetration velocity,avoiding the numerical iterative process.
Then,Osipenko and Simonov[11]used another form of Mie-Grüneisen EOS in the compressible model
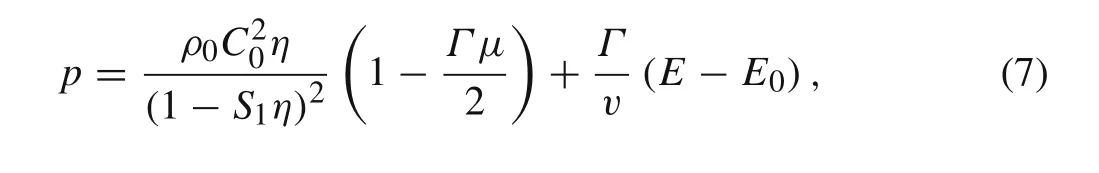
whereC0isbulk sound speed,η≡(v0−v)/v0is volumetric strain andS1is the slope of the linear shock velocity-particle velocity relation.The Mie-Grüneisen EOS is theoretically derived from the Hugoniotcurve while not fitted with it.Thus,the EOS is completely self-consistent with the conditions on the shockwave discontinuity.
The EOS described above all relies on the same form of the Hugoniot relation,i.e.,a linear dependence of shock velocity on particle velocity.In addition,Flis[12]extended the compressible model proposed by Osipenko and Simonov[11]to a quadratic dependence of shock velocity on particle velocity and to a specific heat that varies with temperature and volume.Moreso,Flis[12]also performed a CTH code(the Eulerian shock physics analysis package developed by Sandia National Laboratories)computation to compare with the model.The results predicted by the compressible model were in good agreement with the CTH simulations,showing the validity of the model.This model[13]was further modified by Flis[12]to account for the target resistanceRtby introducing an initial pressure that is a fixed multiple of the target’s plastic flow strength.Similarly,CTH simulations were conducted to compare with the compressible model with or without shockwave,and the incompressible model.Only the results from the compressible model with shockwave were in agreement with the CTH simulations when the compressibility of the jet and target material was different.Thus the compressibility of the rod/target materials and shockwave could not be neglected in hypervelocity penetration.
A proposal by Flis[14]was for a simplified analytical model for predicting the first-order effect of compressibility in hypervelocity jet penetration.He made two simplifying assumptions:the presence of shocks is neglected and each material’s pressure-volume isentrope is approximated by its Hugoniot curve.So the resulting equations are reduced to a form that only depends on the pressure at the rod/target interface.The iterative process is replaced by the root-finding technique and no numerical integrations are required.
The main use of the penetration models introduced above is in the long-rod penetration and penetration of the jet from shaped charge.Shaped charge is a cylindrical explosive charge with a hollow cavity at one end and a detonator at the other.The cavity is usually lined with a metallic liner made of copper,steel,aluminum,etc.Detonation of the explosive charge collapses the liner material in the form of a jet,whose tip may attain a velocity in excess of 10 km/s.
For example,a simple shaped charge configuration with length of 0.15 m,diameter of 0.08 m and copper liner is typically accepted in some engineering and military designs[15].The tip velocity of the copper liner is 8 km/s.
Developed by Walker et al.[16]was a hypervelocity fragment launcher based on an inhibited shaped charge,which launches an aluminum jet at 11.2±0.2 km/s.They performed experimental and computational work to study the jet.
Then Walters and Scheffler[17]added an air cavity wave shaper overlapping the liner to increase the tip velocity of the coherent portion of the liner to about 10.0 km/s,with hypervelocity jet particles traveling in front of the tip with a velocity of about 14 km/s.The baseline case was a standard 7.5-cm-diameter liner with a tip velocity of 8.0 km/s.
In the present work,we adopt the compressible penetration model of Flis[13],i.e.,the shock velocity-particle velocity Hugoniot condition is linear or quadratic,and apply this Hugoniot condition to both the shockwave discontinuity and the Mie-Grüneisen EOS.The compressible Bernoulli equation is employed to describe the process from the initial state or shockwave to the stagnation point,taking account of the internal energy of the rod and target and the target resistanceRt.Besides,we also take account of rod strength by introducing an initial pressure to study the effect of compressibility on rod penetration at 3 km/s<V<12 km/s.To systematically study the effect of compressibility in different metallic rod-target combinations,we construct three cases,i.e.,the penetrations by the more compressible rod into the less compressible target,rod into the analogously compressible target and the less compressible rod into the more compressible target.These three cases are examples of the penetrations by 6061-T6 Al rod into tungsten heavy alloy(WHA)target,copper rod into 4340 Steel and WHA rod into 6061-T6 Al target,respectively.We analyze the effects of volumetric strain,internal energy and strength on the penetration efficiency by systematically comparing the compressible model,the incompressible model and the HTP.
2 Basic theory
The compressible penetration model is derived in coordinates moving at the penetration velocityU.The flow field near the rod/target interface is schematically shown in Fig.1.The subscripts r and t represent the rod and target,respectively.The subscripts 0,1,and 2 represent the states before the shockwave,after the shockwave and at the stagnation point(i.e.,rod/target interface),respectively.
The linear or quadratic shock velocity-particle velocity Hugoniot condition is adopted to treat the shockwave discontinuity.The Mie-Grüneisen EOS and the isentropic condition are employed to deal with the isentropic process from the initial state or shockwave to the stagnation point.The equation of pressure equilibrium across the rod/target interface is used to update the penetration velocityU.The whole process is repeated until convergence.
The details of the compressible model are given in the Appendix.
In the compressible model,the initial state 0 is supposed to be known,i.e.,the penetration velocityUis known.However,Flis[13]did not explain how to evaluate the initial penetration velocityU.For a givenV,according to Eq.(2),we suppose the penetration velocity to be
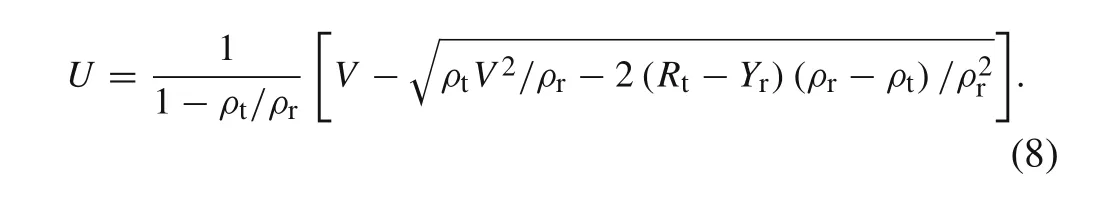
Fig.1 Flow field in moving coordinates and flow states[13]
Ifthe penetration velocityU′andU′are known at the impact velocity ofV′andV′,respectively,andV′andV′are close toV,we use linear interpolation instead of Eq.(8)
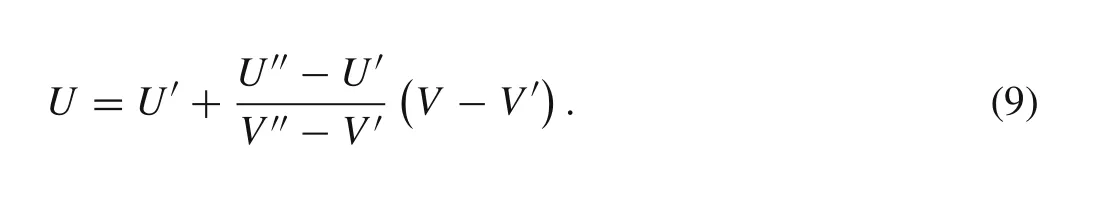
The penetration velocityUcalculated by the linear interpolation is much closer to the true value,increasing the efficiency of the program.
To be noted is that Flis[13]took the rod strength as zero in the compressible model,i.e.,he did not consider the effect of the rod strength.In the following work,we will consider the effect of rod strength.
The flowchart for the program is shown in Fig.2.The process is as follows:to set the initial penetration velocityUaccording to the value of impact velocityV;to set the initial states for the rod and target;to handle the shockwave discontinuity and the isentropic process from the shockwave to the stagnation point to get the physical properties of the rod and target at the stagnation point;to update the penetration velocityUbecause the pressure equilibrium across the rod/target interface is not satisfied;and to repeat the above process until the pressure equilibrium is satisfied,i.e.,the penetration velocityUconverges.
There is no experimental data for hypervelocity long-rod penetration.However,Flis[12,13]conducted numerical simulations to validate the compressible modelwith and without the target resistance,respectively.Flis[12]conducted CTH simulations of strengthless copper jets penetrating strengthless polymethyl methacrylate(PMMA)targets to verify the compressible model with and without shockwave and only the results from the compressible model with shockwave were in excellent agreement with the simulations.In the latter work,Flis[13]conducted CTH simulations of strengthless copper jets penetrating steel targets with different yield strengths,strengthless aluminum jets penetrating PMMA targets and strengthless PMMA jets penetrating aluminum targets and the comparison of model predictions with numerical simulations showed excellent agreement.These simulations have already clearly shown the validity of the compressible model.So we do not conduct extra numerical simulations in the following work.
To validate the program,we repeat two cases by Flis[13]without considering the rod strength,i.e.,PMMA rod penetrating semi-infinite Al target(Yr=0,Rt=4.8×0.3 GPa)and Al rod penetrating semi-infinite PMMA target(Yr=0,Rt=4.0×0.07 GPa).Material properties for Aluminum and PMMA are shown in Table 1.

Fig.2 Flowchart for the program
The ratios of penetration efficiency predicted by the compressible model to the hydrodynamic limit are shown in Fig.3.The results calculated by our program are in great agreement with that by Flis[13],which completely validates the program.In both of the two cases,the penetration efficien-cies predicted by the compressible model do not approach the hydrodynamic limit with increasing impact velocity.In the case of the PMMA rod penetrating a semi-infinite Al target,the penetration efficiency predicted by the compressible model is obviously higher than the hydrodynamic limit with increasing impact velocity andPEc/PEh=1.091 atV=10 km/s.Comparatively,in the case of the Al rod penetrating a semi-infinite PMMA target,the penetration efficiency predicted by the compressible model is obviously lower than the hydrodynamic limit with increasing impact velocity andPEc/PEh=0.890 atV=10 km/s.
In the above cases,the rod strength is zero.In order to understand the effect of rod strength on the penetration,we further calculate the cases of the PMMA rod penetrating a semi-infinite Altarget(Yr=0.12 GPa,Rt=4.8×0.3 GPa)and the Al rod penetrating a semi-infinite PMMA target(Yr=0.5 GPa,Rt=4.0×0.07 GPa)with considering the rod strength.The rod strength would decelerate the rod by the magnitude of 2Yr/(ρC)at the end of the rod within one unload,i.e.,2Yr/(ρ0C0)=70 m/s for the Al rod and 2Yr/(ρ0C0)=88 m/s for the PMMA rod.The magnitude is negligible compared to the initial impact velocity which is some km/s,so we will not consider the deceleration of the rod in the following work.The ratios of penetration efficiencies with and without rod strength to the hydrodynamic limit are shown in Fig.4.
Figure 4 shows that the rod strength increases the penetration efficiency a little.However,in the case of the PMMA rod penetrating a semi-infinite Altarget,the penetration resistance of the Al target(Rt=4.8×0.3 GPa)is much higher than the dynamic yield strength of the PMMA rod(Yr=0.12 GPa),so the strength of the PMMA rod has little effect on penetration efficiency.In the case of the Al rod penetrating a semi-infinite PMMA target,the penetration resistance of the PMMA target(Rt=4.0×0.07 GPa)is lower than the dynamic yield strength of the Al rod(Yr=0.5 GPa),but basically they are comparative.AtV<7 km/s,the strength of the Al rod obviously affects the penetration efficiency.So,when the dynamic yield strength of the rod is larger than or comparative to the penetration resistance of the target,the effect of rod strength on the penetration efficiency cannot be neglected.
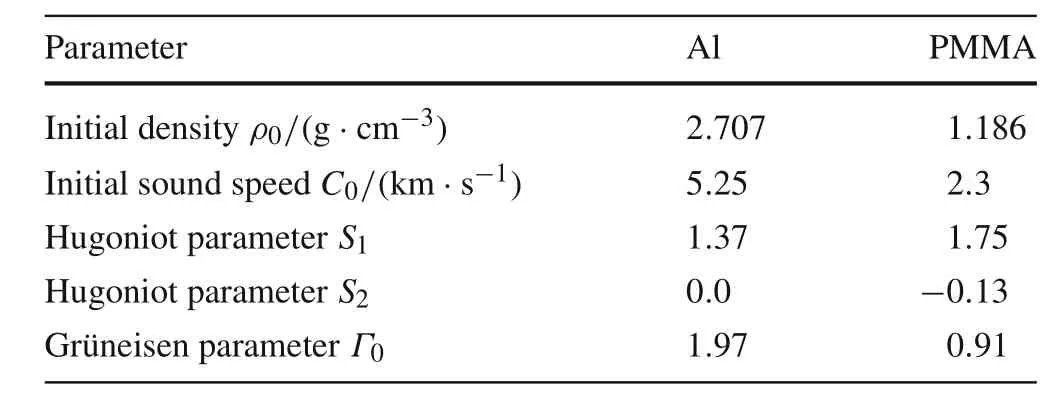
Table 1 Material properties for aluminum and PMMA[13]

Fig.3 Ratio of predicted penetrations to the hydrodynamic limit for strengthless Al rod penetrating PMMA and strengthless PMMA rod penetrating Al[13]

Fig.4 Ratio of predicted penetrations to the hydrodynamic limit for Al rod penetrating PMMA and PMMA rod penetrating Al
3 Parameter discussion on the compressible model
According to Eq.(A24),the pressure at the stagnation point in the compressible model is

If we ignore the internalenergy and strength of the rod and target and only consider the kinetic energy,it implies that we use the real density at the rod/target interface in the hydrodynamic limit.So,the penetration efficiency of the modified HTP is

wherekr≡ρ2r/ρ0r=1/(1−η2r)andkt≡ρ2t/ρ0t=1/(1−η2t)are the ratios of the density at the interface to the initial density of the rod and target,respectively,which generally reflects the magnitude of the volumetric strain.So the kinetic energy is dominated by the volumetric strain with constant impact velocity.
The real density at the rod/target interface is used to calculatePE∗h,while the initial density is used to calculatePEhin the HTP.So the difference betweenPE∗handPEhis attributed to the difference between the volumetric strain of the rod and target at the rod/target interface.The more deviation ofPE∗h/PEhfrom 1 represents a larger difference between the volumetric strain of the rod and target.
If we ignore the internal energy of the rod and target,and only consider the kinetic energy and strength in Eq.(A25),it means that we use the real density at the rod/target interface but not the initial one in the incompressible model.Thus,the penetration efficiency of the modified incompressible model is




Table 2 Penetration efficiencies of different models
All penetration efficiencies defined above are summarized in Table 2.

4 The effect of compressibility on the penetration
In the case of hypervelocity penetration,the pressure at the rod/target interface,volumetric strain,and internal energy of the rod and target become larger with increasing impact velocity.Different material have different compressibility,which may affect the penetration thoroughly.
The material properties of 6061-T6 Al[18],copper[13],4340 Steel[19],and tungsten heavy alloy(WHA)[19]are shown in Table 3.The Hugoniot curves for these material are plotted in Fig.5 according to Eq.(A4).As seen in the figure,with the same volumetric strain,we have the equation of the impact pressurepH(WHA)>pH(4340Steel)≈pH(Cu)>pH(6061-T6Al).So,under the impact condi-tion,6061-T6 Al is the most compressible,WHA is the least compressible,and 4340 Steel and copper are analogously compressible and their compressibility is intermediate between 6061-T6 Al and WHA.
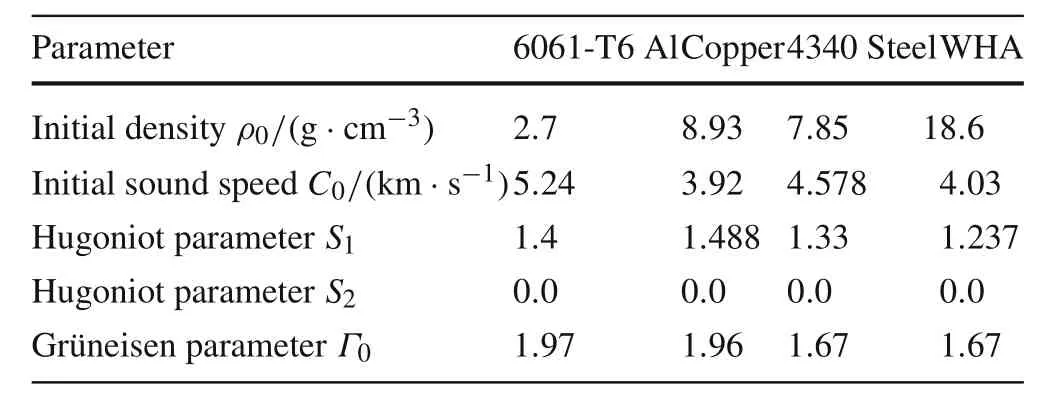
Table 3 Material properties[16,18,19]
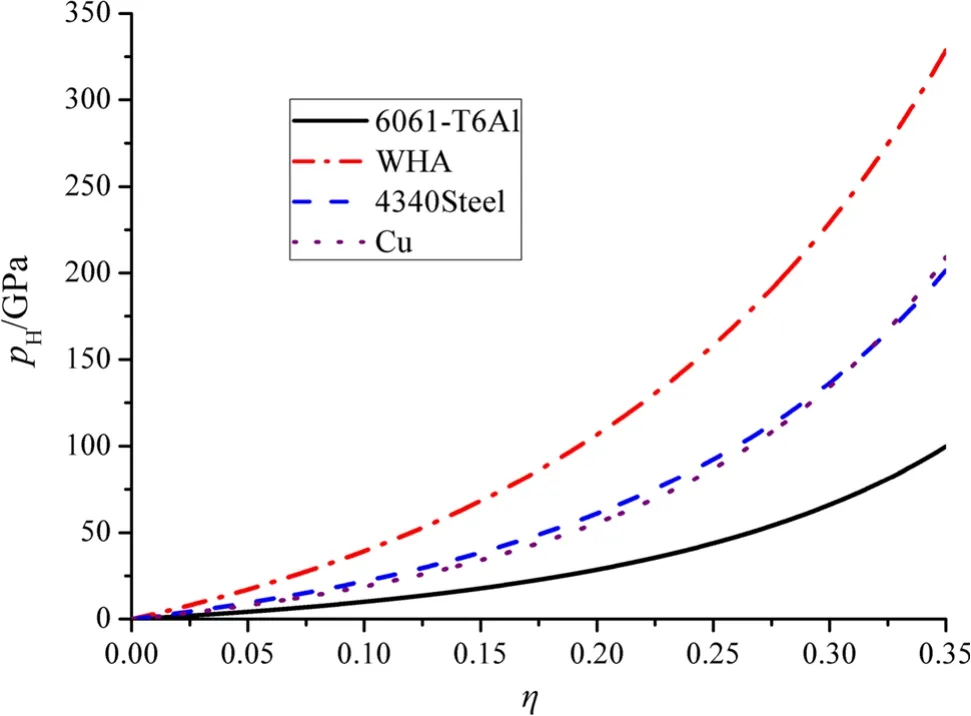
Fig.5 Hugoniot curves for 6061-T6 Al[18],copper[13],4340 Steel[19],and WHA[19]
4.1 Penetration by the more compressible rod into the less compressible target
The 6061-T6 Al is much more compressible than WHA.We employ the compressible model and the incompressible model to calculate the penetration by the 6061-T6 Al rod into a semi-infinite WHA target at the impact velocity of 3−12 km/s withYr=0.5 GPa andRt=4.5 ×1.67 GPa.The ratios of penetration efficiencies predicted by the compressible model and the incompressible model to the hydrodynamic limit are shown in Fig.6.Orphal and Anderson[20]used CTH code to simulate the same penetration by 6061-T6 Al into a semi-infinite WHA target at the impact velocity of 3−8 km/s and got the linearU−Vrelation.We derive the penetration efficiency from this relation using Eq.(4)and the result is also plotted in Fig.6.
As seen in Fig.6,the result of the compressible model agrees with the CTH simulation better at higher impact velocity within 5−8 km/s.AtV=8 km/s,we havePEc/PEh=1.002,PEic/PEh=0.923,and(PEc−PEic)/PEh=7.9%.AtV=12 km/s,we havePEc/PEh=1.059,PEic/PEh=0.966,and(PEc−PEic)/PEh=9.3%.The penetration efficiency predicted by the compressible model is obviously higher than that predicted by the incompressible model.It indicates that the effect of compressibility is to enhance the penetration ability of the 6061-T6 Al rod.
The pressure at the rod/target interface for the 6061-T6 Al rod penetrating WHA is shown in Fig.7.AtV<6 km/s,the pressure predicted by the compressible model is higher than that predicted by the incompressible model,but the difference is quite small.However,at higher impact velocity,the pressure increment attributed to the compressibility is larger.AtV=8 km/s,we havep2c=56.0 GPa andpic=47.8 GPa,and the pressure predicted by the compressible model is 8.2 GPa higher than that predicted by the incompressible model.Comparatively,atV=12 km/s,we havep2c=135.0 GPa andpic=104.4 GPa,and the pressure predicted by the compressible model is30.6 GPa higher than that predicted by the incompressible model.
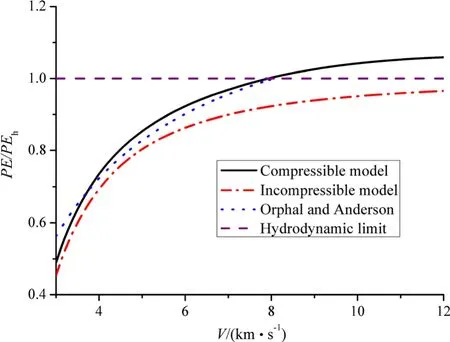
Fig.6 Ratio of predicted penetration to the hydrodynamic limit for 6061-T6 Al rod penetrating WHA[20]
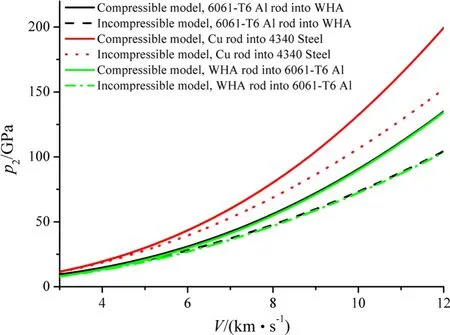
Fig.7 Pressure at the rod/target interface for different rod-target combinations
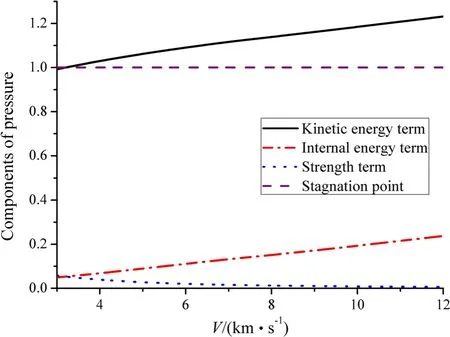
Fig.8 The pressure components of 6061-T6 Al rod when it penetrates WHA
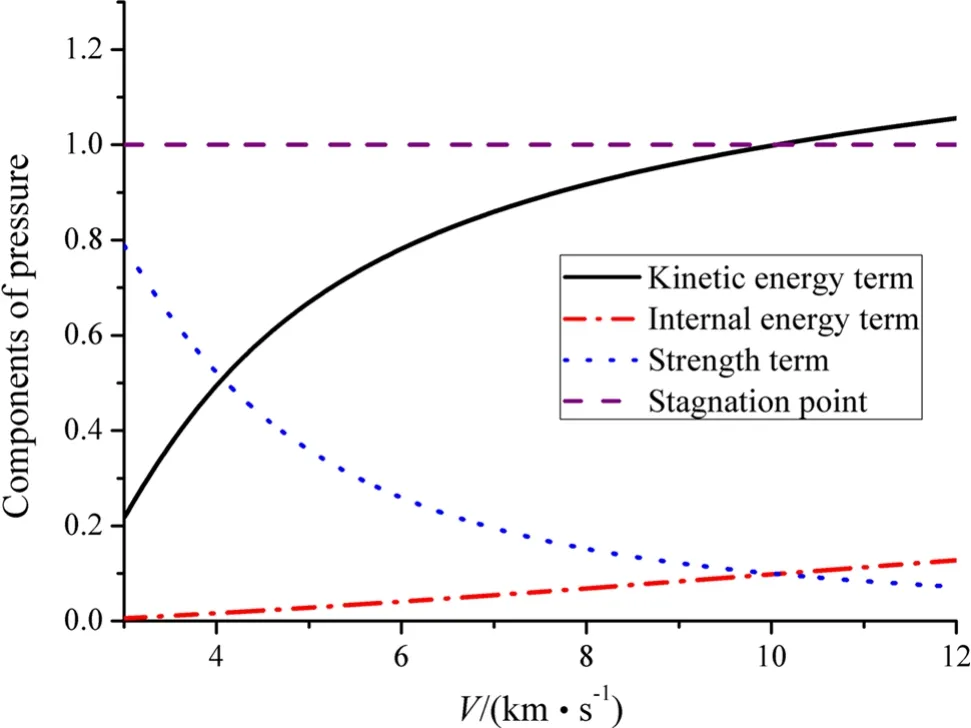
Fig.9 The pressure components of WHA target when it is penetrated by 6061-T6 Al rod
The terms of the kinetic energy,internal energy and strength of the 6061-T6 Al rod and WHA target are shown in Figs.8 and 9,respectively.At higher impact velocity,the kinetic energy term and internal energy term become stronger while the strength term becomes weaker.Regarding the 6061-T6 Al rod,the kinetic energy term is always stronger than the terms of the internal energy and strength.While regarding the WHA target,its kinetic energy term is stronger than the terms of the internal energy and strength only atV>4.1 km/s.In addition,the kinetic energy of the 6061-T6 Al rod is always stronger than that of the WHA target,for example,atV=12 km/s,we haveKr=123.1%andKt=105.6%.Because the penetration resistance of the WHA targetRt=4.5×1.67 GPa is very strong,its strength term is strong.AtV=7 km/s andV=12 km/s,we haveSt=19.5%andSt=7.2%,respectively.However,the dynamicyield strength of the6061-T6 AlYr=0.5 GPa is much weaker than the penetration resistance of the target,and thus the strength term of the rod is very weak.Comparatively,at the same velocities,i.e.,atV=7 km/s andV=12 km/s,we haveSr=1.6%andSr=0.6%,respectively.Simultaneously,the internal energy term of the 6061-T6 Al rod is always stronger than that of the WHA target,for example,atV=12 km/s,we haveIr=23.8%andIt=12.8%,respectively.

Fig.10 Ratio of predicted penetration to the hydrodynamic limit for the 6061-T6 Al rod penetrating WHA

In summary,the larger volumetric strain of the rod enhances the penetration ability of the rod,the stronger strength of the target enhances the anti-penetration ability of the target,and the stronger internal energy of the rod weakens the penetration ability of the rod.However,the vol-umetric strain dominates in the penetration,and thus results inPE∗h>PE∗
ic>PEc>PEic.

Fig.11 Ratio of predicted penetration to the hydrodynamic limit for copper rod penetrating 4340 Steel
4.2 Penetration by rod into the analogously compressible target
The difference between the compressibility of copper and 4340 Steel is quite small.We use the compressible model and the incompressible model to calculate the penetration by the copper rod into a semi-infinite 4340 Steel target at the impact velocity of 3−12 km/s withYr=0 andRt=4.5×0.792 GPa.The strength of copper is low and copper is a common material of the jet,so we takeYr=0.The ratios of penetration efficiencies predicted by the compressible model and the incompressible model to the hydrodynamic limit are shown in Fig.11.The value of(PEc−PEic)/PEhis in the range of 0.4%–1.4%,and it implies that in this case,the prediction of the compressible model agrees with that of the incompressible model and both of them approach the hydrodynamic limit at higher velocity.
The pressure at the rod/target interface for the copper rod penetrating 4340 Steel is shown in Fig.7.AtV<6 km/s,the pressure predicted by the compressible model is higher than that predicted by the incompressible model,but the difference is very small.However,at higher impact velocity,the pressure increment attributed to the compressibility becomes greater.AtV=8 km/s,we havep2c=80.3 GPa andpic=68.8 GPa,and the pressure predicted by the compressible model is 11.5 GPa greater than that predicted by the incompressible model.Similarly,atV=12 km/s,p2c=199.5 GPa,andpic=152.4 GPa,and the pressure deviation is47.1 GPa.Basically,the material compressibility is to increase the pressure at the rod/target interface.However,as the compressibility difference between the copper and 4340 Steel is very small,the penetration efficiency is not affected.
The terms of the kinetic energy,internal energy and strength of the copper rod and 4340 Steel target are shown in Figs.12 and 13,respectively.The kinetic energy terms of the copper rod and 4340 Steel target are distinctly stronger than their internal energy term and strength term.With increasing impact velocity,the kinetic energy term and internal energy term become stronger while the strength term becomes weaker.The strength term of the 4340 Steel is notable at lower impact velocity while atV>7 km/s it becomes weak.The kinetic energy term of the copper rod is stronger than that of the 4340 Steel target.But,at higher impact velocity,the difference between them becomes smaller,e.g.,Kr=119.4%andKt=117.2%atV=12 km/s.Similarly,the internal energy of the copper rod differs little from that of the 4340 Steel target,for example,we haveIr=19.4%andIt=20.0%atV=12 km/s.
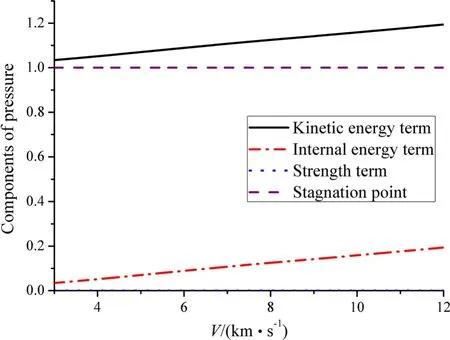
Fig.12 The pressure components of the copper rod when it penetrates 4340 Steel

Fig.13 The pressure components of 4340 Steel target when it is penetrated by the copper rod

Fig.14 Ratio of predicted penetration to the hydrodynamic limit for the copper rod penetrating 4340 Steel
In summary,the volumetric strain and internal energy of the rod match that of the target but the stronger strength of the target enhances its anti-penetration ability,and thus results inPE∗h>PE∗ic≈PEc≈PEic.AtV>7 km/s,the strength terms of the rod and target become weaker,soPEcandPEicapproach the hydrodynamic limit.
4.3 Penetration by the less compressible rod into the more compressible target
Different from Sect.4.1,here we check the penetration by WHA rod into a semi-infinite 6061-T6 Al target at the impact velocity of 3−12 km/s withYr= 2.0 GPa andRt=4.5×0.3 GPa.Figure 15 shows the ratios of penetration efficiencies predicted by the compressible model and the incompressible model to the hydrodynamic limit.Because ofYr>Rt,the incompressible model prediction is greater than but approaches the hydrodynamic limit atV>6 km/s.AtV=8 km/s,we havePEc/PEh=0.944,PEic/PEh=1.007,and(PEc−PEic)/PEh= −6.3%.Comparatively,atV=12 km/s,we havePEc/PEh=0.924,PEic/PEh=1.003,and(PEc−PEic)/PEh=−7.9%.The penetration efficiency predicted by the compressible model is obviously lower than the incompressible model prediction.It indicates that the compressibility of the 6061-T6 Al target enhances its anti-penetration ability.
The pressure at the rod/target interface for WHA rod penetrating 6061-T6 Al target is shown in Fig.7.AtV<6 km/s,the pressure predicted by the compressible model is higher than the incompressible model prediction,but the deviation may be ignored.With increasing impact velocity,the pressure increment attributed to the compressibility increases.AtV=8 km/s,we havep2c=54.9 GPa,andpic=46.8 GPa,and the pressure predicted by the compressible model is 8.1 GPa higher than that predicted by the incompressible model.AtV=12 km/s,p2c=134.3 GPa,andpic=103.5 GPa,and the pressure deviation is 30.8 GPa.
The terms of the kinetic energy,internal energy and strength of the WHA rod and 6061-T6 Al target are shown in Figs.16 and 17,respectively.The kinetic energy terms of the WHA rod and 6061-T6 Al target are stronger than their internal energy terms and strength terms.With increasing impact velocity,the terms of kinetic energy and internal energy become stronger while the strength term becomes weaker.Besides,the kinetic energy term of the WHA rod is always weaker than that of the 6061-T6 Al target.In contrast,the internal energy term of the WHA rod is always weaker than that of the 6061-T6 Al target.AtV=12 km/s,we haveKr=110.6%andKt=121.9%,butIr=12.5%andIt=23.6%.Comparatively,the strength terms of both the WHA rod and 6061-T6 Al target are quite weak atV>7 km/s.

Fig.15 Ratio of predicted penetration to the hydrodynamic limit for WHA rod penetrating 6061-T6 Al
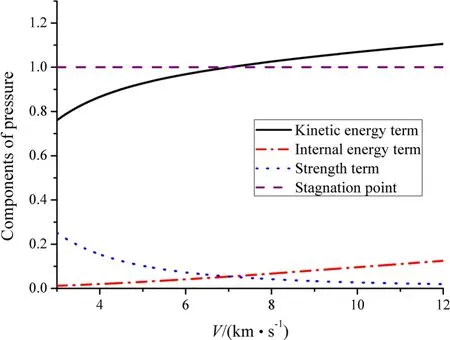
Fig.16 The pressure components of the WHA rod when it penetrates 6061-T6 Al

Fig.17 The pressure components of the 6061-T6 Al target when it is penetrated by the WHA rod

In summary,the larger volumetric strain of the target enhances its anti-penetration ability while its stronger internal energy weakens its anti-penetration ability.The stronger strength of the rod enhances its penetration ability.As the volumetric strain dominates in the penetration,we havePE∗h<PE∗ic<PEc<PEic.
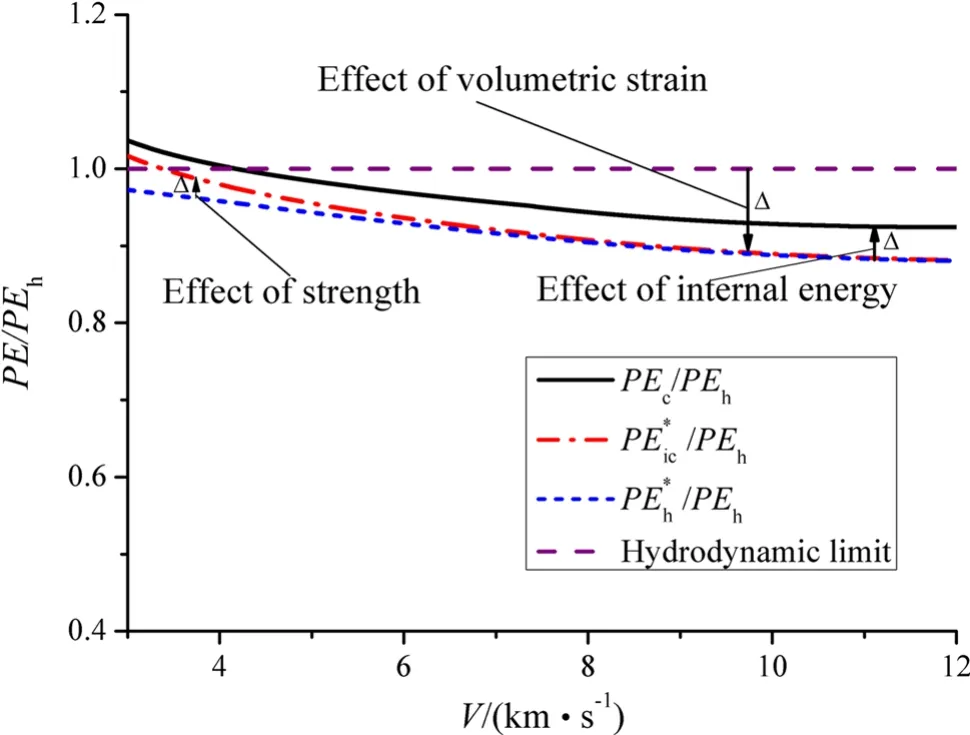
Fig.18 Ratio of predicted penetration to the hydrodynamic limit for the WHA rod penetrating 6061-T6 Al
5 Analyses on the main parameters
5.1 Pressure at the rod/target interface
In the compressible model,the pressure at the rod/target interface is
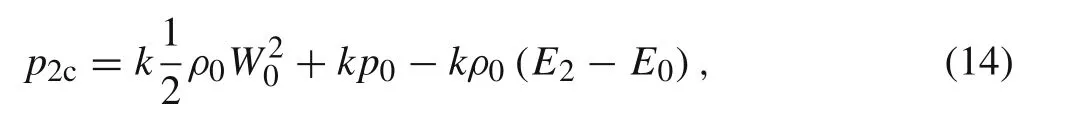
wherek≡ρ2/ρ0is the ratio of the density at the rod/target interface to the initial density.The pressure at the rod/target interface consists of the kinetic energy,strength and internal energy.
While in the incompressible model,the pressure at the rod/target interface is


Fig.19 Ratio of pressure at the rod/target interface predicted by the compressible model to the incompressible model for three cases
The pressure at the rod/target interface consists of the kinetic energy and strength,not including the internal energy.
With comparing Eqs.(14)and(15),we know that the kinetic energy and strength in the compressible model are the product of that in the incompressible model andk.So the volumetric strain must increase the pressure at the rod/target interface.However,the internal energy ofp2cwill decrease the pressure at the rod/targetinter face.Referring to the above three cases,the kinetic energy term is much larger than the internal energy term,and thus the compressibility is to increase the pressure at the rod/target interface in the compressible model over that in the incompressible model.At higher impact velocity,the volumetric strain is larger and the pressure increment attributed to the compressibility is higher.
Figure 7 isredrawn in Fig.19,with the vertical axes as normalized pressure at the rod/target interface,that is,p2c/pic.As shown in Fig.19,the normalized pressures are larger than 1 and increase with increasing impact velocity for all three cases.The compressibility is to increase the pressure and the effect is stronger at higher velocity.
Comparing the penetrations by the 6061-T6 Al rod into the WHA target(case 1)and by the WHA rod into the 6061-T6 Al target(case 3),as shown in Fig.7,the pressures at the rod/target are almost the same in these two cases.For example,atV=12 km/s,we havep2c=135.0 GPa andpic=104.4 GPa in case 1,andp2c=134.3 GPa andpic=103.5 GPa in case 3.Comparatively,in the penetration by copperrod into the 4340 Steeltarget(case 2),we havep2c=199.5 GPa andpic=152.4 GPa atV=12 km/s.The pressure at the rod/target interface predicted by the compressible model is higher than the prediction of the incompressible model.
5.2 Strength
In the incompressible model,the kinetic energy is proportional to the square of the impact velocity,while the strength is a constant.So with increasing impact velocity,the kinetic energy term obviously increases while the strength term decreases,resulting in that the penetration efficiency approaches the hydrodynamic limit,e.g.,cases 1 and 3 as shown in Figs.6 and 15,respectively.However,as the strength of WHA is much larger than that of 6061-T6 Al,the penetration efficiency slowly approaches the hydrodynamic limit from below in case 1 whilst fast approaches the hydrodynamic limit from above in case 3.
As seen in Fig.10,at 3 km/s<V<12 km/s the strength has an assignable effect on the penetration efficiency,because the strength of the WHA target is extremely high in case 1.Similarly,as seen in Fig.14,the strength of the target has an effect on the penetration efficiency atV<7 km/s and the effect weakens with increasing impact velocity.As seen in Fig.18,the effect of strength is negligible,because the strength of the rod and target is comparative.
In the present work,the target resistanceRtis a fixed multiple of the target’s plastic flow strength.ButRtis not an intrinsic material parameter.In the range of ordnance velocity,Rtis affected by the plastic flow strengthσY,elastic properties and the extent and rate of plastic deformation of the target.Rtcan be expressed in terms of these corresponding parameters by means of an exact solution of the corresponding problem.For applicability and simplicity,Eichelberger[3],Alekseevskii[4]and Tate[5]tookRtas a fixed multiple ofσY.Tate]estimateda spherical cavity expansion and Rosenberg et al.[22]esti-from a cylindrical cavity expansion,whereEandνare Young’s modulus and Poisson’s ratio of the target,respectively.For example,Anderson and Walker[23]conducted numerical simulations to study the effects of strain hardening,strain-rate hardening and thermal softening on penetration response.In addition,Anderson et al.[24]conducted numerical simulations and observed thatRtdecreases with impact velocity,and this is a consequence of both the residual phase of penetration and variations in the size of the plastic zone field.Then,too,Rosenberg and Dekel[25]used 2-D simulations of penetration by strengthless tungsten alloy rod into steel target to get the relationship
The researches introduced above are in the range of ordnance velocity.For hypervelocity penetration,there is no systematic study aboutRt.Even so,Flis[13]adjusted the value ofRtto make the compressible model to fit results of numerical simulations over the range of up to 12 km/s.It is our future work to systematically study theRtin hypervelocity penetration.
As shown in the above analyses,the effect of strength on penetration efficiency becomes weaker with increasing impact velocity.So in the higher velocity range,e.g.,V>7 km/s,the strength of the rod and target can be neglected if the initial strength is not extremely strong.
5.3 Internal energy
The internal energy of the rod and target material has a negative effect on the pressure at the rod/target interface in Eq.(14).In all three cases,if the material is more compressible,the internal energy is higher.Meanwhile,the internal energy becomes higher with increasing impact velocity.As seen in Figs.10 and 18,the internal energy has an influence on the penetration efficiency at 3 km/s<V<12 km/s.Especially,the effect of the internal energy on the penetration efficiency will be stronger at higher impact velocity and this is opposite to the trend of the strength effect.In case 1,the internal energy of the 6061-T6 Al rod is larger than that of the WHA target,soPE∗icis greater thanPEc,i.e.,the higher internal energy of the rod weakens its penetration ability.In case 3,the internal energy of the WHA rod is smaller than that of the 6061-T6 Al target,soPE∗icis lower thanPEc,i.e.,the higher internal energy of the target weakens its antipenetration ability.
If the rod and target are analogously compressible,the internal energy of the rod and target are almost equal to each other with the same volumetric strain.In this case,if we add the internal energy into pressure equilibrium at the rod/target interface of the incompressible model and multiply the equation by the density ratiok,the same form of pressure equilibrium at the rod/target interface in the compressible model is derived.So,if the rod and target are analogously compressible,the penetration efficiency predicted by the compressible model is the same as that predicted by the incompressible model.
Although the pressure increment attributed to the compressibility in case 2 is higher than that in cases 1 and 3,compressibility has little effect on the penetration efficiency.This is attributed to the fact that copper and 4340 Steel are analogously compressible and thus the volumetric strain and internal energy of copper are almost the same with that of 4340 Steel,respectively,i.e.,the effect of compressibility on the rod is almost the same with the target.As shown in Fig.11,with increasing impact velocity,the penetration efficiency predicted by the compressible model differs little from the incompressible model prediction and both of them approach the hydrodynamic limit.
It is worth mentioning that,the internal energy term of the rod and target linearly increase with the impact velocity in all cases.We do not analyze this relation in the present work.However,the compressible model may be further simplified to get an analytical solution by using this relation and neglecting the strength term in the higher velocity range,e.g.,V>7 km/s of the hypervelocity penetration.

Fig.20 Ratio of penetration depth predicted by the compressible model to the incompressible model for three cases
5.4 Penetration efficiency
In cases 1 and 3,the penetration efficiencies predicted by the compressible model do not approach the hydrodynamic limit with increasing impact velocity.In case 1,we havePEc/PEh= 1.059,PEic/PEh= 0.966,and(PEc−PEic)/PEh=9.3%atV=12 km/s.Comparatively,In case 3,we havePEc/PEh=0.924,PEic/PEh=1.003,and(PEc−PEic)/PEh=−7.9%atV=12 km/s.
Ratios of penetration depth predicted by the compressible model to the incompressible model are shown in Fig.20 for three cases.HerePcandPicrepresent the penetration depths predicted by the compressible model and the incompressible,respectively.The normalized predicted depths do not change in the same trend for different rod-target combinations,although the compressibility increases the pressure at the rod/target interface for all three cases.The 6061-T6 Al rod is more compressible than the WHA target and the normalized depth is larger than 1 in case 1.The copper rod and 4340 Steel target are analogously compressible and the normalized depth approximately equals 1 in case 2.The WHA rod is less compressible than the 6061-T6 Al target and the normalized depth is smaller than 1 in case 3.
For the same pressure at the rod/target interface,the volumetric strain of the more compressible material is larger,which enhances the ability of rod penetration or target antipenetration.On the other hand,the internal energy of the more compressible material is also higher,which will weaken the penetration or anti-penetration ability contrarily.However,the volumetric strain matters most and finally the penetration efficiency is to change in the trend dominated by the volumetric strain instead of to approach the hydro-dynamic limit.Pressure equilibrium across the rod/target interface is
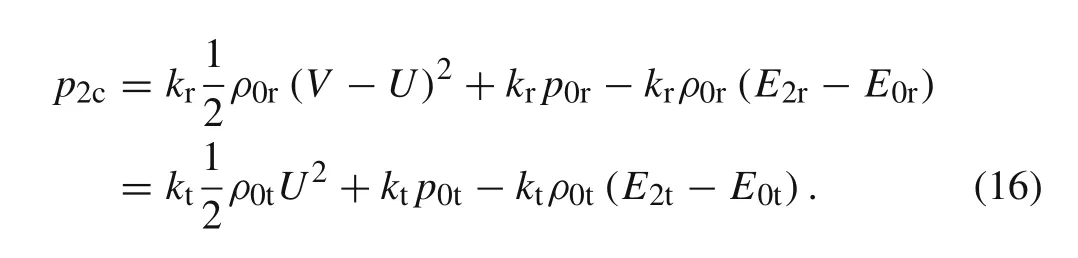
In Eq.(16),if the rod has the properties conducive to improve pressure at the rod/target interface,e.g.,to have larger volumetric strain,higher strength and lower internal energy when material deforms,(V−U)must become smaller andUmust become larger in order to achieve the pressure equilibrium.It implies that the penetration ability of the rod becomes stronger and the penetration efficiency will be improved.In the similar way,if the target has the properties conducive to improve pressure at the rod/target interface,the anti-penetration ability of the target becomes stronger and the penetration efficiency will be reduced.
In summary,we further consider the rod strength in the compressible penetration model in which Flis[13]did not consider the effect of rod strength.In addition,we detail in our study the effects of volumetric strain,internal energy and strength in the compressible model by comparing different instances of penetration efficiency in various modified models.We clearly identify that it is the difference between the compressibility of the rod/target that really affects the penetration efficiency by changing the terms of volumetric strain and internal energy.The effects of volumetric strain and strength are in conflict with the effect of internal energy.However,the volumetric strain dominates in the variation of the penetration efficiency.
6 Conclusions
In the case of hypervelocity penetration,the incompressible assumption does not apply,and the compressible model should be employed.We further take account of rod strength in the compressible model.Meanwhile,we define different instances of penetration efficiency in various modified models and compare these penetration efficiencies to identify the effects of different factors in the compressible model.To systematically study the effect of compressibility in different metallic rod-target combinations,we construct three cases,i.e.,the penetrations by the more compressible rod into the less compressible target,rod into the analogously compressible target and the less compressible rod into the more compressible target.These three cases are examples of the penetrations by the 6061-T6 Al rod into the WHA target,copper rod into the 4340 Steel and the WHA rod into the 6061-T6 Al target,respectively.
Referring to the three cases,the pressure at the rod/target interface predicted by the compressible model is higher than that predicted by the incompressible model.The pressure increment attributed to the compressibility increases with increasing impact velocity.However,what affects the penetration efficiency is not the pressure increment but the difference between the compressibility of the rod and target.
If the compressibility difference between the rod and target is distinct,the volumetric strain of the more compressible material is larger,which enhances the penetration or antipenetration ability.On the other hand,the internal energy of the more compressible material is also higher,which weakens the penetration or anti-penetration ability contrarily.However,the volumetric strain matters most and the penetration efficiency is to change in the trend dominated by the volumetric strain instead of to approach the hydrodynamic limit.
If the rod and target are analogously compressible,the effect of compressibility only increases the pressure at the rod/target interface and has little effect on the penetration efficiency.The penetration efficiency predicted by the compressible model agrees with the incompressible model prediction and approaches the hydrodynamic limit with increasing impact velocity.
AcknowledgementsThe work was supported by the National Outstanding Young Scientist Foundation of China(Grant 11225213)and the Key Subject“Computational Solid Mechanics”of China Academy of Engineering Physics.
Appendix A:Compressible penetration model[13]
Equation of state(EOS)
Taking compressibility into account,an EOS must be used to describe the relation between the internal energy,pressure and density of the material.Here the Mie-Grüneisen EOS is employed

whereE,p,ρ,andv≡ 1/ρare specific internal energy,pressure,density and specific volume,respectively.Γ≡v(∂P/∂E)vis the Grüneisen parameter which is assumed to be given by the relationρΓ=ρ0Γ0,andEHandpHare specific internal energy and pressure under the Hugoniot shock state,respectively.In order to calculatepH,the quadratic Hugoniot relation between the shock velocityUsand the particle velocityUpis adopted as

whereS1andS2are material constants andC0is the initial bulk sound speed.Equation(A2)and the conservation laws of the mass,momentum and energy at the shockwave are combined to get

whereη≡(v0−v)/v0is the volumetric strain.
Shockwave
In coordinates moving at the penetration velocityU,the flow field near the rod/target interface is schematically shown in Fig.1.The subscripts r and t represent the rod and target,respectively.The subscripts 0,1,and 2 represent the states before the shockwave,after the shockwave and at the stagnation point(i.e.,rod/target interface),respectively.LetWdenote the flow velocity at any point along the central streamline toward the stagnation point.The boundary conditions are If the flow in rod or target toward its stagnation point is supersonic(W0>C0),then a shockwave will stand at some distance from the stagnation point.The conditions across the shockwave are represented by the Rankine-Hugoniot equations,


The relation of the shock velocity-particle velocity Eq.(A2),Us=W0,andUp=W0−W1are combined to get

By substituting Eq.(A10)into Eqs.(A7)–(A9),the remaining properties behind the shockwave are given by

Is entropic process from the shockwave to the stagnation point
The compressible Bernoulli equation along the isentropic process from the shockwave to the stagnation point is

It takes account of the internal energy and uses the real density of compressed material in the compressible Bernoulli equation,while the internal energy is not considered,and the initial density is used in the incompressible Bernoulli equation.The internal energy is related by the isentropic relation

In the integral,the material satisfies the EOS.Equations(A1)and(A3)are combined to get

Equation(A16),the isentropic condition(dE=−pdv)andρΓ=constant are combined to get

The relationp(v)between the pressure and the specific volume along the isentropic process from the shockwave to the stagnation point can be derived by integrating Eq.(A18).Substituting the relationp(v)into the Bernoulli equation and recalling thatW2=0 at the stagnation point leads to

Then the specificvolumev2at the stagnation point is obtained by solving Eq.(A19)and substituting it intop(v)to get the pressurep2.At last the internal energyE2can be derived from the EOS.
Up to now,if the initial state 0 is known,the above theory can be used to get every physical property at the stagnation point when the shockwave exists.If there is no shockwave,Eqs.(A7)–(A9)are not used,and Eqs.(A18)and(A19)are applied instead by setting the starting point as state 0 to get the property at the stagnation point.
Numerical solution
Equation(A18)is too complex to obtain the analytical solution,and it has to be integrated numerically.In the integration,the numerical format of Eq.(A18)from the(i−1)-th step to thei-th step is

Rearranging it gets

The integration is repeated in the direction of decreasing specific volume and ends at the stagnation point2 whereW2=0.The compressible Bernoulli equation Eqs.(A14)and(A16)are combined to get

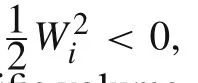
A last condition requires pressure equilibrium across the rod/target interface,p2r=p2t.Equations(A9),(A14),andW2=0 are combined to get

SubstitutingW0r=V−UandW0t=Uinto Eq.(A24)and further substituting the results into pressure equilibrium,p2r=p2t,yield
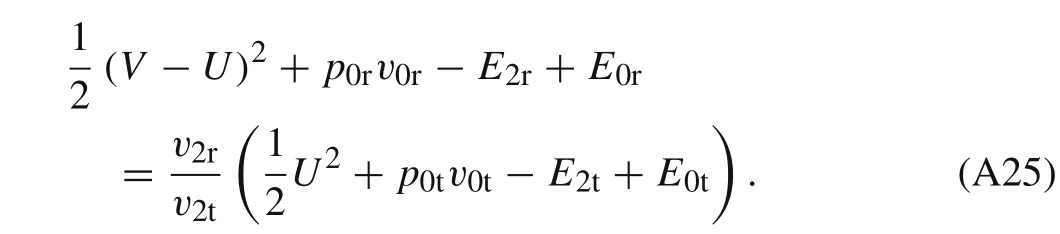

Equation(A26)can be rewritten as

Equations(4)and(A27)and the definition ofPEhare combined to get
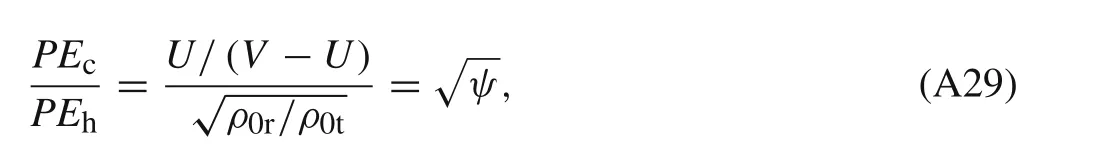
wherePEcis the penetration efficiency predicted by the compressible model.The larger value ofψmeans the higher the penetration efficiency predicted by the compressible model.Based on the supposed initial state 0,every physical property of the rod and target at the stagnation point can be obtained and then one gets the value ofψin Eq.(A27).The updated penetration velocity is

LetU=Unewand repeat the above process until convergence.
1.Birkhoff,G.,MacDougall,D.P.,Pugh,E.M.,etal.:Explosives with lined cavities.J.Appl.Phys.19,563–582(1948)
2.Hill,R.,Mott,N.F.,Pack,D.C.,et al.:Theoretical Research Report No.2/44,Jan.1944 and 13/44,Mar.1944.UK Armament Research Department
3.Eichelberger,R.J.:Experimental test of the theory of penetration by metallic jets.J.Appl.Phys.27,63–68(1956)
4.Alekseevskii,V.P.:Penetration of a rod into target at high velocity.Combust.Explos.Shock Waves2,63–66(1956)
5.Tate,A.:A theory for the deceleration of long rods after impact.J.Mech.Phys.Solids15,387–399(1967)
6.Tate,A.:Further results in the theory of long rod penetration.J.Mech.Phys.Solids17,141–50(1969)
7.Haugstad,B.S.,Dullum,O.S.:Finite compressibility in shaped charge jet and long rod penetration—the effect of shocks.J.Appl.Phys.52,5066–5071(1981)
8.Flis,W.J.,Chou,P.C.:Penetration of compressible materials by shaped-charge jets.In:Proceedings of 7th International Symposium on Ballistics,The Hague,The Netherlands,April(1983)
9.Backofen,J.E.:Supersonic compressible modeling for shaped charge jets.In:Proceedings of 11th International Symposium on Ballistics,Brussels,Belgium,May(1989)
10.Federov,S.V.,Bayanova,Y.M.:Hydrodynamic model for penetration of extended projectiles with consideration of material compressibility.In:Proceedings of 25th International Symposium on Ballistics,Beijing,China,May(2010)
11.Osipenko,K.Y.,Simonov,I.V.:On the jet collision:general model and reduction to the Mie–Grüneisen state equation.Mech.Solids 44,639–648(2009)
12.Flis,W.J.:A model of compressible jet penetration.In:Proceedings of 26th International Symposium on Ballistics,Miami,FL,September 12–16(2011)
13.Flis,W.J.:A jet penetration model incorporating effects of compressibility and target strength.Proc.Eng.58,204–213(2013)
14.Flis,W.J.:A simplified approximate model of compressible jet penetration.In:Proceedings of 27th International Symposium on Ballistics,Freiburg,Germany,April(2013)
15.Liu,M.B.,Liu,G.R.,Lam,K.Y.,et al.:Meshfree particle simulation of the detonation process for high explosives in shaped charge unlined cavity configurations.Shock Waves 12,509–520(2003)
16.Walker,J.D.,Grosch,D.J.,Mullin,S.A.:Ahypervelocity fragment launcher based on an inhibited shaped charge.Int.J.Impact Eng.14,763–774(1993)
17.Walters,W.P.,Scheffler,D.R.:A method to increase the tip velocity of a shaped charge jet.In:Proceedings of 23rd International Symposium on Ballistics,Tarragona,Spain,April(2007)
18.Corbett,B.M.:Numerical simulations of target hole diameters for hypervelocity impacts into elevated and room temperature bumpers.Int.J.Impact Eng.33,431–440(2006)
19.Steinberg,D.J.:Equation of state and strength properties of selected materials.Technical Report UCRL-MA-106439,Lawrence Livermore National Laboratory(1991)
20.Orphal,D.L.,Anderson,C.E.:The dependence of penetration velocity on impactvelocity.Int.J.ImpactEng.33,546–554(2006)
21.Tate,A.:Long rod penetration models—part II.Extensions to the hydrodynamic theory of penetration.Int.J.Eng.Sci.28,599–612(1986)
22.Rosenberg,Z.,Marmor,E.,Mayseless,M.:On the hydrodynamic theory of long-rod penetration.Int.J.Impact Eng.10,483–486(1990)
23.Anderson,C.E.,Walker,J.D.:An examination of long-rod penetration.Int.J.Impact Eng.11,481–501(1991)
24.Anderson,C.E.,Little field,D.L.,Walker,J.D.:Long-rod penetration,targetresistance,and hypervelocity impact.Int.J.ImpactEng.14,1–12(1993)
25.Rosenberg,Z.,Dekel,E.:A critical examination of the modified Bernoulli equation using two-dimensional simulations of long rod penetration.Int.J.Impact Eng.15,125–129(1994)
- Acta Mechanica Sinica的其它文章
- Amplitude modulation and extreme events in turbulent channel flow
- The influence of surface roughness on cloud cavitation flow around hydrofoils
- The influence of sub-grid scale motions on particle collision in homogeneous isotropic turbulence
- A simple algorithm to improve the performance of the WENO scheme on non-uniform grids
- Third-order polynomial model for analyzing stickup state laminated structure in flexible electronics
- A semi-analytical solution for electric double layers near an elliptical cylinder

