基于Matlab的级联型IIR滤波器设计与FPGA实现

黄玉健，黄永庆

(1.2.梧州学院 图像处理与智能信息系统广西高校重点实验室，广西 梧州 543002)

0 引言

IIR数字滤波器，即无限脉冲响应(Infinite Impulse Response，IIR)数字滤波器是最常用的数字滤波器之一。由于IIR滤波器具有通常阶数比较低长度比较短就可以实现所需功能且能以比较高的速度运行以及可以闭环设计算法等优点，它被广泛应用于数字信号处理(DSP)系统。在非实时系统和低速系统中，IIR滤波处理可以用软件算法实现，但是在实时高速处理系统中，用软件算法实现IIR滤波器功能往往无法满足要求。这时就必须要用硬件高速实现，而FPGA作为并行高速处理器件，不仅在运算处理速度上满足要求，而且集成度高、设计灵活、稳定性高，是实时性要求高或计算量大的系统的优秀解决方案。本文论述用Matlab设计IIR级联型数字滤波器并在FPGA上实现。

本文的组织结构如下：第2节对IIR直接型和级联型滤波器原理进行理论分析；第3节阐述用Matlab设计并求取级联型IIR滤波器系数；第4节阐述如何应用已经设计出的级联型IIR滤波器系数在FPGA实现滤波功能，通过联合Modelsim仿真和实际下载到FPGA芯片上运行来验证设计的正确性。第5节对本文进行总结。

1 IIR滤波器原理[1-2]

1.1 IIR滤波器基本原理

IIR滤波器全称为无限脉冲响应滤波器，它的单位脉冲响应是无限长的，它的离散变换的传递函数如公式(1)所示：

(1)

公式(1)中，M是分子的阶数，N是分母的阶数，al是分母的系数，bi是分子的系数，通常N>M。把公式(1)变换成差分方程，可以得到公式(2)：

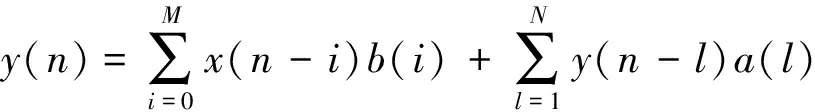
(2)

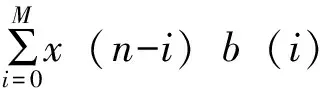
1.2 IIR滤波器的直接型结构形式

从公式(2)可以得到IIR滤波器的信号流图，结构形式如图1所示，称为IIR滤波器的直接Ⅰ型结构。

对于线性时不变系统的Z变换形式，交换子系统的次序，系统的函数不变。因此可以把公式(1)变换得到公式(3)：

(3)

根据公式(3)得到IIR滤波器的信号流图，结构如图2所示，称为IIR滤波器的直接Ⅰ型的变形。对于图(2)，由于两个串行时延支路具有相同的输入，因此可以合并，合并后得到下页图3，称为IIR滤波器直接Ⅱ型结构。对于N阶差分方程而言，相比直接Ⅰ型结构，直接Ⅱ型结构的延时单元少一半，仅需要N个延时单元。因此，直接Ⅱ型结构在用软件实现时可以节省存储空间，在用硬件实现时可以节省寄存器，比直接Ⅰ型结构有非常明显的优势。

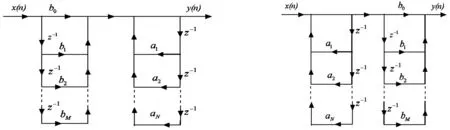
图1 IIR滤波器的直接Ⅰ型结构图 图2 IIR滤波器直接Ⅰ型结构的变形图

1.3 IIR滤波器的级联型结构形式

从公式(1)可知，一个N阶IIR滤波器系统可以用它的零点和极点表示。因为IIR滤波器系统函数的系数都是实数，所以它的零点和极点只能有两种情况：要么是实数，要么是复共轭对。把(1)式分子分母进行因式分解，可得公式(4)：

(4)

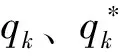
(5)

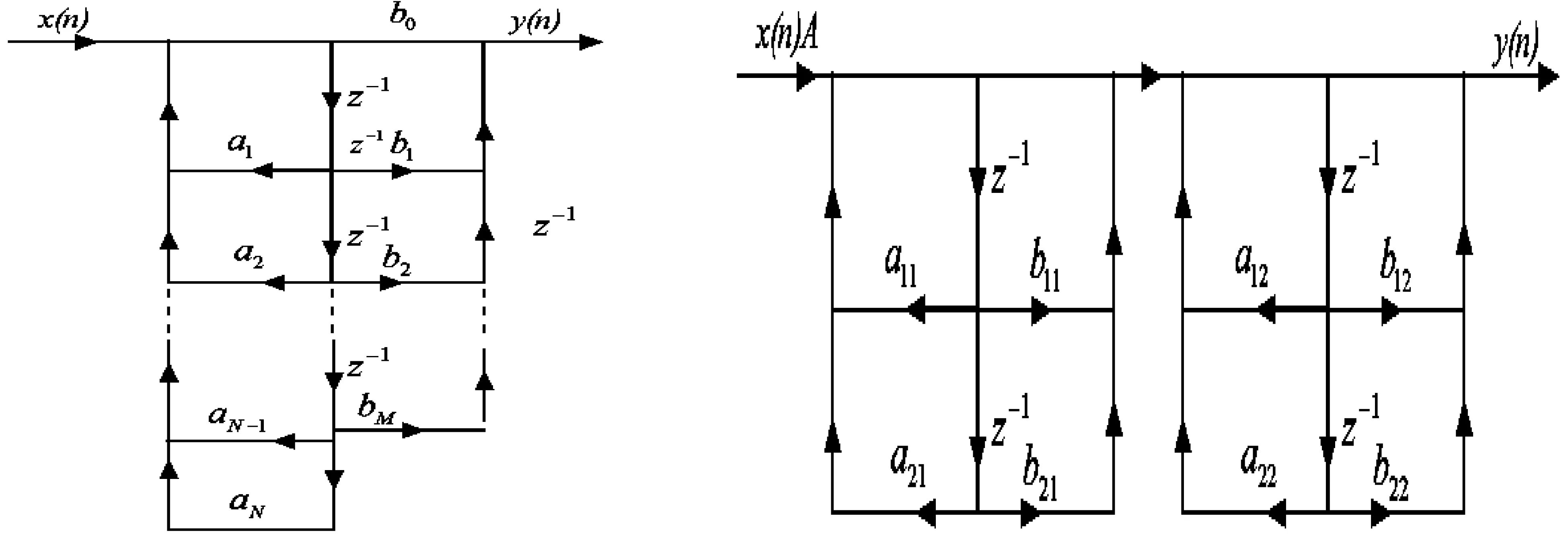
图3 IIR滤波器直接Ⅱ型结构图 图4 四阶IIR系统的级联结构图

2 IIR滤波器的设计及级联型结构系数生成[2]

2.1 用Matlab设计IIR滤波器

本论文设计一个六阶IIR低通以及一个六阶IIR高通滤波器。设计参数为：采样频率fs=10MHz，截止频率fc=3MHz，阻带衰减60dB，滤波器系数量化位数为14位。用Matlab调用cheby2函数设计满足参数要求的IIR滤波器，得到直接型IIR低通滤波器分母多项式系数a1=[1.0000 -1.0099 1.2239 -0.5394 0.2415 -0.0381 0.0047]和分子多项式的系数b1=[0.0269 0.0999 0.1948 0.2396 0.1948 0.0999 0.0269]；直接型IIR滤波器分母多项式系数a2=[1.0000 3.0736 4.3761 3.5128 1.6615 0.4334 0.0486]和分子多项式的系数b2=[0.0063 0.0066 0.0138 -0.0129 0.0138 0.0066 0.0063]。频率响应如下页图5所示。

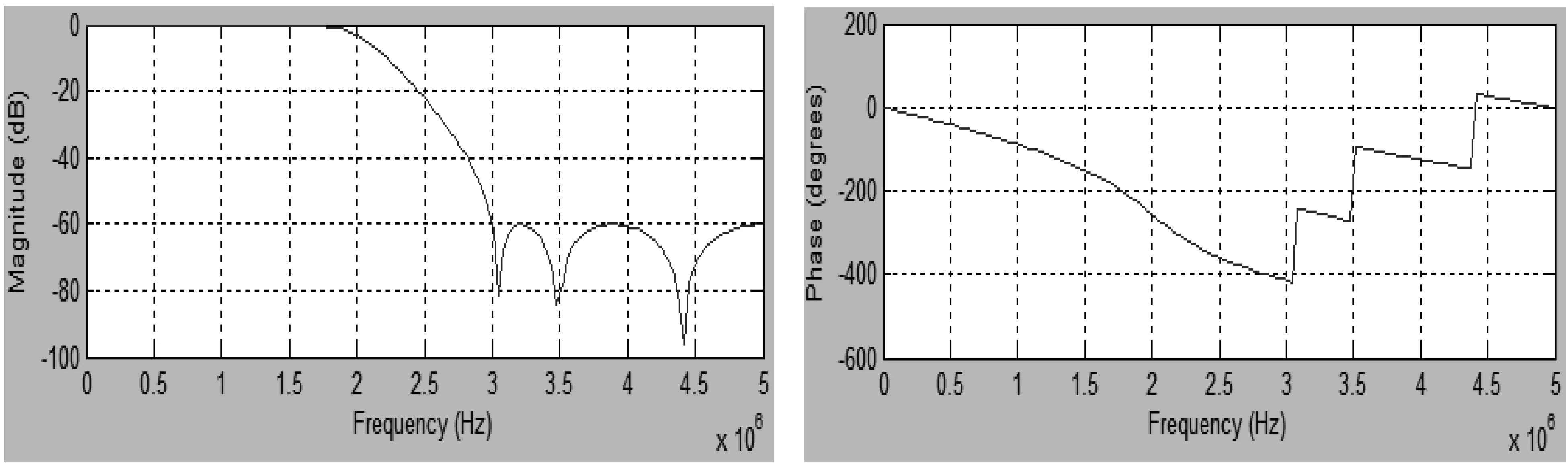
a.低通幅频响应 b.低通相频响应

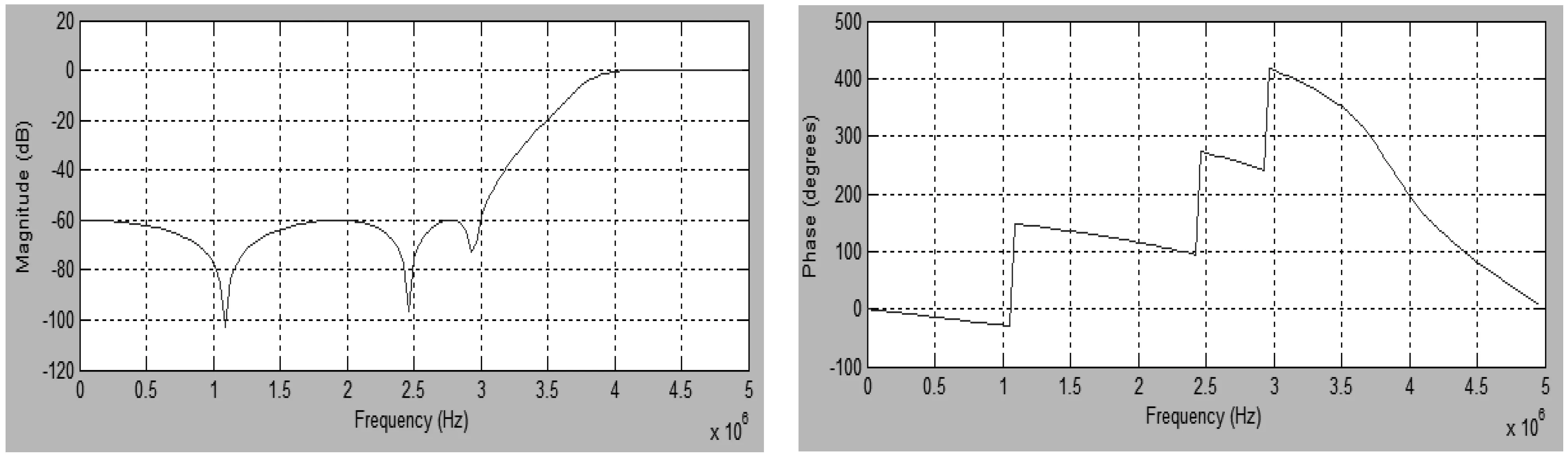
c.高通幅频响应 d.高通相频响应图5 六阶IIR滤波器频率响应图

2.2 级联型结构系数生成及量化

3 IIR滤波器在FPGA上实现及滤波测试

3.1 IIR滤波器在FPGA上实现

由上述可知，本设计的六阶IIR滤波器可用3个二阶IIR滤波器级联来实现，第3节已经对滤波器的系数进行了量化。根据级联结构量化系数可以得到低通滤波器的差分方程，见公式(6)；以及高通滤波器的差分方程，见公式(7)。

(6)

(7)

根据差分方程，可以得到二阶IIR滤波器的FPGA实现结构图[2]如下页图6所示。然后用3级二阶IIR滤波器级联得到六阶IIR滤波器。FPGA实现后的顶层RTL原理图如下页图7所示。

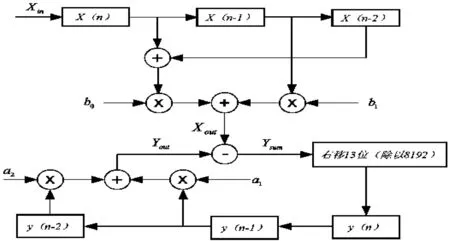
图6 二阶IIR滤波器的FPGA实现结构图

图7 六阶IIR滤波器FPGA实现顶层RTL电路图

3.2 仿真及下载测试

为了验证FPGA实现的IIR滤波器的滤波效果，对本设计分别采用Quartus II 联合Modelsim仿真验证和下载到FPGA器件Altera公司的Cyclone III 系列的EP3C25Q240C8芯片上实际运行滤波验证。IIR低通滤波Modelsim仿真图如8所示。图中Xin为输入频率1MHz正弦波和4.1MHz正弦波的叠加波形经14位量化后混合波形图，Y1out和Y2out分别是第一级和第二级滤波输出，Yout为最终滤波输出。下页图9则是IIR高通滤波Modelsim仿真图，输入波形参数同低通滤波输入波形参数一样。可以看出均达到良好滤波效果。

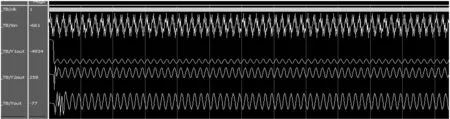
图8 IIR低通滤波器滤波效果Modelsim仿真图

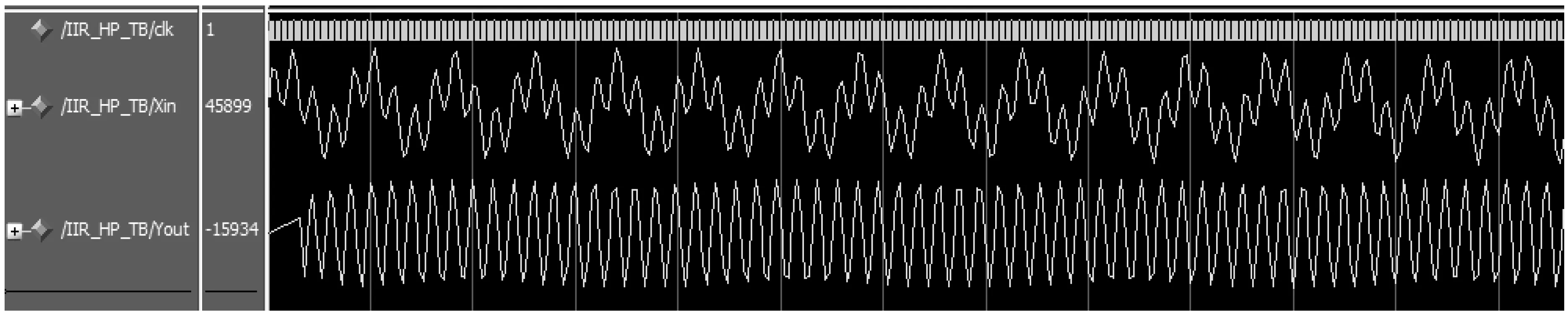
图9 IIR高通滤波器滤波效果Modelsim仿真图

下载到FPGA芯片运行实际低通滤波效果的SignalTap II图如图10所示。图10中Xin同样为输入频率1MHz正弦波和4.1MHz正弦波的叠加波形经14位量化并转换为HEX格式文件[5]，后经信号发生器产生的混合波形图[6]，IIR_OUT为滤波输出波形，同样可以看出滤波效果也很好。

图10 IIR低通滤波器实际运行滤波SignalTap II图

4 总结

本文用采用Matlab的切比雪夫II型函数设计出直接型IIR滤波器系数，然后再把直接型系数转换为级联型系数，最后采用Verilog语言在FPGA上实现。通过仿真验证与下载运行测试的结果表明，该设计是快速可靠的，可作为高速数字滤波器设计的较好方案。