基于最大类间方差的权重自适应活动轮廓模型

赵 怡，邓红霞，张 玲，李 钢

(太原理工大学 计算机科学与技术学院，山西 太原 030024)

0 引 言

活动轮廓模型自Kass等提出以来，便成为了图像分割领域内的研究热点[1]，其中Chan和Vese提出的基于图像全局信息的C-V模型是最为广为研究和应用的[2,3]，它可以较好地分割边缘对比度低的图像，演化曲线收敛速度快，对初始曲线的位置也不敏感，但在分割灰度不均匀的图像时，效果不理想。Li提出基于图像局部信息的局部二值拟合模型(local binary fitting，LBF)模型，克服了C-V模型分割灰度不均匀图像的不足[4]，但其算法复杂度较高，对初始位置敏感，同时易陷入局部极小值。针对LBF模型计算复杂度高的问题，Zhang等提出了局部图像拟合(local image fitting，LIF)模型，有效减小了运算量，同时保持了对灰度不均匀图像和噪声图像的分割精度[5]，但仍然存在对初始轮廓敏感和误分割问题。为了全面地考虑图像的灰度信息获得更优的分割结果，融合图像全局信息和局部信息的模型被相继提出[6,7]，比较著名的是LGIF模型[8]，但是LGIF不能自动选择权重参数。在实现时，通常都是人为设定的粗略参数，需耗费大量的时间和精力调整，且没有量化的选取标准。在曲线演化过程中，也不能根据图像的灰度情况进行实时调整，而权重参数的选择会直接影响演化曲线的分割速度和准确率。

针对以上问题，本文提出一种基于最大类间方差的权重参数自动调节模型。首先将最大类间方差的思想引入传统LIF模型，综合考虑目标和背景两类间的差异来有效减少误分割，提高了分割准确度。并将改进的模型作为局部项与C-V模型结合，降低对初始轮廓的敏感度，在权值参数的调节下共同促进曲线演化。对于权重参数的选择，本文引入了图像熵来实时获取图像分割过程中的灰度分布情况，自适应地为能量函数中的权值参数赋值。相比传统的实验经验选择法，本文选择了一种更加量化和合理的方式给权重赋值，有效提高了分割效率和准确度。实验结果表明，本文模型对于不同类型的灰度不均匀和噪声图像，都能够快速地完成分割，且精度和稳定性较高，对初始轮廓的位置也不敏感。

1 相关背景

1.1 图像局部熵

信息熵的理论自Shannon提出来以后，被广泛应用于图像处理领域。图像熵可以表示图像灰度的分布特征，描述图像的灰度均匀程度。

在图像分割中的任意时刻，演化曲线将图像分割为内外两部分区域，即inside(C)和outside(C)两部分。本文算法在每次迭代中获取演化曲线的位置，并计算曲线内部区域的图像局部熵Ein

(1)

其中，N表示图像的灰度级，pi表示第i级灰度出现的概率[9]，根据熵函数的极值性，当系统各元素概率均等时，熵函数取得最大值。由于分割曲线内部图像灰度的取值范围为[0,255]，当每一级灰度出现的概率相等时，熵函数取得最大值，由此计算得出图像局部熵函数的值域为[0,8]。

根据Shannon信息熵理论，当系统中事件的发生概率均等时，熵值最大。如果将这一理论推广到图像领域，那么当图像灰度均匀分布时，熵值较大，反之熵值较小。因此图像熵可以有效地衡量图像的灰度分布情况，适合作为权重参数来调节全局项与局部项的比重。

1.2 C-V模型

为简化Mumford-Shah模型，Chan和Vese于2001年提出了基于图像全局信息的C-V模型，其核心思想是把图像中的目标和背景考虑成两个简单的两类问题，利用简单的二聚类思想控制曲线朝目标边界演化，从而划分图像的目标和背景。

对于要分割的图像I，图像域为Ω，假定图像是由灰度均匀分布的目标和背景(c1和c2)两个部分组成，其能量泛函定义如下

(2)

其中，λ1和λ2为非负常量，一般取λ1=λ2=1。C表示图像域内的闭合演化曲线。在任意时刻，图像I被演化曲线C划分为目标和背景两个区域，即inside(C)和outside(C)两部分，c1和c2分别是目标和背景区域的平均灰度值。

将水平集函数嵌入式(2)得到式(3)

(3)

并最小化能量泛函，得到对应的梯度下降流

(4)

其中

(5)

(6)

Hε(φ)和δε(φ)分别为Heaviside函数和它的一阶导Dirac函数

(7)

(8)

C-V模型可以得到全局最优分割，避免陷入局部极小值，且演化时曲线收敛速度快，对初始轮廓的位置也不敏感。但由于其没有考虑到图像局部灰度特征的变化，在分割噪声图像和灰度不均匀图像时表现较差。

1.3 LIF模型

Zhang等提出了局部图像拟合模型LIF，该模型提出了一个新的局部能量拟合项来逼近原始图像灰度值。

首先，利用分片光滑函数来近似拟合待分割图像，该局部拟合函数LFI定义为

ILFI=m1Hε(φ)+m2(1-Hε(φ))

(9)

其中，m1和m2定义如下

m1=mean(I∈({x∈Ω|φ(x)<0}∩Wk(x)))

(10)

m2=mean(I∈({x∈Ω|φ(x)>0}∩Wk(x)))

(11)

此外，Wk是矩形窗口函数，一般取为高斯窗口或常数窗口，本文采用标准的高斯窗口Kσ(x)，尺寸为(4k+1)×(4k+1)，标准差σ为尺寸参数，用于调节窗口尺寸大小，k为小于σ的最大整数。

通过最小化原始图像与拟合图像的差异，得到LIF模型总的能量泛函如下

(12)

LIF模型有效地利用了图像的局部信息，较好地克服了噪声和灰度不均匀时的分割问题。但是由于其没有利用图像的全局信息，容易陷入局部极小值。此外，在处理一些复杂的灰度不均匀图像时还是存在一定的局限性，会出现误分割现象。

2 本文模型

最大类间方差法可以有效衡量两类间的离散度。对于图像分割来说，目标和背景的类间差异越大，说明分割的结果越准确。当目标被误分割为背景时或者背景被误分割为目标时，都会使类间方差减小。因此使类间方差最大化，可以有效地减少图像的误分割现象[10]。受这一思想的启发，本文将最大类间方差引入LIF模型，提出基于最大类间方差的局部拟合模型(maximum classes square error local image fitting，MCSELIF)，综合考虑目标和背景两类间的差异来减少误分割，提高分割准确度。

根据最大类间方差的计算思想[11]，两类均值m1和m2的类间方差为

(13)

其中，ω1和w2分别表示图像内属于m1的部分和m2的部分占整个图像的比值。当演化曲线嵌入水平集函数后有

(14)

(15)

根据式(14)和式(15)以及Heaviside函数的性质，图像中属于m1的部分所占的比值是Hε(φ(x))，属于m2的部分所占的比值是(1-Hε(φ(x)))，于是表示m1和m2占比的ω1和ω2表示为

ω1=Hε(φ(x))

(16)

ω2=1-Hε(φ(x))

(17)

显然有ω1+ω2=1。

m0表示图像的平均灰度值，有

m0=ω1m1+ω2m2

(18)

将式(18)代入式(13)化简可得类间方差项

(19)

将类间方差项加入LIF模型得到最大类间方差的改进MCSELIF模型的能量泛函为

(20)

将改进后的MCSELIF模型和C-V模型分别作为局部能量项和全局能量项，共同驱动曲线向目标边缘演化，同时，本文基于图像熵可以有效反应灰度信息的思想，通过实时计算图像熵来为权重赋值。因此，权重参数可以实时地利用图像熵来获取图像的灰度分布情况，从而自适应地调节全局项和局部项的比重。在每一次迭代中，权重参数都会根据图像的具体情况进行调整。当图像灰度值均匀分布时，图像熵值较大，由全局项主导轮廓曲线的演化；当图像强度分布不均匀时，图像熵值较小，由局部数据能量拟合项主导轮廓曲线的演化，能量泛函定义如下

E(φ,c1,c2,m1,m2)=(1-ω)EM_LIF+ωECV

(21)

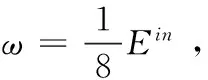
对于大部分图像来说，灰度不均匀的情况较严重，为了获得更加准确的分割结果，对于这类图像，本文在局部熵的基础上加入了微调参数∂(0≤∂≤1)，通过降低ω的值，来削弱全局拟合力的作用，这也说明了本文模型在处理不同种类图像时更具适用性。即

(22)

在曲线演化过程中，水平集函数可能会偏离符号距离函数，造成曲线演化不稳定，这时就需要周期性的将水平集函数初始化为符号距离函数。为了解决这一问题，加入在曲线演化过程中能自动维持水平集函数符号距离性质的正则项

(23)

此外，为了保证演化曲线尽可能短而平滑，避免小的孤立点引起的局部极小值出现，加入长度惩罚项

(24)

本文模型的最终能量泛函为

E(φ,c1,c2,m1,m2)=(1-ω)EM_LIF+ωECV+
vL(φ)+μP(φ)

(25)

根据标准梯度下降流[12]，得到关于水平集演化的表达式如下

(26)

其中，FM_LIF和FCV分别为局部拟合力和全局拟合力

(27)

FCV=ω[-λ1(I-c1)2+λ2(I-c2)2]

(28)

3 实验结果与分析

本文选取了不同种类的图片进行分割来体现本文模型具有的广泛适用性，同时通过多组对比实验来证明本文模型的优越性：①对初始轮廓曲线的位置不敏感；②分割精度高；③运算时间和迭代次数降低；④自适应地调节权重参数。

本文的实验平台是MATLABR2016a，Microsoftwindows10 64位操作系统，CPUi7 4790，内存8GB。实验参数如无特殊说明选择如下：σ=3，λ1=λ2=1，ν=0.003×255×255，时间步长为0.02。

此外，本文模型的微调参数如无特殊说明选取∂=1，LGIF模型的权重参数ω选取分割结果最优时的数值。

3.1 对眼底视网膜血管的分割

由于视网膜血管的结构复杂，数量庞大且微小，加之血管本身存在灰度不均匀性且血管边界的轮廓模糊，导致传统模型无法对此类图像进行正确的分割。其中，视盘内血管由于受灰度不均匀影响最大，一直是视网膜血管分割中的难点。本文的视网膜图像数据自STARE国际数据库中的眼底视网膜血管彩色图像，且选用噪声低和血管对比度高的绿色通道图像[13]。本文对视网膜血管选取的分割区域均为(343×343)大小的图片。该组实验结果表明本文模型能够克服噪声和灰度不均匀的影响，快速准确地完成对结构复杂的眼底视网膜血管的分割。

图1为不同模型对视网膜血管的分割，文本选取了视网膜血管图像中比较有代表性的区域，标识在图1(a)～图1(d)中，其中图1(c)和图1(d)为视盘内血管。由于视网膜血管的灰度不均匀现象较严重且细微组织较多，本组实验选择来提高局部项的比重获得更细致的分割。LGIF模型的权重参数选择如下：ω=0.06，ω=0.5，ω=0.0001，ω=0.0005。图1分割结果表明：对于图1(e)，LIF模型出现了较大面积的多余曲线；LGIF模型由于受右上角视盘干扰较大，造成分割失败。对于图1(f)，本文模型相比LIF模型可以分割出更多的细微血管；LGIF模型在右上角出现了误分割。

对于图1(g)和图1(h)，由于图视盘内血管受灰度不均匀干扰较大，LIF模型和LGIF模型都不能完成正确分割。本文模型对于这类背景很不均匀的复杂图像，能有效利用类间差异项，减少误分割，同时能够实时获取当前的灰度信息，及时调整权重参数得到准确地分割结果。LIF在分割血管时陷入局部极小值，造成血管分割不足和误分割；LGIF因不能自适应地调节全局项和局部项的比重，造成血管分割结果不理想。

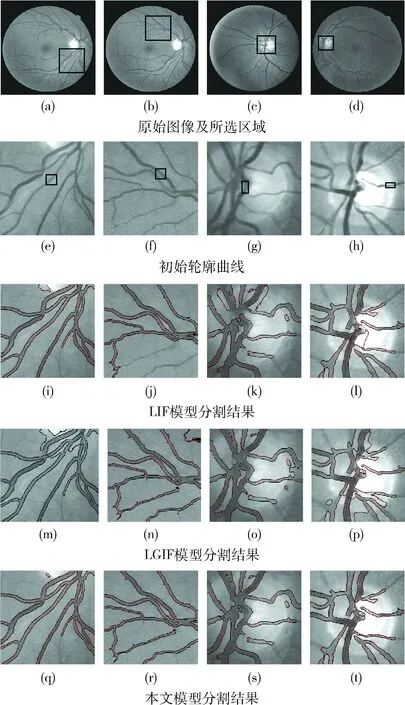
图1 不同模型对视网膜血管图像的分割

表1为3种不同模型分割视网血管图像的迭代次数和运行时间。由表中的数据可知迭代次数和运算时间：LIF模型>LGIF模型>本文模型。可见本文模型结合类间差异项增强演化动力，通过权重参数的自适应调节，选择最恰当的参数优化算法，实现了局部项和全局项的比重均衡，提高了分割效率。

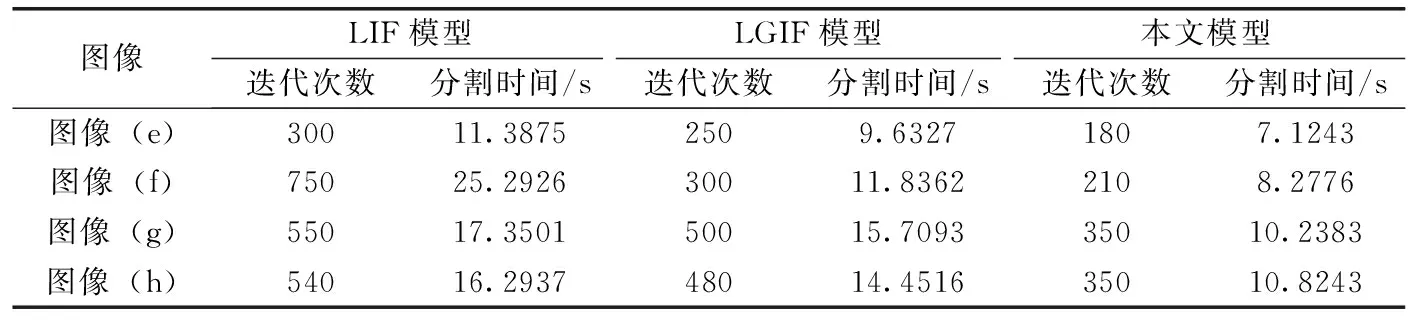
表1 不同模型分割的迭代次数和运行时间对比

3.2 对初始轮廓的敏感度对比

本文设置了两组对比实验来验证本文模型对初始轮廓的鲁棒性，分别如图2、图3所示。图2使用一副灰度分布不均匀人工合成图像(434×329)，来验证不同模型对不同位置和大小的初始轮廓曲线的敏感程度，本组实验选择长度项参数：ν=0.007×255×255，LGIF模型权重参数的选择分别为：ω=0.001。分割结果表明：LIF模型均不能完成图像分割，LGIF模型只有在最后一种情况下才能完成图像分割,而本文模型的轮廓曲线初始化位置,无论在下面3种中的哪一种情况下，均可完成图像分割。

图2 不同初始轮廓位置下的分割

图3 本文模型对两幅图片在不同初始轮廓曲线下的分割注：其中黑色矩形框为初始轮廓曲线，白色为最终分割结果。

第二组对比实验为本文模型对两幅灰度不均匀和噪声图片在不同位置和大小的初始轮廓曲线下的分割结果，如图3所示。实验结果表明本文模型不受初始轮廓曲线位置和大小的影响，均可以取得正确的分割，充分验证了本文模型对初始轮廓曲线不敏感。

3.3 对其它噪声和灰度不均匀图像的分割

为了验证本文模型对其它噪声和灰度不均匀图像分割的优越性，本文对星云图(374×343)，超声波图(349×343)和二值图(352×343)，机场图(434×174)进行了分割实验，图4为不同模型的分割结果。图4(a)的参数设定为：σ=8,ν=0.007×255×255，时间步长为0.001。图4(b)的参数设定：σ=8，ν=0.7×255×255，时间步长为0.0003。图4(c)的参数设定：ν=0.007×255×255。LGIF模型权重参数的选择分别为：ω=0.06，ω=0.5，ω=0.5，ω=0.3。本文模型无需手动调节权重参数。

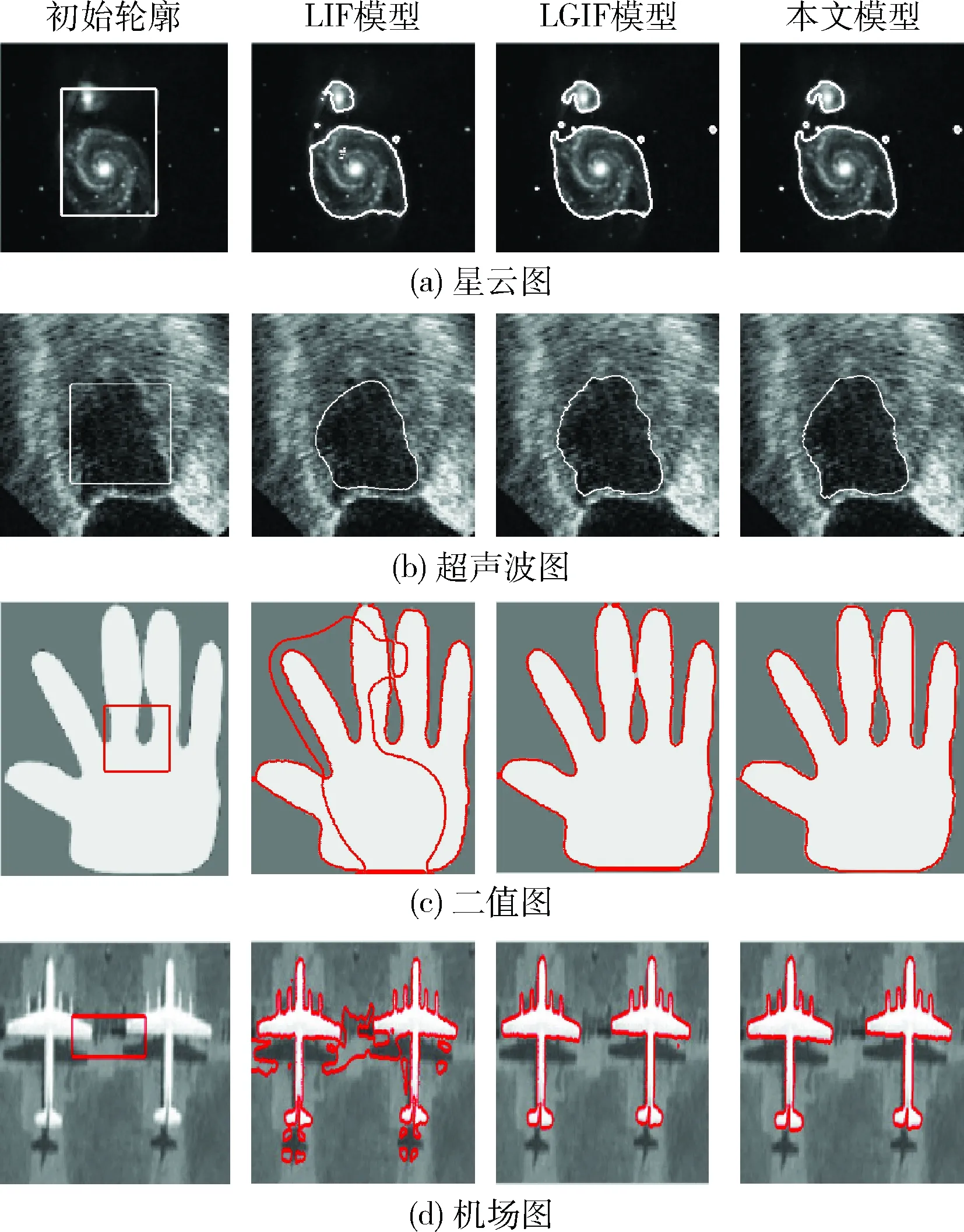
图4 不同模型对其它噪声和灰度不均匀图像的分割

3.3.1 分割结果的比较

由图4中的分割结果可知：对于图4(a)，3种模型分割结果相近。对于图4(b)，本文模型能够完整地对图像进行分割，而LGIF模型和LIF模型在边缘部分过度分割，丢失了部分图像信息。对于图4(c)，只有本文模型能够分割出指间相连的部分，体现出本文模型具有更高的分割精度。对于图4(d)，LIF模型分割失败，LGIF模型虽可以完成分割，但与本文模型分割结果相比出现了轻微噪点。

3.3.2 迭代次数和运算时间比较

表2为3种模型分别完成图4中4幅不同图像分割的迭代时间和运行时间对比，分析表中的数据可知，本文模型所需的迭代次数最少和时间开销最低。本文模型利用图像熵的自动调节能力为全局项和局部项实时选取最优的权重，有效减少了水平集演化的迭代次数和时间，同时利用类间差异项增强曲线演化动力，加快了收敛速度。

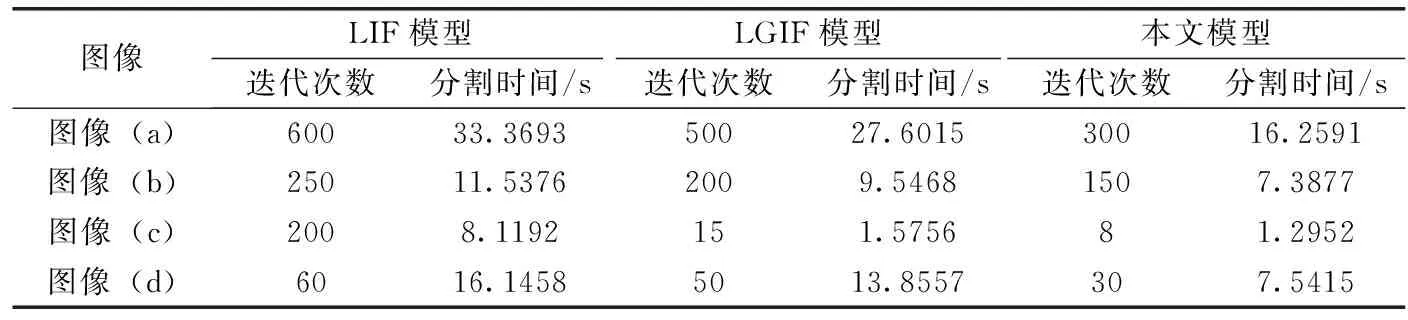
表2 不同模型分割的迭代时间和运行时间对比

4 结束语

本文提出了一种基于最大类间方差的权重参数自动调节模型。首先在LIF模型中加入最大类间方差项来有效减少误分割，提高分割准确率，增强曲线演化的动力；然后将改进的模型作为局部项与C-V模型结合，利用图像的局部信息和全局信息共同驱动曲线演化，降低对初始轮廓的敏感度；同时采用了一种量化的权重参数自适应方法来调节能量泛函中全局项和局部项的比重，该方法通过计算图像熵值判断图像的灰度分布情况，在每一次迭代中实时更新权重参数。相比传统的实验经验选择法，本文模型能够更好地平衡全局项与局部项的比重。

本文通过多组实验验证了本文模型相对于其它模型在处理多种类型的噪声和灰度不均匀图像时的优越性，不仅对轮廓曲线的初始化位置具有低敏感性，而且提高了分割精度，并有效降低了运算时间、迭代次数。

[1]Liu Weigping,Shang Yanfeng,Yang Xin.Active contour model driven by local histogram fitting energy[J].Pattern Recognition Letters,2013,34(6):655-662.

[2]Wang Xiaofeng,Min Hai,Zhang Yigang.Multi-scale local region based level set method for image segmentation in the pre-sence of intensity inhomogeneity[J].Neurocomputing,2015,151(3):1086-1098.

[3]Zheng Qiang,Dong Enqing,Cao Zhulou,et al.Active contour model driven by linear speed function for local segmentation with robust initialization and applications in MR brain images[J].Signal Processing,2014,97(7):117-133.

[4]Liu Shigang,Peng Yali.A local region-based Chan-Vese model for image segmentation[J].Pattern Recognition,2012,45(7):2769-2779.

[5]Yuan Jianjun,Wang Jianjun,Liu Lipei.Active contours dri-ven by local intensity and local gradient fitting energies[J].International Journal of Pattern Recognition & Artificial Intelligence,2014,28(3):1455006.

[6]Zhao Yuqian,Wang Xiaofang,Frank Y Shih,et al.A level-set method based on global and local regions for image segmentation[J].Pattern Recognition and Artificial Intelligence,2012,26(1):1-14.

[7]QI Shile,WANG Meiqing.“Two-stage” active contour model driven by local and global information[J].Journal of Image and Graphics,2014,19(3):421-427(in Chinese).[戚世乐,王美清.结合全局和局部信息的“两阶段”活动轮廓模型[J].中国图象图形学报,2014,19(3):421-427.]

[8]Jiang Xiaoliang,Wu Xiaoliang,Xiong Ying,et al.Active contours driven by local and global intensity fitting energies based on local entropy[J].Optik-International Journal for Light and Electron Optics,2015,126(24):5672-5677.

[9]He Chuanjiang,Wang Yan,Chen Qiang.Active contours driven by weighted region-scalable fitting energy based on local entropy[J].Signal Processing,2012,92(2):587-600.

[10]ZHANG Qin.Research of image segmentation based on improved CV model[D].Jinan:Shandong Normal University,2013(in Chinese).[张芹.基于改进CV模型的图像分割技术研究[D].济南:山东师范大学,2013.]

[11]Song Yu,Wu Yiquan,Dai Yimian.A new active contour remote sensing river image segmentation algorithm inspired from the cross entropy[J].Digital Signal Processing,2016,48(C):322-332.

[12]YUAN Ye.Image segmentation technology based on partial differential equation[D].Chongqing:Chongqing University,2012(in Chinese).[原野.偏微分方程图像分割模型研究[D].重庆:重庆大学,2012.]

[13]Zhao Yitian,Rada Lavdie,Chen Ke,et al.Automated vessel segmentation using infinite perimeter active contour model with hybrid region information with application to retinal images[J].IEEE Transactions on Medical Imaging,2015,34(9):1797-1807.