基于度值标准差的复杂网络可靠性
李 锴,何永锋
(1.装甲兵工程学院 技术保障工程系,北京 100072;2.装甲兵工程学院 基础部,北京 100072)
0 引 言
现阶段主要复杂网络模型[1,2]有随机网络模型、小世界网络模型和无标度网络模型。复杂网络通常作为复杂系统的抽象模型,包含大量网络节点,节点之间具备错综复杂的连接关系。复杂网络的可靠性和抗毁性问题一直受到广泛关注[3-5],研究复杂网络可靠性主要通过移除网络节点和连接边对网络效率及连通度的影响来体现,主要的理论判据有网络熵值和自然连通度[6-8]。本文基于复杂网络节点度值的标准差,提出网络可靠性函数的定义,证明网络可靠性函数的收敛性及单调性,研究随机网络和无标度网络在两种失效模式下的可靠性变化规律,验证网络可靠性函数的合理性及有效性。
1 复杂网络模型
复杂网络模型主要经历4个模型阶段:规则网络(regular network)、随机网络(random network)、小世界网络(small-world network)和无标度网络(scale-free network)。为研究复杂网络模型的拓扑结构,专家学者定义许多特征量,主要有度与度分布、平均距离,聚类系数、点(边)介数,谱半径、连通性、密度、网络效率和网络熵等[9]。例如度及度分布按照拓扑结构对网络进行分类,网络的熵描述了网络的随机程度。随机网络和无标度网络是两种典型网络模型,对于随机网络本身而言,节点对之间是否存在连接边是完全随机的,网络整体体现均匀的特性;无标度网络认为网络本身不是静态的,并且连接边的存在并非完全随机化,而是满足一定的演化规则,现在许多关键基础设施网络(如互联网、电力和铁路网络)均满足无标度特性[10]。
1.1 ER随机网络
随机网络模型是与规则网络模型完全对立的模型,Erdös和Rényi利用在节点对之间随机添加一定数量连接边的方式构造ER随机网络[1],该网络模型可以通过解析方法进行精确研究分析,当网络中的节点数N→+∞时,网络中节点的度值都集中在某个固定值附近,不会出现度值极大或极小的节点,网络整体表现出均匀性,ER随机网络模型的节点度分布服从泊松(poisson)分布
(1)
其中,λ为ER随机网络的平均度。
ER网络拓扑结构及其度分布的直方图(N=50,p=0.2),如图1所示。
1.2 BA无标度网络
Barabási等指出真实网络具备无标度的特殊性质[11],充分考虑复杂网络“增长”和“择优”的非随机动态特性,无标度网络中具有少量度值很高的Hub节点和大量低度值的节点,这种非均匀结构导致偏态度序列分布,具体表现为幂律的度分布特性
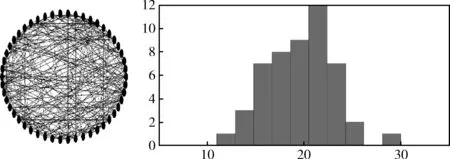
图1 ER网络拓扑结构及其度分布的直方图(N=50,p=0.2)
(2)
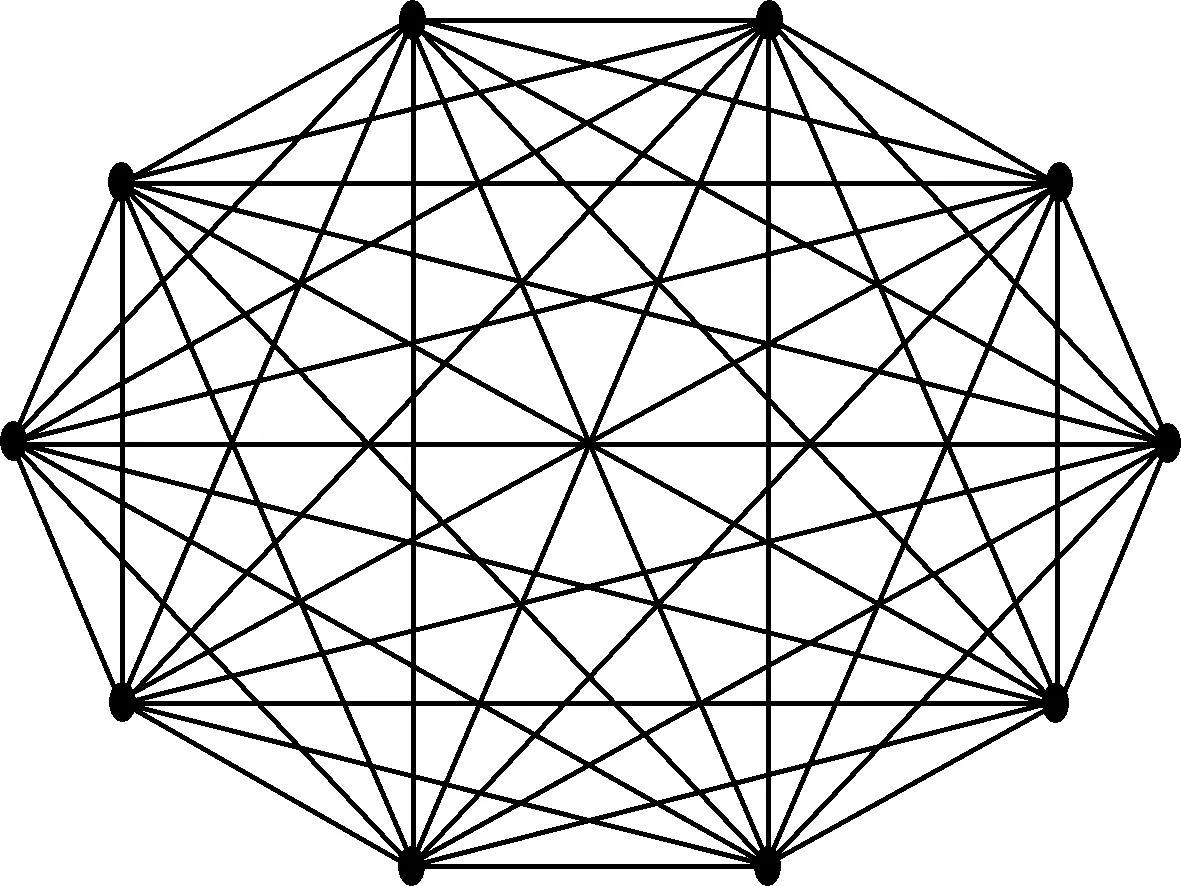
其中,α为系数,q为分布指数。通常情况下,真实网络的分布指数满足2 BA网络拓扑结构及其度分布的直方图(N=50,m=m0=3),如图2所示。 图2 BA网络拓扑结构及其度分布的直方图(N=50,m=m0=3) 表1为复杂网络模型的相关特性[9]。 表1 复杂网络模型的相关特性 复杂网络的可靠性是指网络在规定的条件下,在规定的时间内完成规定功能的能力[3]。复杂网络通常包含大量网络节点,节点具备异质性及复杂的连接关系,整个网络整体呈现多层次、多维数、多等级和多属性的复杂特性。对于无向网络而言,不考虑重边及自环等特殊情况,利用图论理论将复杂网络抽象为图G(V,E),其中V={v1,v2,…vN}为网络的节点集合,N为网络节点总数,E={e1,e2,…eM}为网络的边集合,M为网络边的总数,集合E满足E⊂V×V。网络节点通过边进行信息流、物质流和能量流的交换,网络节点及边的拓扑结构决定网络的连通性,删除或添加网络边对网络的连通性及网络功能产生重要影响。由于复杂网络的度及其度分布是网络拓扑结构的直接体现,因此本文基于节点度值的标准差σ来定义网络可靠性函数H(σ,N,M)。 本文对网络可靠性函数H(σ,N,M)作如下定义 (3) 依据可靠性定义,网络可靠性函数H(σ,N,M)满足以下两个性质: (1)收敛性:对于给定的任意节点总数N和边数M,0≤H(σ,N,M)≤1。 (2)单调性:对于给定的任意网络,任意删除1条边,网络可靠性H(σ,N,M)减小。 下面分别对两个性质进行证明: (1)对于网络可靠性函数H(σ,N,M)而言,函数为指数函数且满足 (4) 图3 全局耦合网络(N=10) 对于另外一种极端情况,网络中的节点数为N,边数M=0,整个网络中不存在连接边,称为孤立点网络,如图4所示。此时网络的度值标准差σ=0,计算得到网络可靠度为H(σ,N,M)=exp(-10)=4.54×10-5≈0。 图4 孤立点网络(N=10) 通过对两种情况分析,证明得到0≤H(σ,N,M)≤1,因此性质1成立。 本文采用逆推法,证明过程如下: 对不等式左侧σ′2进行计算 (5) 对不等式右侧(σ+N)2进行计算 (6) 若σ′2<(σ+N)2,需要满足 (7) (8) 由于dmax=N-1,因此 (9) 上式在N≥3时恒成立,即对于任意节点数N≥3的复杂网络,不等式σ′2<(σ+N)2恒成立,因此可靠性函数H(σ,N,M)满足性质2。 从本节分析中可以看出,以网络节点数N、网络边数M和网络度值标准差σ构造网络可靠性函数H(σ,N,M)能严格收敛于区间[0,1]中,孤立点网络和全局耦合网络分别对应Hmin=0和Hmax=1;网络可靠性函数H(σ,N,M)具备单调性,任意删除网络中的1条边,H(σ,N,M)严格递减,可以用H(σ,N,M)来度量复杂网络的网络可靠度,研究复杂网络的可靠性与拓扑结构的关系。 对于ER随机网络和BA无标度网络,采用两种失效方式逐步移除网络中的边:随机破坏和蓄意攻击。随机破坏是指没有固定目标,完全随机地按照一定比例地将边进行 移除;蓄意攻击是指按照一定策略,有针对性地对重要连接边进行移除。在两种模式下,网络中逐渐出现孤立节点,网络的连通性逐渐降低,当所有连接边被移除,网络则无法进行信息流、物质流和能量流的交换,从而无法完成网络规定的功能,此时认为网络可靠度为零[12,13]。 在蓄意攻击的失效模式下,本文采用边介数来表征连接边的重要度[14,15],边em的介数Bm定义为 (10) 边介数Bm描述了边em对网络中节点对之间信息传播的控制能力,若节点对ii′不存在路径或边em不存在最短路径中,则边em不具备对于节点对ii′信息传播的控制能力。通常情况下,节点对的最短路径存在多条,信息传播总是沿着其中的一条最短路径进行,边介数Bm则为信息通过边em的概率。 图5为两种失效模式下,ER随机网络和BA无标度网络可靠性函数H(σ,N,M)与连接边移除比例f的仿真结果,其中网络的节点数N=100,初始时刻网络的平均度λ=90。 图5 ER网络和BA网络可靠性函数与边移除比例的仿真结果 分析仿真结果可得到以下结论: (1)在两种失效模式下,网络可靠性随着边移除比例f增大而逐渐降低,并且可靠性函数H(σ,N,M)严格递减。随着边移除比例f逐渐增大,网络中的节点逐渐成为孤立节点,无法完成信息流、物质流和能量流的传输等功能,最终网络可靠度逐渐降低到零。 (2)在随机破坏的失效模式下,相对于ER随机网络而言,BA无标度网络整体表现出较强的可靠性,当f<0.5时,BA无标度网络的可靠性下降速度较慢,整体表现出较高的可靠性;ER随机网络面对随机破坏的失效模式,网络可靠性下降速率相对平稳,未出现较大波动。 (3)在蓄意攻击的失效模式下,BA无标度网络的可靠性速度下降非常迅速,在f=0.4附近时接近于零,体现出明显的脆弱性;ER随机网络的可靠性下降速度也比随机破坏下迅速,当f=0.8时基本接近于零。ER随机网络和BA无标度网络的可靠性在蓄意攻击模式下整体相对较低,说明蓄意攻击对网络可靠性影响较大。 在随机破坏的模式下,BA无标度网络表现出较高的可靠性,主要是由于BA无标度网络的度分布为幂律分布,表现出较强的非均匀性:网络中存在少量的Hub节点,度值相对很大,大部分节点的度值都相对很小,当移除比例f较小时,网络中的Hub节点仍然处于连通状态,网络的可靠度较高;当移除比例f逐渐增大时,Hub节点的度值也开始大量下降,直接体现为网络可靠性下降。由于这种非均匀性,Hub节点的连接边则成为蓄意攻击的目标,有意识地移除Hub点的连接边会对整个网络的连通度及可靠性产生很大影响。对于ER随机网络而言,其度分布为泊松分布,大部分节点的度值分布在λ附近,不会出现度值极大或极小的节点,网络体现出均匀性,在随机破坏和蓄意攻击两种模式下,ER随机网络的可靠性下降没有出现较大波动,相对均匀平稳。 由于ER随机网络是连接边完全随机化的随机均匀网络,而BA无标度网络是具备“增长”和“择优”特征的幂律非均匀网络,两者的网络拓扑结构具有完全不同的特征,本文从度值标准差σ来定义网络可靠性函数H(σ,N,M),证明函数具备收敛性和单调性,最后通过仿真方法分析在随机破坏与蓄意攻击的失效模式下,ER随机网络和BA无标度网络的可靠性变化特征,并对变化机理进行阐述分析,验证网络可靠性函数H(σ,N,M)的可行性和有效性。 [1]HEDaren,LIUZonghua,WANGBinghong.Complexsystemsandcomplexnetworks[M].Beijing:HigherEducationPress,2012:178-210 (inChinese).[何大韧,刘宗华,汪秉宏.复杂系统与复杂网络[M].北京:高等教育出版社,2012:178-210.] [2]SUNXijing,SIShoukui.Complexnetworkalgorithmsapplication[M].Beijing:NationalDefenseIndustryPress,2015:236-257(inChinese).[孙玺菁,司守奎.复杂网络算法与应用[M].北京:国防工业出版社,2015:236-257.] [3]TANYuejin,ZHAOJuan,WUJun,etal.Reviewonthenetworkreliabilitybasedonpaths[J].SystemsEngineering-Theory&Practice,2012,32(12):2724-2730(inChinese).[谭跃进,赵娟,吴俊,等.基于路径的网络可靠性综述研究[J].系统工程理论与实践,2012,32(12):2724-2730.] [4]HUANGNing,WUZhitao.Surveyofnetworkreliabilityeva-luationmodelsandalgorithms[J].SystemsEngineeringand Electronics,2013,35(12):2651-2660(inChinese).[黄宁,伍志韬.网络可靠性评估模型与算法综述[J].系统工程与电子技术,2013,35(12):2651-2660.] [5]JiangYN.Surveyonnetworkreliabilityevaluationmethods[J].ComputerScience,2012,39(5):9-13. [6]WuLS,TanQM,ZhangYH.Networkconnectivityentropyanditsapplicationonnetworkconnectivityreliability[J].PhysicaA,2013,392(2):5536-5541. [7]WULiusan,TANQingmei,ZHANGYuehui.Theimpactofnetworkarc’sgrowthonthenetworkreliability[J].ChineseJournalofManagementScience,2015,23(1):65-72(inChinese).[吴六三,谭清美,张跃辉.网络弧生长对网络可靠性的影响[J].中国管理科学,2015,23(1):65-72.] [8]LUOPeng,LIYongli,WUChong.Complexnetworksevolutionresearchwithusingthenetworkstructureentropy[J].ComplexSystemsandComplexityScience,2013,10(4):62-68(inChinese).[罗鹏,李永立,吴冲.利用网络结构熵研究复杂网络的演化规律[J].复杂系统与复杂性科学,2013,10(4):62-68.] [9]LIKai,WUWei.Researchstatusofweaponequipmentsystem-of-systemsbasedoncomplexnetwork[J].JournalofAcademyofForceEngineering,2016,30(4):7-13(inChinese).[李锴,吴纬.基于复杂网络的武器装备体系研究现状[J].装甲兵工程学院学报,2016,30(4):7-13.] [10]ZhangLM,LiDQ,FuB,etal.Reliabilityanalysisofinterdependentlattices[J].PhysicaA,2016,452(15):120-125. [11]ColmanER,RodgersGJ.Complexscale-freenetworkswithtunablepower-lawexponentandclustering[J].PhysicaA,2013,392(2):5501-5510. [12]KernerBS.Criticismofgenerallyacceptedfundamentalsandmethodologiesoftrafficandtransportationtheory:Abriefreview[J].PhysicaA,2013,392(2):5261-5282. [13]MinOY,PanZZ,HongL,etal.Correlationanalysisofdifferentvulnerabilitymetricsonpowergrids[J].PhysicaA,2014,396(2):204-211. [14]HuP,FanWL,MeiSW.Identifyingnodeimportanceincomplexnetworks[J].PhysicaA,2015,429(3):169-176. [15]ZhangJH,XuXM,HongL,etal.Attackvulnerabilityofself-organizingnetworks[J].SafetyScience,2012,50(3):443-447.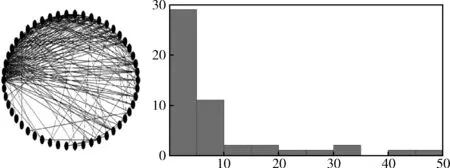

2 复杂网络可靠性函数
2.1 复杂网络可靠性函数的定义
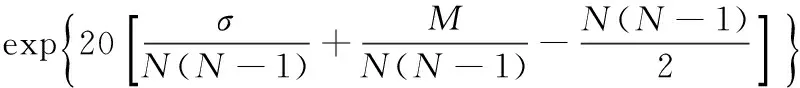
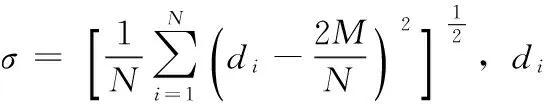
2.2 网络可靠性函数的性质
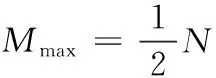

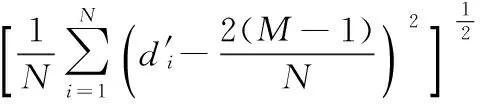
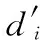
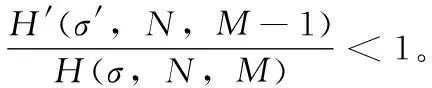
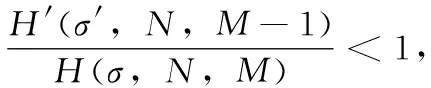
3 仿真分析
3.1 失效模式
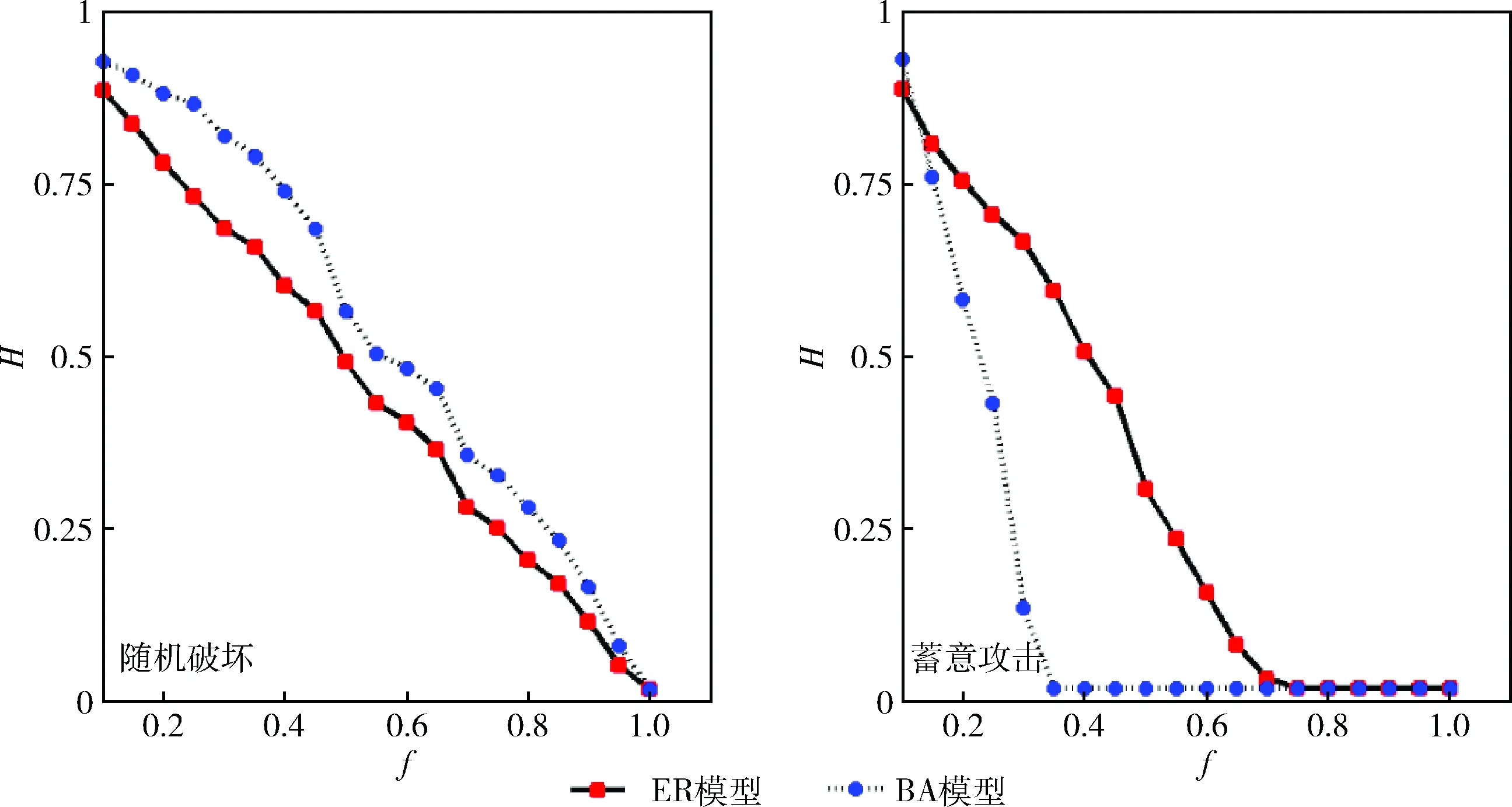
3.2 仿真结果及分析
4 结束语

