一种基于变结构控制的固体KKV快速开关伺服系统

文建刚，张竟飞，张 格，何 颐，周亚军

(中国航天科技集团公司四院四十一所，西安 710025)

0 引言

基于固体发动机的动能拦截器(固体KKV)采用直接力控制技术，利用姿、轨控发动机燃气流产生的推力来快速调整弹体姿态，具有更快的响应速度和更高的机动过载能力，有效提高了拦截器的机动性能和命中精度。这种主动姿态控制技术将得到越来越多的研究和应用。

由于姿轨控发动机及其燃气流控制特性差，是典型的非线性环节，难以产生大小连续可调的推力，无法实现有效的精度控制。因此，这类直接力伺服系统在实践中均采用开关控制来实现。对于非线性伺服元件，用开关控制能以较低的成本得到宏观上近似线性的控制效果。当前，成熟的开关控制有导弹的“bang-bang”舵控制、电机的PWM控制、开关电源(DC/DC)等。显然，开关控制的频率越高，控制精度越高，也越接近线性控制效果。因此，开关控制普遍有较高的响应快速性要求。

本文研究的快速开关伺服系统由电动伺服系统实现(传统上由电磁阀系统实现)。为提高响应快速性，通常采用高转速的伺服电机直接驱动负载，或仅采用减速比很小的减速器。由此带来的问题是相比带减速器的伺服系统，伺服电机的低速脉动现象“明显”，系统稳态精度差[1]；负载力矩与电机的输出力矩量级相当，且具有非线性、时变性特点，导致系统对负载扰动敏感，动态品质变差。

要解决上述问题，用线性的PID控制策略或简单的扰动补偿往往难以凑效。对于本文研究的系统，要使系统具有一定的自适应能力和较强的鲁棒性，变结构控制无疑是一种较理想的控制方案。

1 快速开关系统的变结构控制方案

变结构控制是一种非线性控制，不要求掌握受控对象的精确数学模型，其突出优点在于对参数摄动或变化以及外加扰动具有不变性，从而显示出很强的对不确定性因素的鲁棒性[2]。而变结构控制系统通常设计为高增益控制系统，动态响应快，带载能力强，尤其适用于快速开关控制系统。

本文设计的电动伺服系统为二阶系统。取偏差为X1，X2取为X1的微分。变结构控制系统需要设计一种反馈U(X1,X2)，并确定一条切换线S(X1,X2)。要求系统将状态变量X1和X2引导并限制在切换线S(X1,X2)上，使之沿着切换线向平衡点(原点)滑动收敛[3-4]。

变结构控制示意图如图1所示。

在滑动模态区有

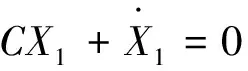
(1)

式(1)即为系统在滑动模态区的等价状态方程。在滑动模态区，系统表现为降阶(一阶)特性，它是一个完全独立于参数和扰动不确定性因素的自治系统。其时间常数为T=1/C。显然，系统在滑动模态区的动态性能只取决于设定的参数C。

2 变结构控制系统设计

2.1 直流伺服电机的模型

忽略电机的电气时间常数，并将负载视为扰动，可推导出电机的传递函数：

(2)

式中Ke为反电势系数；τm为机械时间常数。

在系统数字仿真与参数调试时，为了便于对系统施加负载扰动，通常采用如图2所示的模型[5]。

根据传递函数，可建立系统的状态方程。以位置指令Xi与反馈电位计输出电压X0之差(V)为变量X1，X2(V/s) 取为X1的微分，则有

X1=Xi-X0

在阶跃指令条件下:

故

(3)

因此，系统的状态方程可写为

(4)

2.2 变结构控制器设计

变结构控制是一种控制系统的综合方法，它的解不是唯一的，具有较大的灵活性。设计变结构控制器，主要有三种方法：根据能达条件设计、根据趋近律设计、利用相平面图设计[3]。

根据能达条件经过数学公式推导是一种普遍的设计方法，但这种方法不能完全确定控制参数，通常只能按某个充分条件进行设计，过于保守，极大限制了变结构控制系统的性能发挥。而趋近律的设计方法，虽然可控制趋近过程，提高正常运动阶段的品质。但根据趋近律设计的变结构系统极为复杂，不适合工程应用。因此，本文以相平面法进行控制器设计。

相平面法是分析一、二阶线性或非线性系统的图解方法，能较直观、准确、全面地表征系统的运动状态。用相平面图设计变结构系统，可更直观地看出系统的滑动模态能达条件。

设控制律为

代入式(4)，消去X2，当X1S>0时，可得

(5)

其特征根为

(6)

当X1S<0时，可得

(7)

此时，特征方程的根为

(8)

由此得到两种不同结构的控制系统。变结构控制系统中的所谓“变结构”，本质上是指系统内部的反馈控制器结构(包括反馈的极性和系数)所发生的不连续非线性切变。对于本文设计的变结构系统，就是要设计“变结构”的反馈控制器，使系统在上述两种不同结构的控制系统之间按由切换函数S决定的逻辑切换，形成一种具有滑动模态的新系统。

如果切换线的斜率C与图3(a)中收敛的那条渐进线的斜率λ2，满足：λ2

因此，滑动模态存在的条件为

(9)

为简便计，可设k>0，φ>0，令a1=-k，a2=k，b1=b2=φ，则控制律可简化为

(10)

滑动模态参数C的取值条件为

(11)

由此，设计的变结构系统如图5所示。

3 仿真与试验分析

3.1 空载条件仿真分析

本系统研究的开关伺服系统用于驱动燃气阀门，其开关行程为100°。因此，以100°阶跃指令进行仿真具有现实意义。

根据式(9)、式(10)，取k=10、φ=0.01、C=-4000，代入图5所示的系统。输入100°阶跃指令，在空载条件下得到图6所示的响应曲线和图7所示的系统相平面图。

从图6可知，系统在空载条件下约11 ms到达稳态值。从图7可看出，系统最大输出转速已达到电机的最大输出能力(15 000 (°)/s)。

3.2 加载条件下仿真分析

维持系统参数不变，向系统施加300 mN·m(实际系统负载扰动可能达到的最大极限值)阶跃负载，得到图8所示响应曲线和图9所示相平面图。从图8(a)、(b)可知，系统受扰后稳态值无明显变化。从图8(c)还可看出，同步施加与指令，响应时间从11 ms变为13 ms。可见，扰动对系统动态性能的影响也有限。

从图9可看出，加载条件下系统的最高输出转速有所下降(11 800 (°)/s)，这是电机的固有特性，但对位置环的影响较小。

为进一步验证变结构系统的抗扰能力，对系统施加750 mN·m负载，得到图10所示阶跃响应曲线。由图10可知，系统稳态误差有所增大(约1.2°)，响应时间由13 ms变为18 ms。可见，系统在非常大的负载扰动下仍表现出优良的性能，表明设计的变结构系统具有较强的鲁棒性。

3.3 高频响应特性分析

图11是系统的实际高频工作试验曲线。由于本系统实际用于开关控制，因此用高频大角度方波输入(30 Hz，95°)取代正弦输入对系统的快速性(频响)进行考核更具有现实意义。

从试验曲线可看出，系统在高频大角度方波输入条件下，其快速性远大高于一般的伺服系统。按照幅频带宽的定义，系统在大角度条件下的带宽远高于30 Hz。

3.4 各参数对系统性能的影响

变结构系统的性能取决于两方面因素，即滑动模态本身的参数，以及控制增益。如前所述滑动模态表现为降阶特性，系统在滑动模态区的动态性能只取决于设定的参数C，C越大，时间常数T=1/C越小，响应越快。而在非滑动模态区，系统仍为二阶特性，其动态性能决定于控制增益k和φ的大小，k和φ的值越大，系统的动态响应就越快，系统鲁棒性越强[6-8]。

当然，C、k和φ的值太大也会增大系统的超调或加剧震荡，影响稳态性能。本系统用于阀门的快速开关控制，追求快速性是主要目标。而在保证阀门有效开闭的前提下，超调及稳态性能可以适当放宽。

因此，在满足式(10)、式(11)的前提下，可适当增大C、k和φ的值，有助于提高系统响应快速性，增大系统带宽，提高系统带负载能力和鲁棒性。

3.5 颤振问题

颤振是变结构系统不可避免的问题。在本系统中，由于参数C取值很大，切换线非常靠近Y轴，而控制律又设计为X1的线性函数，因此在Y轴附近的控制量非常小，从而在靠近Y轴的切换线上产生的颤振量级也非常小。此外，系统较大的负载力矩也有助于减小颤振。

对于本系统，以实现快速开关为主要目的，而颤振的量级小、危害小。因此，颤振问题可不作为关注重点。

4 结论

(1)本文设计的变结构开关伺服系统，对“强负载扰动”表现出了较强的自适应能力，系统具有较强的鲁棒性；

(2)变结构系统是一种高增益控制系统，能大大提高系统的动态性能，尤其适用于快速开关系统；

(3)用相平面法进行变结构控制系统的设计和参数调试简单、直观，是一种较为实用的设计方法。

[1] 裴涛，冉树成.位置伺服系统低速运动特性的研究[J].水运科学研究所学报,1997(3,4):17-24.

PEI Tao,RAN Shucheng.Research of slow-speed motion in positioning servo system[J].Journal of Waterborne Transportation Institute,1997(3,4):17-24.

[2] 陈新海,李言俊,周军.自适应控制及应用[M].西安：西北工业大学出版社,1998.

CHEN Xinhai,LI Yanjun,ZHOU Jun.Adaptive control and its application[M].Northwestern Polytechnical University Press,1998.

[3] 高为炳.变结构控制理论基础[M].北京：中国科学技术出版社,1990.

GAO Weibin. Foundation of variable structure control theory[M].Chinese Science and Technology Press,1998.

[4] 胡祐德，马东升，张莉松.伺服系统原理与设计[M].北京理工大学出版社,1999.

HU Youde,MA Dongsheng,ZHANG Lisong. The principle and design of servo system[M].Beijing Institute of Technology Press,1999.

[5] 梅晓榕，柏桂珍，张卯瑞.自动控制元件及线路[M].北京：科学出版社,2005.

MEI Xiaorong,BAI Guizhen,ZHANG Maorui.Automatic control components and circuit[M].Science Press,2005.

[6] 周军.变结构控制理论在导弹电动舵机系统设计中的应用[J].西北工业大学学报,1990,8(3):273-280.

ZHOU Jun.Application of variable structure control theory in electric servo system design[J].Journal of Northwestern Polytechnical University,1990,8(3):273-280.

[7] 王江,王家军.电力电子开关变换器的滑模控制[J].电机与控制学报,2000,4(3):188-192.

WANG Jiang,WANG Jiajun.Sliding mode control of power electronic switching converters[J].Electric Machines and Control,2000,4(3):188-192.

[8] 绛海萍，郑载满.基于切换函数超前补偿的滑模变结构控制[J].电气传动自动化,1997,19(12):32-35.

JIANG Haipin,ZHENG Zaiman.Sliding mode variable structure control based on forward compensation for switching function[J].Electric Drive Automation,1997,19(12):32-35.