固体火箭发动机径向加质圆管模型流动稳定性的参数分析

李 阳，刘佩进，金秉宁

(西北工业大学 燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

国内外大型分段固体火箭发动机经常出现低频率的压强振荡现象[1-4]。研究发现，大部分的压强振荡都是由于周期性涡脱落所引起的[5]。由于对涡脱落自身形成和发展规律的认识不足，且对涡脱落与发动机声场之间相互作用的研究不足，目前工程上还没有实用方法预示涡脱落和压强振荡。涡脱落与声场的耦合可利用高精度CFD模拟[6]，但由于发动机几何尺寸大，工作时间长，对每一时刻的工作状态进行CFD计算并不现实。从流动稳定性理论出发，对涡脱落与声场耦合的机理进行研究，获得流动稳定特征以及演化规律，是当前学术界的研究热点[7]。

Flandro利用流动稳定性理论和能量平衡方法，建立了固体火箭发动机内的涡声耦合模型，在动量方程中引入局部体积力来描述涡的反馈效果，计算了由涡脱落产生的能量增长指数[8]。而Vuillot将Flandro的方法用到实验发动机C1x的设计过程中时，发现局部体积力的引入具有较大的任意性，计算结果敏感地依赖涡从下游撞击点到剪切层原点的距离(此距离并非确定值，且有一定估计偏差)。因此，结果的可靠性不足[9]。Griffond采用局部非平行方法，计算了特定工况下Taylor-Culick流的稳定性，并与Dunlap[10]的冷流实验做了比较，得到了两个特定工况下的不稳定模态。但中性曲线的分析仅描述了特定工况下方程解的分布，并不适合描述物理过程[11]。Akiki研究可压缩Taylor平面流的稳定性时，数值方法与解析方法分别计算得到的幅值出现偏差，他认为是解析方法把有旋量和无旋量分开的求解过程造成的[12]。但Chedevergne发现解析方法得到的流动稳定性模态可叠加，并能准确地重现DNS结果。因此，Akiki的解释并不令人信服[13]。杨尚荣[6]应用局部非平行理论，分析了由主变量公式和流函数公式导出的扰动方程的差异，发现在不发生共振的情况下，理论方法可预估发动机内的流动不稳定频率，但并未讨论理论方法在火箭发动机流动稳定性预估计算中的实际应用。

本文利用谱配置方法，对不同结构及工况下的Taylor-Culick流进行分析，研究结构参数、流动扰动参数变化对稳定性的影响。本文讨论了对固体火箭发动机进行稳定性预估时，侧向注入雷诺数、长径比、频率、环向波数与空间稳定性的相互关系，得到了不稳定模态的变化规律。

1 控制方程与求解方法

本文研究的径向加质Taylor-Culick流模型，是固体火箭发动机燃烧室前部内流场的一种简化模型，模型中不包含喷管附近的高马赫数流动部分，几何构型与坐标如图1所示。固体火箭发动机前部的燃烧室，流动马赫数小于0.3，适合采用不可压流体控制方程。

利用归一化参考量(半径R、径向加质速度Vinj、密度ρ*、运动粘性系数υ)对不可压粘性流体N-S方程进行无量纲化。将归一化N-S方程中的瞬时变量分解为平均量和扰动量之和，得到关于扰动量的方程：

▽·u′=0

(1)

平均量作为基本流可以求出解析解：

(2)

利用分离变量法，假设扰动量为简正模态形式：

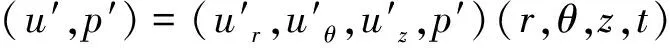
=(ur,uθ,uz,p)(r)ei(mθ+αz-ωt)

(3)

其中，ω为实数，代表无量纲扰动频率；α=αr-iαi为复数，实部αr为轴向扰动波数，负虚部-αi为轴向扰动增长率。m为正整数，代表环向波数。进行空间稳定性分析时，给定频率ω和环向波数m，利用谱配置方法可求得任意轴向位置z处的增长率-αi和波数αr。

将简正形式的扰动量代入扰动方程，可化为如下关于α的多项式的特征值问题：

(4)

Taylor-Culick流的边界条件为壁面上和对称轴上的速度边界条件：头部壁面速度为零、侧壁上注入速度为常数、侧壁上轴向速度无滑移以及对称轴上的径向速度对称条件。利用扰动量表示物理边界条件，得到扰动方程的齐次边界条件。利用扰动方程，还可得到压力边界条件。

(ur，uθ，uz)(±1)=0,Dp(±1)=0

(5)

利用谱配置方法，选择切比雪夫多项式Tk(x)=cos(karccos(x))进行空间离散；配置点选择Gauss-Lobatto积分点：

(6)

权函数α(x)=1。通过MatLab编程计算得到相应结果[14-15]。

2 计算结果与讨论

2.1 计算结果验证

作为验证，计算了长径比z=10，侧向注入雷诺数Re=4500，频率ω=80，环向波数m=0下的轴向波数、轴向增长率与不稳定模态，得到的特征谱如图2所示。图2中，两个不稳定点即为两个不稳定模态，对应的横坐标为轴向波数、纵坐标为轴向增长率。Griffond通过设定初值，并利用泰勒展开的牛顿-拉夫森迭代法计算了相应结果，其定性分析与dunlop实验结果[10]没有矛盾。本文结果与Griffond的结果[11]比较，如表1所示。

本文所得结果与文献结果基本吻合，可验证本文所用方法可行。

利用谱方法计算的结果，通过侧向注入雷诺数Re、长径比z、频率ω及环向波数m的变化与轴向波数的关系，来讨论流动不稳定现象。计算结果基于归一化扰动方程，量纲为1，对于不同的物理构型及物理量，可换算成真实数值。定性分析利用无量纲参变量代替物理数值。

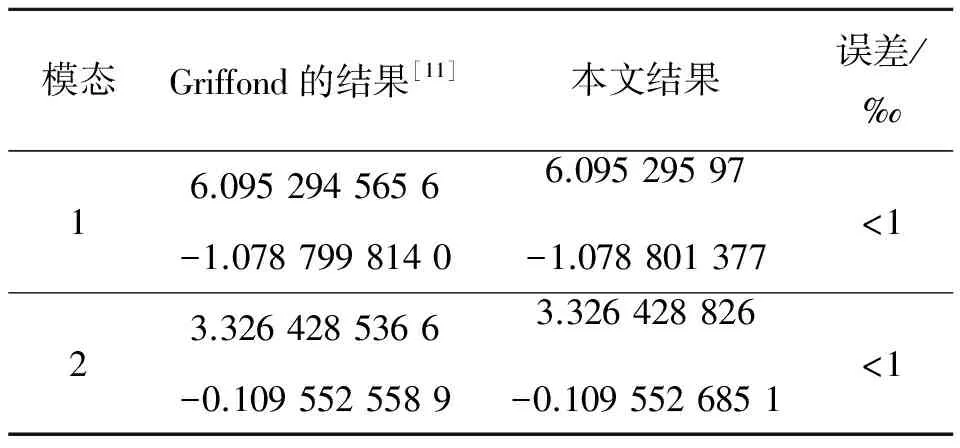
模态Griffond的结果[11]本文结果误差/‰16．09529456566．09529597-1．0787998140-1．078801377<123．32642853663．326428826-0．1095525589-0．1095526851<1

2.2 侧向注入雷诺数的影响

侧向注入雷诺数定义为Re=RVinj/υ，其中R为圆管半径，不可压缩流体运动粘度系数为常数。不可压缩流体的密度为常数，动力粘度确定后，运动粘度系数也随之确定。由定义可知，当圆管半径一定时，加质速度越大，侧向注入雷诺数越大。因此，侧向注入雷诺数的变化反映了径向加质速度变化对流动不稳定的影响。

在不同侧向注入雷诺数下，流动会产生不同的状态。低侧向注入雷诺数不易出现不稳定情况，随着侧向注入雷诺数增大产生的不稳定模态增多(对于图3中情况，对应不稳定模态增加的侧向注入雷诺数临界值约为100、750)。不同的不稳定点随侧向注入雷诺数变化的趋势并不相同。不稳定点1是最早出现的对应于小侧向注入雷诺数的波动，随着侧向注入雷诺数增大，其轴向波数及波动增长率都是不断增大的，侧向注入雷诺数在1500以内时，频率和增长率增幅较大，而随后增幅趋缓，并逐渐趋近于有限值。这种现象符合物理规律，不稳定波动并不是无限增大的。不稳定点2点对应于中侧向注入雷诺数波动，此点在侧向注入雷诺数达到一定程度时才会出现，轴向增长率逐渐增大，并趋近于有限值，而轴向波数逐渐减小逐渐由高频变为低频。所以，随着侧向注入雷诺数的增加，高低频不稳定模态会发生转换。这意味着某些工作状态下(如侧向加质雷诺数的变化过程中对应的波动频率正好跨过某一阶声腔频率)，更易引发流动不稳定。

固体火箭发动机内是大雷诺数流动，一般在103量级，上文讨论范围选取0～7000，仅为全面反映TC流模型侧向加质雷诺数的影响，固体火箭发动机的讨论限定在图3中大侧向加质雷诺数的部分。

2.3 长径比的影响

对于本文所述模型，长径比是固体火箭发动机内燃气流动空腔的物理表征。固体火箭发动机长径比超过10称为大长径比发动机，但一般不会超过15。为直观地反映长径比变化引起不稳定性变化的趋势、描述流动不稳定的物理现象，本文选取长径比范围0～15。图4为长径比的变化对特征值的影响，反映了物理构型与流动稳定性的关系。

由图4可看出，当长径比增加，特征值有两段变化趋势。当长径比小于3.5时，随着长径比的增加，轴向波数急剧下降，而轴向增长率急剧增长；当长径比大于3.5时，轴向波数及增长率都随着长径比的增加而缓慢降低。这与物理现象是内在一致的，当长径比小于3.5时，均匀流场流线曲率大，加质注入的速度激励及速度方向的改变对不稳定的增长作用很大；当长径比大于3.5时，均匀流场流线近似平行于轴向，表现为均匀流场对轴向不稳定的阻尼增强，轴向增长率以指数形式变化，并趋于稳定值。

在发动机设计中，除了要避开声共振的固有频率外，还要注意构型对流动不稳定的影响，特别要注意长径比为3.5的构型。此时，扰动的放大效果最强，较小的扰动便可产生较大幅度的振动，不利于发动机正常工作。长径比对不稳定性的影响体现在对扰动的放大效果上，并不意味着长径比为3.5时，流动不稳定性最易发生。

2.4 频率的影响

ω表示时间方向上的波动频率，其量纲化公式为

频率在一定范围内对于空间稳定性产生影响，计算得到频率ω影响范围为无量纲区间[50, 190]，见图5。

不稳定模态数量(即不稳定点数)会随着频率的增长而变化，见图5。频率达到66～67时，不稳定点由出现一个变为两个(1→2)；频率在之后达到116～117、156～157、182～183以及188～189时，不稳定点数分别出现由(2→3)、(3→2)、(2→1)以及(1→0)的变化。但不管出现多少不稳定点，其变化规律是相同的，轴向不稳定波数不断增长，新的低频轴向不稳定模态不断出现；而当频率达到一定的值后，流动不稳定模态消失，流动变为空间稳定；不稳定的轴向增长率都是先增加后达到极值，然后快速减小。可见，时间波动与空间波动并不是同步的，随着频率的增强，空间波动先增强、再减小，然后变为稳定流动。在工程中发展对流动不稳定的抑制方法时，可利用此特性。

2.5 环向波数的影响

环向波数m在扰动方程的参量中表现为eimθ，环向波数增大，则环向波动频率增大。对于小扰动，理论上环向与轴向波数应在同一量级，数值计算得到同样的结果。

图6为环向波数变化对轴向波数与轴向增长率的影响。随着环向波数的变化，不稳定模态的个数也发生变化。从特征谱(图7)中可了解到，随着环向波数的增加，不稳定点(图中右下角三点沿轴向依次为Ⅰ、Ⅱ、Ⅲ点)逐渐由不稳定模态变为稳定模态，不同的不稳定点其变化规律是相同的，其中不稳定点Ⅱ、Ⅲ最具有代表性。随着环向波数的增加，轴向波数在一定范围内增加(见图6(a))，这说明各坐标上的空间不稳定是协同的，表现为频率的共同增长；但随着环向波数继续增大，轴向波数却随之迅速减小(见图6(b))，表现为频率的迁移。轴向增长率却是逐渐减小，最后变为稳定点。综合来看，流动不稳定效果在轴向、径向以及切向上表现为频率共同增长，波数此消彼长。

3 结论

(1)侧向注入雷诺数决定基频不稳定模态，随着侧向注入雷诺数增大，振荡模态可能增加，振荡频率可能发生由高频变为低频的转换；侧向注入雷诺数影响振荡幅值的放大比率，侧向注入雷诺数越大，轴向不稳定振幅放大率越大。

(2)构型长径比为3.5的固体火箭发动机在发生压强不稳定振荡时的轴向增长率最大，较小的扰动便有可能产生较大振动。

(3)频率范围影响空间不稳定出现的可能性，可利用此特性发展对固体火箭发动机发生流动不稳定主动抑制的方法；环向波数影响不稳定模态数目，环向波数与轴向波数具有相关性，幅度总和趋于有限值。

[1] 刘佩进,魏少娟,杨尚荣.固体火箭发动机非线性燃烧稳定分析方法[J].固体火箭技术,2013,36(3):302-309.

LIU Peijin,WEI Shaojuan,YANG Shangrong.Nonlinear combustion instability analysis method of solid rocket motor[J].Journal of Solid Rocket Technology,2013,36(3):302-309.

[2] 吴亚可,何国强,刘佩进,等．潜入式喷管背区空腔对压强振荡及旋涡运动影响的实验研究[J].固体火箭技术,2010,33(6):621-625.

WU Yake,HE Guoqiang,LIU Peijin,et al.Experimental study of influence of cavity formed by submerged nozzle on pressure oscillation and vortices motion[J].Journal of Solid Rocket Technology,2010,33(6):621-625.

[3] 王建儒,何国强,许团委,等.燃烧室对接狭缝设计参数对压强振荡的影响研究[J].固体火箭技术,2012,35(4):474-478+484.

WANG Jianru,HE Guoqiang,XU Tuanwei,et al.Effect of internal joint design parameters on pressure oscillation in combustion chamber[J].Journal of Solid Rocket Technology,2012,35(4):474-478+484.

[4] 张翔宇,何国强,刘佩进.轴对称后向台阶不稳定流动及压强振荡数值研究[J].固体火箭技术,2012,35(2):171-176+182.

ZhANG Xiangyu,HE Guoqiang,LIU Peijin.Numerical study on unsteady backward-facing step flow and pressure oscillations[J].Journal of Solid Rocket Technology,2012,35(2):171-176+182.

[5] 刘佩进,杨尚荣.分段固体火箭发动机中声涡耦合现象的实验研究现状[J].固体火箭技术,2012,35(6):726-731.

LIU Peijin,YANG Shangrong.An overview on experimental study of vortex-acoustic coupling in segmented solid rocket motors[J].Journal of Solid Rocket Technology,2012,35(6):726-731.

[6] 李强,何国强,刘佩进,等.模型固体火箭发动机内涡脱落过程的大涡模拟[J].推进技术,2005,26(6):481-484.

LI Qiang,HE Guoqiang,LIU Peijin,et al.Large eddy simulation of vortex shedding for model SRM[J].Journal of Propulsion Technology,2005,26(6):481-484.

[7] 杨尚荣,刘佩进,魏祥庚,等.固体火箭发动机径向加质流局部稳定性分析方法研究[J].推进技术,2013,34(7):925-931.

YANG Shangrong,LIU Peijin,WEI Xianggeng,et al.A study of analysis method for hydrodynamic stabilities of solid rocket motors with side-induced flow[J].Journal of Propulsion Technology,2013,34(7):925-931.

[8] Flandro G A.Vortex driving mechanisms in oscillatory rocket flows[J].AIAA Journal,1986,2(3):206-214.

[9] Vuillot F.Vortex-shedding phenomena in solid rocket motors[J].Journal of Propulsion and Power,1995,11(4):626-639.

[10] Dunlap R,Blackner A M,Waugh R C,et al.Internal flow field studies in a simulated cylindrical port rocket chamber[J].Journal of Propulsion and Power,1990,6(6):690-704.

[11] Griffond J,Casalis G and Pineau J P.Spatial instability of flow in a semi infinite cylinder with fluid injection through its porous walls[J].European Journal of Mechanics.B/Fluids,2000,19(1):69-87.

[12] Akiki M,Batterson J W and Majdalani J.Biglobal stability of compressible flow fields.part 2:application to solid rocket motors[R].AIAA 2013-3866.

[13] Chedevergne F,Casalis G and Majdalani J.Direct numerical simulation and biglobal stability investigations of the gaseous motion in solid rocket motors[J].Journal of Fluid Mechanics,2012,706(3):190-218.

[14] 何松年.谱方法及其应用[J].中国民航学院学报(综合版),2000,18(6):30-33.

HE Songnian.Spectral method and its application[J].Journal of Civil Aviation University of China,2000,18(6):30-33.

[15] 孙德军,尹协远,童秉纲.关于Orr-Sommerfeld方程的Chebyshev谱方法的讨论[J].上海力学,1998(1):1-8.SUN Dejun,YIN Xieyuan,TONG Binggang.On Chebyshev spectral methods for the Orr-Sommerfeld equation[J].Chinese Quarterly of Mechanics,1998(1):1-8.