多臂空间机器人的视觉伺服与协调控制

冯 骁，卢 山，侯月阳，王奉文，贾英宏

(1. 北京航空航天大学宇航学院，北京 100083；2. 上海航天控制技术研究所，上海 201109；3. 上海市空间智能控制技术重点实验室，上海 201109)

0 引 言

由于太空环境的危险性，使用空间机器人代替航天员进行在轨操作已成为一个重要的研究课题[1]。具有多部机械臂的空间机器人能够完成复杂的操作，已成为空间机器人设计的重要发展方向。通常，航天器与地面间存在通信延迟，增强空间机器人执行任务的自动化程度将有助于提高其执行任务的效率。因此，多臂空间机器人自主在轨操作的相关技术具有研究和应用价值。关于空间机器人技术的详细综述可以参考文献[1]和文献[2]，下面仅介绍本文内容相关的现有成果。

对多臂空间机器人本身及其与目标间相对运动的建模是实现自主在轨抓捕的基础。利用Kane方法导出多体系统动力学的过程简单而有序，因此受到许多研究者的注意。文献[3]利用Kane方程导出了任意树形拓扑构型柔性多体系统的动力学方程，其形式适合计算机编程实现。文献[4]建立递推运动学关系，文献[5]引入偏速度、偏角速度矩阵，简化了运动学变量求解公式的形式。以这些动力学模型为基础编写的软件已在实践中应用。

融入视觉信息的轨迹规划是实现自主在轨抓捕的关键。由于目标相对航天器平台的运动存在不确定性，需要对运动的状态进行测量，并将测量信息引入机械臂的轨迹规划中，使机械臂能根据目标运动的情况调整自身运动。使用手眼相机拍摄目标[6]并采用视觉伺服算法[7]是实现上述功能的一种较为成熟的方案。文献[6]将基于位置的视觉伺服用于双臂空间机器人的在线轨迹规划，文献[8]则在工程项目中验证了类似方法在单臂空间机器人系统中的适用性。仅使用视觉伺服进行规划得到的机械臂运动会对航天器平台造成较大的姿态扰动。文献[9]提出冗余机械臂在反作用零空间中运动时不会造成平台姿态扰动，这样的运动称为零反作用机动。但对单臂空间机器人而言，进行零反作用机动时末端作用器的运动范围十分有限。文献[10]利用受限最小干扰图对双臂空间机器人进行轨迹规划，使平台姿态在机械臂运动过程中基本保持不变。空间多臂机器人在线轨迹规划的一个新进展是将视觉伺服与零反作用机动相结合，使机械臂在对平台无扰动的约束下抓捕目标，这一方法使用基于图像的视觉伺服，直接使用图片特征作为测量量[11]。将视觉伺服的另一类方法(基于位置的视觉伺服)与零反作用机动结合的研究则比较少见。

由于零反作用机动的运动范围有限，当不能在轨迹规划中消除机械臂对平台的扰动时，需要协调地控制机械臂与平台。文献[12]从角动量层面推导协调关系，在平台和机械臂各自独立控制系统的基础上建立协调控制器，通过前馈补偿机械臂对平台的扰动。这一方法的工程实现可参见文献[13]，文献[14]也采用了类似的方法。这种协调控制方法一方面可以保留平台和机械臂已有的(经过实践检验的)控制器设计，另一方面又在控制器中引入了平台与机械臂的相互作用，十分适合工程应用。除了从角动量层面建立协调控制器，还可以基于系统整体动力学模型导出协调控制机械臂与平台的逆动力学控制器，其思路更简明，控制性能更容易预测。另外，对于空间机器人插拔模块的过程，文献[15]研究了其力/位置混合控制方法。对于多臂空间机器人协调操作载荷的任务，文献[16]则提出了位置/内力的混合控制策略。

虽然空间机器人的建模、视觉伺服轨迹规划和协调控制都有较为成熟的方法，但适用于多臂空间机器人系统工程应用的综合方案尚不多见。如何将这些方法结合在一起解决多臂航天器的自主在轨操作问题并不十分清晰。另一方面，有必要建立结合基于位置的视觉伺服和零反作用机动的方法。本文提出一种适用于多臂空间机器人的建模、视觉伺服与协调控制的方案，并结合基于位置的视觉伺服与零反作用机动建立一种在线轨迹规划方法。为了验证算法和进行仿真分析，基于Matlab编写了多臂空间机器人仿真(Multi-arm space-robot simulation,MASS)软件。

1 系统描述与运动学、动力学建模

1.1 系统描述

多臂空间机器人自主抓捕的示意图如图 1所示。其中多臂空间机器人由一个航天器平台和L部安装在其上的机械臂构成，平台具有力、力矩执行机构和一部测量目标位置的相机，第i部机械臂有Ni个电机驱动的旋转关节，每部机械臂的末端安装有一部用于视觉测量的手眼相机。

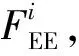
1.2 运动学建模

航天器平台的运动学为

(1)

式中：rb为Fb原点在FI中的位置；Rb为Fb到FI的坐标转换阵；vb为Fb原点相对FI的速度在Fb中的投影；Θb为Fb相对FI的姿态角，本文使用3-1-2姿态角(ψ,φ,θ)；G(Θb)由姿态角的转轴列阵排列而成，表示姿态角变化率与角速度间的线性关系；ωb为Fb相对FI的角速度在Fb中的投影；变量上的点表示时间导数。

Ft原点相对Fb运动的关系为

(2)

(3)

(4)

(5)

(6)

对第i部机械臂引入其关节角列阵qi。rb,Θb和qi(i=1,2,…,L)组成了多臂空间机器人的广义坐标y,

(7)

(8)

1.3 动力学建模

Kane方法通过将力矢量向偏速度方向投影而消去多体系统中的约束力，导出多体的动力学方程，适合用于多臂空间机器人的动力学建模。

使用文献[5]中矩阵形式的Kane方法，可将系统的动力学方程写为

(9)

式中：FA为作用于系统上的广义主动力,M为广义质量矩阵,FIt为非线性广义惯性力。不考虑环境对空间机器人的作用时，有

(10)

式中：Fb为作用于平台的主动力系的主矢在Fb中的投影,Tb为作用于平台的主动力系对Fb原点的主矩在Fb中的投影,τi为第i部机械臂的关节力矩组成的列阵。M,FIt可由系统中各体的贡献求和得到：

(11)

(12)

各体对质量阵和非线性广义惯性力贡献的求解方法可参考文献[5]。

2 视觉伺服

2.1 基于位置的视觉伺服

机械臂对平台的扰动及目标本身的运动会导致目标相对Fb运动，因此需在机械臂的轨迹规划中引入对目标的测量，并进行在线的轨迹规划，视觉伺服是一种比较成熟的实现方法。本文参照文献[7]，使用基于位置的视觉伺服方法。

(13)

(14)

(15)

结合机械臂的几何雅克比矩阵，有

(16)

式中：

(17)

(18)

式中:iJ(qi)为第i部机械臂的几何雅克比矩阵。

对于无冗余的机械臂(6自由度)，可以使用速率分解规划公式

(19)

式中：Ki为对称正定矩阵。在关节角控制较好，即qi≈qr(i)时，有

(20)

抓捕误差将收敛到零。

2.2 零反作用轨迹规划

对于具有冗余的机械臂，轨迹规划可使用伪逆解

(21)

对于无外力作用的多臂空间机器人系统，在初始静止的条件下，其对平台质心的角动量L0有表达式[12]

(22)

式中：Is为与平台运动相关的惯量，Im(i)为与机械臂相关的惯量。由于Is始终可逆，机械臂不对平台产生扰动的条件是

(23)

观察式(23)可知其并不要求各项单独为零，这一数学表述的物理意义是，多臂航天器的零反作用机动是协调进行的，其中存在各臂间扰动抵消的情况。

由于系统冗余自由度数目及机械臂几何、质量参数和构型的限制，一般很难使用零反作用运动实现对目标的精确抓捕。因此，在每一时刻构造、求解约束最小二乘问题：

(24)

可见，约束要求多臂航天器的机械臂严格在零反作用空间中运动；指标函数则是对精确抓捕的放松，其物理意义是尽量使机械臂末端与目标间的误差减小。

(25)

3 协调控制器设计

零反作用机动能够使平台姿态不受机械臂运动的扰动，但利用这一机动可达到的空间一般是有限的。为了精确地抓捕目标，需在抓捕的最后阶段关闭零反作用机动功能，使用式(19)或(21)而不是式(25)的结果进行轨迹规划。这时，机械臂运动将对平台产生不可忽视的扰动，需要协调地控制机械臂和平台的运动。在工程应用中，平台的控制系统和机械臂的控制系统往往是相互独立设计的，由于机械臂运动对平台的扰动难以被常规的平台控制系统补偿，需要建立在独立控制系统之上的协调控制器，使平台控制力矩及时补偿扰动。若希望建立平台、机械臂的一体化控制器，基于多臂航天器系统的动力学模型设计逆动力学控制器则是一种常用的方法，可以充分考虑机械臂与平台间的运动耦合关系。本文采用以上两种方法构建多臂空间机器人的协调控制器。

3.1 基于角动量前馈补偿的协调控制算法

假设平台与机械臂的独立控制系统已经设计完成(平台控制系统包括姿态控制与目标相对位置控制，基于平台动力学模型和式(1)～(4)的运动学关系设计)。但基于反馈的姿态控制系统往往不能及时补偿机械臂运动对姿态造成的扰动，需要在考虑机械臂与平台运动耦合的基础上进行补偿。与建立零反作用机动的方法类似，为了导出协调控制算法，仍由角动量表达式出发，并假设系统初始时静止，但此时平台上有主动控制力矩的作用，即

(26)

(27)

式中：T0为作用于平台的主动力系对平台质心的主矩在Fb中的投影。为了保持平台姿态不受扰动，应使外力矩的积分与机械臂运动的角动量完全相同，即

(28)

在实际中，为了防止前馈导致的不稳定，可以通过前馈系数Kff对前馈角动量进行调节，最终取前馈补偿规律为

(29)

对于可以接受角动量指令的执行机构，可以将前馈角动量直接加入指令中

hd=hff+hf b

(30)

式中：hd为包含平台反馈控制与前馈补偿作用的总角动量指令，hf b为平台姿态控制系统(反馈控制)产生的角动量指令。对于接受力矩指令的执行机构,则可以再设置一个角动量控制回路，使执行机构提供的角动量跟踪期望值。

(31)

式中：Km为对称正定的控制增益矩阵，h为T0作用积累的角动量。

3.2 逆动力学控制算法

基于角动量前馈补偿的协调控制在平台和机械臂相互独立的控制系统上构建了基于角动量关系的前馈补偿机制，使得平台的姿态控制系统能够获取机械臂运动产生的扰动量并进行补偿。更进一步，可以在多臂空间机器人系统动力学模型的基础上设计同时控制平台和机械臂运动的逆动力学控制器。

由系统的动力学方程出发

(32)

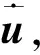
(33)

4 仿真校验

为了校验上述视觉伺服与协调控制算法，对双臂空间机器人自主抓捕目标航天器上两个对称目标点的任务进行仿真。图2为系统的示意图。航天器平台质量接近2 t。两机械臂的构型相同，对称安装在平台z轴的正、负方向，其中+z方向的称为机械臂1，-z方向的称为机械臂2。每部机械臂重约70 kg，长约4 m，有7个关节。Ft的原点不运动，姿态相对FI作姿态角3°,角速度0.3°/s的晃动(Ft，FI的定义参见图 1)。

首先考虑不对平台施加主动控制，而使机械臂在视觉伺服下进行自主抓捕的情况(称为算例1)，图3为其系统框图。这一情况将被作为对比的基线。在轨迹规划中，对每个关节施加2°/s的关节转速限制。仿真结果如图4～图11所示。由图4～图7可知，机械臂1和机械臂2均能准确完成抓捕目标的任务。但是，目标航天器在Fb内的位置距期望值(Fb中的一个固定位置)有较大的偏移，且Fb的姿态也有比较大的摆动。从这一结果可以看出使用零反作用轨迹规划对平台进行控制的必要性。

其次，考虑将零反作用机动引入在线轨迹规划的情况(称为算例2)，图12为其系统框图。在机械臂初始构型、目标均对称的情况下，机械臂1与机械臂2对平台产生的扰动会比较精确地相互抵消，这使得精确抓捕任务在零反作用机动下就可以完成。但这种情况在机械臂任务中是比较特殊和少见的。因此，为了使结果更具有一般化的意义，在仿真中将机械臂1与机械臂2的初始构型作不同的设置。仿真结果如图13～图18所示。因为零反作用轨迹规划优先保证对平台的无扰动，而将机械臂对目标的抓捕作为优化目标，所以引入零反作用轨迹规划后，机械臂对目标的抓捕出现了一定的偏差，而平台的姿态则不受扰动(注意到姿态角误差数量均在10-5(°)级别)。在实际中，可以先使机械臂沿零反作用轨迹运动，靠近目标后再切换成常规的视觉伺服，完成精确抓捕。

最后，考虑不使用零反作用轨迹规划时对平台进行控制。控制目标为机械臂精确抓捕目标，同时平台保持其相对目标航天器系原点的位置并镇定自身的姿态。

一方面，使用基于角动量前馈补偿的协调控制方法(称为算例3)，图19为系统框图，角动量前馈系数取为0.8。机械臂抓捕的结果与基线情况类似，但不包含平台随机械臂运动时机械臂进行的附加运动。平台的控制结果如图20～图25所示。目标航天器相对平台的位置误差和平台的姿态误差相比基线仿真明显降低，说明了这一协调控制方法的有效性。从机械臂对平台的扰动力矩和平台控制力矩的对比可以看出，大部分扰动力矩及时地被平台控制力矩补偿，其对平台姿态造成的影响被有效降低。

另一方面，在逆动力学控制下(见图26)，机械臂的控制效果与基于角动量前馈补偿的协调控制基本一致，而由于控制器是在整个系统的动力学模型上设计的全状态反馈控制器，其可以完全消除机械臂运动带来的平台扰动，平台控制力、力矩完全补偿机械臂对平台的扰动力、力矩。

5 MASS软件设计

在上述理论的基础上，使用Matlab编写了仿真软件MASS。其具有多臂空间机器人动力学、运动学仿真能力，并可由用户自定义控制作用和输出(第2、第3节的轨迹规划与控制算法已通过这一接口实现)。

MASS的核心是多臂空间机器人的系统常微分方程求解器，求解动力学、运动学方程

(34)

(35)

和用户自定义控制器

FA=fc(t,y,u,z)

(36)

(37)

组成的一阶常微分方程系统。另外，用户可自定义输出变量，对仿真结果作详细的分析。

6 结 论

本文研究多臂空间机器人自主抓捕技术中的视觉伺服与协调控制问题。研究结果表明：多臂空间机器人可实现各臂对各自目标的抓捕，利用视觉伺服进行在线轨迹规划、进而实现自主抓捕具有可行性；零反作用机动可以有效消除机械臂对平台姿态的扰动，对提高平台姿态控制精度具有显著作用；基于角动量前馈补偿的协调控制器和逆动力学控制器均可实现对系统的协调控制，前者相对简单且更接近工程应用，后者更易理解但计算相对复杂。

[1] Flores-Abad A, Ma O, Pham K, et al. A review of space robotics technologies for on-orbit servicing [J]. Progress in Aerospace Sciences, 2014, 68: 1-26.

[2] Xu W, Liang B, Xu Y. Survey of modeling, planning, and ground verification of space robotic systems [J]. Acta Astronautica, 2011, 68(11): 1629-1649.

[3] Singh R P, VanderVoort R J, Likins P W. Dynamics of flexible bodies in tree topology-a computer-oriented approach [J]. Journal of Guidance, Control, and Dynamics, 1985, 8(5): 584-590.

[4] Banerjee A K, Lemak M E. Multi-flexible body dynamics capturing motion-induced stiffness [J]. ASME, Transactions, Journal of Applied Mechanics, 1991, 58: 766-775.

[5] 胡权, 贾英宏, 徐世杰. 多体系统动力学 Kane 方法的改进 [J]. 力学学报, 2011, 43(5): 968-972. [Hu Quan, Jia Ying-hong, Xu Shi-jie. An improved Kane’s method for multibody dynamics [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 968-972.]

[6] 徐文福, 刘厚德, 李成, 等. 双臂空间机器人捕获运动目标的自主路径规划 [J]. 机器人, 2012, 34(6): 704-714. [Xu Wen-fu, Liu Hou-de, Li Cheng, et al. Autonomous path planning of dual-arm space robot for capturing moving target [J]. Robot, 2012, 34(6): 704-714.]

[7] Siciliano B, Sciavicco L, Villani L, et al. Robotics: modelling, planning and control [M]. London: Springer-Verlag, 2009.

[8] Inaba N, Mitsushige O D A, Hayashi M. Visual servoing of space robot for autonomous satellite capture [J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2003, 46(153): 173-179.

[9] Yoshida K, Hashizume K, Abiko S. Zero reaction maneuver: flight validation with ETS-VII space robot and extension to kinematically redundant arm [C]. International Conference on Robotics and Automation, Seoul, Korea, May 21-26, 2001.

[10] 洪炳熔, 王鸿鹏. 双臂自由飞行空间机器人的姿态控制方案 [J]. 宇航学报, 2000, 21(2): 21-28. [Hong Bing-rong, Wang Hong-peng. Scheme of attitude control of dual-arm free-flying space robot [J]. Journal of Astronautics, 2000, 21(2): 21-28.]

[11] Hafez A H A, Mithun P, Anurag V V, et al. Reactionless visual servoing of a multi-arm space robot combined with other manipulation tasks [J]. Robotics and Autonomous Systems, 2017, 91: 1-10.

[12] Yoshida K. Practical coordination control between satellite attitude and manipulator reaction dynamics based on computed momentum concept[C]. Intelligent Robots and Systems, Munich, Germany, September 12-16, 1994.

[13] Mitsushige O. Motion control of the satellite mounted robot arm which assures satellite attitude stability [J]. Acta Astronautica, 1997, 41(11): 739-750.

[14] 徐文福, 李成, 梁斌, 等. 空间机器人捕获运动目标的协调规划与控制方法 [J]. 自动化学报, 2009, 35(9): 1216-1225. [Xu Wen-fu, Li Cheng, Liang Bin, et al. Coordinated planning and control method of space robot for capturing moving target [J]. Acta Automatic Sinica, 2009, 35(9): 1216-1225.]

[15] 徐文福, 周瑞兴, 孟得山. 空间机器人在轨更换ORU的力/位混合控制方法 [J]. 宇航学报, 2013, 34(10): 1353-1361. [Xu Wen-fu, Zhou Rui-xing, Meng De-shan. A hybrid force/position control method of space robot performing on-orbit ORU replacement [J]. Journal of Astronautics, 2013, 34(10): 1353-1361.]

[16] 袁景阳, 柳长安, 李瑰贤. 多臂协调操作自由飞行空间机器人的位置和内力混合控制 [J]. 宇航学报, 2007, 28(4): 1049-1052. [Yuan Jing-yang, Liu Chang-an, Li Gui-xian. Position and internal force hybrid control algorithm of multi-arm coordinated operate free flying space robot [J]. Journal of Astronautics, 2007, 28(4): 1049-1052.]