一种航天器星光折射连续导航方法

杨 博，苗 峻

(北京航空航天大学宇航学院，北京 100191)

0 引 言

利用星光折射间接敏感地平的导航方法是一种高精度的天文自主导航方法[1-3]，但在星敏感器接受折射光线的过程中必然会受到日、月、地等明亮天体的影响，相比于星敏感器正常捕获的星光亮度，太阳(视星等-26.78)、月球(视星等-12.7)、地气光光强都过强，这些杂光会造成星图背景增强，严重时甚至淹没星点目标，致使星敏感器测星任务失败[4]，这种观测缺失的现象即“星光空白段”，严重降低了航天器的导航精度和可靠性。

针对上述问题，现有的解决方法着重于两个方面：一是通过提高星敏感器制造工艺和结构设计水平，增加光学防护和信号处理防护，但仍难以满足杂光抑制要求[5]。二是使航天器在遇到干扰前禁止敏感器工作，干扰结束后恢复[6-7]。在此期间通过惯性导航系统或GPS导航系统进行辅助导航。其中，惯性导航系统虽然具有短时精度高的特点，但其导航定位误差随时间积累，难以长时间独立工作，初始对准时间较长，无法适应快速应用的场合；而GPS导航系统误差不随时间积累，但信号也容易受到干扰，尤其在航天器做机动时，容易丢失信息。

有学者提出研究飞行力学导航法(Flight dynamics navigation method，FDN)的软件补偿方法[8]，即利用最优估计理论估计出系统模型中的常值扰动误差及导航设备的误差源，并将其反馈回原系统校正，可以在不增加硬件设备的情况下明显改善导航性能，但该方法对轨道要求较高，并且只能针对常值的固有干扰有效，无法处理随机扰动。

神经网络具有联想记忆能力，能够不断学习存储信息，并对信息进行加工处理[9-10]。在航天器导航系统中，系统的状态误差修正与导航误差在时间序列中存在着非线性关系，利用神经网络的联想学习功能，将该时间序列关系转化成一个用非线性机制确定的输入输出系统，并建立系统输入和位置修正之间的权值网络，再对权值网络进行不断地学习训练，当在航天器受到日、月、地等天体干扰没有观测信息的“星光空白段”期间，利用训练好的权值网络迭代补偿航天器的位置信息，即可以低成本方法实现高精度的连续导航。

1 最优星光观测窗口

当折射星光穿过对流层时(折射高度小于20 km)，因对流层温度变化大、对流活动强烈，大气密度变化不稳定，间接敏感地平精度低。当星光折射高度大于50 km时，星光折射角过小，难以准确观测。20～50 km为平流层大气范围，其间温度变化缓慢，大气密度相对稳定，同一折射高度下的折射角基本恒定，是最佳利用星光折射间接敏感地平区间。

(1)

设u1为恒星星光恰好未在大气高度50 km处发生折射的临界星光矢量方向，由上述定义可得到上边界窗口角为：

(2)

式中：Re为地球半径，h1=50 km。

另设u2为恒星星光在大气高度20 km处恰好未发生折射的临界星光矢量方向，再由上述定义得到下边界窗口角为：

(3)

式中：α为星光在大气高度20 km时的折射角，h2=20 km。

由式(2)和式(3)可得到航天器获取经20～50 km平流层大气折射星光最佳观测窗口条件为：

φmin≤φ≤φmax

(4)

若某颗恒星满足该最佳星光观测窗口条件，即说明该恒星将在20～50 km高度间发生折射。

2 窗口星光观测模型

图2为航天器利用星光折射间接敏感地平的几何关系。其中：视高度为ha，实际折射高度为hg，星光折射角为R， 由图2几何关系可得

(5)

式中：u=|r·us|，r为航天器在历元J2000地心惯性系中位置矢量,r=|r|,us为未折射时星光在地心惯性系中方向矢量。Re为地球半径，a为小量，通常可被忽略。

由前期工作可得20～50 km范围内连续高度的星光折射角观测模型为：

R=0.0338exp(-0.1518026hg)

(6)

等式两边经过数学变换可以得到实际折射高度与折射角的函数关系为

hg=-22.3138-6.58750lnR

(7)

有密度随高度变化的模型

ρ=1537.3exp(-0.1462hg)

(8)

根据星光折射定律，折射高度hg与视高度ha的关系为[11-12]：

ha=hg+k(λ)ρ(Re+hg)

(9)

k(λ)为散射系数，由光波波长λ决定，ρ为hg处大气密度。λ=0.7 μm为星光的平均波长，k(λ)=2.2517×10-7为散射参数。

将式(7)和式(8)代入式(9)可得该区域内的视高度ha和折射角R的近似关系。航天器飞行过程中在最优折射窗口内量测到恒星折射角R，经式(9)计算得到相应的视高度ha，代入式(5)结合轨道动力学方程即可解算出航天器位置信息。

3 神经网络补偿星光空白段

航天器在轨飞行过程中，根据折射星光最优观测窗口条件实时选择导航折射星进行位置确定。当天体干扰等因素导致航天器无法观测到折射星进行导航，本文中将包括天体干扰在内的观测缺失的轨道段定义为“星光空白段”。

3.1 星光折射导航解算

选取航天器在地心惯性坐标系x,y,z三个方向的位置和速度为状态变量，即X=[xyzvxvyvz]T。

航天器动力学一步预测：

(10)

一步预测均方差:

(11)

估计均方差：

(12)

滤波增益：

(13)

一步状态误差修正：

(14)

一步位置估计：

(15)

导航误差：

(16)

式中:Dk为标称轨迹点。

3.2 神经网络引入

在上述导航解算步骤中，当没有观测量(即出现“星光空白段”)时，不能对一步位置估计值(式(15))进行修正，导航结果将发散。从时间序列来看，导航误差式(16)可以看作是一步状态误差修正的结果。分析发现它们之间隐含着非线性关系，将其时间序列关系转化成一个由非线性机制确定的输入输出系统，在该输入输出系统中引入神经网络。根据神经网络对信息有联想记忆的能力，不断从输入数据中提取特征，组织构造成最合适的权值网络，由此，获得系统输入输出之间的规律。系统在航天器飞行有观测时让神经网络学习规律获得训练，而在没有观测量(即星光空白段)时通过训练的网络来预测并修正航天器状态信息。

3.3 神经网络输入输出确定

对非线性时间序列相空间重构，建立如下结构矢量作为神经网络学习的输入：

(17)

矢量I首端为导航误差，中间为一步状态误差修正。

设第t+τ时刻状态误差修正信息可表示为：

δx(t+τ)=f(Δxt,δxt+1…,δxt+τ-1)

(18)

式中:τ为时间间隔。

输入误差空间重构为：

误差重构矩阵第i列元素表示为Ii。

构建神经网络期望输出矢量d为：

(19)

dk为d的第k列，表示航天器k时刻的一步状态误差修正。

由于频繁的网络训练会大大增加计算量，长时间积累后训练可能会导致过拟合现象。因此，本文采用每n=30间隔重新训练，依次更新网络。

3.4 神经网络方案设计

1)设计三层神经网络，输入层节点为30个，分别对应误差重构向量Ii，隐含层节点数在8～100，其目的是对输入层的数据进行相关映射，输出层节点1 个，对应误差修正信息。

将其网络最终输出表示成：

(20)

对于隐层，有：

yj=f(ψk),j=1,2,…,m

(21)

(22)

式中:yj为隐层第j个输出量，vij为对应Iij的权值，传输函数选择正切S型函数。

输出层第k个输出元素ok为：

ok=f(ψk),k=1,2,…,l

(23)

(24)

式中:wjk为对应yi权值，传输函数采用线性函数。对于航天器一组输入信息即可建立一组基本的权值连接信息和网络输出。

2)权值更新

当网络输出与期望输出不等时，定义输出误差为：

(25)

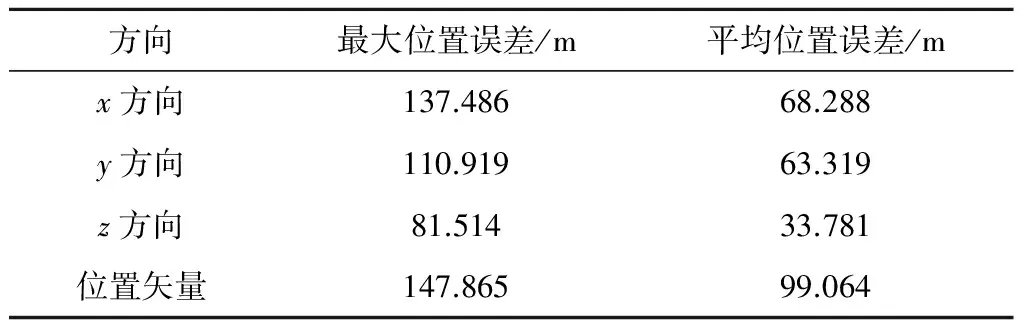
当E(n)

Δwjk=η(dk-ok)ok(1-ok)yj

(26)

(27)

式中:η为学习率，是一个常数，反映训练速率。本文采用自适应学习率：若经过一批次权值调整后E(t+1)误差减小，则本次调整有效，应该加速学习；如果经过一批次权值调整后E(t+1)增大，说明本次调整无效，应该放缓学习。

(28)

定义：

实际状态修正为有观测时的状态修正量，网络计算修正为有观测时通过神经网络计算出的状态修正量，这样就可以用学习相对误差来描述最终网络学习的优劣程度

3)保存权值网络

将步骤(2)最终修正得到的权值网络vij，wjk保存，当进入星光空白段时，将航天器在空白段初始位置的误差作为网络输入，求得航天器在空白段的一步状态误差修正值，之后将得到的一步状态误差修正值一并作为网络输入重复步骤(1)和步骤(2)进行导航解算。

航天器在飞行过程中，当有折射星被观测时，导航系统利用折射星光进行位置解算，同时建立即时神经网络权值；而当进入星光空白段时，导航系统通过神经网络补偿算法进行导航延续。在空白段初期，导航系统要根据空白段结束时刻标称轨道上的位置点，预测航天器飞出空白段的第一颗导航折射星方向，并依据该星光方向提前调整航天器姿态做好捕获准备。

4 仿真计算及分析

4.1 在轨“星光空白段”选取

仿真条件

1)航天器轨道：半长轴7136.635 km，偏心率e=1.809×10-3，轨道倾角i= 65°，升交点赤经Ω=30°,近地点辐角ω=30°，过近地点时刻t=0。

2)星光折射视高度量测噪声80 m，步长周期1 s。采用SKY2000 Version 2星库，恒星目视星等小于5.0 mag。

航天器动力学模型为：

(29)

式中：J2为地球带形谐系数，μ为地心引力常数，Δf为地球非球形摄动的高阶摄动项和日、月摄动以及太阳摄动、大气摄动等摄动产生的摄动力，Δfx， Δfy， Δfz分别为该摄动力作用到x,y,z轴上的分量。

选取如图3的一段为航天器飞行过程中的星光空白段进行分析。

图中坐标系为J2000地心赤道惯性坐标系。原点O在地球中心，平面xy与地球赤道平面重合。轴x指向春分点，轴z沿地球旋转轴(即垂直于赤道平面)，指向北极，空白段在标称轨道上起止坐标为图中标示。

图3中实线轨迹为航天器标称轨迹，其中加粗一段为以标称轨道为中轴扩展500 m观测区域。将该区域航天器位置代入第1节最优星光窗口条件分析，经星库筛选计算，发现星光观测窗口中不存在恒星，无法得到星光观测量，因此取该段为星光空白段。

根据不同具体任务背景，可通过提高动力学模型精度，建立更精确的空间环境模型，设计多神经网络结构复合，利用更深入的学习策略，可提高航天器在星光空白段的续航长度。一般地，考虑到学习效率和信息有效性，采用本文三层神经网络模型，空白段长度在学习间隔2倍以内效果最好。即空白段长度不应超过第3.3节训练飞行长度两倍(2n)为宜。

一般地，如果学习误差小于1%，其导航误差在10%内, 当学习误差大于1%时，需要进一步训练网络。

4.2 神经网络训练

进入星光空白段前训练的导航神经网络如图4所示。

图4、图5、图6分别为x,y,z三个方向的神经网络学习。其横轴为积累时间，竖轴为各方向上的位置状态修正，可以看到x方向学习相对误差为0.05573%，y方向学习相对误差为0.0896%，z方向学习相对误差为0.45%。同时可知，此时航天器已根据网络输入和期望输出得到了良好的三层神经网络权值，该权值能够有效提取网络输入信息，并通过映射计算得到期望输出。比较权值网络计算输出和折射星光导航解算输出，其结果非常吻合，说明网络学习是成功的，能够信赖的。

4.3 结果分析比较

可得神经网络学习迭代第一步输入：

定义：

将第一步输入代到第4.2节训练好的网络进行迭代，依次得到每一步状态修正值。基于第4.1节中含星光空白段的航天器标称轨迹(见图3)，导航系统利用神经网络在星光空白段续航，航天器实际飞行轨迹仿真结果如图7所示

从图7可以看出整个飞行轨迹连续性很好。星光空白段之前平均位置矢量误差(RMS)为99.064 m，星光空白段后平均位置矢量误差(RMS)为106.846 m。其精度相对误差为 7.86%，由此进一步说明，本文方法建立的权值修正网络能够基本保持原有的导航精度，完全可以实现航天器在星光空白段连续导航。

图8～图10分别为采用本文方法x,y,z方向上的导航位置误差，图11～图13为在空白段基于第4.1节动力学模型预估解算位置误差。表1所示为导航空白段前有观测时导航结果，空白段中采用两种方法导航结果如表2所示。

表1 空白段前有观测时导航结果Table 1 Navigation results obtained by observations

从表1和表2仿真结果的对比可以看出，采用神经网络补偿算法可以使星光空白段前后x,y,z三个方向上的位置误差波动均非常小，平均小于10%，因此有利于导航的连续性。

从表2可以看出，在导航空白段采用神经网络补偿算法比采用动力学模型导航解算将三个方向最大位置误差分别减少了44.50%，18.18%，35.68%，大大减少了波动，位置矢量平均位置误差减少了38.82%，提高了导航精度。可见，这种学习了空白段前的状态修正规律，并以此构建了修正网络进行导航补偿的方法，可以有效减小导航误差，实现精确连续导航。

5 结 论

星光折射导航在实际中应用具有很大的局限性，存在很多导航空白段。本文突破传统硬件限制，在不增加设备情况下，设计导航算法，解决了传统星光折射导航在无折射星段导航精度不高容易发散的问题，算法清晰明了，容易实现，具有独特的优势。主要结论如下：

1)导航折射星的确定：可以通过导航星观测窗口根据航天器位置分析可观测到的折射星。

2)位置状态修正与位置误差在时间状态空间中存在相关性，他们之间的关系是可以被神经网络学习表达的。

3)仿真结果表明,神经网络预测导航算法具有较高的导航精度，合方向精度误差在10%之内，各个分方向也达到了良好的精度，各个方向最大位置误差幅值在10%之内，算法可以实现高精度导航。

[1] 宁晓琳, 王龙华, 白鑫贝．一种星光折射卫星自主导航系统方案设计[J]. 宇航学报, 2012, 33(11): 1601-1610. [Ning Xiao-lin, Wang Long-hua, Bai Xin-bei, et al. A scheme design of satellite autonomous navigation system based on stellar refraction [J]. Journal of Astronautics, 2012, 33(11): 1601-1610.]

[2] 杨博, 陈子匀, 刘孝孝, 等．一种基于LPF + POD 的星光导航气动光学效应研究方法[J]. 宇航学报， 2016, 37( 1) : 74-83．[Yang Bo, Chen Zi-yun, Liu Xiao-xiao, et al. An LPF +POD based method to study aero-optical effect of starlight navigation [J]. Journal of Astronautics, 2016, 37 (1): 74-83.]

[3] 杨博, 俞雪瑶, 苗峻. 一种利用地球敏感器的星光导航方法[J]. 宇航学报, 2016, 37(9):1089-1097. [Yang Bo, Yu Xue-yao, Miao Jun. A method of starlight navigation using the infrared horizon sensor [J]. Journal of Astronautics, 2016, 37(9):1089-1097.]

[4] Rulino F. Enhancement of the centroiding algorithm for star tracker measure reflinement [J]. Actastronautica, 2003, 53:135-147.

[5] Liebe C C. Accuracy performance of star trackers a tutorial[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2):587-589

[6] Gueymard C A. The Sun’s total and special irradiance for solar energy applications and solar radiation models [J]. Solar Energy, 2004, 76(4):423 453

[7] Zong Y, Brown S W, Meister G, et al. Characterization and correction of stray light in optical instruments[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2007, 16(3):313-323.

[8] 柴霖, 袁建平, 方群. 飞行力学导航法探讨[J]. 导弹与航天运载技术, 2003(1):12-18. [ Chai Lin, Yuan Jian-ping, Fang Qun. Study on flight dynamics navigation method [J]. Missiles and Space Vehicles, 2003(1):12-18.]

[9] 禹建丽, 卞帅. 基于BP神经网络的变压器故障诊断模型[J]. 系统仿真学报, 2014, 26(6):1343-1349. [ Yu Jian-li, Bian Shuai, Fault diagnosis model of transformer based on BP neural network [J]. Journal of System Simulation,2014, 26(6):1343-1349.]

[10] 焦李成, 杨淑媛, 刘芳,等. 神经网络七十年:回顾与展望[J]. 计算机学报, 2016, 39(8):1697-1716. [Seven years beyond neural networks: retrospect and prospect [J]. Chinese Journal of Computers, 2016, 39(8):1697-1716.]

[11] Wang X L, Ma S. A celestial analytic positioning method by stellar horizon atmospheric refraction [J]. Chinese Journal of Aeronautics, 2009, 22(3): 293-300.

[12] Yang B, Si F, Xu F, et al. Adaptive measurement model of navigation by stellar refraction based on multiple models switching [J]. Journal of Navigation, 2014, 67(4): 673-685.