铁路空车调整优化模型研究

于 横，温 鑫 YU Heng,WEN Xin

（1.呼和浩特铁路局呼和货运中心，内蒙古 呼和浩特 010000；2.呼和浩特铁路局集宁站，内蒙古 乌兰察布 012000）

0 引言

铁路空车调整问题是涉及铁路运输资源优化配置的重要问题，“不仅是实际生产中的重要内容”，同时也是国内外很多学者研究的热点问题[1]。

车流调整是铁路调度工作的一项重要内容，在日常运输组织工作中，车流调整通过合理的车流预测、推算、组织，防止区间通过能力浪费和线路、车站阶段性堵塞[2]。车流调整必须实行高度集中、统一调整的原则[3]。在货物运输过程中，空车资源是装车的保证，空车又来源于重车的卸车作业[4]。铁路空车产生于卸车量大于装车量的车站，即空车供给站。然而，铁路货流的始发位于空车需求站。铁路路网上空车需求站与空车供给站的分布通常并不均衡，有些车站只能产生空车，并没有货源，而有些车站则相反，还有部分车站既是空车的供给站，又是货流的始发站。因此，需要将空车供给站（卸车站）产生的空车源源不断地运送至空车需求站（装车站），即空车调整。

随着我国经济社会进入转型阶段，铁路过去以煤炭、钢铁为主的货运需求大幅下降，在此大背景之下，我国铁路货运部门进行了一系列以市场为中心的货运组织改革。其中，对于铁路车流组织的优化是铁路部门以市场为中心改革的重要内容之一。空车调整又是车流组织中的主要组成部分，也是铁路车辆资源合理运用的重要手段[5]。

在我国铁路货车中敞车约占了60%以上的比重，并承担了大部分货种的装运任务[8]，但是，高效的空车调整计划可以进一步缓解空车供给需求紧张的矛盾，对铁路部门提质增效具有正面的促进作用。

1 铁路空车调整优化模型的建立

在当下铁路货运组织改革的背景下，应将市场的要素更多地考虑其中，所以本文在模型建立的过程中分别将车种代用要素，装车站最优空车装车时间窗要素考虑在内，最后为了更加契合市场要素，将目标函数设置为空车调整后铁路部门营业收入最大化。

模型参数及变量如下：

模型共有6个约束条件，分别是节点车流平衡约束、空车车流直达约束、货运计划约束、铁路货车保有量约束、空车供给能力约束、决策变量取整约束。下面分别对前5个约束条件进行进一步说明。

节点车流平衡约束。对于铁路路网上的任意一个节点，其到达的车流中包含有到达空车流与到达重车流。同理，节点出发的车流中包含出发空车流与出发重车流。其到达的货车数应与出发的货车数在数量上相等，见图1。

所以，对于路网中任意节点有以下车流平衡约束：

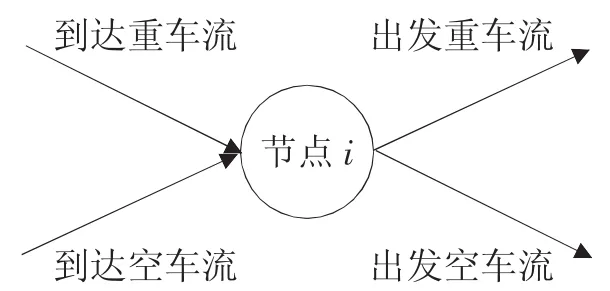
图1 节点i车流构成

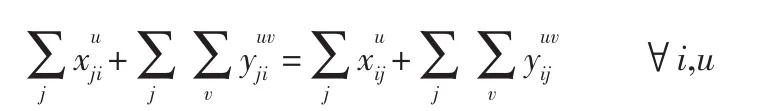
空车车流直达约束。设置该约束的目的是为了避免空车车辆的循环走行和多余走行，限制空车能够一次调配到位，所以对于空车车流有以下约束：

（3）评标不公正、不科学；询标不公正，对关系户只提优点，不提缺点，对其他竞争对手只提缺点，突出关系户各方面都优于其他竞争对手；评标过程不公开；定标前谈判压价和违规分包，定标后在签合同时还要过分压价；

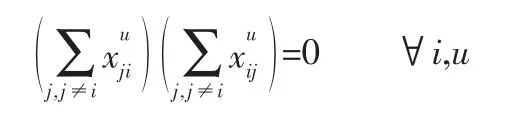
货运计划约束。对于重车车流，装运的货物首先应满足每日总公司的指令性任务。所以有以下约束：

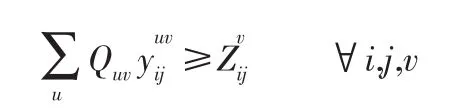
其次重车车流在满足指令性任务的基础上，应尽量满足货物运输计划中的其它运输任务。所以有以下约束：

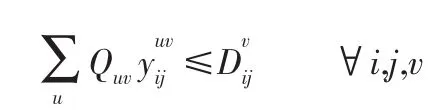
铁路货车保有量约束。货车保有量对于货车利用有很大影响。为了持续不间断地完成运输任务，铁路局都要有一定数量的货车保有量：

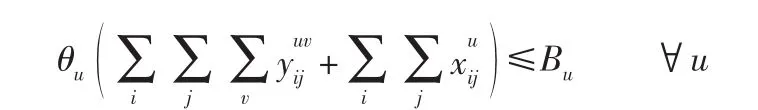
车站空车供给能力约束。对于空车供给站i所能提供的空车不应大于其自身的供给能力A供i：

模型目标函数考虑铁路部门营业收入最大化，其中考虑了下列要素：重车所获得的收入部分、调运空车所花费的费用部分、车种代用策略所花费的费用部分、货运需求没有得到满足造成的损失部分、考虑装车站空车需求时间窗所需费用部分。接下来对模型目标函数的各个部分进行进一步解释说明。

重车收入部分，重车收入是铁路部门的主要收入来源，该要素与各站间各品类货物的运价、货车静载重和铁路部门装车的重车数有关。目标函数中重车收入部分可表示如下：

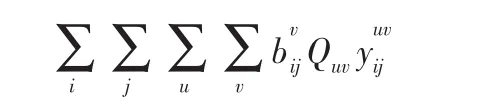
调运空车费用部分。对于某卸车站卸空的某种车种的货车，在满足本站双重作业车后，仍有多余的货车车辆，要向需要该种车种的装车站调配，在调配的过程中会产生空车调整费用。该部分费用与各货运站间的空车调运费用和空车车数有关。目标函数中空车调整费用部分表示如下：

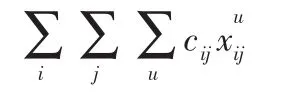
车种代用费用部分。在运输生产的实际过程中，通常会出现某种或某几种货车车种相对短缺而其它车种数量相对富余的状态，针对这样的情况，车种代用成为运输生产过程中一种必要的手段。但是采用车种代用策略由于代用之后的装载加固、加装篷布等会产生车种代用费用。铁路部门车种代用费用表示如下：

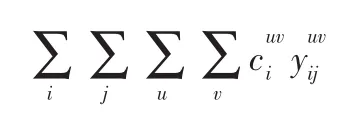
未被满足的货运需求所造成的损失。与运输需求相比，铁路某些货车车辆资源属于相对短缺资源。货主向铁路运输企业提报的请求车计划不可能全部满足。此时，铁路运输企业并未满足的运输需求的状况相比于满足该部分货运需求时造成了损失。为简化模型，将未被满足的运输需求对铁路运输企业所造成的损失近似看作货物的运价部分。该部分在目标函数中表示如下：

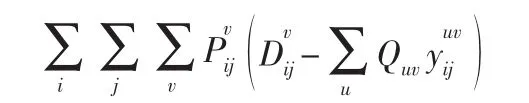
当重车全部到达目的地卸车为空车后，需要向空车需求站进行空车的排空。然而，在现实情况下一日中装车站对于各类空车的需求有一个时间窗的约束，即该装车站对于某种货物的装车需要在一个时段内，若空车提前到达则会在该站进行存储，从而产生空车存储费用；若空车延迟到达货物则会继续占用仓库从而产生额外的仓储费用；只有当空车到达时间在一定的时间段内不会产生以上所描述的费用。所以，对于本文空车调整模型引入空车需求时间窗要素，该要素有两项构成分别是空车提前到达的空车存车费用和空车延误到达的货物仓储费用，表示如下：

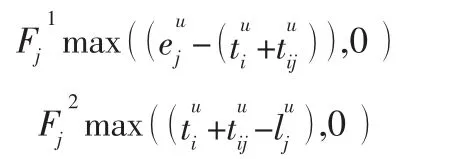
将上述目标函数各项与约束条件结合起来，构成考虑铁路运输企业营业收入最大化的铁路空车调整计划优化模型：

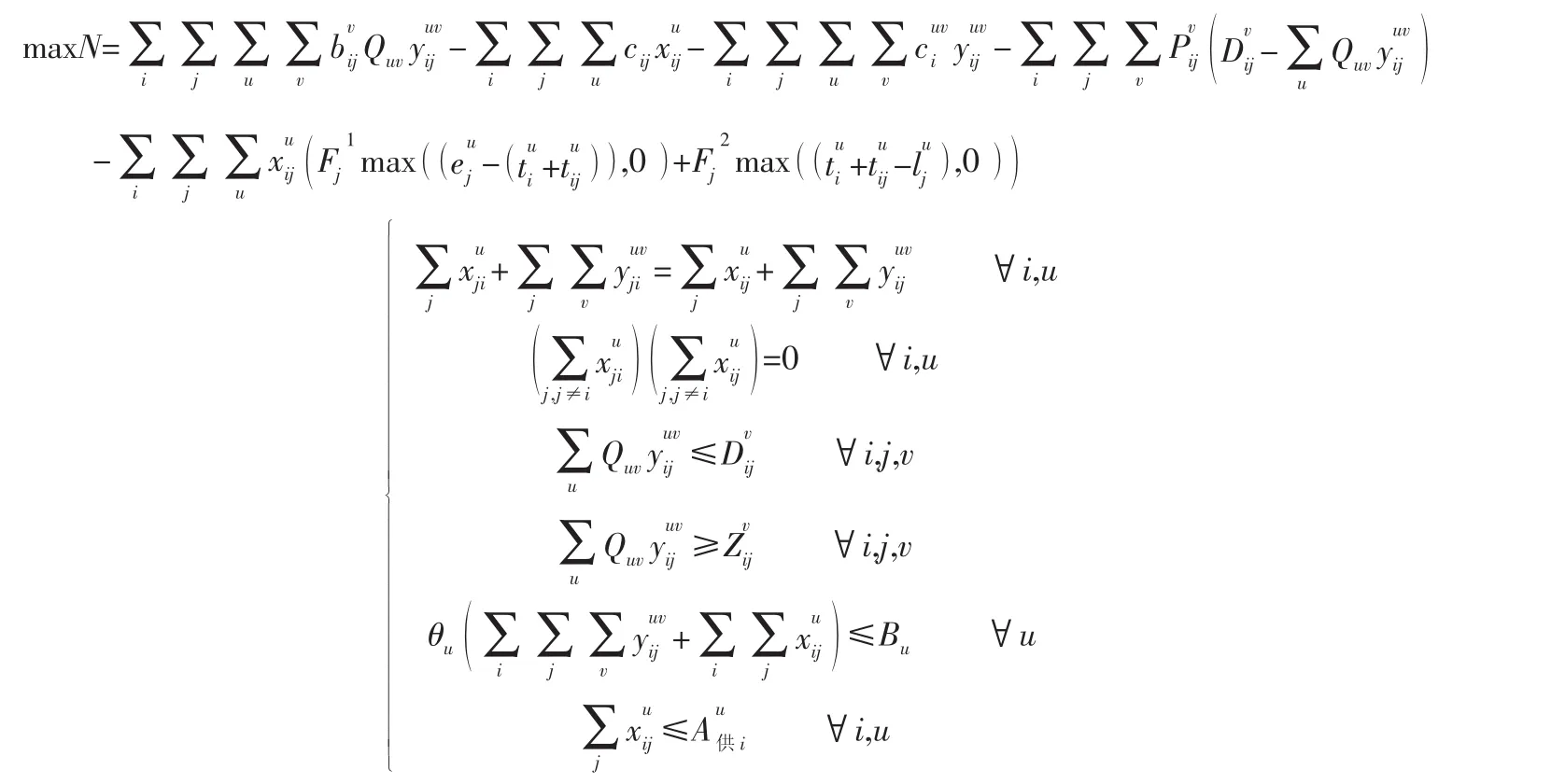
2 结 论

本文提出了在节点车流平衡约束、空车车流直达约束、货运计划约束、铁路货车保有量约束、车站空车供给能力约束的条件下，并考虑车种代用因素与装车站空车需求时间窗因素，将目标函数设置为路局营业收入最大化。从而能够进一步适应铁路以市场为中心的货运组织改革，节省运输成本，提高运输效益。对提高铁路货运部门服务质量与服务水平都有积极地促进作用。

[1] 张红斌，董宝田，孙远运.基于能力约束的多车种空车动态调整方法[J].北京交通大学学报，2016,40(6):50-56.

[2] 曲思源.不均衡运输条件下车流调整的优化[J].铁道运输与经济，2007,29(2):41-53.

[3] 铁道部.铁路运输调度规则[Z].2005.

[4] 谭云江.路网节点间空车调配模型与算法研究[D].成都：西南交通大学（硕士学位论文），2006.

[5] 王都，闫海峰，谭云江.路网节点间铁路冷藏车空车调整的蚁群算法[J].中国铁道科学，2008,29(2):131-135.

[6] Paolo Toth,Daniele Vigo.An Overview of Vehicle Routing Problems[C]//The vehicle routing problem,2002:1-26.

[7] 铁道部科学技术研究所.国外铁路[Z].1991.

[8] 王占国，何莹.我国铁路敞车运用[J].中国铁路，1999(12):35-36.