基于中断不确定的最可靠配送路径选择研究
孙仕豪,樊相宇,武小平 SUN Shihao,FAN Xiangyu,WU Xiaoping
(西安邮电大学 现代邮政学院,陕西 西安 710061)
0 引言
快递服务中,快递配送是与客户直接接触的终端服务。配送能否完成是快递服务最基本条件。配送路线的可靠性是决定配送服务能否准时完成的先决条件。黄建华等[1]强调,快递行业与其他行业有所不同的是,快递行业不同时要求成本与效率同时最优,而是以承诺的服务时间为效率最优目标,即在效率方面只是要求快递行业在承诺的服务时间范围内为客户完成快递服务。设计了一套配送路线、配送成本、配送方式等都与时间阈有关的快递路线设计方式。杨从平等[2]则进一步在最短路算法的基础上,再对边介数、节点介数进行加权求和得出快递网络边的货物流量和节点的货物中转量进行约束。构建带有配送时间约束和节点最大流量约束的快递网络优化模型。
学者关于配送路线流量的算法,主要有遗传算法、神经网络、分层理论、灰色关联模型等,这些算法都是在历史数据基础上进行的。由于配送路线上的社会车流量很难准确测量,且快递配送网络出现时间较晚、历史数据不足,导致从问题抽象出图的模型时,会将不精确信息反映在图中。很多情况下,不精确信息表现为专家经验数据的形式,可以借助不确定理论来进一步解决此类问题。刘宝碇[3]建立了不确定理论,提出了不确定测度,它是一个满足规范性、对偶性、次可列可加性、乘积公理的集函数。高原等[4]应用不确定理论于网络中,给出了不确定图的定义和相关概念,并证明了不确定图中常用的定理。接着从边数、边连通度和直径等基本性质展开对不确定图的研究。边数在不确定图中是一个不确定变量,给出了它的分布函数和期望,形成不确定网络。Han S等[5]在不确定网络的基础上,提出了不确定网络的最大流函数的概念,运用不确定理论研究了不确定网络的最大流问题,给出了不确定网络最大流的不确定分布。
配送路线可靠性[6]的研究大致分为基本可靠性和任务可靠性的研究。配送基本可靠性是从路径的存在和数量来研究网络传输流的能力,配送路线基本可靠性的度量测度包括路线的抗毁性和生存性,是基于路线连通的确定性测度和概率性测度。因此配送路线可靠性的测度对象都是可得到确定性测度的配送货物或配送车辆。本文引入了不确定理论,配送路线可靠性的测度可变为不确定测度,研究配送路线的测度对象就可选择社会车流量,建立一个更符合实际情况的快递配送网络最可靠路线模型。
1 问题描述与相关理论
关于不确定网络模型的研究大多都是对普通网络,未结合实际情况进行条件约束。本文以快递网络为背景,在不确定网络的基础上,以配送路线中断为不确定测度、社会车流量为不确定流,结合各快递网络自身结构特点,构建中断情形不确定的最可靠配送路线模型。
1.1 问题描述
已知配送网络的起点s、终点t,所有配送路线vn的车容量c确定,所有配送路线上的社会车流量w不确定。任意配送路线的社会车流量与该路线的中断程度都成正比,社会车流量越多,配送路线中断的可能性越大。因为配送路线上的社会车辆w不确定,所以不能准确知道各配送路线的中断情况p,进而不能确定选择的配送路线是否会中断。本文以配送路线出现中断可能性最小为目标,在配送网络的社会车流量最大时,选择一条出现中断可能性最小的路线作为最可靠配送路线,并给出该配送路线的社会车流量。
1.2 相关理论
Liu B[3]提出不确定测度的定义、不确定分布定义:
定义1 M是一个不确定测度,那么对于任意事件Λ,有0≤M{Λ }≤1。
定义2 对于不确定变量ξ,它的不确定分布Φ定义为Φ(x)=M { ξ≤ x },∀x∈R。
Liu W[7]提出不确定网络的定义:
定义3 网络N=(V,E, )W 中,如果权重W为不确定变量,那么该网络称为不确定网络。
刘宝碇在文献[3]中提出E-99最大流法则,不确定分布Φ(x)中的不确定变量n可用E-99表表示。
定理1[8]如果网络N=(V,A,w,s,t)存在不确定分布Φij,(i,j)∈A。那么网络N最大流就是N'=(V,A,C,s,t)确定网络的最大流,此时弧的容量为其反函数为
定理2[9]网络G是一个有n个弧的不确定网络,f( w1, w2,…,wn)是网络G的最大流函数,此时f( w1, w2,…,wn)是一个关于wi的连续单调递增的函数,wi表示第i个弧的不确定分布的权重,i=1,2,…,n。
定理3[9]网络G是一个有n个弧的不确定网络,f( w1, w2,…,wn)是网络G的最大流函数,那么不确定网络G的最大流函数f就是一个不确定变量ξ,其逆不确定值为:

此时εi表示第i个弧的不确定分布的权重,i=1,2,…,n。
定理4[9]网络G是一个有n个弧的不确定网络,f( c1,c2,…,cn)是网络G的最大流函数,εi表示不确定分布Φi(x),i=1,2,…,n 中第 i个弧的不确定权重。那么最大流 ε=f( ε1,ε2,…,εn)存在一个期望值dα。
定理5[3]网络G是一个有n个弧的不确定网络,f( c ,c ,…,c)是网络G的最大流函数,ε表示不确定分布Φ (x),i
12nii=1,2,…,n中第i个弧的不确定权重。如果Ψ(x)是一个由E-99方法得到的最大流为ε不确定分布,那么最大流ε=f(ε1,ε2,…,εn)的期望值为当且仅当i=1,2,…,99。
2 模型建立
设快递网络为N=(V,A,w,s,t),本文用w为不确定变量(由不确定测度p表示配送路线的中断程度。当p=0时,表示该路径通畅状态;当p=1时,表示该路径为堵塞状态),表示配送路线的车流量,V表示配送网络的点集,A表示配送网络的弧集。弧的大小表示配送路线的流量容量。在此基础上,利用配送网络自身结构特点,计算每条配送路线的容量介数b。其意义与边介数相同,都表示该路线在整个网络中作用与影响力。数值越高,该配送路线越不可靠。定义容量权数:
配送路线的车流量容量a在配送网络拥堵时使该配送路线中出现中断的可能性。
设网络的路线中断—车流量不确定分布函数为Φi(p),由于路线中断与车流量成正比例关系,因此可以引用不确定理论[8]中的线性函数公式,设网络的路线中断—流量函数为:

应用定理1得到:
Φ wi()=p的反函数为:

设该快递网络的最拥堵车流函数为f( w1, w2,…,wn),根据定理1~3可得网络的逆不确定最拥堵流值为Ψ-1(p)=f
刘宝碇在文献[3]中提出E-99最大流法则,不确定分布Φ(x)中的不确定变量n的不确定最大流可用E-99表表示。
过程如下:
(1)确定网络结构,确认发件地s、收件地t以及所有可能经过的节点vi、弧ai。
(2)给出每一条配送路线上可能出现的社会车流量w的范围以及配送路线中断p的判断标准。
(3) 建立配送路线中断—车流量Φ( wi)(式1) 以及其反函数Φ-1(wi)(式2)。
(4) 建立快递网络的最拥堵车流函数f( w1, w2,…,wn)与其反函数
(5)利用E-99最大流法则,对不配送路线中断程度进行细分,p=0.01至p=0.99,再利用Fold-Fulkerson算法得到对应中断的最大拥堵流值Ψ-1()p,得到E-99最大流表。
(6)利用定理对E-99表进行验证。
此时可以得到关于该配送网络的路线中断—车流量二维图,由该图可以求得任意中断程度的最大车流量。
由E-99表可以得到各配送路线不同中断程度的最大拥堵车流矩阵W,由配送网络得到该网络的容量介数矩阵B。结合Busacker-Gowan算法,得到不同最大社会车流量中出现最小中断可能性的社会车辆流,即为不同中断程度的最可靠配送可行流。
过程如下:
(1)选择可能的中断程度p,利用E-99遍得到对应的配送网络流量矩阵W。
(2)已知配送网络结构与各配送边的流量容量,得到配送网络的容量介数矩阵B。
(3) 借助 Busacker-Gowan[10]算法:
设网络G( V,E, )C ,取初始可行流f为零流:
①构造有向赋权图Gf=(V,Ef,)F ,对于任意的vivj∈E,Ef和F的定义如下:
ⅰ. 当 fij=0 时,vivj∈Ef,F( vivj)=bij;
ⅱ. 当 fij=Cij,vivj∈Ef,F( vivj)=-bij;
ⅲ. 当 0<fij<Cij,vivj∈Ef,F( vivj)=bij。
②求出有向赋权图Gf=(V,Ef,)F 中发点vs到收点vt的最短路μ,若最短路μ存在,则转向③;
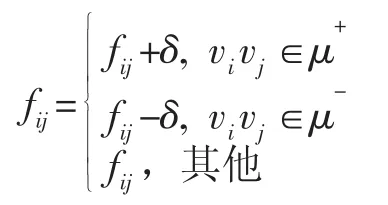
若所得的最大流量Wf大于或等于预定的流量值,则适当减少δ值,使Wf等于预定的流量值,故f就是所求的路线中断可能性最小的车辆流,停止;否则转向①。
转化为线性规划描述如下:

设fmax为最大流,若v(f)=v( fmax),则就是该问题的解;若v(f )>v( fmax),则无解。
(4)代入W与B矩阵,求得最可靠配送可行流F矩阵。
(5)由该矩阵得该中断程度的最可靠配送路线。
3 算例分析
根据《城市区域环境振动标准》 (GB10070-88)中的“交通干线道路”是指平均车流量每小时100辆以上的道路。因为配送一般都为单向配送,所以设配送路线的平均车流量标准为每小时50辆以上的道路。设配送路线的车流量容量为配送路线路程与平均车流量的乘积。若不超过该道路车流量容量一半为畅通,P=0;若超过车流量流量的1.5倍则为堵塞。配送路长用l(km) 表示,l1=10、l2=8、l3=7、l4=5、l5=2、l6=4、l7=9、l8=11,配送路线的车流量容量为a1=500、a2=400、a3=350、a4=250、a5=100、a6=200、a7=450、a8=550。路径的交通流量为w1=(250~750 )、w2=(200~600 )、w3(175~525 )、w4(125~375 )、w5(100~300 )、w6(50~25 0 )、w7(225~425 )、w8(275~475 )。利用公式1、定理、E-99算法,得到E-99表与路线中断—车流量如表1、图1、图2。

表1
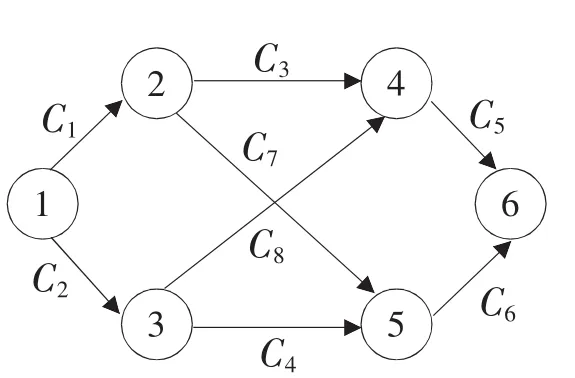
图1

图2
再根据定理,求得期望值E()p≈689,p≈0.51在估值范围之内,验证该不确定分布可接受。
通过各配送路线的流量容量计算出各边的容量介数,由MATLAB运算得b1=0.2,b2=0.3,b3=0.15,b4=0.25,b5=0.45,b6=0.45,b7=0.3,b8=0.2。则该配送网络的容量介数矩阵为:

若选择期望值下的最优路线,则配送网络的流量矩阵为WP=0.51:

由Busacker-Gowan算法求得p=0.51时的最可靠最拥堵流F的矩阵F为:

由该可行流可得到具体的配送路线:1→2→5→6。
4 结论与展望
快递企业在选择快递配送路线时,都以准时安全送达为基本要求。配送路线为配送任务完成的基础条件,其可靠性是快递业务完成的保证。关于快递配送路线的可靠性研究,主要集中于指标确定的配送路线选择,以及该配送路线服务水平与服务能力的评估。在考虑实际动态变化的方面,还有待于深入研究。本文基于不确定理论,以配送路线上的交通流量为不确定变量,结合边介数与Fold-Fulkerson、Busacker-Gowan算法,形成一套不确定网络的可靠性路线选择模型。该模型有三方面优点:(1)不确定理论,更切合实际,使网络适用于配送实际情况。(2)模型中的参数与数据,可根据实际情况进行调整,实用性更高。(3)Busacker-Gowan算法在一方面考虑社会车流量最大值的同时,也考虑了出现最少中断的要求,更符合实际快递配送设计要求。本文仍有未讨论的方面,如:只考虑了道路流量,未考虑节点的各类情况,该方面需要进一步的补充与研究。
[1] 黄建华,党延忠.具有社区结构和子核的快递网络优化方法[J].系统工程理论与实践,2014(11):2826-2836.
[2] 杨从平,郑世珏,党永杰,等.基于配送时间及节点流量约束的快递网络优化[J].系统工程,2015,11:53-59.
[3] Liu B.Uncertainty Theory[M].2版.Berlin:Springer-Verlag,2007.
[4] 高原.不确定图与不确定网络[D].北京:清华大学(博士学位论文),2013:30-31.
[5] Han S,Peng Z,Wang S.The Maximum Flow Problem of Uncertain Network[J].Information Sciences,2014,265:167-175.
[6] 黄宁,伍志韬.网络可靠性评估模型与算法综述[J].系统工程与电子技术,2013(12):2651-2660.
[7] Liu W.Uncertain Programming Models for Shortest Path Problem with Uncertain Arc Lengths[C]//Proceedings of the First International Conference on Uncertainty Theory,Urumchi,China,2010:148-153.
[8] Han S,Peng Z,Wang S.The Maximum Flow Problem of Uncertain Network[J].Information Sciences,2014,265:167-175.
[9] Ding S.The α-Maximum Flow Model with Uncertain Capacities[J].Applied Mathematical Modelling,2015,2(7):2056-2063.
[10]王海英,黄强.图论算法以及MATLAB实现[M].北京:北京航空航天大学出版社,2010:44-46,77-78.

