基于优选码相位的扩频水声通信系统
于 洋,张 柯,孟耀伟,孙宗鑫
(1.许昌学院 交通运输学院,河南 许昌 461000;2.许昌学院 信息工程学院,河南 许昌 461000;3.哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001)
水声通信由于其传输介质是海水而使其有别于无线电通信,由于海水介质和空气介质的不同,也使水声通信展现出许多不同的特性.由于声音在海水中的传输速度较低,衰减较大,有效可利用的带宽较窄,使水声信道成为最具挑战性的信道之一[1,2].
扩频水声通信由于其良好的抗噪声,抗衰落和抵御有意和无意的干扰能力而被广泛应用于中远程水声通信[3],隐蔽通信[4],鲁棒水声通信.由于扩频通信具有一定的多址接入能力,还使其在水声通信网中得到了重要的应用[5,6].传统的扩频水声通信分为直接序列扩频(DSSS)和跳频扩频(FHSS),它们都在水声通信领域得到了应用.FHSS更适合快衰落信道,而DSSS则更适合频率选择性衰落[7].随着研究的深入,许多致力于提高传统水声通信性能,通信速率和作用距离的算法被研究[8-10].
对于扩频水声通信来说,序列是决定系统性能的重要因素,它的相关特性决定了系统的多址接入能力和抗多径衰落的能力.传统的扩频通信采用m序列作为DSSS系统常用的序列.本文也将以m序列为例,研究其不同的码相位下在时域扩频和频域扩频两种情况下对水声通信系统性能的影响.对于时域扩频水声通信系统,误码率性能(BER)将作为一个衡量的标准,而对于频域扩频水声通信系统,BER和峰均功率比(PAPR)这两个参数都将作为系统衡量的标准.
1 原理
1.1 时域扩频水声通信系统
基于时域扩频的水声通信系统的发射信号可以表示为
s(t)=Ab(t)c(t)cos(ωct+φ),
(1)
其中,b为数据信息,c为扩频码,信号的幅度为A.经过水声信道,信号可以表示为
(2)
其中,直达信号的传播时延为τ0,衰减后的幅度为A0.
多径信号的传播时延为τl,幅度为Al,1≤l≤L,其中L为多径的数目.信号经过处理,并忽略频率的高次项,每符号的积分输出可以表示为
(3)
从上式可以看出,等式右端第一项是期望的结果,第二项是多径衰落的影响,第三项是噪声.L表示的是能影响到此符号输出的多径数目.可以看出,序列的相关函数是影响系统性能的一个重要因素.下面就对该影响在码片级别上进行分析:
周期自相关函数(PACF)可以表示为
(4)
上式中,N代表序列的长度.部分相关函数可以表示成为以下的形式:
(5)
还可以表示为
(6)
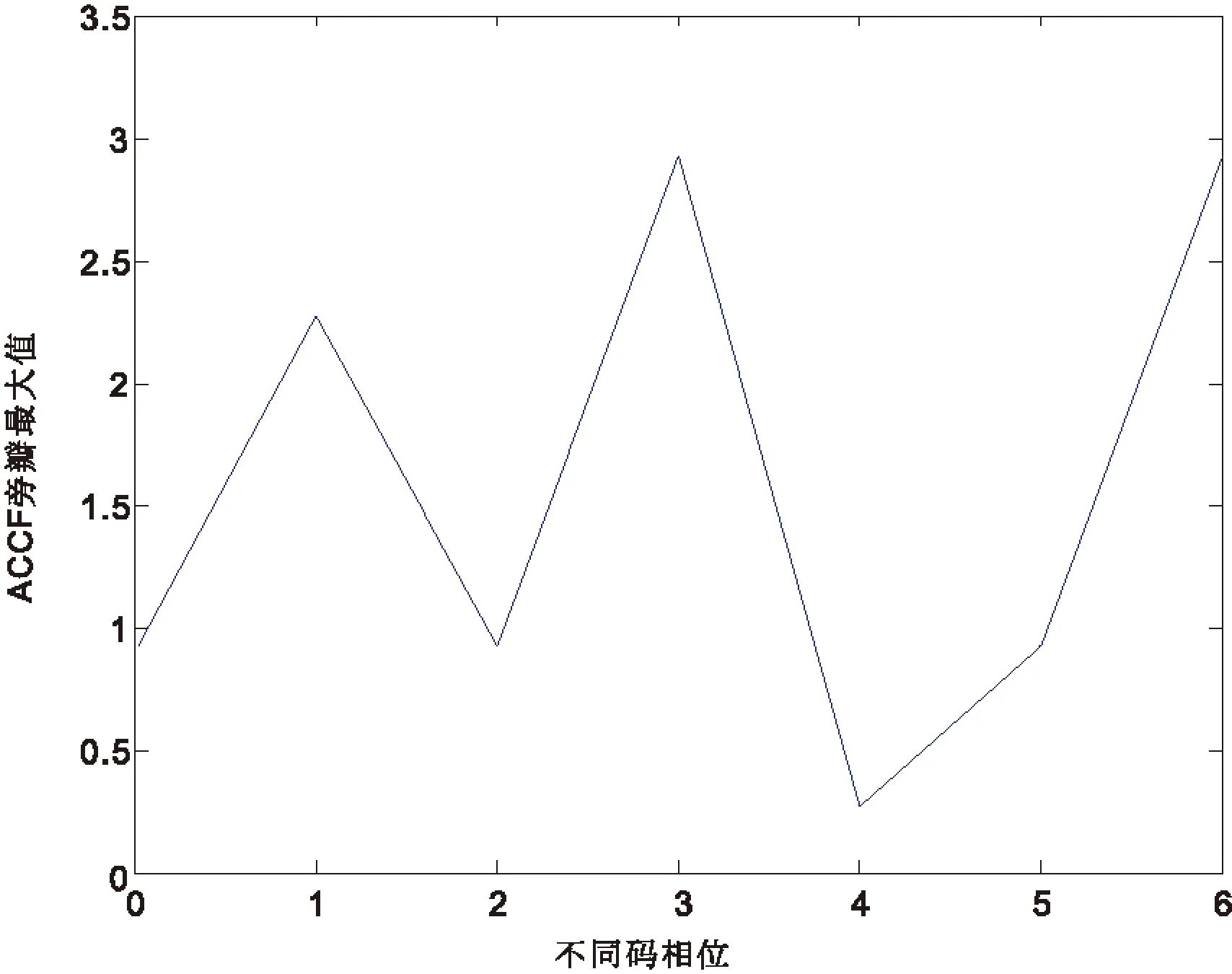
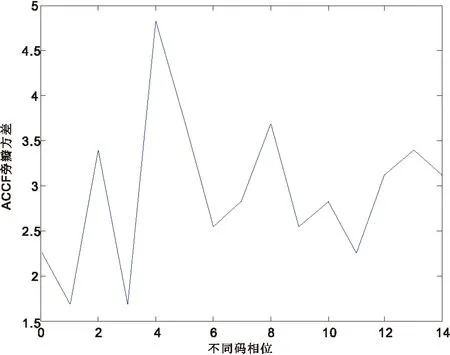
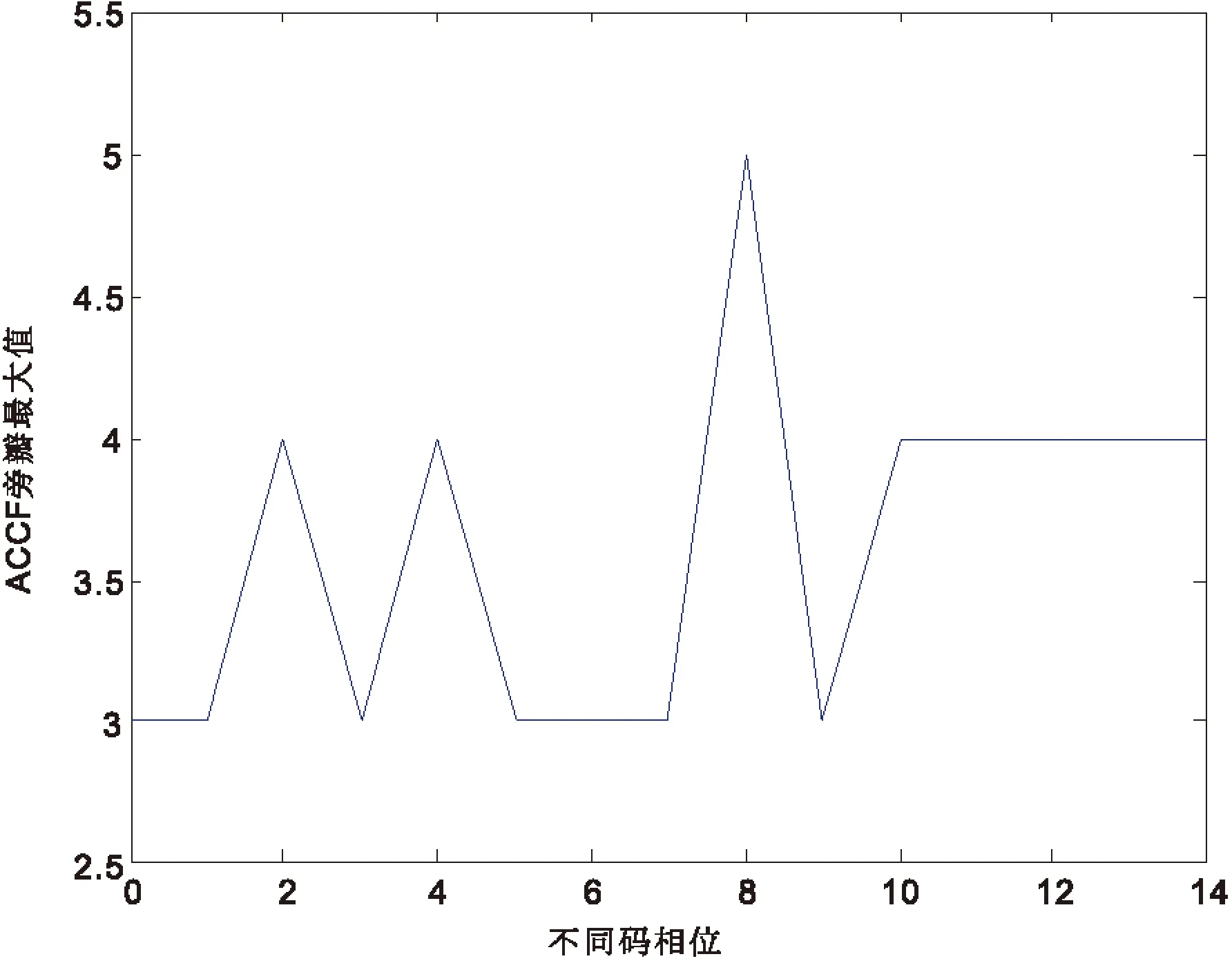
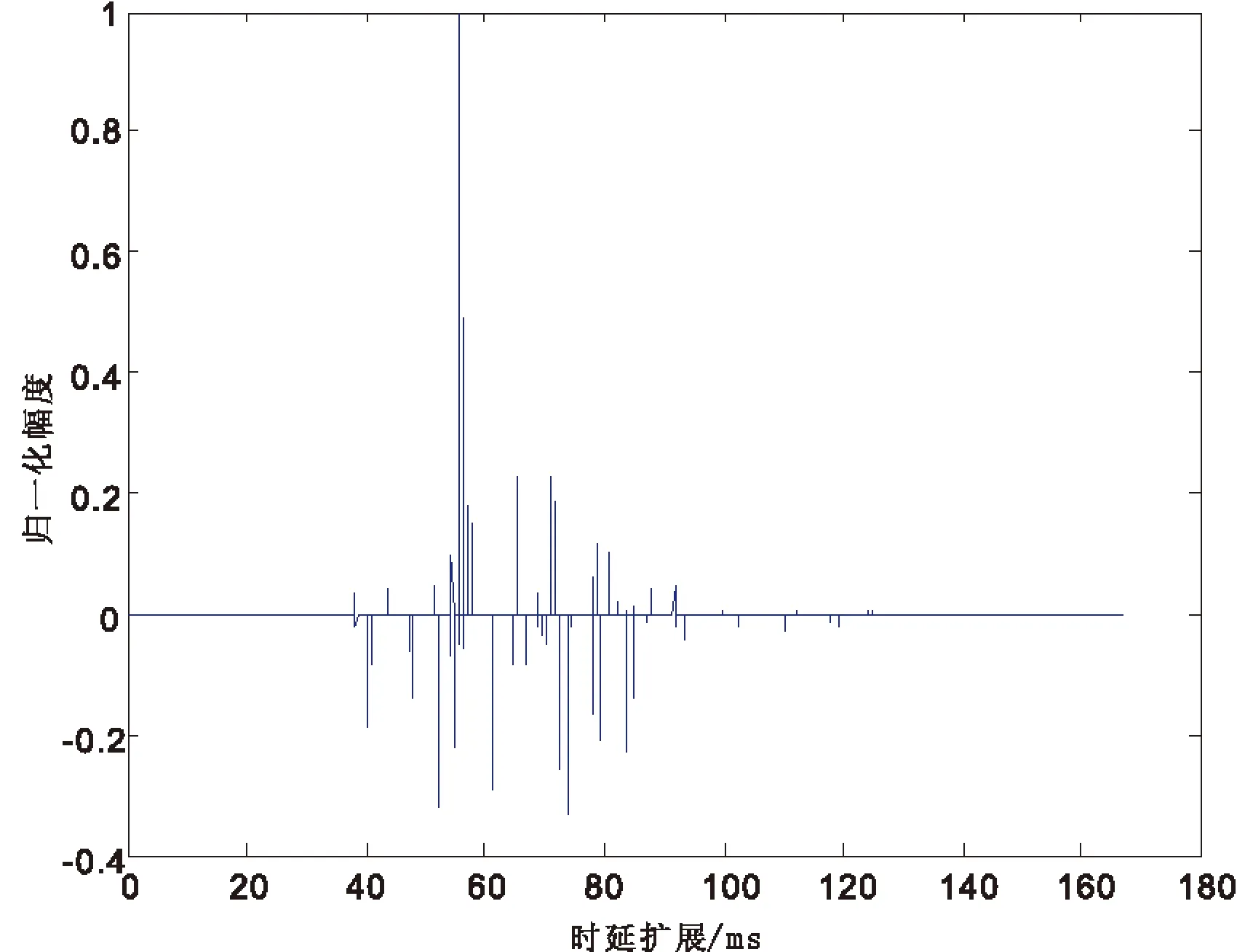
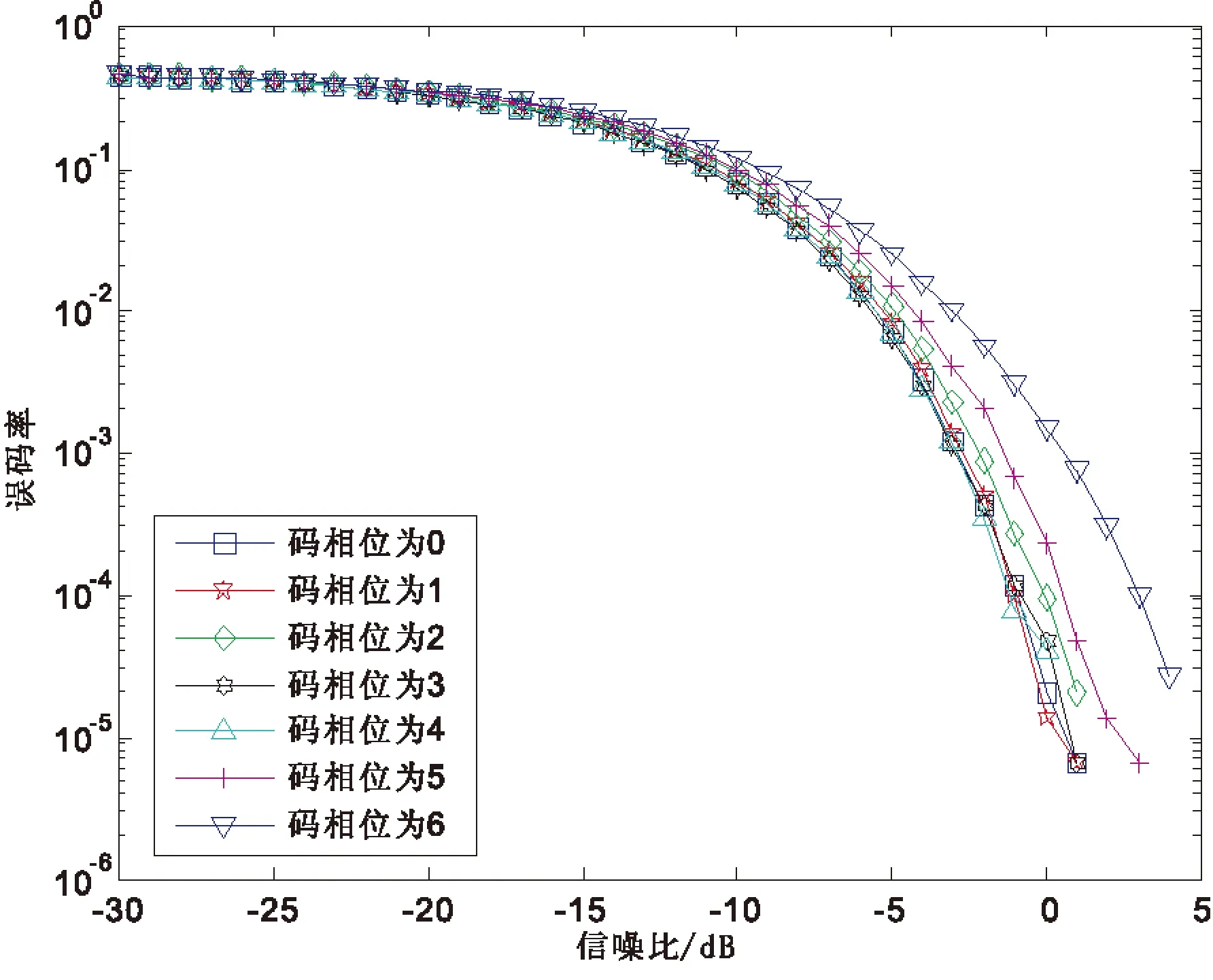
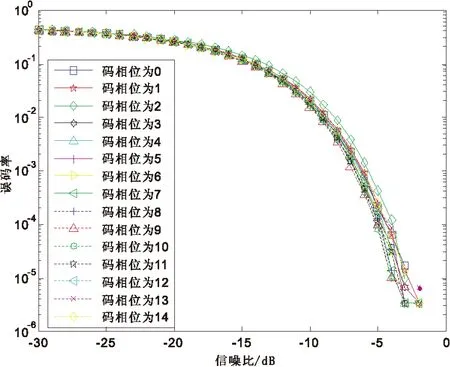
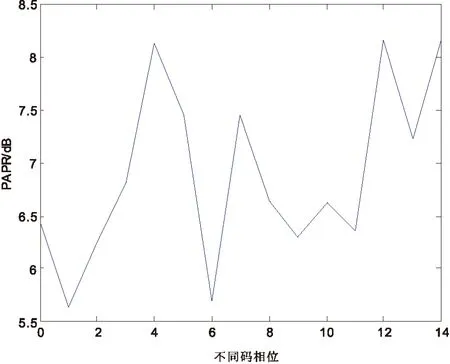
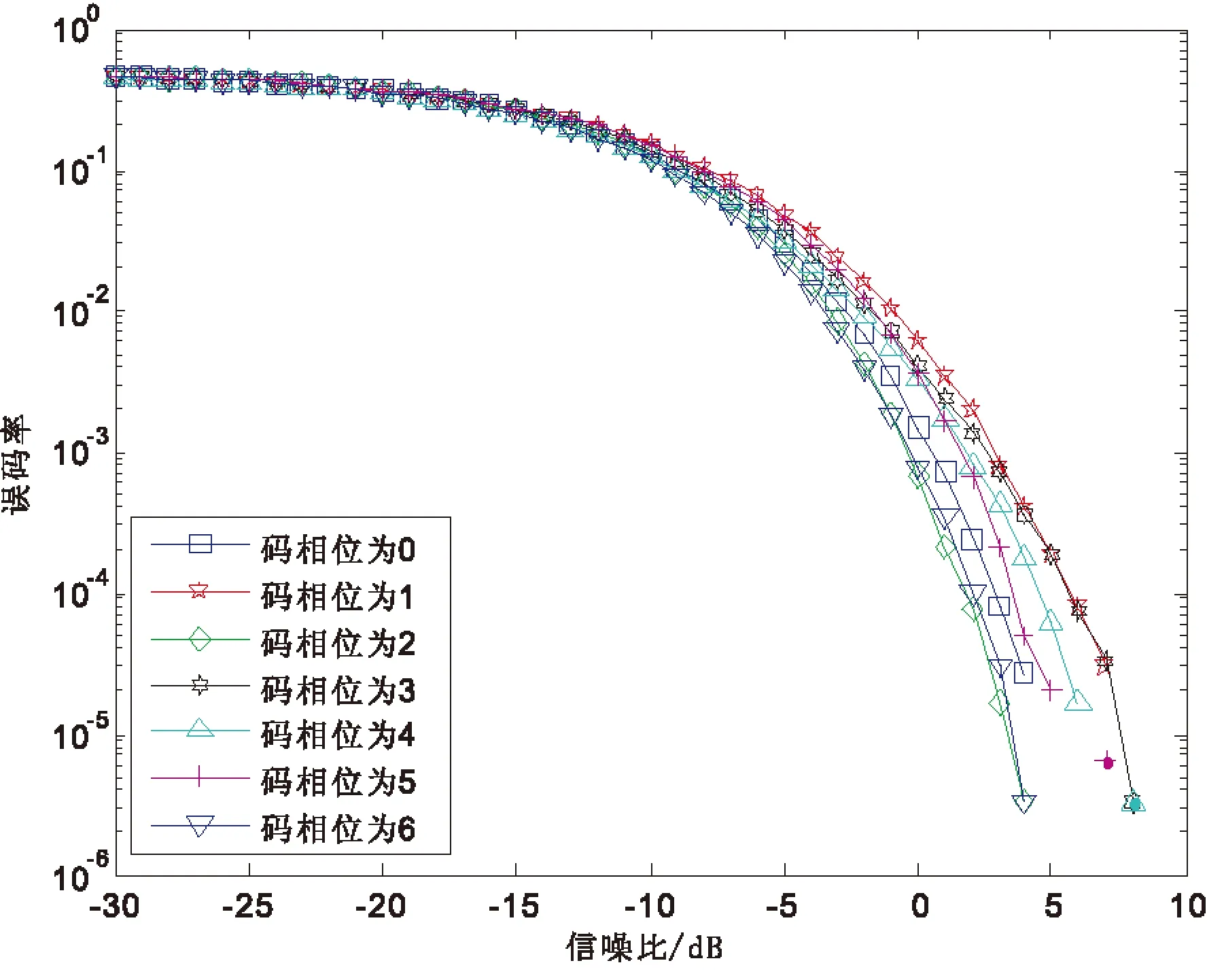
K代表多径信号和主径信号交叠的码片数,K 发射信号可以表示为 (7) 其中,b为信息,Ai为发射信号的幅度,ci(t)为扩频序列,其中i为信号携带的载波数目,其中1≤i≤M,φi为每个频点载波的相位. 同样,经历水声信道,接收信号也可以表示为 (8) 其中,Ak,i为接收信号的幅度,τ为时延,k表示路径,0≤k≤L,L为可分辨多径的最大数目.在最小相位系统中,k为0时表示的是主径,n为噪声. 在完成同步之后,每符号积分输出可以表示为 (9) 其中,Ai为每一载波的主径幅度.L-1为对此符号产生影响的多径数目.等式右端第一项为期望的信号,第二项为多径带来的干扰,第三项为噪声项. 在频域扩频水声通信系统中,存在着双重的判断标准,就是误码率(BER)和峰均功率比(PAPR),其中,PAPR定义为 (10) 其中,xn表示待观察的信号. 在衰落信道下,序列的周期自相关特性(PACF)和非周期自相关特性(AACF)都对直接序列扩频(DSSS)有一定的影响.以码长为7的m序列为例,其不同码相位的PACF都是一个二值函数,但是其不同码相位的AACF有所不同,如下图1、2、3所示: 图1 AACF旁瓣(码长为7) 图2 AACF的旁瓣方差(码长为7) 图3 不同码相位的AACF旁瓣最大值(码长为7) 从图1到图3可以看出,虽然不同码元相位的m序列拥有着相同的PACF,但是其AACF特性却有着很大的不同,码相位为0表示无循环移位.本文主要通过AACF的旁瓣方差和最大值来描述AACF特性,可以看出其方差相差5倍,而其旁瓣最大值最多相差两倍.从图中也可以看出,AACF的旁瓣的方差和其最大值成正相关. 以下图4、5、6是码长为15的m序列AACF特性曲线: 图4 AACF旁瓣(码长为15) 图5 AACF的旁瓣方差(码长为15) 图6 不同码相位的AACF旁瓣最大值(码长为15) 可以看出,对于码长为15的m序列,其AACF旁瓣方差的最大值是最小值的3倍左右.其旁瓣最大值的峰值和谷值之间相差2倍以内.PACF和PPCF同时决定着DSSS水声通信系统的性能.而水声信道CIR的时延扩展,多径强度和时变速率都是这两种特性影响系统性能的因素.以下就以实测海洋信道为例,来研究不同码相位对系统的影响.图7是仿真使用的信道冲激响应图. 仿真中使用的中心频率为48 kHz,带宽为6 kHz-10 kHz.采用m序列,码长为7.可得其切普速率为2 000 chip/s,通信速率为285.7 bps,每符号只载有1 bit信息.以下是根据此信道冲激响应图仿真得到的不同码相位的误码率(BER),如图8、9所示. 图7 仿真使用的CIR 图8 时域扩频不同码相位的BER(码长7) 从图8可以看出,其不同码相位在衰落信道下的抗噪声能力相差很大,以10-3BER为例,其抗噪声能力最大相差4 dB左右.这说明选择不同的码相位对系统性能有着至关重要的影响.本图中码相位为0时系统获得了最好的性能.本曲线与AACF的方差和最大值存在一定的相关性,但又不是完全按照AACF的特性排布.这是因为水声信道是稀疏的,AACF的影响存在着一定的随机性. 从下图9中可以看出,在不同码相位的条件下,在衰落信道下的抗噪声能力在10-3BER的情况下相差1 dB以上.而且码相位为0时的情况并不是最好的情况.这也说明码相位优选对于系统性能的提高是有意义的. 以上讨论了码相位对时域扩频的影响,下面来讨论其对频域扩频的影响.下图10、11是不同码相位的PAPR,仿真参数中带宽、中心频率和采样率不变. 图9 时域扩频不同码相位的BER(码长15) 图10 不同码相位的PAPR(码长为7) 从图中可以看出,基于码长为7的系统在不同的码相位下PAPR最大值和最小值相差两倍以上,而基于码长尾15的水声通信系统在不同的码相位下PAPR相差2 dB以上.而且,图10和图11中的PAPR展现出与AACF旁瓣方差变化的规律有着一定的相似性. 图12是频域扩频水声通信系统在不同码相位下的BER表现,仿真使用的是码长为7的m序列. 从图12可以看出,不同码相位的通信系统在衰落信道下的抗噪声能力有着一定的差异,以10-3BER为例,其不同码相位需要的信噪比相差3 dB以上.而且其码相位为0时并不是具有最好抗噪声能力的情况,这也就显示出了码相位优选的重要意义所在.码相位的选择可以在系统抗噪声能力和PAPR之间做出一个权衡.综上,仿真研究了基于不同码相位的时域扩频和频域扩频水声通信系统.可以看出,基于优化码相位的时域和频域扩频水声通信系统可以表现出更优良的性能. 图11 不同码相位的PAPR(码长为15) 图12 频域扩频不同码相位的BER 本文研究了基于不同码相位的时域和频域扩频水声通信系统,研究了不同码相位下序列的AACF特性,系统的PAPR特性和BER特性.可以得到这样的结论:优选码相位的时域和频域扩频水声通信系统有着更好的性能,根据系统的需要,可以对频域扩频水声通信系统的PAPR和BER进行优化.本文提出的方案在不增加系统复杂性和实时性的情况下,提高了系统的性能,可以为中远程水声通信,低功耗水声通信,低探测可能性水声通信和水声通信网提供一种新的备选方案. [1] Kilfoyle D B, Baggerroer A B. The State of art in underwater acoustic telemetry[J]. IEEE J.Ocean Eng, 2000, 25(1): 25. [2] Stojanovic M, Preisig J. Underwater acoustic communication channels:propagation models and statistical characterization[J]. IEEE Commun.Mag, 2009, 47(1): 84-89. [3] Stojanovic M, Proakis J P, Rice J A. Spread spectrum underwater acoustic telemetry[C]. IEEE OCEANS Conf.Nice:France, 1998(2): 650-654. [4] Ling J, He H, Li J. Covert underwater acoustic communications[J]. J.Acoust.Soc.Am, 2010, 128(5): 2 898-2 909. [5] Sozer E M, Stojanovic M, Proakis J G. Underwater acoustic networks[J]. IEEE J.Ocean Eng, 2000, 25(1): 72-83. [6] Proakis J G, Sozer E M, Rice J A. Shallow water acoustic networks[J]. IEEE J.Ocean Eng, 2001, 39(11): 114-119. [7] Freitag L, Stojanovic M, Singh S. Analysis of channel effect on direct-sequence and frequency-hopped spread spectrum acoustic communication[J]. IEEE J.Ocean Eng, 2001, 26(4): 586-593. [8] 于 洋,周 锋,乔 钢.M元码元移位键控扩频水声通信[J].物理学报,2012,61(23):1-7. [9] 何成兵,黄建国,韩 晶,等.循环移位扩频水声通信[J].物理学报,2009,58(12):8 379-8 385. [10] 殷敬伟,惠俊英,王逸林,等.M元混沌扩频多通道Pattern时延差编码水声通信[J].物理学报,2007,56(10):5 915-5 920.1.2 频域扩频水声通信系统

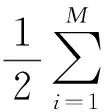
2 仿真分析
2.1 不同码相位对时域扩频的影响


2.2 不同码相位对频域扩频的影响

3 结语

