相位信息遥感图像边缘检测方法的实例检测分析

张雪侠

(陕西国际商贸学院，陕西 西安 712046)

1 概 述

基于高分辨率的空间遥感图像的边缘主要用来描述地面物体(如：道路、建筑物、河流等)的结构信息，在实际的业务处理过程中，边缘检测对于利用遥感信息解决图像分割、土地覆盖等领域的研究具有重要的意义。国内外许多学者都致力于遥感图像应用的研究，如武汉大学测绘学院、中国矿大的地理信息研究团队等，学者们针对不同的应用场景提出了大量的边缘检测算法，大多数均是基于梯度的算法[1-3]。

国外对于边缘检测的研究一直处于领先的位置，如Roberts等最先研究了基于梯度的特征提取检测算法，但在实践过程中，利用该类算法对物体进行检测存在图像噪声干扰等问题；为此，Marr等引入更多的系统算法从遥感图像中检测更为重要的边缘信息；而由于不同物体的边缘存在不同的特征类型，因此Morrone等发现了相位一致性理论，主要用于局部能量模型的图像边缘检测中；Kovesi利用Log Gabor滤波器来计算局部能量，使得Morrone等人研究的相位一致性模型在边缘检测过程中更为方便。Log Gabor滤波器经常用于图像处理，用于检测纹理和边缘特征、指纹图像增强、编织缺陷检测及人眼虹膜识别等。本文主要采用Log Gabor滤波器在频域中提取边缘特征，同时本文以2017.11.22采集的武汉地区部分景观遥感影像，像素为512×512，包含红色，绿色，蓝色、近红外波段的多光谱数据，空间分辨率2.44 m，全色空间分辨率0.61 m，具体影像参数见表1。

表1 遥感影像参数

为了获取更好的遥感图像上更多的影像细节，对图像对象按照全色波段进行边缘识别，如图1所示为全波段遥感影像图，通过边缘识别主要识别图中河流、建筑等物体的边界。

2 检测分析方法介绍

2.1 傅里叶变换

傅里叶变换已经广泛应用于许多领域的研究，如数字信号处理(DSP)和图像处理等领域，在图像处理研究中，由于图像的离散性，因此通过二维离散傅里叶变换(DFT)定义，如下式[2-6]。

图1 全波段原始遥感图像

(1)

由于DFT的变换速度较低，因此相关学者提出了FFT来提高变换的速度，其中幅度谱表示图像的能量分布、相位谱表示图像特征的位置以及图像的结构细节。对图像进行傅里叶变换后，可以得到幅度和相位谱，如下式所示。

(2)

(3)

其中|F(u,v)|和φ(u,v)分别表示幅度和相位谱，I(u,v)和R(u,v)分别表示图像的实部和虚部。本文利用遥感图像的幅度谱进行边缘检测，在边缘检测处理之前，幅度谱定义如下规则。

1)幅度谱的DC(直流)分量表示图像的平均值；

2)距离直流分量距离越远，幅度越大；

3)能量谱主要集中在直流分量上；

4)边缘的方向与边缘频率能量的方向正交。

由于低频和高频之间的能量差异显着，幅度谱由对数函数转换。因此，幅度谱可以通过以下定义来获得。

D(u,v)=log[1+|F(u,v)|]

(4)

当原始的遥感图像的行数或列数彼此相同时，能量分布的取向与空间域中的边缘特征或纹理的延伸方向正交。另外，频率能量的分布对于直流分量是对称的。大部分能量集中在频谱图像的中心。根据公式2和公式4对图1进行处理，所得的幅度谱如图2所示，与图1进行对应，图2中较为明显的线条分别于图1中的边缘进行对应，如图中A和B表示原图像的两行特征。其中A线较为清晰、连续；而B线呈现一定的周期性亮点显示，这是由于原来的全色带的农田有很多周期性的纹理特征。

图2 对图1进行频率谱处理后的结果图

2.2 边缘特征的频谱分析

本文采用半径采样和角度采样对遥感图像进行分析处理，如图3为半径采样的样例图，图4为角度采样的样例图。对于具有不同频谱能量的遥感图像均可以通过半径采样和角度采样联合获取能量分布曲线，为Log Gabor滤波器提供样本[7]。

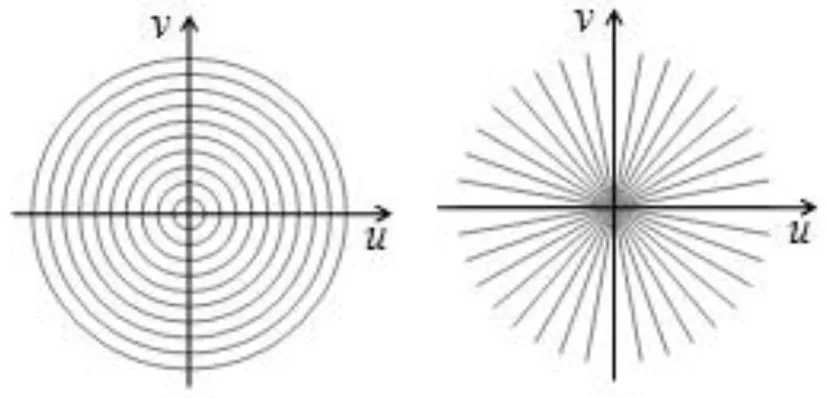
图3 半径采样样例 图4 角度采样样例

如图5所示为采用角度采样进行分析的结果图，结果显示，当角度采样在0(°)～180(°)的角度之间有3个峰值，分别出现在2(°)、83(°)、176(°)，因此根据经验分析可获取边缘特征的更多细节[8]。

如图6所示为采用半径采样进行分析的结果图，结果显示，整个采样结果随着频率变高而急速下降，而在频率为18处有一个有一个较小的峰值，表明该采样结果包含了更多的原始遥感图像信息。

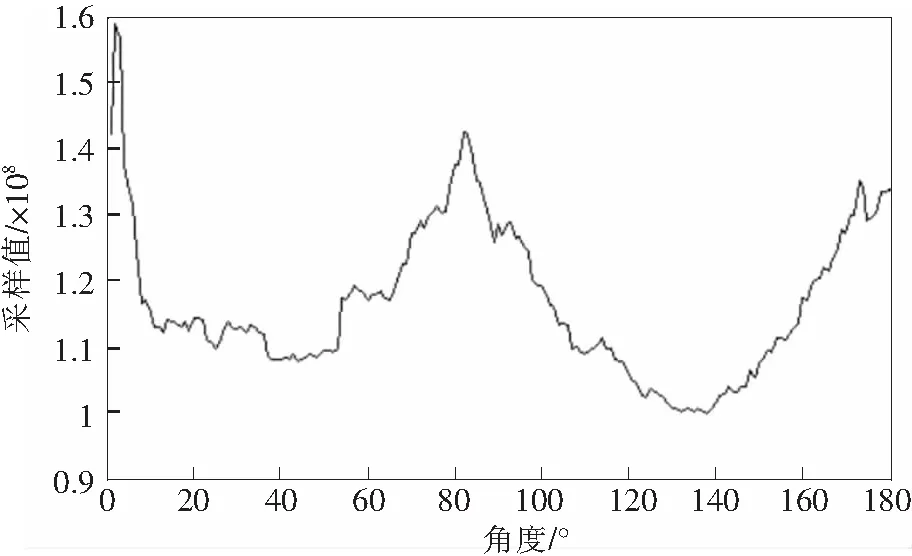
图5 角度采样结果

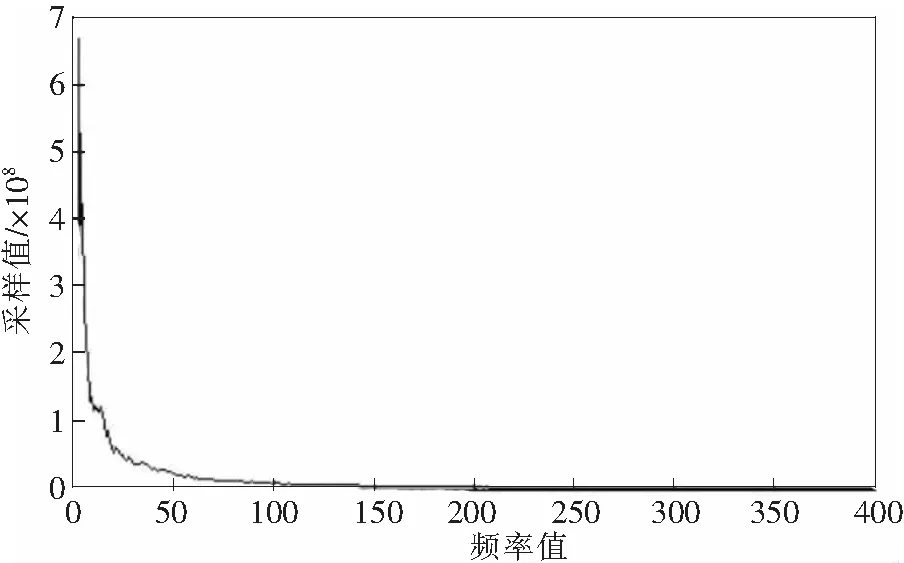
图6 半径采样结果

2.3 采用Log Gabor滤波器实现边缘检测

根据一维Gabor函数扩展定义两维Gabor函数[9]，如下公式所示。

j(u0x+v0x)}

(5)

如公式(5)中的σx和σy分别决定Gabor滤波器在X和Y方向上的长度，(u0,v0)用来定义滤波器的中心频率，那么在频域中对Gabor函数进行定义如下。

(6)

定义f为滤波器的中心频率，θ为正弦平面波的方向，γ和η分别是高斯包络线沿主，次方向的标准偏差；那么定义如下。

u′=ucosθ-vsinθ

v′=usinθ-vcosθ

其中γ、η和θ决定了频域中Gabor滤波器的形状，而G(u,v)是一个高斯函数。然而，构造具有任意宽带宽和零DC分量的Gabor函数。因此，为了更有效的应用，提出了Log Gabor滤波器。在Log Gabor滤波器中没有影响边缘检测输出的DC分量，此外，它在高频端具有延长的尾部，使得它可以比普通的Gabor滤波器更有效地编码自然图像。Log Gabor函数的定义如下。

(7)

遥感图像的边缘检测过程可以表示如下。

1)对图像f(i,j)进行傅里叶变换，得到频域F(u,v)；

2)通过Log Gabor滤波器对频谱分析进行设计；

3)用Log Gabor滤波器产生点积F(u,v)；

4)逆傅立叶变换2)的结果;

5)获取3)的结果的实际分量。

3 分析结果

根据频谱分析，主频率能量主要分布在2(°)、83(°)和176(°)的角度附近。由于2(°)和173(°)接近，因此根据测试结果设计了两个Log Gabor滤波器，角度分量的中心频率分别设置为177.5(°)和82(°)，从原始图像中提取边缘特征，此外，Log Gabor滤波器的径向分量的中心频率被设置为200，以便检索更多的高频信息。如图7所示为两个Log Gabor滤波器组识别的边缘结果图。

图7 边缘结果图

最后，通过Log Gabor滤波器组与原始图像之间的点积对遥感图像进行边缘检索，如图8所示为采用本文所提出的检测算法对图1中的遥感图像进行边缘检测，图中可见农田里的山脊、车间的边界、水体与土地之间的边界等边缘都很容易被检测到。

图8 原始遥感图边缘检测结果图

4 结 论

综上所述，本文提出了一种新的高分辨率遥感图像边缘检测算法。首先对图像进行离散傅立叶变换，得到幅度谱；其次，通过半径和角度采样来分析幅度谱来定位边缘分布；通过所设计的对数Gabor滤波器的滤波器组，与频谱原始的高空间分辨率遥感图像相乘利用逆傅里叶变换对结果进行变换来检索边缘检测。通过最终的实验结果证明本文所提出的边缘检测算法有较好的检测性能。

[1] 王晨阳,叶梦轩,李梓豪.基于相位一致的遥感图像边缘检测方法[J].中国锰业,2017,35(2):175-177.

[2] 陈洋,范荣双,王竞雪,等.结合相位一致和分水岭变换的高分辨率遥感影像分割方法[J].激光与光电子学进展,2017,54(9):381-386.

[3] 徐全飞,冯旗.基于SURF和矩阵乘法的超大规模遥感图像亚像素配准算法研究[J].红外技术,2017,39(1):44-52.

[4] 陈竹安,胡志峰,杨希鹏.基于改进的soble算子和zernike矩遥感图像边缘检测[J].湖北民族学院学报(自然科学版),2017,35(2):229-234.

[5] 王小伟. 基于小波变换与Log Gabor滤波的虹膜识别系统的设计与实现[D].济南：山东大学,2017.

[6] 魏月纳,吴锡生.基于Gabor融合和分块处理的人脸识别算法[J].计算机工程与设计,2017,38(3):719-723.

[7] 李雅倩,张少伟,李海滨,等.一种基于Gabor小波及互协方差降维运算的人脸识别方法[J].电子与信息学报,2017,39(8):2023-2027.

[8] 戴激光,张力,朱恩泽,等.遥感影像主特征线检测[J].遥感学报,2017,21(2):228-238.

[9] 杨瑞,张云伟,苟爽,等.Gabor特征与深度信念网络结合的人脸识别方法[J].传感器与微系统,2017,36(5):68-70.