基于机电耦合的反射面天线副面位置调整方法

项斌斌, 王从思, 王 伟, 连培园, 张树新, 保 宏

(1. 西安电子科技大学电子装备结构设计教育部重点实验室, 陕西 西安 710071;2. 中国科学院新疆天文台, 新疆 乌鲁木齐 830011)

0 引 言

随着无线电与电子技术的不断发展,反射面天线广泛应用于微波通讯、军事侦察和射电天文等领域。近年来射电天文研究不断深入,反射面天线作为重要的天文观测工具已朝着高频段、高增益和大接收面积的方向发展[1],我国已在贵州建设了世界最大口径的500 m球面射电望远镜(five hundred meters aperture spherical radio telescope, FAST),同时在新疆正在建立世界最大口径的110 m全可动射电望远镜(QiTai radio telescope, QTT)[2],它们都将主要用于天文观测。

反射面天线是一种典型的机电集成的电子装备,在重力、温度、风荷等载荷影响下,其结构容易产生变形进而影响电性能,导致波束变形、增益下降、副瓣升高[3]。针对天线结构变形对电性能的影响研究,长期以来一直是结构设计和微波技术研究的热点。为了减小天线结构变形的影响,天线设计者提出了保型设计、主动面调整、副面(也称副反射面)调整等方法来补偿结构变形对电性能的影响[4-7]。近年来以主动面调整、副面调整、主动副面等为代表的主动补偿方法得到了广泛关注和研究,其补偿效果受到天线工程技术人员的期待。

文献[8]针对反射面天线最佳相位中心,以电性能为目标对主焦点馈源位置进行优化,寻求变形反射面的最优相位中心。文献[9]针对反射面天线馈源的位置和姿态的调整,基于口径场法通过远场与口径场误差的关系反推馈源的位置和姿态的调整量。上述文献主要针对天线主面变形而对馈源的位姿进行修正,然而对于双反射面天线而言,馈源一般位于靠近主面顶点的副焦点处,其结构尺寸和质量较大,不宜进行频繁调整,通常采用对副面位置进行调整以提高天线的口径效率。文献[10-11]针对赋形卡氏天线主面变形导致电性能变差的情况,对变形主反射面进行分段吻合,采用最佳几何匹配的思想以找到新的副面位置来补偿主面变形。该方法主要从几何的角度考虑,对天线变形后的表面形状进行拟合,将副面调整到理想的几何位置,其前提是需要对天线反射面面形进行精确获取和描述,这对于表面测量和结构分析的精度要求较高;然而从机电耦合角度考虑,对于一部天线而言,可直接通过调整副面位置并对天线所收发信号质量的分析来直接衡量副面位置的优劣。因此为了更加快速便捷地确定副面的最佳位置,可通过射电望远镜天线的接收机和终端直接获得天线的电性能,基于机电耦合思想对副面位置进行实时调整,从而达到补偿天线结构变形提高口径效率的目的。

针对大型反射面天线副面位置调整方法,本文基于机电耦合思想,从天线远场方向图与口径场相位误差之间的关系出发,研究了副面位置与电性能之间的关系,推导了副面位置调整参数与天线远场方向图间的关系式。采用最优化的方法建立了确定副面最佳位置参数的优化模型,以增益最大为目标通过优化的方法获得副面的最佳调整量。以26 m双反射面天线为例进行仿真试验,验证了文中所提方法的有效性。该方法是直接以电性能目标的副面调整主动补偿方法,比基于反射面结构变形拟合的副面调整更直接和有效,且更能准确的反映天线的性能。

1 反射面天线机电耦合模型

反射面天线远场的辐射方向图可采用面电流法或口径场法获得。本文主要采用口径场法在天线口径面上进行积分获得天线的远区辐射场。口径场法先根据几何光学原理由馈源辐射场求出反射面的口径场分布,由口径场相位分布与远场的傅里叶变换关系,反射面天线几何关系示意图如图1所示,远场方向图[12]可表示为

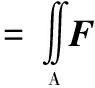
exp(jΔφ)r′dr′dφ′

(1)

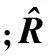
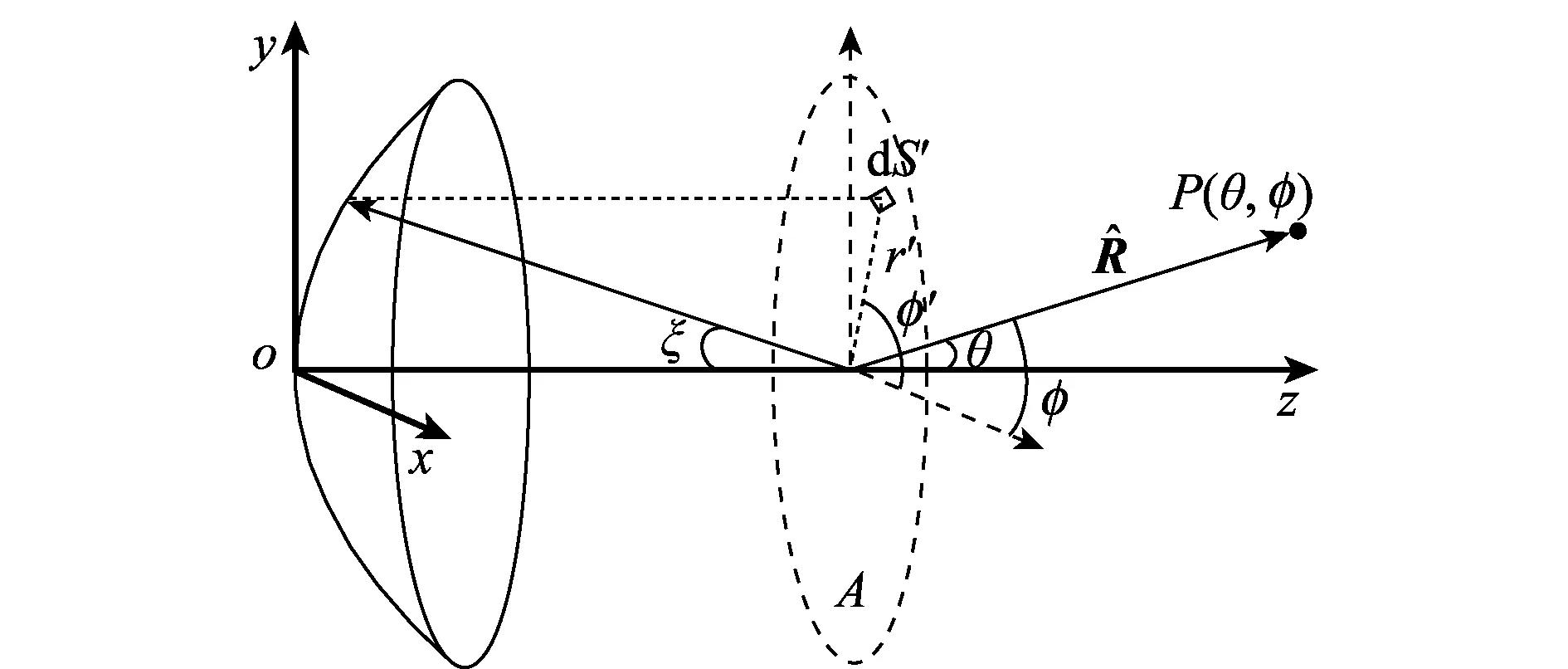
图1 反射面天线几何关系示意图Fig.1 Schematic diagram of the reflector antenna

本文主要针对大口径反射面天线主面变形和副面位置偏移误差进行副面调整补偿,由于重力载荷等产生的主面变形和副面偏移误差通常不大,与天线口径和焦距相比属于小变形误差,故当天线位移误差较小时,可忽略其对口径面电磁场幅值的影响,只对口径面相位产生影响,即位移误差只引起口径面相位误差[12]。

2 由结构变形引起的天线口径场相位误差

由于受重力、温度和风荷等载荷影响,天线结构将产生变形,主要表现为背架结构变形、副面支撑结构变形和馈源支撑结构变形(主焦馈电形式),它们将导致天线反射面的表面误差、副面位置误差和馈源位置误差。此外,由于天线的加工和装配存在一定误差,也将引起天线表面的制造误差和装配误差。根据天线误差理论[3,13],这些误差会对天线电性能产生影响,引起口径面上光程差,使口面上的辐射场产生相位误差,进而导致远场电性能变差。这里主要考虑由天线结构变形引起的反射面表面误差和副面位置误差对口径场相位误差的影响。根据几何光学原理,反射面表面误差和副面位置误差在口径场引起的总光程差由各自引起的光程差的叠加,即

δ0(r′,φ′)=δp(r′,φ′)+δs(r′,φ′)

(2)

式中,δ0为总光程差;δp为反射面表面误差引起的光程差;δs为副面位置误差引起的光程差。

由于口径面各点光程差的差异进而导致口径面上辐射场各点相位产生差异,即引起口径场相位误差。相位误差与光程差的关系式为

Δφ(r′,φ′)=k·δ(r′,φ′)

(3)

2.1 反射面表面误差引起的口径场光程差

图2为卡塞格伦双反射面天线几何示意图,图中a和c表示副面半短轴和半焦距,θp表示对入射光线经主面反射后与入射光线的夹角,θf表示经副面反射后的光线与主光轴的夹角。

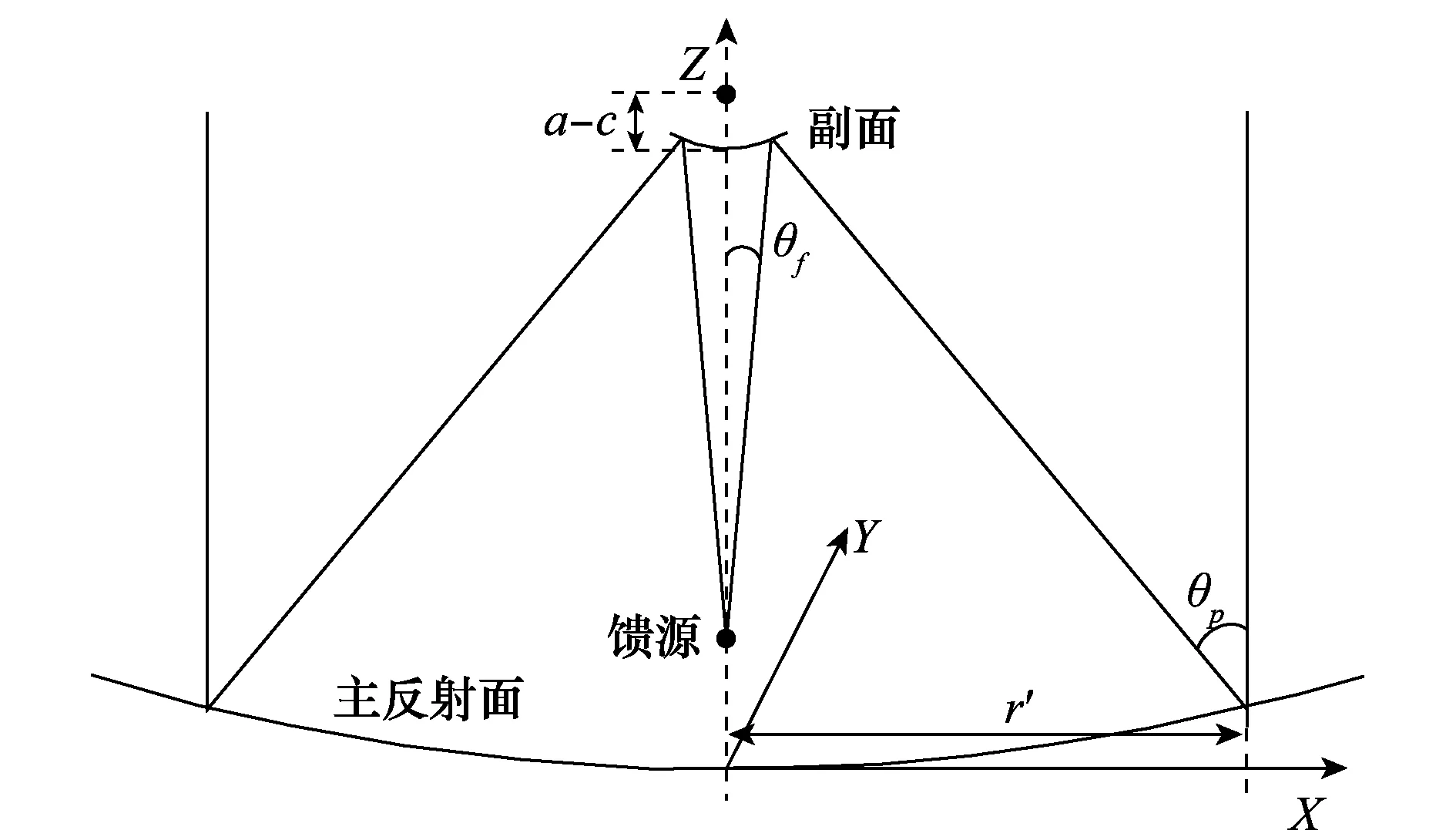
图2 卡塞格伦双反射面天线几何示意图Fig.2 Geometry diagram of the Cassegrain dual reflector antenna

假设反射面上点(r′,φ′)的表面误差为Up=[Δxp,Δyp,Δzp]T,则由表面误差引起的口径面光程差可以表示[13-14]为

δp=2·(Δxpcosα+Δypcosβ+Δzpcosγ)·cosγ

(4)

写成矩阵形式为

δp=[2cosαcosγ,2cosβcosγ,2cos2γ]·

[Δxp,Δyp,Δzp]T=Cp·Up

(5)

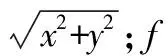
2.2 副面位置姿态误差引起的口径面光程差

假设副面支撑结构变形导致副面产生刚体位移误差Us=[Δxs,Δys,Δzs]T和转角误差φs=[Δφx,Δφy]T,则由卡塞格伦天线副面位置误差引起的口径面光程差[14-15]为

δs=(-Δxscosφ′-Δyssinφ′)·(sinθp-sinθf)+

Δzs(cosθp+cosθf)+(c-a)·

(Δφxsinφ′-Δφycosφ′)·(sinθp+M·sinθf)

(6)

写成矩阵形式为

δs=[-cosφ′·(sinθp-sinθf),-sinφ′·(sinθp-sinθf),

cosθp+cosθf,(c-a)·sinφ′·(sinθp+M·sinθf),

(c-a)·cosφ′·(sinθp+M·sinθf)]·

[Δxs,Δys,Δzs,Δφx,Δφy]T=Cs·Q

(7)

式中

Q=[Δxs,Δys,Δzs,Δφx,Δφy]T

对于格里高利形式天线副面位置误差引起的口径面光程差关系式只需将式(6)中的(sinθp-sinθf)换为(sinθp+sinθf)即可。

由反射面表面误差和副面位置误差引起的口径面总光程差即为式(2)所表示的形式,口径场相位误差则为式(3)所表示的形式。综合不同的变形误差,则口径面的相位误差可表示为

Δφ=k·C·U

(8)

式中,U表示不同结构变形矩阵;C表示系数矩阵;k表示自由空间波常数。

3 副面位置偏移影响

双反射面天线副面移动将引起位置偏差,该偏差可分为横向偏差和纵向偏差,其中横向偏差表示副面沿垂直于主反射面对称轴方向的偏移,纵向偏差表示副面沿主反射面机械轴方向的偏移,即沿焦距方向偏差。在式(6)中Δxs、Δys表示副面横向偏移量,Δzs表示纵向偏移量。副面的横向偏移和纵向偏移对天线的指向、效率和方向图的影响效果有所差别,接下来对副面位置偏移的影响进行分析。这里主要分析副面沿x、y、z方向平移偏差的影响,副面的转动偏移Δφx、Δφy的影响效果可等效为主反射面和馈源的刚体平移和旋转偏差影响[14],其影响可通过副面平移进行等效补偿,这里不再进行分析。

3.1 副面位置调整对口径面相位影响

根据式(6),副面沿x、y、z方向的移动引起的口径面相位误差分布如图3所示,其中,图3(a)和图3(b)为副面沿x、y方向移动引起的的相位误差分布,即横向移动;图3(c)为副面沿z方向移动引起的相位误差分布,其纵向移动。从图中可以看到副面横向移动导致口面相位误差分布呈现不对称分布,按照图2所示的坐标系,副面沿x方向移动,相位分布呈现水平不对称,且呈现水平连续单调变化趋势;同理副面沿y方向移动,相位分布呈现垂直不对称。然而,副面沿纵向移动引起的相位误差分布则呈现旋转对称形状,且由中心向外逐渐单调变化。

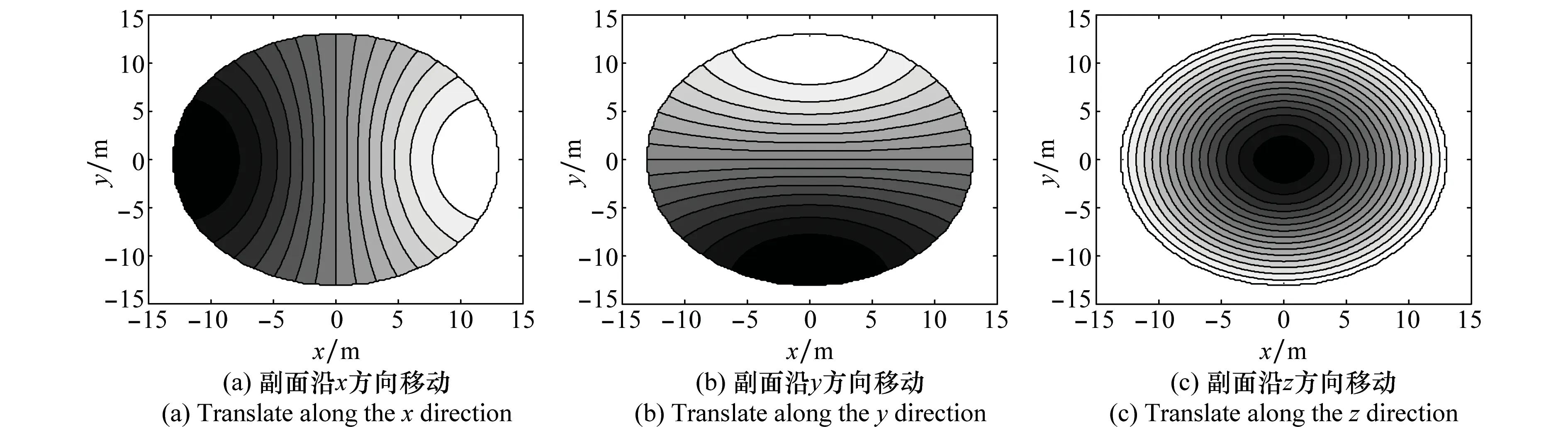
图3 副面沿xyz方向移动引起的口径面光程差分布Fig.3 Path length difference in aperture plane result from subreflector translate along with x, y, z direction

根据几何光学射线传播反射理论,副面横向、纵向移动后的光线传播示意如图4所示,虚线为副面移动后光线。从图4(a)可看出,副面移动前馈源F发出球面光线,经副面S一次反射和主面M二次反射后变为与天线机械轴平行的平行光线进行传播,其等相位面为与天线口面平行平面EPP,此时天线主光轴为OA,其与主面机械轴重合;当副面横向移动Δx后,馈源F发出球面光线,经副面S′一次反射和主面M二次反射后变为与天线机械轴有夹角的平行光线进行传播,其等相位面为与天线口径近似平行的平面EPS′,此时天线主光轴为OA′,其与主面机械轴存在夹角Δθ,则天线产生指向偏差,且偏差方向与副面移动方向相反。图4(b)为副面纵向移动光线传播图,副面纵向移动Δz后,馈源F发出球面光线,经副面S′一次反射和主面M二次反射后变为与天线机械轴平行的平行光线进行传播,其等相位面为一个旋转曲面EPS′,其旋转轴(即主光轴OA′)与天线主面机械轴重合,则天线无指向偏差。

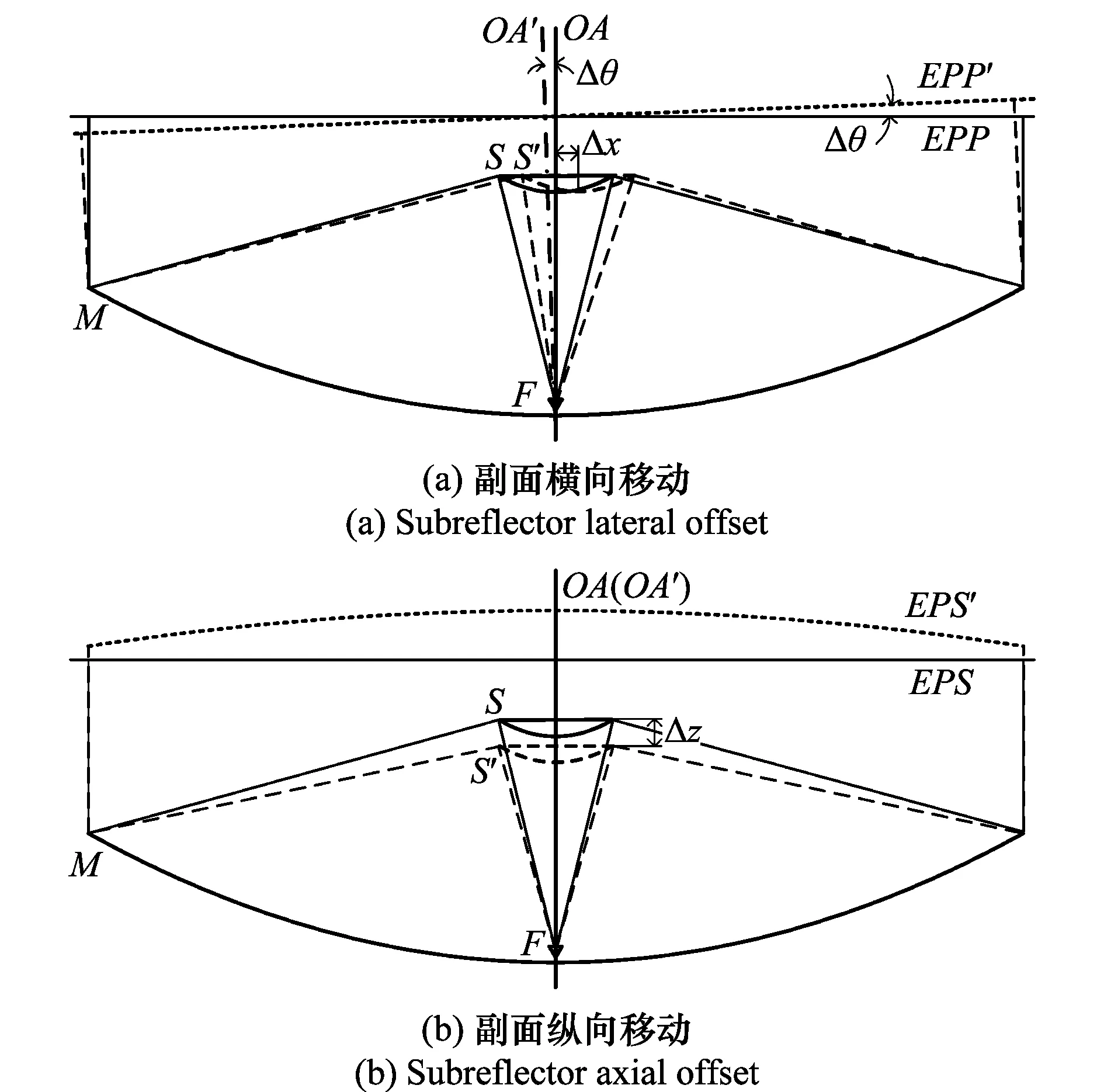
图4 副面移动光线反射传播示意图Fig.4 Diagram of light propagate after subreflector offset

3.2 副面位置调整对远场影响

副面横向、纵向移动移动导致的方向图变化如图5所示,虚线为副面移动后方向图,从图5 (a)中可看出,副面横向(沿x正方向)移动将导致方向图主瓣发生偏移(向x负方向),主瓣最大值下降,副瓣较未移动前有所抬高,且出现左右不对称(主瓣左侧电平低,右侧电平高),较高副瓣电平方向与副面横向移动方向一致。从图5(b)中可看出,副面纵向移动将导致方向图,主瓣最大值下降副瓣抬高,但主副瓣未发生偏移,仍左右对称。由图4(a)和图4(b)可知,副面横向偏差和纵向偏差都会导致增益降低,横向偏差导致的天线指向偏差影响更大,而纵向偏差导致的方向图下降幅度更大,同时副瓣抬升幅度更大,这表现出副面纵向移动偏差对天线增益影响更加敏感。

由之前副面偏差对口径面相位和远场影响分析可知,副面横向偏差将引起口径面相位误差呈现出沿偏差方向的单调变化的分布特征,这将导致远场增益下降;左右副瓣不对称,较高副瓣方向与副面横向移动方向一致;指向产生偏差,且偏差方向与横向移动方向相反。副面纵向偏差将导致口径面相位误差呈现由中心向外单调变化且旋转对称的分布特征,这将导致远场增益明显下降,副瓣升高。副面横向、纵向偏差都会导致天线增益下降,只有使副面横向和纵向偏差都降低,才会使天线增益升高,同时指向误差减小,提高天线性能。通过远场方向图的副瓣形状和指向偏差方向来粗略判断出副面位置的横向偏移方向,并可据此将副面向相反方向进行调整,以减小副面横向偏差,补偿电性能。

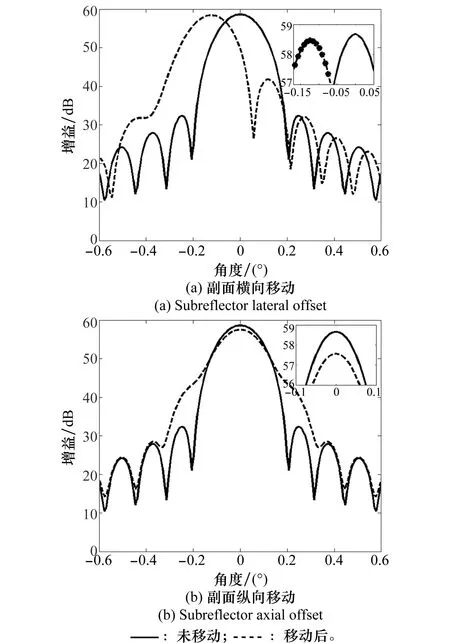
图5 副面移动后天线远场方向图Fig.5 Antenna far field gain pattern after subreflector offset

4 副面位置调整与远场的关系

当天线主反射面朝向某一仰角时,其结构将出现一定变形,即主反射面表面变形误差和副面位置误差,它们将引起口径面的光程差和相位误差,进而影响远场的辐射特性,使增益和效率下降。根据机电耦合模型,结构变形与远场的关系式(1),考虑到Δφ为小位移引起的小相位误差,可将ejΔφ进行一阶泰勒级数展开,则式(1)可表示为

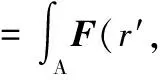
(9)

式中,第一项E0(θ,φ)为口径场无相位误差时的远区辐射电场;第二项表示口径场相位误差引起的辐射电场偏差。

当副面位置调整后,即Q′=Q+dQ,则口径场相位误差为

Δφp+Δφs+dΔφs=Δφ+dΔφs

(10)

dΔφs=k·Cs·dQ

(11)

式中,dQ表示副面位置调整量,即dQ=[dΔxs,dΔys,dΔzs,dΔφx,dΔφy]T。

副面调整后远场方向图关系式为

E′(θ,φ)=E1(θ,φ)+

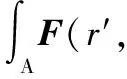
(12)

将式(11)代入式(12),则

E′(θ,φ)=E1(θ,φ)+

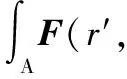
(13)

令

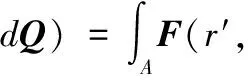
(k·Cs)dS′·dQ=H·dQ;

则式(13)用矩阵形式可表示为

E′(θ,φ)=E1(θ,φ)+f(θ,φ,dQ)

(14a)

E′(θ,φ)=E1(θ,φ)+H·dQ

(14b)

式(14)即为双反射面天线副面位置调整后远场方向图与位置调整量的关系式,可称为副面调整影响模型,其中矩阵H为与(θ,φ)有关的调整系数矩阵,可根据口径面上的点的分布(r′,φ′)、馈源初级方向图和观察点位置(θ,φ)提前获得;E1(θ,φ)可根据提前测得的反射面表面误差和副面位置误差通过计算获得。

通过式(4)～式(7)即建立了反射面表面误差和副面位置误差与口径场相位误差间的关系式,式(9)和式(14)也建立了远场和副面位置调整量间的关系式,使得以远场最优为目标而直接对副面调整量dQ进行优化可以实现。

5 以电性能最优为目标的副面位置实时调整方法

5.1 副面位置调整量优化模型

为了使天线主反射面朝向某一仰角时结构变形影响最小,通过对副面位置进行调整以获得天线在该仰角的最优电性能。这里考虑采用对副面位置调整量dQ进行优化的方法,以相对增益最大为目标,获得副面最佳位置调整量,则副面最佳调整问题即转化为电性能最优化问题,优化目标为相对增益,优化变量为副面位置调整量向量dQ,具体优化问题数学模型为

Find: dQ=[dΔxs,dΔys,dΔzs,dΔφx,dΔφy]T,

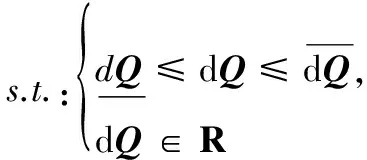
(15)

该优化模型的物理意义表示在副面调整的可行域中寻找一组副面调整量参数dQ,使调整后的天线增益与调整前的增益比值最大,即相对增益最大。故通过采用合适的全局优化算法求解该优化模型即可直接获得当前工况下天线的最佳副面位置调整参数。

式(15)的优化模型中,优化目标为非线性函数,故该优化问题为一个非线性约束优化问题,可采用可行方向法、序列二次规划法、遗传算法等优化算法进行优化模型求解,进而可在可行域中获得一组最优的副面调整量参数,即dQ*。

5.2 全仰角副面位置实时调整模型

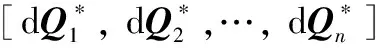
w=a+b·cos(el)+c·sin(el)

(16)

式中,el表示仰角;w表示该仰角下副面位置调整量参数(Δxs,Δys,Δzs,Δφx,Δφy);a、b、c为系数。对于6个副面位置调整量参数根据式(16)对天线不同仰角下的副面最佳位置参数分别进行曲线拟合,求出副面调整参数(Δxs,Δys,Δzs,Δφx,Δφy)在全仰角下的拟合曲线的系数a、b、c,进而获得副面全仰角实时副面调整模型。写出矩阵形式为

W=A·L

(17)

式中,A=[abc];L=[1 cos(el) sin(el)]T。

6 仿真案例与结果分析

为验证本文所提出的副面实时调整方法的正确性和有效性,本节以某26 m卡塞格伦天线为对象,探讨本文副面实时调整方法对天线结构变形后电性能的改善效果。对于文章所采用的方法而言,需获得当前工况下的天线远场电性能数据,这里通过有限元仿真模拟天线的重力变形情况,采用高斯积分计算机电耦合模型进而获得天线的远场电性能数据。

6.1 算例说明

以用于射电天文观测的26 m射电望远镜为分析对象,该天线为卡塞格伦形式结构,主面直径为26 m,副面直径为2.6 m,主面焦距为7.5 m,其几何参数示意图如图6所示,常用工作频段为c波段,频率5 GHz,波长0.06 m。该天线的馈源对口径面的照射为高斯型分布,其边缘照射电平为-12 dB。天线最佳预调角为40°。

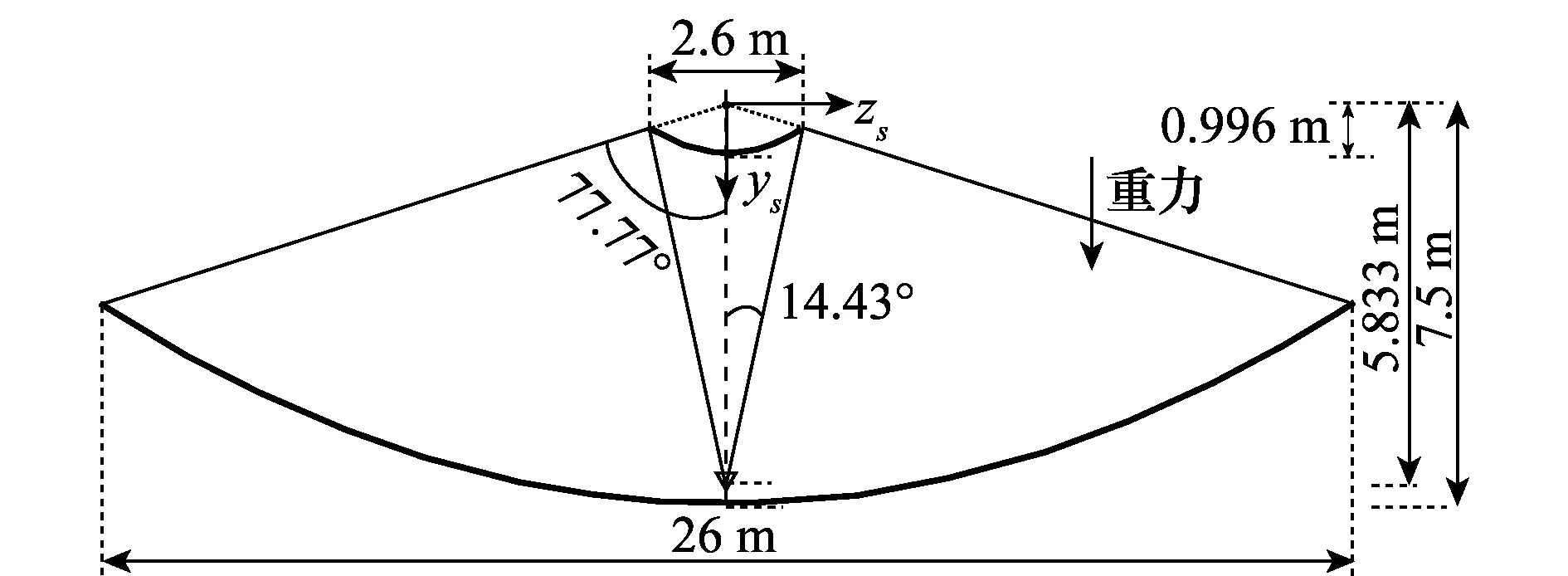
图6 26 m射电望远镜天线几何参数示意图Fig.6 26 m antenna geometry diagram

为了获得天线结构受重力载荷的影响情况,对天线主反射体指向10°、20°、35°、45°、60°、70°、80°仰角(指平为0°,仰天为90°)的天线结构进行静力分析,26 m天线和其反射体有限元模型如图7所示,通过仿真分析获得了主面变形和副面位置误差(卡塞格伦天线馈源位于反射面顶点附近,其位置误差很小可忽略)。

为了实现天线在全仰角范围内进行副面实时位置调整补偿,应用式(16)对不同仰角下的副面最佳位置调整量进行拟合,获得全仰角范围内最佳位置调整参数的数学模型。在实际工程中,通过控制调整机构对副面进行实时位置调整。

6.2 计算与结果分析

应用副面位置调整量与远场的关系模型式(14)和副面位置调整量优化模型式(15),针对26 m天线建立副面位置调整优化模型。本例中考虑到副面旋转调整可通过横向和纵向调整进行等效,故只对副面横向和纵向平移调整位置进行优化,副面位移调整范围为:沿x和z方向≤±50 mm,沿y方向≤±80 mm。

图7 26 m天线反射体结构Fig.7 26 m antenna reflector structure

采用可行方向法对天线指向10°、20°、35°、45°、60°、70°、80°仰角时的副面最佳位置参数进行优化计算。计算后的结果如表1和图8～图10所示,其中表1为天线指向7个不同仰角时副面最佳位置调整量及调整前后电性能参数比较,图8～图10为天线指向10°、45°和80°仰角时的副面调整前后的远场增益方向图。表1中,G1为副面调整前天线增益,G′为副面调整后天线增益,η1为副面调整前天线效率,η′为副面调整后天线效率。

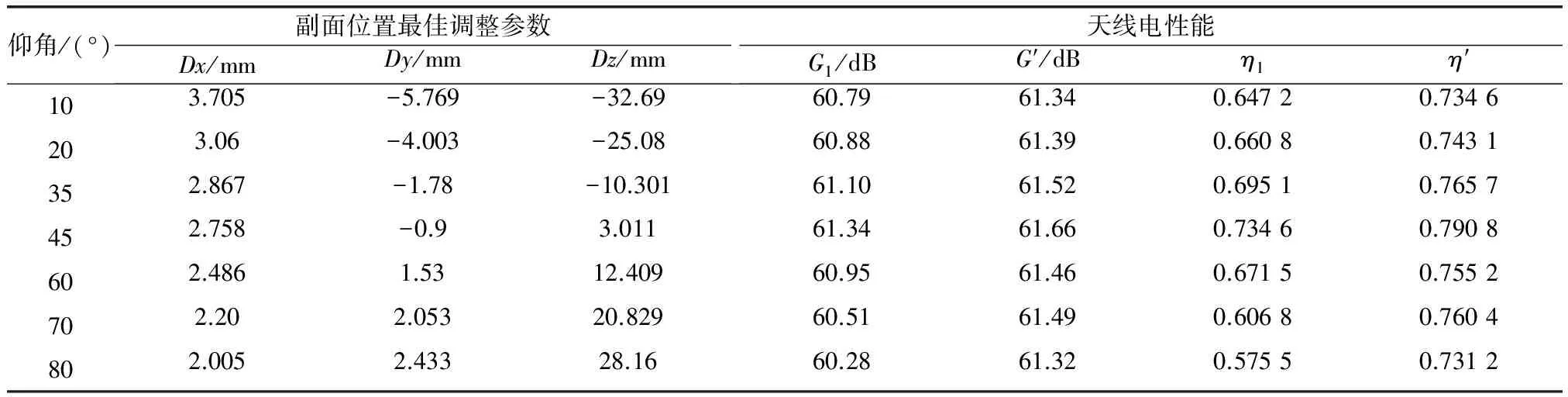
表1 26 m卡塞格伦天线各仰角下副面调整参数及其电性能比较

由表1中各仰角的副面位置最佳调整参数可知,副面沿z方向调整长度比沿x和y方向较大,这主要由于天线主反射体指向不同仰角时,背架的结构变形是非均匀的,其副面支撑相当于悬臂梁支撑,副面所受的重力载荷引起的变形在垂直于支撑方向相对较大,即z方向,故沿z方向的副面调整量也较大。由于天线反射体采用了保型设计,其背架为圆对称结构,其重力变形后的曲面与最佳吻合抛物面误差最小,其焦距的变化量不大,故副面沿y方向的调整量不大。此外，由于副面沿俯仰平面的结构变形近似呈最优对称,故副面沿x方向调整量很小。

由图8～图10可知,副面调整前方向图恶化比较严重,副瓣较高且呈现出左右不对称情况,主瓣宽度较大,由此可看出，天线背架和副面支撑的重力变形引起了严重的电性能下降,其副面位置存在横向偏差和纵向偏差;通过副面位置优化调整后,方向图得到了较大改善,主瓣峰值明显提高,副面电平降低,且呈现出左右对称情况,这表明天线副面位置的横向偏移和纵向偏差都已经得到补偿,天线的电性能有了很大提高。

图8天线指向10°仰角时,俯仰扫描方向图呈现出左右明显不对称情况,且左侧副瓣电平比右侧副瓣电平高,由此可判断副面位置向方向图中心的左侧(即低仰角方向)偏移,应将副面向高仰角方向进行横向位置调整,即沿z轴负方向调整,这与副面位置优化后的结果(表1中10°仰角时副面调整Dz=-32.69 mm)相一致。副面调整后,副瓣电平左右不对称情况减小,主瓣峰值提高,方向图得到了明显改善。同理，图10天线指向80°仰角时,俯仰扫描方向图呈现右侧副瓣电平比左侧副瓣电平高,则副面向高俯仰方向偏移,应将副面向z轴正方向进行调整。对副面位置优化后,其最佳调整参数为Dz=28.16 mm,该调整方向与之前方向图分析一致。

图8 10°仰角副面调整方向图Fig.8 Antenna gain pattern at 10° elevation angle after subreflector adjustment

图9 45°仰角副面调整方向图Fig.9 Antenna gain pattern at 45° elevation angle after subreflector adjustment

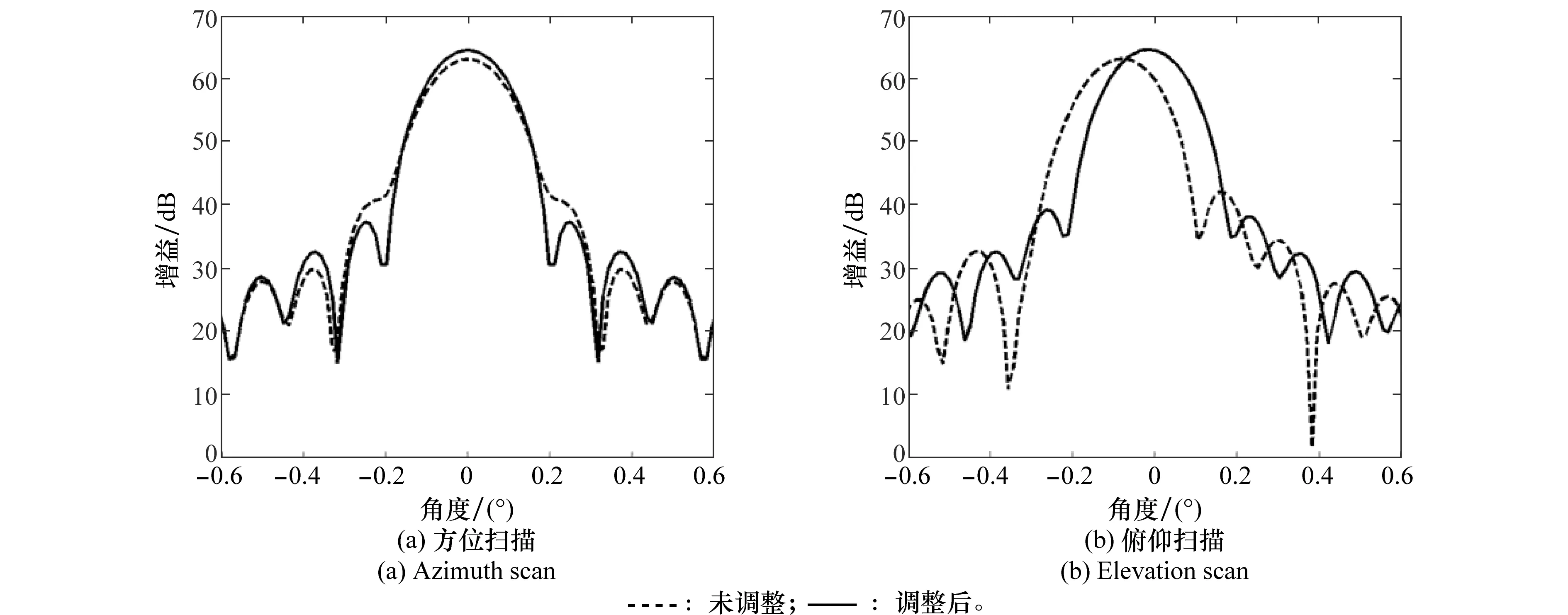
图10 80°仰角副面调整方向图Fig.10 Antenna gain pattern at 80° elevation angle after subreflector adjustment

由上述结果分析可知,通过本文所述的以电性能为目标的副面位置优化计算,能够对因结构重力变形影响导致的电性能衰减进行改善和补偿,由此可进一步表明，本文所述副面位置调整方法的正确性与有效性。

为了实现天线在全仰角范围进行实时副面调整,基于全仰角副面位置调整模型式(16)对 表1中多个仰角时的不同副面位置最佳调整参数进行拟合,其拟合结果如表2所示,在全仰角范围内副面位置调整可根据仰角el和模型系数向量B获得不同参数的调整量,进而驱动副面使其位于最佳电性能位置,实现副面实时调整。

天线在实际工作过程中会受到多种环境载荷的影响(如重力、温度、风荷等)而产生结构变形误差,但在诸多变形误差源中重力变形起主导作用,且为系统误差,故本文只考虑了对重力变形误差的补偿,实际天线工作过程中其电性能会由于其他环节因素的影响而进一步下降,这将对副面调整的效果产生一定的影响。

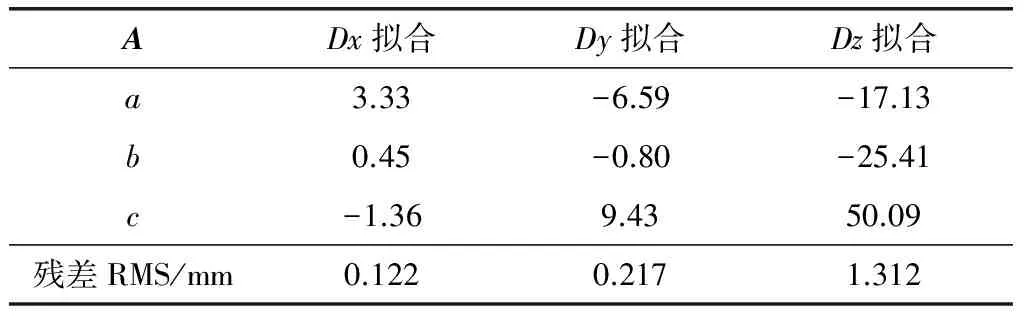
表2 全仰角副面位置实时调整模型系数

7 结 论

为了更加快速便捷地确定副面的最佳位置,从机电耦合角度出发,建立了双反射面天线副面位置调整量与远场方向图的关系式,使副面位置与天线电性能间建立了直接联系,进而使以电性能为目标的副面位置调整得以实现;基于最优化理论,以天线相对增益最优为目标对不同仰角时的副面位置最佳调整量进行了优化计算,其结果表明通过副面位置优化后天线电性能有了较大改善;对多个仰角的副面最佳位置调整参数进行了拟合,基于全仰角副面位置实时调整模型,获得了在全仰角范围内天线结构重力变形后的副面位置最佳调整参数,进而可实现全仰角范围的副面位置实时调整。

[1] 段宝岩. 电子装备机电耦合研究的现状与发展[J]. 中国科学: 信息科学, 2015,45(3): 299-312.

DUAN B Y. The present situation and the development of electronic equipment electromechanical coupling research[J]. Scientia Sinica Informationis, 2015,45(3): 299-312.

[2] 王娜. 新疆奇台110米射电望远镜[J]. 中国科学:物理学 力学 天文学, 2014,44(8): 783-794.

WANG N. Xinjiang Qitai 110 meter radio teles-cope[J]. Scientia Sinica Physica, Science China Physics, Mechanics & Astronomica, 2014,44(8): 783-794.

[3] 叶尚辉. 天线结构设计[M]. 北京:国防工业出版社, 1980.

YE S H. Antenna structure design[M]. Beijing: National Defense Industry Press, 1980.

[4] HOERNER S V. Design of large steerable antennas[J]. Astronomical Journal, 1967, 72(72): 35.

[5] IMBRIALE W A. Distortion compensation techniques for large reflector antennas[C]∥Proc.of the Aerospace Conference, 2001: 799-805.

[6] BOLLI P, OLMI L, RODA J, et al. A novel app-lication of the active surface of the shaped sardinia radio telescope for primary-focus operations[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13(1): 1713-1716.

[7] 王从思, 李江江, 朱敏波, 等. 大型反射面天线变形补偿技术研究进展[J]. 电子机械工程, 2013,29(2): 5-10.

WANG C S, LI J J, ZHU M B, el al. Review of surface deformation compensation methods for large reflector antennas [J]. Electro-Mec-hanical Engineering, 2013,29(2): 5-10.

[8] 宋立伟, 段宝岩, 郑飞. 反射面表面与馈源误差对天线方向图的影响[J]. 系统工程与电子技术, 2009, 31(6): 1269-1274.

SONG L W, DUAN B Y, ZHENG F. Effects of reflector errors and phase center errors of feed on the far-field pattern of reflector antennas[J]. Systems Engineering and Electronics, 2009, 31(6):1269-1274.

[9] 连培园,段宝岩,王伟,等.远场反推变形反射面天线馈源调整量[J].西安电子科技大学学报:自然科学版,2014,41(5):105-111.

LIAN P Y, DUAN B Y, WANG W, et al. Inverse derivation of the adjustment quantity of the distorted reflector antenna feed from a far field[J]. Journal of Xidian University (Natural Science), 2014,41(5): 105-111.

[10] 冷国俊, 王伟, 段宝岩,等. 赋形卡氏天线主面变形的副面实时补偿[J]. 系统工程与电子技术, 2011, 33(5): 996-1000.

LENG G J, DUAN B Y, WANG W, et al. Subreflctor real-time compensation for main reflector deformation of shaped Cassegrain antenna[J]. Systems Engineering and Electronics, 2011, 33(5): 996-1000.

[11] WANG W, WANG C, DUAN B, et al. Compensation for gravity deformation via subreflector motion of 65 m shaped cassegrain antenna[J].IET Microwaves Antennas & Propagation,2014,8(3):158-164.

[12] 段宝岩. 电子装备机电耦合理论、方法及其应用[M]. 北京:科学出版社, 2011.

DUAN B Y. Electronic equipment electromechanical coupling theory, method and application[M]. Beijing: Science Press, 2011.

[13] RUZE J. Antenna tolerance theory—a review [J]. Proceedings of the IEEE, 1966, 54(4): 633-640.

[14] ZARGHAMEE M. Peak gain of a cassegrain antenna with secondary position adjustment[J]. IEEE Trans.on Antennas & Propagation, 1982, 30(6):1228-1233.

[15] LEVY R. Structural engineering of microwave antennas: for electrical, mechanical, and civil engineers[M]. Piscataway, NJ: IEEE Press, 1996.

[16] RICHARD M P, DANA S B. Systematic errors in the empirical focus tracking model[EB/OL]. [2017-02-20]. http:∥wwwlocal.gb.nrao.edu/ ptcs/ptcspn/ptcspn18/ptcspn18.pdf?origin=publication_detail.