中国农业增长空间效应研究

王金田, 高 峰, 高 勇

(山东理工大学 经济学院，山东 淄博 255000)

一、引言

改革开放以来，中国农业经济获得了巨大成功，虽然农业在国内生产总值中的比重由28.4%下降到10%，但这并没有改变农业在国民经济中的基础地位。从1978年至2013年，人均粮食拥有量增长39.16%，人均拥有棉花、油料、糖料、水产品、水果、奶制品、禽蛋和茶叶等实现了成倍乃至二、三十倍增长。据国际粮农组织(FAO)统计，2012年中国谷物、小麦、稻谷、花生、籽棉、茶叶、水果、肉类、玉米等产量居世界第一位。按不变价格计算的农业增加值从1978到2013年增长629.72%，以占世界7.59%的耕地养活了19.18%的人口。增加农民收入，促进农业发展一直是中国经济社会发展的现实(韩俊，2001)[1]31-34，农业增长问题的研究一直是学者关注的重点。

研究农业增长的文献很多，主要涉及以农业产值或农业生产率为被解释变量，各种投入要素为解释变量的模型，如实物投入、技术、制度等(于晓华和赵国庆，2009)[2]68-74，制度的影响(Lin，1992[3]34-51；乔榛等，2006[4]73-82)，此外，还有非市场的土地再分配和土地确权(Klaus Deininger et al.，2014)[5]505-520；基础设施(Fan and Zhang, 2004)[6]395-421；土地分割(Chen et al., 2009)[7]153-161；环境污染恶化(Monchuck et al.，2010)[8]346-354等，其共同特征是以行政区划单位，如省、区、市、县等研究中国农业增长问题，不考虑区域协调发展问题。

对于农业空间增长的文献在引入空间因素时主要考虑两种途径。

(一)将空间因素作为解释变量引入模型

Gallup et al.(1999)[9]179-232通过控制运输成本、疟疾指数、农业生产率等指标，研究位置与气侯对收入水平和收入增长的影响，结果显示距离经济核心区越远的国家收入会越低。

Duvivier(2013)[10]923-943利用Chen and Partridge(2013)[11]1313-1331的方法构造市场潜力指标作为城市邻近(Urban Proximity)指标，采取中国县级2005—2009年的数据，估计异质城市效应是否会显著增强邻近农村的技术效率，实证结果显示东部地区城市邻近会显著增强效率，而中部地区影响低，西部地区影响不显著。

(二)直接采取空间计量方法进行实证研究

其特点是在模型估计中引入空间权重矩阵。Cho et al.(2010)[12]2031-2040利用1999年中国县级农业数据，采取空间滞后模型分析劳动力、农业机械总动力、化肥和灌溉等如何影响农业产值，实证结果表明空间因素对农业产值的影响关系显著为正。

许祯育和张宏浩(2010)[13]79-107利用2005年台湾村级数据，采取空间滞后(Spatial Lag)和空间误差(Spatial Error)模型对农业收入问题进行研究，实证结果显示空间滞后和空间误差的溢出效应系数值分别为0.324和0.052，结果显著，说明空间溢出对农业增长具有正向影响关系。

Ulimwengu and Sanyal(2011)[14]使用面板数据的空间Durbin模型，利用1961—2006年撒哈拉以南非洲地区48个国家的数据，分析化肥、牲畜、拖拉机、劳动力和土地质量等对农业产出的影响，实证结果显示正向显著的农业溢出效应存在，每个国家平均可以因溢出获得2.5%的增长。

Yu et al.(2014)[15]279-290使用2000年和2007年土耳其的分省农业数据，采取空间Durbin模型实证研究劳动力、农业机械和化肥变量对农业产出的影响，结果表明农业活动差异和地理条件影响要素投入的回报，农业增产政策的制定须考虑基于农业部门的空间异质的区域比较优势。

此外，Gutierrez and Sassi(2012)[16]9-38，运用Barro类型的收敛模型，采取空间滞后模型估计农业收敛性问题，结果显示系数为0.2295，具有显著性，即对于欧洲农业增长而言空间因素会加速农业收入的收敛性。

由于在实际生产活动中常出现跨越行政区划界限的现象，比如劳动力流动、知识和创新的传递或扩散、相邻地区的空间邻近性等，农业经济等会受相邻地区的影响，在实证研究中如果省略重要变量将导致参数估计结果有偏和不一致，在空间面板固定效应模型估计中同样存在此问题。因此，我们将该因素引入模型，基于空间计量方法研究农业增长问题。当前研究多集中于国家和省级层面数据，对于中国县域经济中农业增长的研究较少；另外，在农业增长研究中较少关注内生性给估计带来的偏差和空间计量模型选择问题。

因此，构建农业增长的空间因素理论模型，采用中国1995—2011年1590个县的数据，通过空间面板模型估计农业增长问题，结合“地理邻近”权重矩阵和“经济邻近”权重矩阵研究农业增长的溢出效果(Spillover Effect)，并考虑内生性问题。最后，我们发现：通过内生性的判断，发现农业机械总动力不存在内生性；从整体上看，中国农业增长中存在溢出效应，且扩散效应(Diffusion Effect)大于集聚效应(Agglomeration Effect)，即溢出效应为正，而且能够贡献1%以上的作用，拉动农业增长0.1个百分点。

本文的价值体现在二个方面：一是数据方面，中国农业增长空间分析中较少采取连续性面板县域数据，本文选取1995—2011年县级数据；二是实证方法方面，采用空间面板Moran类型检验及空间Durbin模型的选择。

二、理论分析框架

遵循Alesina, Angeloni and Etro(2001)[17]与Ulimwengu and Sanyal(2011)的模型分析框架，假设有经济基础相同(包括收入等)而偏好不同的N个行政单元，其人口大小标准化为1。一般意义上，考虑分析行政单元的交互作用，即考虑策略替代(Strategic Substitutes)、私人消费和公共支出是埃奇沃思不相关(Edgeworth-independent)，第i个行政单元有如下的拟线性(Quasi-linear Utility Function)效用函数：

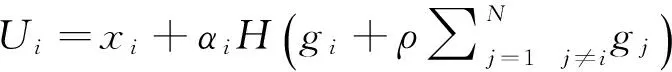
(1)

这里Ui表示第i个行政单元的效用，xi为私人消费，gi是公共支出，如基础设施、公共投资或国防等，H(·)表示行政单元i的公共支出效用，这里H’(·)>0和H’’(·)<0，i外生非负，表示行政单元i公共消费相比私人消费的重要程度指标，可代表行政单元i的偏好，并假定指标可观测，不失一般性假定1<2<…N。因为政府支出是公共品(Public Goods)，公共品具有非排他性(Nonexclusion Properties)、外溢性(Spillover)和供给的规模经济(Economies of Scale)，[0,1]表示其它的行政单元(不包括第i单元)对第i单元的外溢效果。

为简单起见，根据Caldeira, Foucault and Rota-Graziosi(2012)[18]的方法，为阐述简单，假定忽略地方政府债务问题，考虑如下预算约束：

yi=xi+c(gi)

(2)

这里yi表示行政单元i的收入，c(gi)表示提供gi数量公共品的成本，成本函数假定是增函数和凸函数：c’(·)>0和c’’(·)<0，凸函数属性反映递增的公共品边际成本；同时，由于研究集中于当前支出(Current Spending)而不是公共投资(Public Investment)，这样将方程(2)带入方程(1)，得到如下方程(3)，该目标函数的取值依赖于策略变量(g1,…,gi,…,gN)：

(3)

每个行政单元选择自己的公共品支出，同时考虑其它行政单元的支出水平，该博弈是一个静态Nash均衡。

考虑如下两种情形：

(一)各地区之间的关系独立

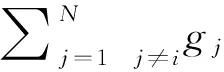
∂Ui/∂gi=-∂c(gi)/∂gi+

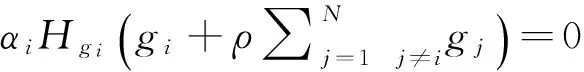
所以有：

(4)

由上可见，等号右端项是关于i地区成本函数的偏导数，等号左端包括i地区和其它j(ji)地区，除非=0，则等号左右两端存在非对称情形，即说明来自方程(4)的Nash均衡解是非有效的。

(二)各个地区之间存在相互联系

则可以得到如下结果：

(5)

方程(5)的解是有效的，因为其包含了溢出效果。因此，评估中国农业增长的空间效应关键之处是估计溢出效应系数。

三、计量模型和数据说明

(一)计量模型

为了实证测算中国县级农业增长的空间效应，进行空间实证分析，将空间因素引入模型。首先考虑空间自相关是否存在，即引入外溢性是否合理，考虑Mutl and Pfaffermayr(2010)[19]225-228空间面板的Cliff and Ord Moran’s I与LM检验，如果通过检验，基于上述理论框架，我们借鉴Ulimwengu and Sanyal(2011)模型，选取如下的Cobb-Douglas生产函数。

空间Durbin模型表示为：

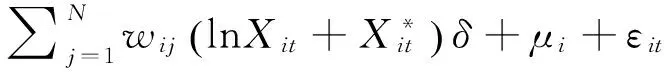
(6)

这里，i表示各县市，i=1,…,N，t表示时间，t=1,…,T。lnyit是第i个县第t年第一产业增加值的对数形式；lnXit为第i个县第t年的解释变量，是K11阶的列向量，Xit*是其取值可能存在负值的变量，是K21阶的列向量，K1+K2=K；it～IID(0,2)；i表示空间个体效应。如果i与某个解释变量相关，则称为固定效应模型(FixedEffect，FE)，在这种情况下，OLS是不一致的。如果i与所有解释变量都不相关，则称为随机效应，称为空间自回归系数，wij是空间权重矩阵W的元素，假定W是预先设置的非负的矩阵，并且W进行了行标准化处理，空间滞后模型典型考虑空间或社会交互过程，一种内生的交互作用。

1．权重矩阵设置

“地理临近”型权重矩阵W的选择。由于文中数据选择了中国1590个县，存在数据缺失现象，门限权重矩阵对模型估计带来的不足可能更大，因此W选择“地理临近”型矩阵，考虑k邻居权重矩阵。定义每个空间单元i到所有空间单元ji的距离，并排序dij(1)dij(2)…dij(N-1)，这里的距离为Haversine距离*http://en.wikipedia.org/wiki/Haversine_formula。对每个k=1,…,N-1，定义集合Nk(i)={j(1),J(2),…,j(k)}包含距离i最近的k个单元。对于每个k，最近k邻居形式如下：

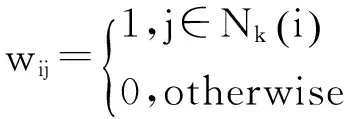
关于最优k的选取，McLachlan(2004)建议选取N2/8或N3/8，本研究选取N2/8kN3/8，根据样本量(1595个)选取的k为7-15，在具体估计判断时取中间值k=11。

2．空间计量模型选择

一是Wald和LR检验。面板数据的空间计量模型通常分为固定效应的空间滞后模型，固定效应的空间误差模型，随机效应的空间滞后模型，随机效应的空间误差模型等，其可以作为固定效应和随机效应模型的扩展；对于采取空间Durbin模型还是采取SLM或者SEM则可以通过Wald检验或者LR检验进行判断，如果通过显著性水平的检验，则采取空间Durbin模型，如果没有通过显著性的检验，则采用SLM或者SEM形式。

二是拉格朗日乘数检验LM error与LM lag检验。首先检验传统面板数据模型，通过估计获取对应残差值，此时进行LM检验，其可以分为两类：LM error(Lagrange Multiplier test for Spatial Error Dependence)和LM lag(Lagrange Multiplier test for Spatial Lag Dependence)。如果LM error和LM lag都没通过显著性水平检验，则选择传统计量经济模型估计方程；如果LM lag显著而LM error不显著，表示空间聚集现象是因为空间滞后过程(Spatial Lag Process)的结果，即内生交互影响(Endogenous Interaction Effect)，因此，选择空间滞后模型；相反，如果LM error显著而LM lag不显著，表示空间聚集现象是由于空间误差过程(Spatial Error Process)的结果，即误差项间的交互影响(Interaction Effect among Error Terms)，选择空间误差模型；如果LM error和LM lag都通过显著性水平检验，则需进一步进行修正的Robust 检验，如果Robust LM error显著，则选择空间误差模型，如果Robust LM lag显著，则选择空间滞后模型。

(二)数据来源及变量说明

由于《中国县域统计年鉴》, 从2013年起不再公布乡村从业人员，且农业化肥使用部分地区公布实物量而非折纯量等原因，因此，本研究最终使用1995—2011年中国1590个县级数据研究中国农业空间增长问题，样本容量为27030个*数据来源于《中国县(市)社会经济统计年鉴》(2001—2012)，《中华人民共和国全国分县市人口统计资料》(1995—2011)，《中国县(市)社会经济统计概要2000》，《中国民政统计年鉴》(2012)，各省级(含自治区，直辖市)统计年鉴，各地市县级统计年鉴，此外气温和降雨量的数据来源于国家气象中心。。被解释变量为第一产业的增加值(lnyit)，解释变量共六个，分别包括农业机械总动力(lnTAMP)、乡村从业人数(lnNRL)、农用化肥使用折纯量(lnACCF)、农作物播种面积(lnTSA)、气温(Temp)和降雨量(Pre)*1995—2008年的平均气温，最高气温和最低气温的站点数为594个，降雨量的站点数为713个，2009—2011年的平均气温，最高气温，最低气温和降雨量采用了823个站点。对于气温，本研究采用Anusplin软件和CGIAR 90米的SRTM 4.1得到栅格数据，降雨量采取克里格(Kriging)内插法对降雨量站点数据进行插值，然后提取数据得到各县的气温和降雨量资料。。此外，由于缺少县级层面第一产业增加值价格指数，我们对此并未进行平减指数处理。

四、实证分析

(一)模型选择

在分析空间数据时，第一个步骤是确定模型的正确设定形式。这里有两个主要选择方法：一是Hendry方法；二是经典方法(Florax, Folmer and Rey, 2003)。Hendry方法通过一系列检验，遵循从一般到特殊的过程选择合适模型，而经典的方法使用“从特殊到一般”的方法。空间计量模型几乎都选取经典方法，Florax et al.通过DGP模拟，结果表明空间自回归系数大于0.7，小样本且空间自回归系数等于0.1，N=400且空间自回归系数大于0.3时，两种方法是一致的，其它情形下经典方法优于(Outperform)Hendry方法，因此，本文在选取模型时同样采取经典方法。

表 1 面板数据空间依赖性的检验

PanelMoran’sIPanelLMAverageMoran’sI统计值P-value统计值P-value统计值P-valuek邻居权重矩阵123.760.00179.780.000.40060.00

注：Panel Moran’s I为空间面板Cliff and Ord Moran’s I检验，Panel LM为空间面板LM检验，Average Moran’s I为截面Moran’s I的平均值。

空间面板数据的空间依赖性检验。采取固定效应面板数据方法估计模型，得到残差值，对该残差值选取Mutl and Pfaffermayr(2010)空间面板Cliff and Ord Moran’s I检验和LM检验。表1报告了“地理邻近”的k邻居权重矩阵(邻居数=11，其他学者如Lesage(2014)选取了8、10、12个)，检验统计量和P-value，结果表明模型存在正外溢性；此外，由于Mutl and Pfaffermayr(2010)检验统计量的取值范围并非[-1,1]，我们根据截面Moran’s I 检验统计量计算了1995—2011年的统计值，然后取17年的平均值作为统计值，计算得到P-value，结果见表1，结果也是模型存在空间依赖，因此，在模型估计中应该引入空间因素。

(二)实证结果

利用1995—2011年中国1590个县级面板数据，通过前面的识别和检验发现应考虑空间外溢性因素，因此，采取空间面板数据的估计法研究中国农业增长问题，下面实证研究理论模型中的外溢效果。

研究基于“地理邻近”权重矩阵K-NN权重矩阵估计方程(6)。据Wald spatial lag Test, LR spatial lag Test, Wald spatial error Test和 LR spatial error Test检验结果都显著，说明应该选择Spatial Panel Durbin模型。对于选择固定效应模型还是随机模型，根据Spatial Hausman检验结果应选择固定效应模型。Lee and Yu(2010)讨论了任意空间模型的标准估计问题，当个体较多而时间较少时，采取固定效应模型估计参数将导致方差的不一致和参数不一致，本文借鉴Elhorst(2014)采取的Bias Correction方式估计模型。在控制县市个体和年份固定效应下，基于“地理邻近”权重矩阵，可得表2第三列，为了便于模型比较，文中也对经典面板数据进行了估计。

表2报告了在控制时间和个体效应下，选择k=11邻居权重矩阵，其外溢性系数为0.6359，并且都通过了显著性水平检验，说明1590个县市存在正向外溢性，扩散效应(Diffusion Effect)大于集聚效应(Agglomeration Effect)。 此外，农业机械总动力、农村劳动力、农用化肥、农作物播种面积对农业增长的作用都是正的，都通过1%的显著性水平检验，气温对农业增长的影响是正的且显著，而降雨量影响是负的，通过显著性水平，可能原因是降雨可能会通过江河很快流走，导致该系数为负，且数值较小，农田用水基本要靠引水灌溉，实证结果与Zhang and Carter(1997)[20]1266-1277、邓琨(2012)[21]193-196等类似。在两种权重矩阵下数值相近，这一定程度上说明结果稳健。此外，本研究也用固定效应方法估计了经典面板数据模型，结果前五个指标都是显著正值，而气温和降雨量指标都不显著。从两个估计结果的拟合优度看，空间面板数据的拟合优度明显高于经典面板的固定效应估计，从侧面说明空间计量方法更有效。

表 2 基于“地理邻近”权重矩阵的农业空间面板增长估计

经典面板的FEK-NN权重矩阵lnTAMP0.0736***0.0700***(16.66)(15.87)lnNRL0.1693***0.1664***(19.81)(20.10)lnACCF0.0589***0.0380***(20.19)(13.30)lnTSA0.1861***0.1833***(32.33)(30.78)Temp0.00340.0147**(0.83)(2.04)Pre5.72e-06-0.00002*(0.94)(-1.90)W´lnTAMP-0.0466***(-5.98)W´lnNRL-0.1129***(-7.24)W´lnACCF0.0082(1.54)W´lnTSA-0.1184***(-11.82)W´Temp-0.0138*(-1.66)W´Pre0.00002*(1.81)W´lnVPI0.6359***(92.64)县市固定效应控制控制年份固定效应控制控制R20.75840.9745WaldspatiallagTest295.31***LRspatiallagTest302.88***WaldspatialerrorTest52.39***LRspatialerrorTest56.77***HausmanTest611.96***1993.61***样本容量2703027030

注：R2表示估计结果的可决系数。Wald spatial lag Test, LR spatial lag Test, Wald spatial error Test和 LR spatial error Test表示选择空间Durbin模型还是选择SLM或SEM的四种检验，*、**、***分别表示10%、5%、1%的显著性水平。Hausman Test表示经典或空间面板数据模型固定效应与随机效应的选择。

五、结论

在Alesina，Angeloni and Etro(2001)、Caldeira，Foucault and Rota-Graziosi(2010)与Ulimwengu and Sanyal(2011)研究基础上扩展了其理论模型，探究外溢性对农业增长的影响，基于1995—2011年1590个县的数据实证研究中国农业增长空间效应测算。我们采用空间依赖性检验，检验结果表明存在空间依赖，通过Wald、LR和Hausman检验表明本文选择空间面板Durbin模型的固定效应方法更合适。

通过实证分析，我们发现在“地理邻近”权重矩阵下，在控制个体和时间效应后，农业增长存在正向外溢性，其外溢性系数为0.6左右，都通过了显著性水平检验。实证结果说明，对于政府部门而言，在制定政策时应考虑邻居效应对农业增长的影响。目前中国县市空间邻居影响农业增长的程度还不高，说明还有较大潜力进一步拉动农业增长，持续提高农民收入。未来政府部门在制定政策时应需考虑的一个重要问题是应考虑各县市之间的空间邻近性，同时注意因为劳动力流动、技术扩散等的积极刺激作用，打破行政区划限制，破除人为自然地理行政分割限制，考虑地区比较优势，积极考虑溢出带来的增长效果，进行跨区域整合。

[1]韩俊. 关于增加农民收入的思考[J].新视野, 2001, (1).

[2]于晓华, 赵国庆. 中国农业增长研究述评[J]. 经济理论与经济管理, 2009, (4).

[3]Y., L. J. Rural Reforms and Agricultural Growth in China [J].American Economic Review, 1992, (1).

[4]乔榛, 焦方义, 李楠. 中国农村经济制度变迁与农业增长——对1978—2004年中国农业增长的实证分析[J]. 经济研究, 2006, (7).

[5]Deininger, K., Jin, S., Xia, F., & Huang, J. Moving Off the Farm: Land Institutions to Facilitate Structural Transformation and Agricultural Productivity Growth in China [J].World Development, 2014, (59).

[6]Fan, S., Zhang, L., and Zhang, X. Reforms, Investment, and Poverty in Rural China [J].Economic Development and Cultural Change, 2004, (2).

[7]Chen a, Z., Huffman, W. E., and Rozelle, S. Farm technology and technical efficiency: Evidence from four regions in China [J].China Economic Review, 2009, (2).

[8]Monchuk, D. C., Chen, Z., and Bonaparte, Y. Explaining production inefficiency in China’s agriculture using data envelopment analysis and semi-parametric bootstrapping [J].China Economic Review, 2010, (2).

[9]Gallup, J. L., Sachs, J. D., and Mellinger, A. D. Geography and Economic Development [J]. International Regional Science Review, 1999, (2).

[10]Duvivier, C. Does Urban Proximity Enhance Technical Effciency? Evidence From Chinese Agriculture [J]. Journal of Regional Science, 2013, (5).

[11]Chen, A., and Partridge, M. D. When are Cities Engines of Growth in China? Spread and Backwash Effects across the Urban Hierarchy [J]. Regional Studies, 2013, (8).

[12]Cho, S.-h., Chen, Z., and Poudyal, N. C. Spatial structure of agricultural production in China [J]. Applied economics, 2010, (6/7).

[13]许祯育, 张宏浩. 台湾农家之农业所得的空间相关性分析[J]. 农业经济丛刊, 2010, (1).

[14]Ulimwengu, J., and Sanyal, P. Using a Spatial Growth Model to Provide Evidence of Agricultural Spillovers between Countries in the NEPAD CAADP Framework [DB/OL]. IFPRI Discussion Paper 01069, 2011.

[15]Yu, T.-H. E., Cho, S.-H., Koç, A. A., Bölük, G., Kim, S. G., & Lambert, D. M. Evaluating Spatial and Temporal Variation in Agricultural Output Elasticities in Turkey [J]. Agricultural Economics, 2014, (3).

[16]Gutierrez, L., and Sassi, M. Spatial and Non spatial Approaches to Agricultural Convergence in Europe [J].Economia & Diritto A groulimentare,2012,(17).

[17]Alesina, A., Angeloni, I., and Etro, F. THE Political Economy of International Unions [DB/OL]. Working Paper 8645, 2001.

[18]Caldeira, E., Foucault, M., and Rota-Graziosi, G. Decentralisation in Africa and the Nature of Local Governments’ Competition: Evidence from Benin [DB/OL]. NBER Working Paper No. 18126, 2012.

[19]Mutl, J., and Pfaffermayr, M. A Note on the Cliff and Ord test for Spatial Correlation in Panel Models [J]. Economics Letters, 2010, (2).

[20]Zhang, B., and C.Carter. Reforms, the Weather, and Productivity Growth in China’s Grain Sector [J]. American Journal of Agricultural Economics, 1997, (4).

[21]邓琨. 农业产业结构调整对农业经济增长影响的实证分析——以四川省为例[J]. 广东农业科学, 2011, (9).