Grid Methods in Computational Real Algebraic(and Semialgebraic)Geometry∗

Felipe CUCKER

(À Philippe,pour des années d’amitié)

1 Putting in Context

The primary objects of study of real algebraic geometry are real algebraic sets.These are subsets of Rndefined as zero sets offinite sets of polynomials.A naturally occurring class of sets,in the context of this study,is that of semialgebraic sets.These are subsets of Rndefined as Boolean combinations(i.e.,unions and intersections)of polynomial equalities and inequalities.Two classic books on real algebraic and semialgebraic geometry are[6,10].

The fact that polynomials are easy to describe(by,for instance,their degree and the list of their coefficients),together with their ubiquity in computational problems,motivated the blossoming of a subject,within symbolic computation(a.k.a.computer algebra),devoted to problems involving semialgebraic sets.A comprehensive monograph on this subject is[5];a recent survey is[3].

Central to this subject was the issue of computational complexity.Assume that the problem at hand takes as input a collection of s polynomials in n variables,of degrees d1,···,ds,respectively.Then the size of this input is the number of coefficients used to describe this collection.That is,this size is

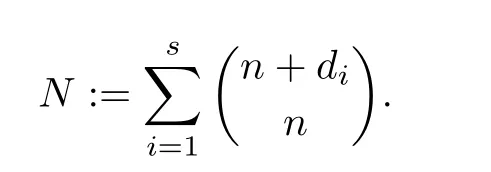
This quantity is in general exponentially large in n but it does not need to be so.For instance,in the case of systems of quadratic polynomials,N=O(sn2).

Complexity considerations were not always at the forefront in the algorithmics of semialgebraic geometry.One of thefirst remarkable algorithms in the subject was created by Alfred Tarski in the late 1930’s(see[45]1The publication of Tarski’s results was delayed by the war.).This algorithm takes as input an expression of the form

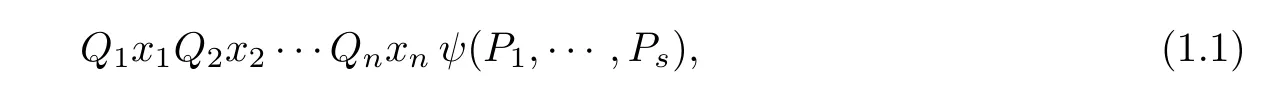
where P1,···,Psare polynomials in R[x1,···,xn],ψ(P1,···,Ps)is any Boolean combination of these polynomials,and Qjxjis a quantification either existential— ∃xj— or universal—∀xj.The fact that all variables are quantified implies that such an expression is either true or false.Tarski’s algorithm thus returns the truth value of(1.1).The focus at that time was on(theoretical)computability and Tarski’s result showed that a number of problems(which ultimately can be reduced to deciding the truth of statements as(1.1))could be,in theory,solved.In practice the situation was bleaker.The complexity of Tarski’s algorithm is of the order of

In the seventies,Collin[16]and Wüthrich[47]independently devised a method today referred to as Cylindrical Algebraic Decomposition(CAD for short).We will not describe what exactly CAD does;suffice it to say that a CAD of the collection{P1,···,Ps}allows one to decide the truth of any sentence of the form(1.1),no matter the prefix of quantifiers.The complexity of CAD,which is doubly exponential in n,

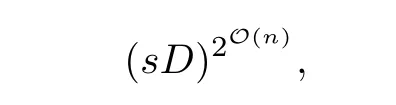
is far from practical but nonetheless much better than Tarski’s.Here D=max{d1,···,ds}.

A breakthrough was made in the late 1980’s with the introduction of the critical points method by Grigoriev and Vorobjov[27—28],and its improvements in[4,34—36]among others.This method allows one to eliminate quantifiers at a cost which is singly exponential in the number of variables n and doubly exponential only in the number ℓ of quantifier alternations in the prefix of(1.1).That is,it is of the order

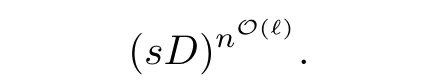
The critical points method allowed one to provide single exponential time algorithms for a number of basic problems in semialgebraic geometry.Indeed,let S be a semialgebraic sets defined via a collection{P1,···,Ps}as above.Then the problems(to mention just a few)

could all be solved within time(sD)nO(1).Among those solvable with CAD but for which no algorithm has been devised that would work within a time bound single exponential in n stands out the following:

Homology,i.e.,compute the homology groups of S.

At this point we note that these bounds may be polynomial in the input size N but may be exponentially large as well,as for the case of families of quadratics polynomials.

In 1989,Blum,Shub and Smale wrote a paper[9]adding a new twist to the complexity considerations above.They developed a theory of complexity over the reals along the lines of the(at that time blooming)discrete theory of complexity.In particular,they defined the class NPR,the real analog of the acclaimed class NP(see[15]),and they showed that Feasibility is NPR-complete.Shortly said,this means that Feasibility is universal in the class NPRin the sense that whichever algorithmic improvement(viz complexity)can be found for Feasibility the same improvement will hold for all problems in this class.Interestingly,this remains true even when we restrict all polynomials in Feasibility to be quadratic.This foundational paper gave rise to similar completeness results.In particular,Koiran[29]showed that Dimension is NPR-complete as well,and in[11]the completeness in#PR(the real analog of the classical#P)was shown for both Counting and Euler.Other complexity classes over the reals and a list of complete problems for them,all involving real polynomials,was shown in[12].

Towards the end of[9],in a list of open problems,Blum,Shub and Smale mention a theme that was going to occupy a central position in Shub and Smale research(as witnessed by the Bézout series[39—43]and by Part II in[8]).Quoting from Section 5,it would be useful to incorporate round-offerror,condition numbers and approximate solutions into our development.

The rationale behind this quote is the assumption of infinite precision in the machine model proposed in[9]:These machines are theoretically capable of store,and operate with,arbitrary real numbers.In the practice of numerical analysis,in contrast,real numbers are replaced byfloating-point numbers thus giving rise to round-off errors.These errors accumulate during the computation and the goal of stability analysis is to gauge the quality of an algorithm regarding this accumulation.Blum,Shub and Smale are thus asking to incorporate stability in the complexity theory they developed.

Central to any possible extension of this theory(see[18]for one such extension)there is the notion of condition.A condition number,associated to an input a for a problem P,is,loosely speaking,a measure of how much the outcome of P is affected by small perturbations of a.It is independent of the choice of an algorithm for solving P and thus emphasizes the role of a in the stability analysis.Condition numbers usually take values on the interval[1,∞]and inputs a for which the condition is∞are said to be ill-posed.Those are the inputs for which,no matter the algorithm used,no matter howfine its precision,there is no hope of a meaningful,reliable output.

Interestingly,condition numbers play a major role in complexity analysis as well(even assuming infinite precision).Indeed,it is common in numerical analysis to design iterative algorithms.These are procedures that,unlike those mentioned above(CAD,critical points method,···),do not have a complexity bound purely in terms of the input size but may take arbitrarily long times even when all input’s parameters(e.g.,n,s and D above)are fixed.Instead,it is common,at least within certain subjects,that the number of iterations that these algorithms perform is bounded by a function on these parameters and the condition number of the input.In particular,they may loop forever when the input is ill-posed.

Iterative algorithms and their condition-based analysis are the bread and butter of numeri-cal linear algebra(see[25,46]).They made a burst in optimization with the pioneering work of Renegar[37—38]and eventually found their way in semialgebraic geometry.An early representative of this work is[23],where an iterative algorithm for Feasibility is proposed and studied.

The motivation behind[23]is the observation that the critical points method performs few operations with large matrices.This is not only costly in time but also unlikely to be numerically stable.In contrast,an algorithm performing a large number of(independent)operations on small matrices,while equally costly in time,should at least be numerically stable.

The ideas in[23]were later extended in[19]to the Counting problem,in[22]to the Homology problem for real projective sets and in[14]to the same problem but for semialgebraic sets.In the next pages we will describe these ideas and the analyses of the resulting algorithms.

2 Setting the Tools

2.1 Spaces of polynomials

Let d=(d1,···,dm)∈ Nmbe such that di≥ 1 for all i≤ m.To such a tuple we associate the linear space Hd[m]of homogeneous polynomial systems f=(f1,···,fm)in R[X0,···,Xn]with degreefi=di.We make Hd[m]an inner product space by endowing it with the Weyl inner product.For g,h homogeneous of degree d in R[X0,···,Xn]we define

is the multinomial coefficient.This definition naturally extends to an inner product in Hd[m]which is no more than the dot product for a weighted monomial basis.The main reason to consider it is that it is invariant under the action of the orthogonal group O(n+1).That is,for all f,g ∈ Hd[m]and all u ∈ O(n+1),〈f,g〉= 〈f ◦u,g◦u〉.This invariance allows for great simplifications in many arguments.See e.g.[13,§16.1]for details.In all what follows,for f∈Hd[m],the expression‖f‖denotes the norm of f induced by the Weyl inner product.

2.2 The condition of a polynomial system at a zero

How much does a zero ξ∈ Rn+1of a system f ∈ Hd[m]move when we slightly perturb the coefficients of f?An answer to this question,the condition µnorm(f,ξ)of f at ξ,was provided by Shub and Smale in their “Bézout series” of papers[39—43].

(we write simply Δ if ξ belongs to the unit sphere Sn⊂ Rn+1).Shub and Smale defined

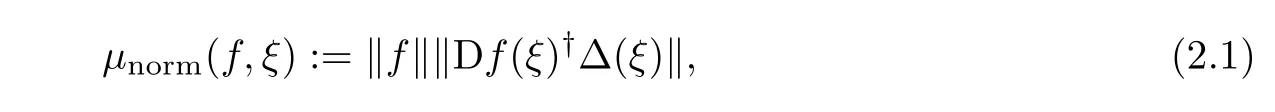
when Df(ξ)is surjective and µnorm(f,ξ):= ∞ otherwise.Here Df(ξ)†:Rm→ Rn+1is the Moore-Penrose inverse of the full-rank matrix Df(ξ),i.e.,

where Df(ξ)tis the transpose of Df(ξ).This coincides with the inverse of the restricted linear map Df(ξ)|(kerDf(ξ))⊥.Also,the norm in ‖Df(ξ)†Δ(ξ)‖ is the spectral norm.

We note that the expression on the right of(2.1)is well-defined for arbitrary points x ∈ Sn,so we can define µnorm(f,x)for any such point.This property will allow us to define,for each of the problems in Section 3,a condition number depending only on the considered problem and the data at hand which usesµnormas a basic ingredient.

Remark 2.1For any λ /=0 we have µnorm(f,x)= µnorm(f,λx),since when Df(x)is surjective,Df(λx)†=(ΛDf(x))†=Df(x)†Λ−1for

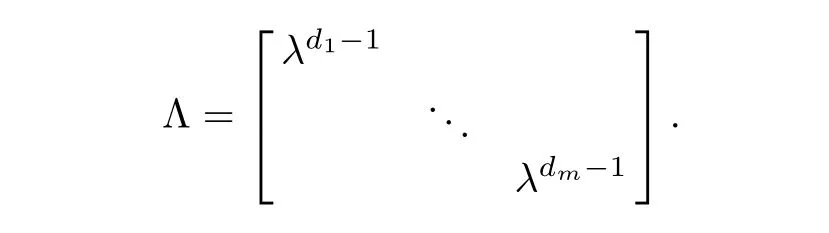
Similarly,µnorm(f,ξ)= µnorm(λf,ξ)for all λ /=0.

Finally,the following result(see[13,Proposition 19.30])allows one to estimateµnorm(f,y)by evaluatingµnorm(f,x)at a point x sufficiently close to y.

Proposition 2.1There exist constantsC＞ 0such that the following is true.For allε∈ [0,ε],allf ∈ Hd[m],and allx,y ∈ Sn,ifD32µnorm(f,y)dS(x,y)≤ Cε,then

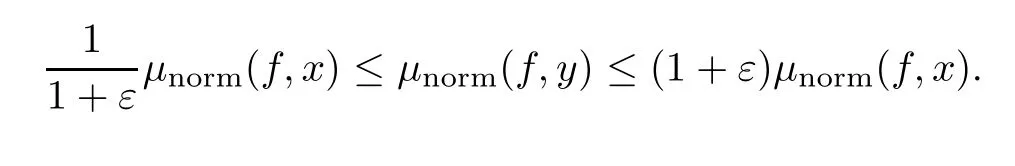
2.3 Probabilities

Recall the class of numerical algorithms we mentioned in the introduction.These are iterative algorithms whose number of iterations are analyzed in terms of the condition of the input(as well as its size).Because this condition cannot in general be estimated a priori(it is common that computing the condition of an input is as difficult as solving the problem for which this input is so)a way of gauging the efficiency of algorithms of this kind is via probabilistic estimates.To this end,the space of data is endowed with a probability measure M.Then,cost(a),the cost of an algorithm at a data a,becomes a random variable and,when possible one attempts to provide bounds for the expectation

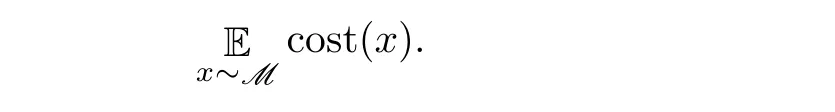
This averagecase complexity provides,more often than not,a realistic measure of an algorithm’s efficiency.But it is sometimes overly pessimistic.Indeed,there are examples of algorithms which are known to be efficient in practice but nonetheless have a large,or even infinite,average-case complexity.In a recent paper Amelunxen and Lotz[2]identified as a possible cause for this discrepancy the existence of an exceptional set of inputs on which the algorithm runs in superpolynomial time but having a measure that is vanishing exponentially fast when the dimension grows.A prototype of this phenomenon is the behavior of the power method to compute a dominant eigenpair of a symmetric matrix.This algorithm is considered efficient in practice,yet it has been shown that the expectation of the number of iterations performed by the power method,for matrices drawn from the Gaussian Orthogonal Ensemble(see[32]),is infinite[30].Amelunxen and Lotz[2]showed that,conditioned to exclude a set of measure at most 2−n,this expectation is O(n2)for n×n matrices.The moral of the story is that the power method is efficient in practice because it is so in theory if we disregard a vanishingly small set of outliers.This conditional expectation,in the terminology of[2],shows a weak average polynomial cost for the power method.More generally,we will talk about a complexity bound being weak when this bound holds out of a set of exponentially small measure.

Our probabilistic analyses in Section 3 rely on a fact observed by Demmel[24]namely,that condition numbers are often bounded by the normalized inverse of the distance to the nearest ill-posed problem.For quantities defined in this way,usually referred to as conic condition numbers,the following result(see[13,Theorem 21.1])is useful.We rephrased the statement in terms of the isotropic Gaussian distribution instead of the uniform distribution on the sphere.The scale invariance of the statement makes both formulations equivalent.

Theorem 2.1LetΣ⊆Rp+1be contained in a real algebraic hypersurface,given as the zero set of a homogeneous polynomial of degreedand leta∈Rp+1be a centered isotropic Gaussian random variable.Then for allt≥(2d+1)p,

2.4 Numerical stability for discrete-valued problems

Recall,the machine precision of a finite-precision algorithm is a number εmach∈ (0,1)such that the result x of any operation performed by the algorithm is replaced by another number~x satisfying~x=x(1+δ)for some δ with|δ|≤ εmach.The quantity log2εmach,basically,indicates the number of bits in the mantissa of afloating-point representation of real numbers in the execution of A.

Algorithms computing a continuous function of their input have a standardfinite-precision analysis estimating how much may the error of the output be for a given εmach.But for problems having only a discrete set of values another form of analysis is necessary.The template result below is the most common such form.

Template ResultLet A denote a(fixed-precision)algorithm that,with infinite precision,computes a function ϕ :D → Rq.Let Aϕdenote the function computed by A withfinite precision.Finally,let condϕ(a)denote the condition number of an input a∈ D.If

then Aϕ(a)= ϕ(a).Here size(a)denotes the size(given by one or more integers)of data a and g is a function of this size and the condition of a.

2.5 Newton’s method and point estimates

Let f:Rn+1→Rm,m≤n+1,be analytic.The Moore-Penrose Newton operator of f at x ∈ Rn+1is defined(see[1])as

We say that it is well-defined if Df(x)is surjective.

Definition 2.1Letx∈ Rn+1.We say thatxis an approximate zero offif the sequence(xk)k≥0defined asx0:=xandxk+1:=Nf(xk)fork ≥ 0is well-defined and there exists a zeroζoffsuch that,for alli≥ 0,

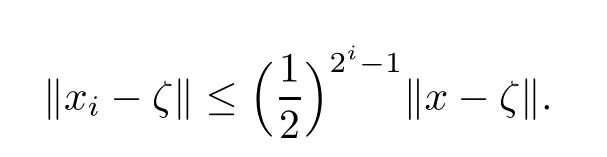
The pointζis said to be the associated zero ofx.

Following ideas introduced by Steve Smale[44],the following three quantities are associated to a point x∈Rn+1(see[43]):

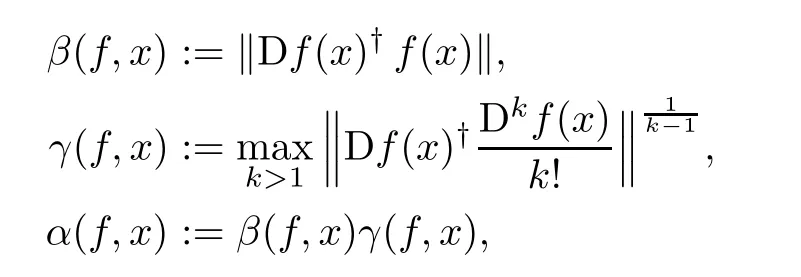
when Df(x)is surjective,and α(f,x)= β(f,x)= γ(f,x)= ∞ when Df(x)is not surjective.The quantity β(f,x)= ‖Nf(x)− x‖ measures the length of the Newton step at x.The value of γ(f,ξ),at a zero ξ of f,is related to the radius of the neighborhood of points that converge to the zero ξ of f,and the meaning of α(f,x)is made clear in Theorem 2.2 below.

In this survey we are interested in the theory of point estimates for polynomial maps f=(f1,···,fm).When the fiare homogeneous,the invariants α,β and γ are themselves homogeneous in x.We actually have β(f,λx)= λβ(f,x), γ(f,λx)= λ−1γ(f,x)and α(f,λx)= α(f,x)for all λ /=0.This property motivates the following projective version for them:

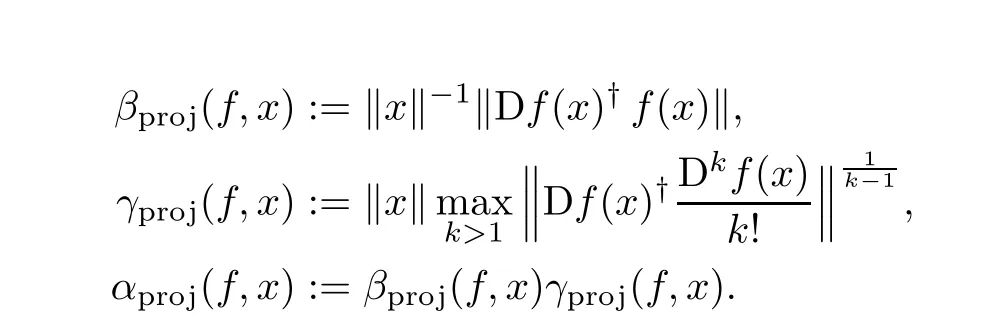
These projective versions coincide with the previous expressions when x ∈ Snand an α-Theorem for them is easily derived from Theorem 2.2 below.Furthermore,βprojstill measures the(scaled)length of the Newton step,and γprojrelates to the condition number via the following bound(known as the Higher Derivative Estimate),

The proof of this bound is the one of[8,Theorem 2,p.267]which still holds for m≤n and Df(x)†instead of Df(x)

The right-hand side in inequality(2.2)is easily computable.We canfind similar computable versions for α and β.Indeed,for x ∈ Snwe define

Inequality(2.2)says that γ(f,x)≤ γ(f,x).We also observe that β(f,x)≤ β(f,x)since

We finally conclude that α(f,x)≤ α(f,x).

The main theorem in the theory of point estimates,see[22]and[13,Theorem 19.9]for a proof.

Theorem 2.2Letf:Rn+1→ Rm,m ≤ n+1,be analytic.Setα0=0.125.Letx∈ Rn+1withα(f,x) ＜ α0.Thenxis an approximate zero offand‖x − ξ‖ ＜ 2β(f,x)whereξis the associated zero ofx.Furthermore,ifn+1=mandα(f,x) ≤ 0.02,then all points in the ball inSnwith centerxand radius2β(f,x)are approximate zeros offwith the same associated zero.

2.6 Grids

Our algorithms work on a grid Gηon Sn,which we construct by projecting onto Sna grid on the cube.Let Cn={y ∈ Rn+1|‖y‖∞=1}and φ :Cn→ Sngiven by φ(y)

Given η:=2−kfor some k ≥ 1,we consider the uniform grid Uηof mesh η on Cn.This is the set of points in Cnwhose coordinates are of the form i2−kfor i∈ {−2k,−2k+1,···,2k}with at least one coordinate equal to 1 or−1.We denote by Gηits image by φ in Sn.An argument in elementary geometry shows that for y1,y2∈Cn,

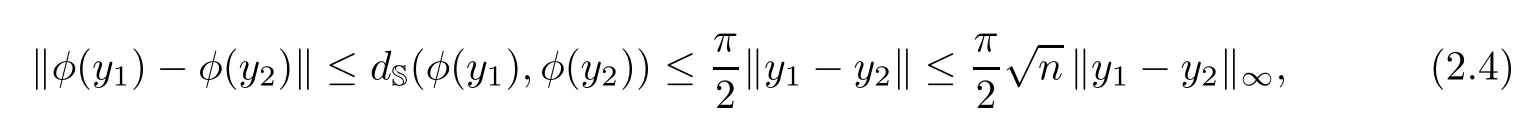
where dS(x1,x2):=arccos(〈x1,x2〉) ∈ [0,π]denotes the angular distance,for x1,x2∈ Sn.

Given ε＞ 0 and x ∈ Sn,we denote by B(x,ε):={y ∈ Rn+1|‖y − x‖ ＜ ε}the open ball with respect to the Euclidean distance and by BS(x,ε)={y ∈ Sn|dS(y,x)＜ ε}the open ball with respect to the angular distance dS.We also set from now on

The following lemma is an immediate consequence of(2.4).

Lemma 2.1The unioncovers the sphereSn.

In[19,Lemma 3.1]and[13,Lemma 19.22],the following Exclusion Lemma is proved(the statement there is for n=m but the proof holds for general m).

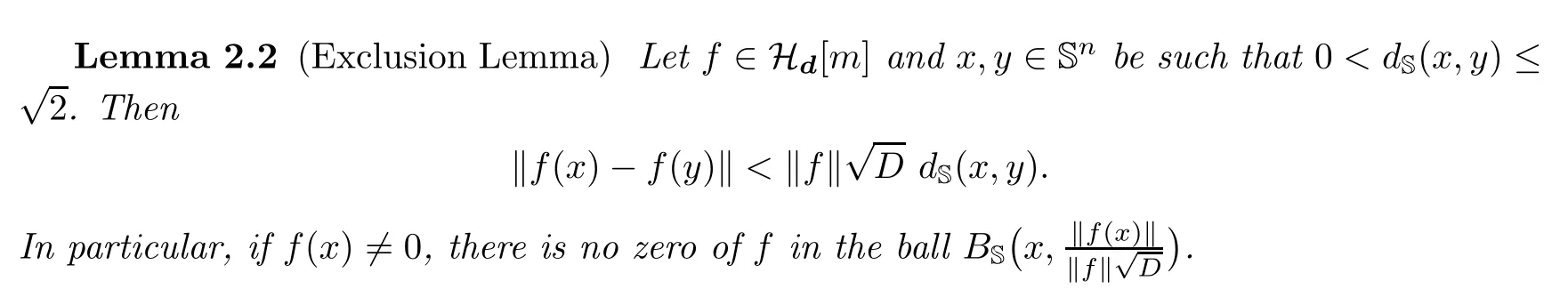
3 Solving the Problems

3.1 Feasibility

Thefirst problem we consider is the feasibility problem for systems of homogeneous polynomials.This problem was tackled in[23]and our succinct exposition closely follows[13,§19.6].We want to algorithmically solve the following problem:

Given a system f∈Hd[m],does there exist x∈Snsuch that f(x)=0?

To analyze our algorithm we will need a notion of condition for the input system.Let ZS(f)denote the set of zeros of f on the unit sphere Sn.For f ∈ Hd[m]we define

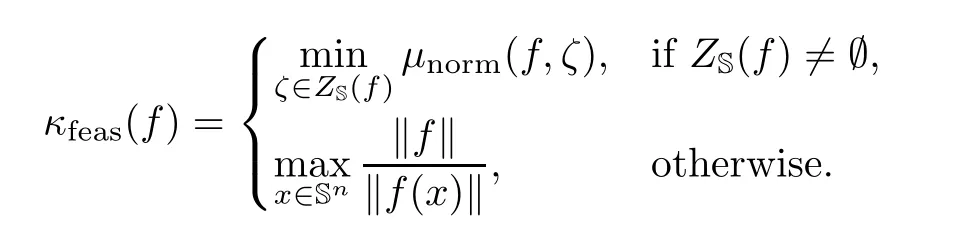
We call f well-posed when κfeas(f) ＜ ∞.Note that κfeas(f)= ∞ if and only if f is feasible and all its zeros are multiple.

The following is a pseudocode for our algorithm solving the feasibility problem.

Theorem 3.1Algorithm Feasibility works correctly:With input a well-posed system it returns“feasible”(resp.“infeasible”)if and only if the system is so.The number of iterations is bounded byO(log2(Dnκfeas(f)))and the total complexity,i.e.,the number of arithmetic operations performed by the algorithm,by(nDκfeas(f))O(n).

ProofThe correctness in the feasible case is a trivial consequence of Theorem 2.2 and the inequality α(f,x) ≤ α(f,x).The correctness in the infeasible case follows from Lemma 2.2 along with the inequalities(2.4).

To see the complexity bound,assume first that f is feasible and let ζ in the cube Cn,ζ∈ Z(f),be such that κfeas(f)= µnorm(f,ζ).Let k be such that

Here C and ε are the constants in Proposition 2.1.Let x ∈ Uηbe such that ‖x − ζ‖∞≤ η.Then,by(2.4),

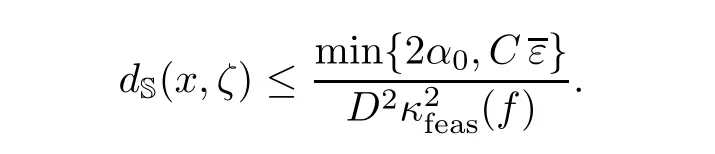
Proposition 2.1 applies,and we have

Also,by Lemma 2.2,

We then have

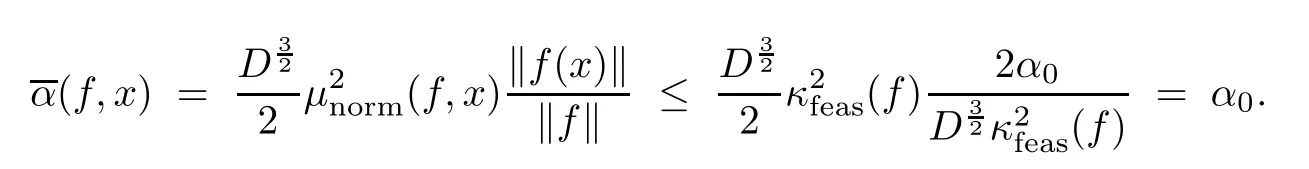
It follows that algorithm Feasibility halts at this point,and therefore the number k of iterations performed is at most O(log2(Dnκfeas(f))).

Assumefinally that f is infeasible and let k be such that

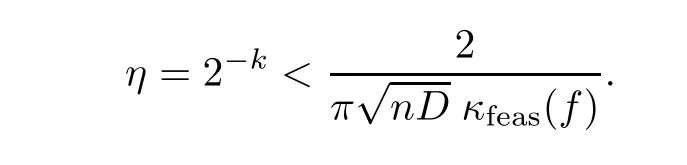
Then,at any point y∈Uηwe have

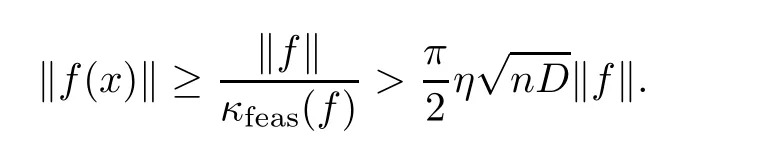
Again,algorithm Feasibility halts for this value of η,and the number k of iterations performed is also bounded by O(log2(Dnκfeas(f))).

At each iteration there are 2(n+1)?）npoints in the grid.Hence,the number of points in the finest grid(the last run of the iteration)isx we evaluate µnorm(f,x)and ‖f(x)‖,both with cost O(N).The total complexity is therefore bounded by

where we used that N≤m(n+D)n.

Remark 3.1Afinite-precision version of algorithm Feasibility can be implemented as well following the template result in Subsection 2.4(see[23]for details).The running time remains of the same order and the returned tag is correct.Thefinest precision required by the algorithm satisfies

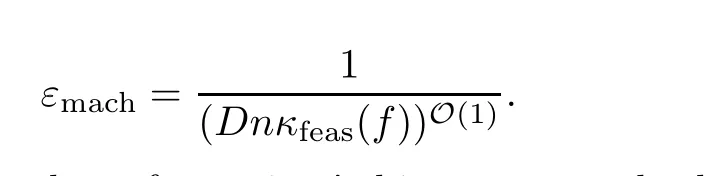
This shows that the required number of mantissa’s bits to correctly decide feasibility is logarithmic in D,n and the condition κfeas(f).The reason behind this reasonable bounds for an exponential time algorithm is that the algorithm performs an exponentially large of independent computations,each of them requiring only polynomial time and having a very simple nature.

3.2 Counting

The second problem we consider is the counting problem for square systems of homogeneous polynomials.That is,we consider systems in Hd:=Hd[n]with n polynomials in n+1 homogeneous variables.The zero set of one such system f is a finite set of,say ℓ,lines passing through the origin in Rn+1.We can see this set as the set of zeros of f in projective space P(Rn+1)and we note that this set arises from the identification of antipodal points of the zero set ZS(f),which consists of 2ℓ points.We thus want to algorithmically solve the following problem.

Given a system f∈Hd,count the number of points x∈P(Rn+1)such that f(x)=0?

This problem was studied in[19—21]and,again,our exposition closely follows[13,§19.4].As with the feasibility problem,our first step is to define an appropriate condition number.To do so now for a system f it is not enough to just consider the condition at its zeros.For points x∈ Rn+1where‖f(x)‖is non-zero but small,small perturbations of f can turn x into a new zero(and thus change its number of zeros).The following definition goes back to[17]:

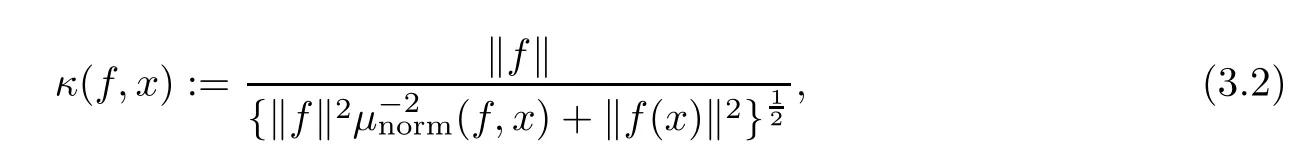
where µnorm(f,x)is defined as in(2.1)for x ∈ Sn,with the convention that∞−1=0 and 0−1= ∞,and

We observe that,because of Remark 2.1,κ(λf)= κ(f).We also note that κ(f)= ∞ if and only if there exists ξ∈ Snsuch that f(ξ)=0(i.e.,ξ∈ MS)and Df(ξ)is not surjective,i.e.,f belongs to the set

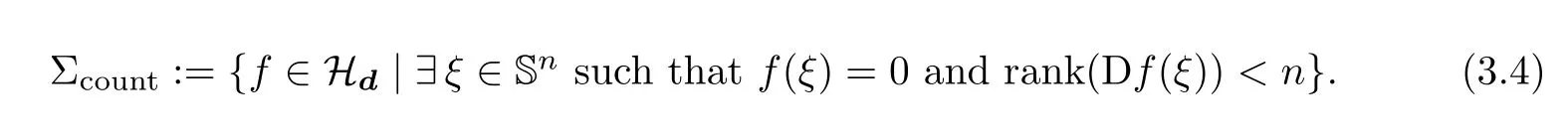
The following result(see[20]or[13,Theorem 19.3])relates condition to the distance to illposedness.It is a version,for polynomial systems,of the classical Eckard-Young theorem(see[26]).

Proposition 3.1For allf∈Hd,

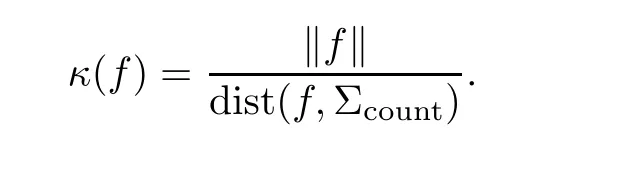
Our algorithm to solve the counting problem(described below)relies on some graph theoretical ideas.We consider,as in the previous section,a number η ∈ (0,1)and the grid Gη.We associate to this grid the graph Gηdefined as follows.We set

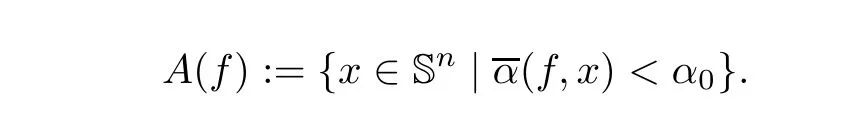
The vertices of the graph are the points in Gη∩A(f).Two vertices x,y∈Gηare joined by an edge if and only if

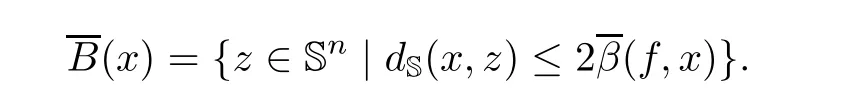
Note that as a simple consequence of Theorem 2.2,we obtain the following lemma.

The following lemma implies that the connected components of the graph Gηare of a very special nature:they are cliques.It also implies that

Lemma 3.2(a)For each componentUofGη,there is a unique zeroζU∈ ZS(f)such thatζU∈W(U).Moreover,

(b)IfUandVare different components ofGη,thenζU/= ζV.

Proof(a)Let x ∈ U.Since x ∈ A(f),by Lemma 3.1(a)there exists a zero ζxof f in(x)⊆W(U).This shows the existence.For the uniqueness and the second assertion,assume that there exist zeros ζ and ξ of f in W(U).Let x,y ∈ U be such that ζ∈Since U is connected,there exist x0=x,x1,···,xk−1,xk:=y in A(f)such that(xi,xi+1)is an edge of Gηfor i=0,···,k − 1,that is,zeros of xiand xi+1in ZS(f)respectively,then by Lemma 3.1(b)we have ζi= ζi+1,and thus

(b)Let ζU∈and x and y are joined by an edge;hence U=V.

If equality holds in(3.5),we can compute|ZS(f)|by computing the number of connected components of Gη.The reverse inequality in(3.5)amounts to the fact that there are no zeros of f in Snthat are not in W(Gη).To verify that this is the case,we want to find,for each point x∈GnA(f),a ball centered at x such that f/=0 on this ball.In addition,we want the union of these balls to cover SnW(Gη).

These considerations lead to the following algorithm:

Theorem 3.2Given an inputf∈HdΣcount,Algorithm Zero Counting:

(a)Returns the number of zeros offinP(Rn+1).

(b)PerformsO(log2(nDκ(f)))iterations and has a total cost(number of arithmetic operations)satisfying

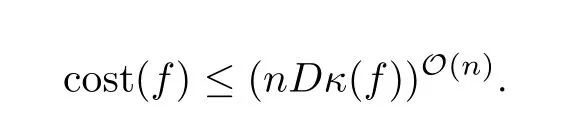
(c)It can be modified to return,in addition,at the same cost,and for each real zeroζ∈P(Rn+1)off,an approximate zeroxoffwith associated zeroζ.

(d)AssumeHdis endowed with the standard Gaussian.Then,with probability at least1−(nD)−nwe havecost(f)≤ (nD)O(n2).

(e)Similarly,with probability at least1−2−Nwe havecost(f)≤ 2O(N32).

Sketch of Proof(a)This part claims the correctness of algorithm Zero Counting.To prove it,we use some notions of spherical convexity.

Let Hnbe an open hemisphere in Snand x1,···,xq∈ Hn.Recall that the spherical convex hull of{x1,···,xq}is defined by

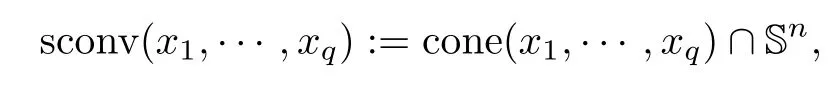
where cone(x1,···,xq)is the smallest convex cone with vertex at the origin and containing the points x1,···,xq.

Lemma 3.3Letx1,···,xq∈ Hn⊂ Rn+1

ProofLet x ∈ sconv(x1,···,xq)and yWe will prove that x∈BS(xi,ri)for some i.Without loss of generality we assume x/=y.Let H be the open half-space

We have

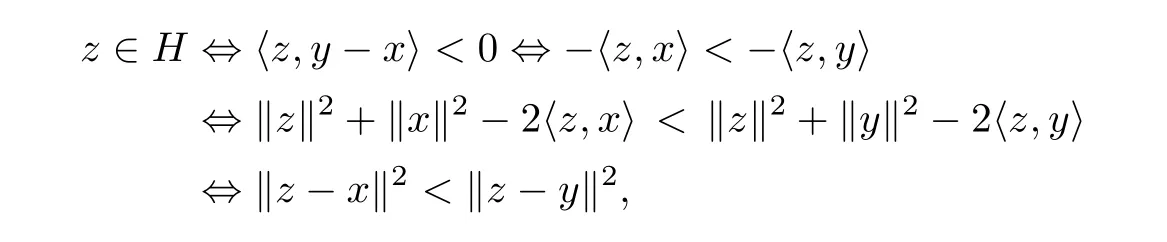
the second line following from ‖x‖= ‖y‖=1.Therefore the half-space H is the set of points z in Rn+1such that the Euclidean distance‖z−x‖ is less than ‖z−y‖.

On the other hand,H must contain at least one point of the set{x1,···,xq},since if this were not the case,the convex set cone(x1,···,xq)would be contained in{z:〈z,y − x〉≥ 0},contradicting x ∈ sconv(x1,···,xq).Therefore,there exists i such that xi∈ H.It follows that

Since the function z → 2arcsin?）giving the length of an arc as a function of its chord is nondecreasing,we obtain

We can now proceed.Assume that Algorithm Zero Countinghalts.We want to show that if r equals the number of connected components of Gη,then#R(f)=#ZS(f)/2=.We already know by Lemma 3.2 that each connected component U of Gηdetermines uniquely a zero ζU∈ ZS(f).Thus it is enough to prove that ZS(f)⊆ W(Gη).This would prove the reverse inequality in(3.5).

Assume,by way of contradiction,that there is a zero ζ of f in Snsuch that ζ is not in W(Gη).Let B∞(φ−1(ζ),η):={y ∈ Uη|‖y − φ−1(ζ)‖∞≤ η}={y1,···,yq},the set of all neighbors of φ−1(ζ)in Uη,and let xi= φ(yi),i=1,···,q.Clearly, φ−1(ζ)is in the cone spanned by{y1,···,yq},and hence ζ∈ sconv(x1,···,xq).

We claim that there exists j ≤ q such that xj/∈ A(f).Indeed,assume that this is not the case.We consider two cases.

(i)All the xibelong to the same connected component U of Gη.In this case Lemma 3.2 ensures that there exists a unique zero ζU∈ Snof f in W(U)andx1,···,xqlie in an open half-space of Rn+1,we may apply Lemma 3.3 to deduce that

It follows that for some i∈ {1,···,q},ζ∈⊆ W,contradicting that ζ/∈ W(Gη).

(ii)There exist ℓ/=s and 1≤ j＜ k≤ rthat xℓ∈ Ujand xs∈ Uk.Since condition(a)in the algorithm is satisfied,But by the bounds(2.4),

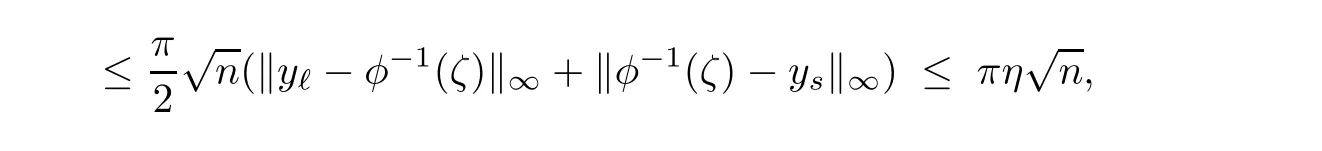
a contradiction.

We have thus proved the claim.Let then 1≤j≤q be such that xj/∈A(f).Then,using Lemma 2.2,

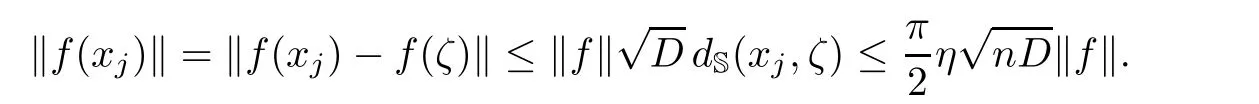
This is in contradiction with condition(b)in the algorithm being satisfied.

(b)We next prove the claimed bound for the cost.The idea is to show that when η becomes small enough,as a function of κ(f),n,N and D,then conditions(a)and(b)in algorithm Zero Counting are satisfied.To do so,we rely on the following result(see[13,Lemma 19.26]).

Lemma 3.4Letx1,x2∈ Gηwith associated zerosζ1/= ζ2.If

which implies

We can now conclude the proof of part(b).Assume

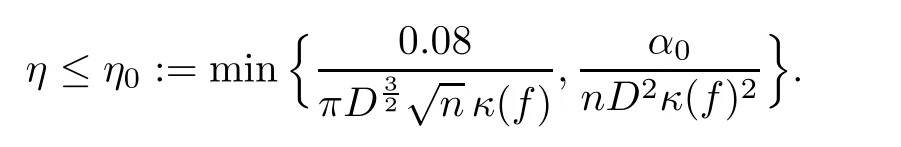
Then the hypotheses of Lemmas 3.4—3.5 hold.The first of these lemmas ensures that condition(a)in algorithm Zero Counting is satisfied,the second,that condition(b)is satisfied as well.Therefore,the algorithm halts as soon as η ≤ η0.This gives a bound of O(log2(nDκ(f)))for the number of iterations.

At each iteration there are K:=2(n+1)points in the grid.For each such point x we evaluate µnorm(f,x)and ‖f(x)‖,both with cost O(N).We can therefore decide with cost O(KN)which of these points are vertices of Gηand for those points x compute the radiusTherefore,with cost O(K2N)we can compute the edges of Gη.The number of connected components of Gηis then computed with O(K2N)operations as well by standard algorithms in graph theory(see the Notes for references).

Since dSis computed with O(n)operations,the total cost of verifying condition(a)is at most O(),and the additional cost of verifying(b)is O(K).It follows that the cost of each iteration is O(K2N).Furthermore,since at these iterations η≥ η0,we have K ≤ (C(n+1)D2κ(f)2)n+1.Using this estimate in the O(K2N)cost of each iteration and multiplying by the bound O(log2(nDκ(f)))for the number of iterations,the claimed bound for the total cost follows.

(c)To prove this part just note that for i=1,···,r,any vertex xiof Uiis an approximate zero of the only zero of f in W(Ui).

(d)The probabilistic analysis relies,among other results,on understanding the nature of a particular complex algebraic set.For q≤n+1 let

Hence,using part(b),for c large enough,we have

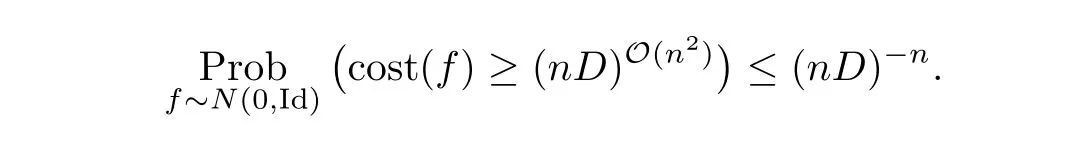
(e)We now take t=2cNwith a constant c large enough and use that N≥(as we may assume that there is at least one polynomial of degree 2).

Remark 3.2As with algorithm Feasibility,afinite-precision version of algorithm Zero Counting,has been analyzed in[19].Again,the running time remains of the same order and the returned value is the number of zeros of the input f in P(Rn+1)as long as the round-offunit satisfies

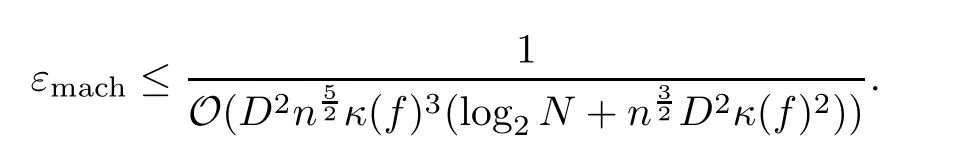
We note now that the probability tail for κ(f)implies that,with probability at least 1 −(nD)−nthe number of mantissa’s bits necessary to ensure correctness of the computed result is O(log(nD)).

3.3 Homology

The last problem we consider is the computation of the homology of basic semialgebraic sets.These are subsets of Rndefined by a system of equalities and inequalities

where F=(f1,···,fq)and G=(g1,···,gs)are tuples of polynomials with real coefficients and the expression g(x)≻0 stands for either g(x)≥0 or g(x)＞0(we use this notation to emphasize the fact that our main result does not depend on whether the inequalities in(3.6)are strict).Let W(F,G)denote the solution set of the semialgebraic system(3.6),for a vector d=(d1,···,dq+s)of q+s positive integers,let Pd(or Pd[q;s]to emphasize the number of components)denote the linear space of the(q+s)-tuples of real polynomials in n variables of degree d1,···,dq+s,respectively.Our(clearly more ambitious)goal now is the following:

Given(F,G)∈Pd[q;s],compute the homology groups of W(F,G).

A numerical algorithm solving this problem was recently given in[14].Our exposition follows this paper.

Afirst remark is that the set W(F,G)may be unbounded and hence,not suitable for our grid methods.The obvious solution is to “fit it” into a sphere via homogeneization.Given a degree pattern d=(d1,···,dq+s),the homogeneization of polynomials(with respect to that pattern)yields an isomorphism of linear spaces

where Fhdenotes the homogeneization of F with homogeneizing variable X0.The Weyl inner product on Hd[q;s]induces an inner product on Pd[q;s]such that the above map is isometric.The set W(F,G) ⊆ Rnis diffeomorphic to the subset of Sndefined by Fhm=0,Ghm≻ 0 and X0＞0 and we can therefore focus on computing the homology of the latter.As it happens,we can further relax the inequalities in this system.But to justify this we need to understand condition.

A(closed)homogeneous semialgebraic system has the form

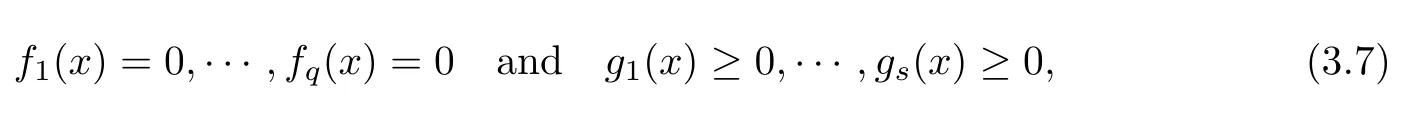
where fiand gjare homogeneous polynomials in R[X0,X1,···,Xn].The system is therefore an element(F,G)∈Hd[q;s].The set of solutions x∈Snof system(3.7),which we will denote by S(F,G),is a spherical basic semialgebraic set.To such a system(F,G)we associate the condition number κ∗(F,G)as follows.For a subtuple L=(gj1,···,gjℓ)of G,we denote by FLthe system obtained from F by appending the polynomials from L,that is,

where now d denotes the appropriate degree pattern in Nq+ℓ.Abusing notation,we will frequently use set notations L⊆G or g∈G to denote subtuples or coefficients of G.

Definition 3.1Letq≤ n+1,(F,G)∈ Hd[q;s].The condition number of the homogeneous semialgebraic system(F,G)is defined as

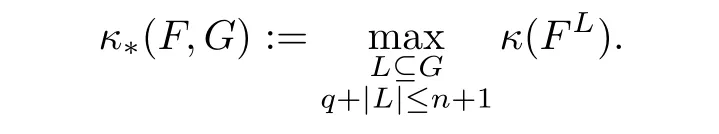
We defineΣ∗as the set of all(F,G)∈ Hd[q;s]such thatκ∗(F,G)= ∞.

Clearly,Σ∗is semialgebraic and invariant under scaling of the q+s components.

The next result,Proposition 4.14 in[14],shows that we can relax inequalities.

Proposition 3.3Let(F,G) ∈ Hd[q;s]be such thatκ∗(F,G) ＜ ∞.PutS:=S(F,G),letr≤ s,and letS′⊆ Sbe the solution set inSnof the semialgebraic system

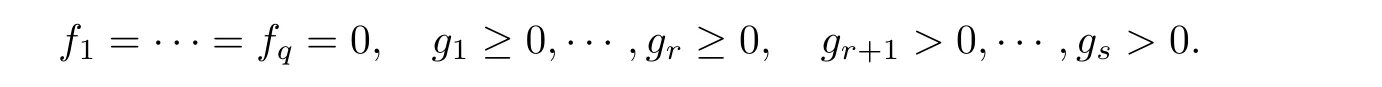
Moreover,let∂Sdenote the boundary ofSinS(F,∅).ThenS∂S ⊆ S′andS′is homotopically equivalent toS.

We have thus reduced our problem to the computation of the homology of the set S(H(F,G))where H(F,G)denotes the homogeneous semialgebraic system

Note the coefficient‖(F,G)‖in the last polynomial.This coefficient does not change the solution set in Snbut allows us to control the condition(by avoiding artificial differences in the scaling of the polynomials of H(F,G)).Indeed,for ψ =(F,G) ∈ Pd[q;s],we define

3.3.1 The reach of a closed set

Let E be a real Euclidean space offinite dimension.For a nonempty subset W ⊆ E and x∈E,we denote by dW(x):=the distance of x to W.

Definition 3.2LetW ⊆ Ebe a nonempty closed subset.The medial axis ofWis defined as the closure of the set

The reach(or local feature size)ofWat a pointp ∈ Wis defined asτ(W,p):=dΔW(p).The(global)reach ofWis defined asτ(W):We also setτ(∅):=+∞.

By the(open)neighborhood of radius r≥0 around a nonempty set S⊆E we understand the set

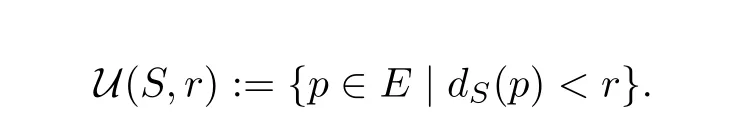
In[33,Proposition 7.1],Niyogi,Smale and Weinberger gave an answer to the following question:Given a compact submanifold S ⊆ E,afinite set X ⊂ E and ε＞ 0,which conditions do we need to ensure that S is a deformation retract of U(X,ε)?

Theorem 3.3 below(see[14,§2.2]for a proof)gives an extension to their result to any compact subsets S,X provided S has positive reach τ(S).

Recall that the Hausdorff distance between two nonempty closed subsets A,B ⊆ E is defined as

Theorem 3.3LetSandXbe nonempty compact subsets ofE.The setSis a deformation retract ofU(X,∈)for any∈such that3dH(S,X)＜ ∈＜τ(S).

Theorem 3.3 is the main stepping stone towards computing the homology groups of S(H(F,G)).The reach τ(S(H(F,G)))of this set,however,is not easily computable.The following result,Theorem 4.12 in[14],shows a simple bound for it in terms of κ∗.

Theorem 3.4For any homogeneous semialgebraic system(F,G)defining a semialgebraic setS:=S(F,G)⊆ Sn,ifκ∗(F,G)＜ ∞,then

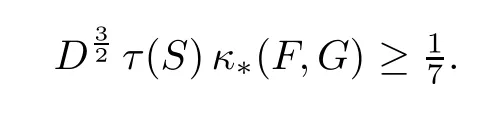
3.3.2 Tubes and relaxations

For a subset A⊆Snwe denote by

the open r-neighborhood of A with respect to the geodesic distance dSon the sphere Sn.Also,for a homogeneous system(F,G)∈ Hd[q;s]and r＞ 0,we define the r-relaxation of S(F,G):

It is clear that S(F,G)⊆Approx(F,G,r)for any r＞0.Also,it is easy to see that Approx(F,G,r)converges to S with respect to the Hausdorff distance,when r→ 0.The next two results(see[14,§4.2])quantify more precisely this behaviour in terms of the condition number κ∗(F,G).Recall that D denotes the maximum degree of the components of F and G.

Proposition 3.5For anyr＞0,

Theorem 3.5Letq ≤ n+1.For any positive numberr ＜

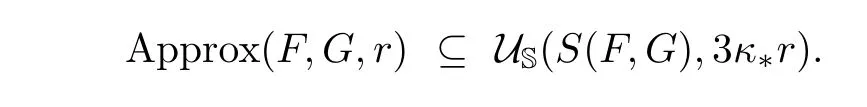
3.3.3 Algorithms and analyses

We can now describe an algorithm computing a covering for S(F,G),with(F,G)∈Hd[q;s],as in Theorem 3.3.

Proposition 3.6On inputFandG,algorithm covering outputs afinite setXand anε＞ 0such thatU(X,ε)is homotopically equivalent toS(F,G).Moreover,the computation performs((s+n)Dκ∗)O(n)arithmetic operations,wheres=|G|andκ∗= κ∗(F,G),and the number|X|of points inXis(nDκ∗)O(n).

ProofLet κ∗:= κ∗(F,G),S:=S(F,G)and let η,r,and K∗be the values of the corresponding variables after the repeat loop terminates in algorithm covering.By design,

We willfirst show that

Let L ⊆ G and y ∈ Snbe such that κ∗= κ(FL)= κ(FL,y).Because of Lemma 2.1 there is some x ∈ Gηsuch that dS(x,y)＜ r,and κ(FL,x)≤ K∗by the definition of K∗.Since the map

the last as D≥2 and K∗≥1,and Inequality(3.9)follows.Let X:=Gη∩ Approx(F,G,D12r)and ∈:=5DK∗r,that is,thefinite set and the real number output by the algorithm.We will now prove that U(X,∈)is homotopically equivalent to S.By Theorem 3.3,it is enough to prove the inequalities

The second inequality follows from Inequalities(3.8)—(3.9)and Theorem 3.4:

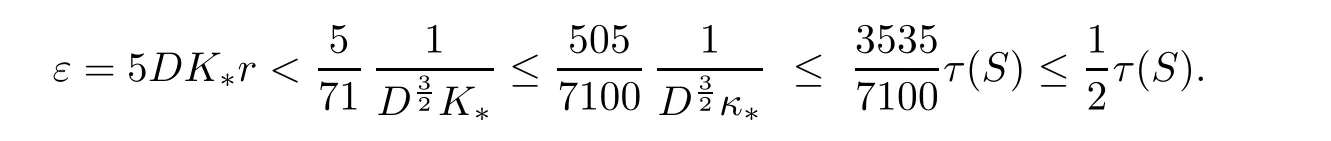
Concerning the inequality 3dH(X,S)＜ ∈,let x∈ S.Because of Lemma 2.1,there is some y∈Gηwith dS(x,y)＜r.Hence y lies in Approx(F,G,D12r),by Proposition 3.5.Thus y∈X and d(x,X)＜dS(x,y)＜r＜ε.

Next,let x∈X.Then,x∈Approx(F,G,r)and

the last by Inequality(3.8).Hence,Theorem 3.5 applies and shows that

where we used D ≥ 2 for the last inequality.Thus we have shown that dH(X,S)＜∈.This concludes the proof of(3.10)and of the homotopy equivalence.

Lastly,we deal with the complexity analysis.We can approximate κ(FL,x)within a factor of 2 in O(N+n3)operations(see[31,§2.5])and this is enough for our needs.For simplicity,we will do as if we could compute κ exactly.

the last because S is a deformation retract of U(X,ε).The process is described in detail in[22,§4]where the proof for the following result can be found.

Proposition 3.7Given afinite setX ⊆ Rn+1and a positive real number∈,one cancompute the homologywith|X|O(n)operations.

Wefinally can put all the ingredients together in our main result.

Theorem 3.6There is an algorithm Homology,working over the reals and numerically stable that,given a system(F,G)∈Pdwithq≤nequalities andsinequalities,computes the homology groups ofW(F,G).Moreover,the number of arithmetic operations inRperformed by Homology on input(F,G),denotedcost(F,G),satisfies

(a)cost(F,G)=((s+n)Dδ−1)O(n2)whereδis the distance of

Furthermore,if(F,G)is drawn from the Gaussian measure onPd,then

(b)cost(F,G)≤ ((s+n)D)O(n3)with probability at least1−((s+n)D)−n,

(c)cost(F,G)≤ 2O(N2)with probability at least1−2−N.

Sketch of ProofFollowing our previous stream of thoughts we consider the following algorithm:

Remark 3.3(i)As with algorithms Feasibility and Zero Counting,afinite-precision version of Homology can be implemented.This has not been done but would follow the same steps as in the other two cases and ensure that the computed homology groups(i.e.,the Betti numbers and torsion coefficients corresponding to these groups)are correct as long as

A discussion of this theme is in[22,§7].

(ii)It is immediate to check that κfeas(f)≤ κ∗(f).Hence,the probabilistic analysis for the latter gives bounds for the former as well.But the fact that the codimension of Σfeas:={f|κfeas(f)= ∞}is much greater than that of Σcount(which is equal to one)suggests that one might obtain substantially better bounds.There are no results as of today,however,supporting this suggestion.

[1]Allgower,E.L.and Georg,K.,Numerical Continuation Methods,Springer-Verlag,Berlin,1990.

[2]Amelunxen,D.and Lotz,M.,Average-case complexity without the black swans,J.Complexity,41,2017,82–101.

[3]Basu,S.,Algorithmic semi-algebraic geometry and topology—recent progress and open problems,Surveys on discrete and computational geometry,Contemp.Math.,453,Amer.Math.Soc.,Providence,RI,2008,139–212.

[4]Basu,S.,Pollack,R.and Roy,M.-F.,On the combinatorial and algebraic complexity of quantifier elimination,35th Annual IEEE Symp.on Foundations of Computer Science,1994,632–641.

[5]Basu,S.,Pollack,R.and Roy,M.-F.,Algorithms in Real Algebraic Geometry,2nd ed.,Algorithms and Computation in Mathematics,10,Springer-Verlag,Berlin,2006.

[6]Benedetti,R.and Risler,J.-J.,Real algebraic and semi-algebraic sets,Hermann,Paris,1990.

[7]Bjö rner,A.,Topological methods,Handbook of Combinatorics,R.Graham,M.Grotschel and L.Lovasz(eds.),North-Holland,Amsterdam,1995,1819–1872.

[8]Blum,L.,Cucker,F.,Shub,M.and Smale,S.,Complexity and Real Computation,Springer-Verlag,New York,1998.

[9]Blum,L.,Shub,M.and Smale,S.,On a theory of computation and complexity over the real numbers:NP-completeness,recursive functions and universal machines,Bulletin of the Amer.Math.Soc.,21,1989,1–46.

[10]Bochnak,J.,Coste,M.and Roy,M.-F.,Real Algebraic Geometry,Ergebnisse der Mathematik und Ihrer Grenzgebiete(3),36,Springer-Verlag,Berlin,1998.

[11]Bürgisser,P.and Cucker,F.,Counting complexity classes for numeric computations II:Algebraic and semialgebraic sets,J.Complexity,22,2006,147–191.

[12]Bürgisser,P.and Cucker,F.,Exotic quantifiers,complexity classes,and complete problems,Found.Comput.Math.,9,2009,135–170.

[13]Bürgisser,P.and Cucker,F.,Condition,Grundlehren der Mathematischen Wissenschaften,349,Springer-Verlag,Berlin,2013.

[14]Bürgisser,P.,Cucker,F.and Lairez,P.,Computing the homology of basic semialgebraic sets in weakly exponential time,2017,arXiv:1706.07473.

[15]Carlson,J.,Jaffe,A.,Wiles,A.,et al.,The Millenium Prize Problems,Clay Mathematics Institute,Cambridge,MA,American Mathematical Society,Providence,RI,2006.

[16]Collins,G.E.,Quantifier elimination for real closed fields by cylindrical algebraic deccomposition,Lect.Notes in Comp.Sci.,33,Springer-Verlag,Berlin,1975,134–183.

[17]Cucker,F.,Approximate zeros and condition numbers,J.Complexity,15,1999,214–226.

[18]Cucker,F.,A theory of complexity,condition and roundoff,Forum of Mathematics,Sigma,e4,2015.

[19]Cucker,F.,Krick,T.,Malajovich,G.and Wschebor,M.,A numerical algorithm for zero counting,I:Complexity and accuracy,J.Complexity,24,2008,582–605.

[20]Cucker,F.,Krick,T.,Malajovich,G.and Wschebor,M.,A numerical algorithm for zero counting,II:Distance to ill-posedness and smoothed analysis,J.Fixed Point Theory Appl.,6,2009,285–294.

[21]Cucker,F.,Krick,T.,Malajovich,G.and Wschebor,M.,A numerical algorithm for zero counting,III:Randomization and condition,Adv.Applied Math.,48,2012,215–248.

[22]Cucker,F.,Krick,T.and Shub,M.,Computing the homology of real projective sets,Found.Comp.Math.,2016,arXiv:1602.02094.

[23]Cucker,F.and Smale,S.,Complexity estimates depending on condition and round-offerror,Journal of the ACM,46,1999,113–184.

[24]Demmel,J.,On condition numbers and the distance to the nearest ill-posed problem,Numer.Math.,51,1987,251–289.

[25]Demmel,J.W.,Applied Numerical Linear Algebra,SIAM,Philadelphia,1997.

[26]Eckart,C.and Young,G.,The approximation of one matrix by another of lower rank,Psychometrika,1,1936,211–218.

[27]Grigoriev,D.Yu.,Complexity of deciding Tarski algebra,Journal of Symbolic Computation,5,1988,65–108.

[28]Grigoriev,D.Yu.and Vorobjov,N.N.,Solving systems of polynomial inequalities in subexponential time,Journal of Symbolic Computation,5,1988,37–64.

[29]Koiran,P.,The real dimension problem is NPR-complete,Journal Complexity,15,1999,227–238.

[30]Kostlan,E.,Complexity theory of numerical linear algebra,Journal of Computational and Applied Mathematics,22,1988,219–230.

[31]Lairez,P.,A deterministic algorithm to compute approximate roots of polynomial systems in polynomial average time,Found.Comput.Math.,2017,DOI:10.1007/s10208-016-9319-7.

[32]Mehta,M.L.,Random matrices,3rd ed.,Pure and Applied Mathematics(Amsterdam),142,Elsevier/Academic Press,Amsterdam,2004.

[33]Niyogi,P.,Smale,S.and Weinberger,S.,Finding the homology of submanifolds with high confidence from random samples,Discrete Comput.Geom.,39,2008,419–441.

[34]Renegar,J.,On the computational complexity and geometry of thefirst-order theory of the reals,Part I,Journal of Symbolic Computation,13,1992,255–299.

[35]Renegar,J.,On the computational complexity and geometry of thefirst-order theory of the reals,Part II,Journal of Symbolic Computation,13,1992,301–327.

[36]Renegar,J.,On the computational complexity and geometry of thefirst-order theory of the reals,Part III,Journal of Symbolic Computation,13,1992,329–352.

[37]Renegar,J.,Incorporating condition measures into the complexity theory of linear programming,SIAM J.Optim.,5,1995,506–524.

[38]Renegar,J.,Linear programming,complexity theory and elementary functional analysis,Math.Program.,70,1995,279–351.

[39]Shub,M.and Smale,S.,Complexity of Bézout’s theorem I:Geometric aspects,Journal of the Amer.Math.Soc.,6,1993,459–501.

[40]Shub,M.and Smale,S.,Complexity of Bézout’s theorem II:Volumes and probabilities,Computational Algebraic Geometry,F.Eyssette and A.Galligo(eds.),Progress in Mathematics,109,Birkhäuser,Boston,1993,267–285.

[41]Shub,M.and Smale,S.,Complexity of Bézout’s theorem III:Condition number and packing,Journal of Complexity,9,1993,4–14.

[42]Shub,M.and Smale,S.,Complexity of Bézout’s theorem V:Polynomial time,Theoret.Comp.Sci.,133,1994,141–164.

[43]Shub,M.and Smale,S.,Complexity of Bézout’s Theorem IV:Probability of success,extensions,SIAM J.of Numer.Anal.,33,1996,128–148.

[44]Smale,S.,Newton’s method estimates from data at one point,The Merging of Disciplines:New Directions in Pure,Applied,and Computational Mathematics,R.Ewing,K.Gross and C.Martin(eds.),Springer-Verlag,New York,1986.

[45]Tarski,A.,A Decision Method for Elementary Algebra and Geometry,University of California Press,1951.

[46]Trefethen,L.N.and Bau III,D.,Numerical Linear Algebra,SIAM,Philadelphia,1997.

[47]Wüthrich,H.R.,Ein Entscheidungsverfahren für die Theorie der reell-abgeschlossenen Kö rper,Komplexität von Entscheidungsproblemen,E.Specker and V.Strassen(eds.),Lect.Notes in Comp.Sci.,43,Springer-Verlag,Berlin,1976,138–162.