Existence of Nonnegative Solutions for a Class of Systems Involving Fractional(p,q)-Laplacian Operators∗

Yongqiang FUHouwang LIPatrizia PUCCI

(Dedicated to Professor Philippe G.Ciarlet on the occasion of his 80th birthday,with high feelings of esteem for his notable contributions in mathematics and great affection)

1 Introduction

Recently,fractional p-Laplacian equations have been greatly studied,since they model several problems in Physics,Biology,Economics and so on.Thus,the research in thisfield has received a wide attention.Franzina and Palatucci[1]considered an eigenvalue problem associated with the fractional p-Laplacian operator(−Δ).In particular,they obtained some useful properties of thefirst eigenvalue.Later,Iannizzotto and Squassina[2]established the Weyl type estimates for the asymptotic behavior of variational eigenvalues.

A classical method to solve the existence and multiplicity of solutions for the elliptic equations is the Nehari manifold technique,which has received great attention.In[3]Brown and Zhang considered the following Dirichlet problem:

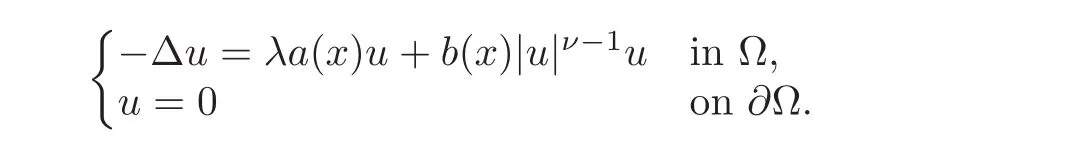
Using the Nehari manifold and the Fibering mapping,defined by

they obtained the existence and the bifurcation via the Nehari manifold method in the scalar case.

Recently,Chen and Deng[4]yielded with the following fractional p-Laplacian system:

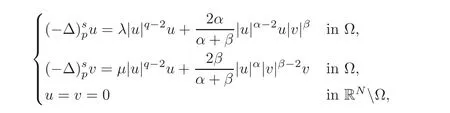
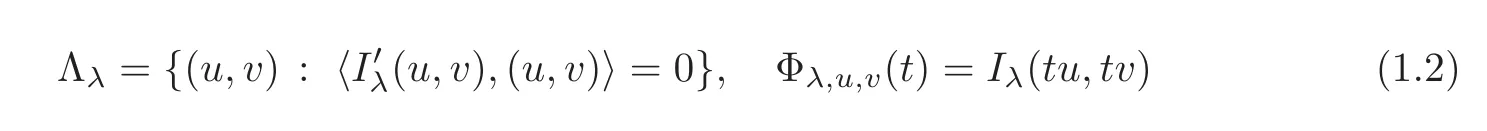
and obtained the multiplicity of the solutions.

In[5],Zhang,Liu and Liu applied the same method to the(p,q)-Laplacian system:

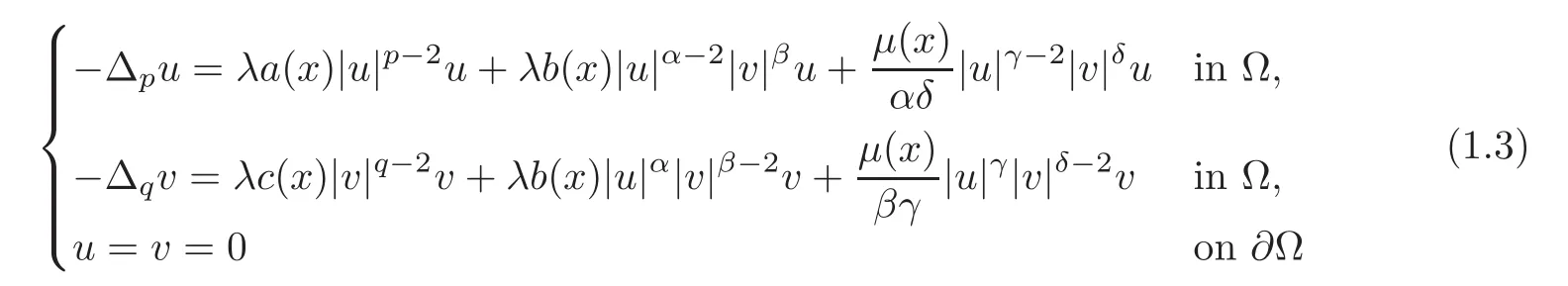
using the same definitions in(1.2).However,since in general p/=q,the definitions in(1.2)are not suitable for problem(1.3)and there are some bugs in[5].In this paper,wefix these bugs by modifying the definitions of the Nehari manifold and the Fibering mapping in(1.2),and furthermore we generalize the results to the fractional setting.

More specifically,we consider the problem

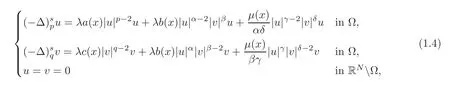
where λ ＞ 0 is a real parameter,Ω is a bounded domain in RN,with boundary∂Ω Lipschitz continuous,1＜p≤q＜∞,sq＜N,u is the fractional p-Laplacian of u,that is,

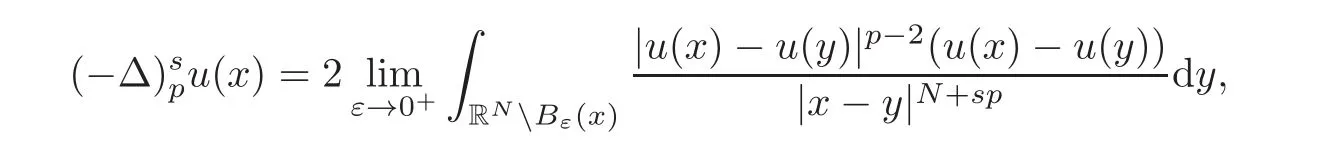
where Bε(x)is the ball of RNcentered at x and of radius ε＞ 0.Of course,the fractional q-Laplacianv of v is defined in a similar way,simply replacing p by q.Initially,we study the associated eigenvalue problem:

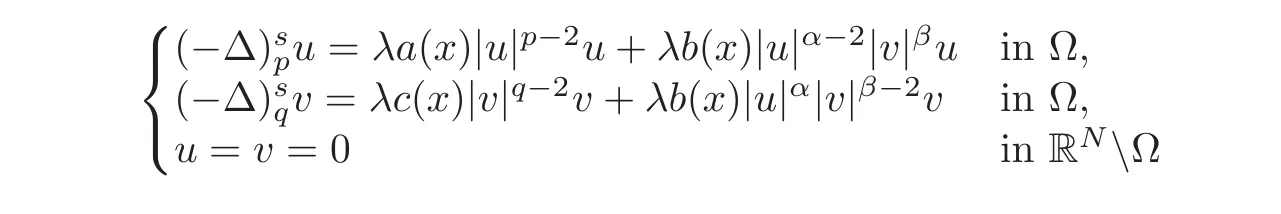
and obtain some properties of the first eigenvalue λ1of problem(1.5).

In this paper,we solve the question on the correct definitions in(1.2),since they are not suitable for the case p/=q in(1.4).We define the Nehari manifold and the Fibering mapping as

whereµis the function given in(H3),while(u1,v1)∈X is a normalized positive eigenfunction of(1.5)associated to the first eigenvalue λ1of(1.5).Then,we obtain the bifurcation property for(1.4)as λ → λ−1.Thanks to the Picone identity,we finally get a nonexistence result for(1.4)when λ ≥ λ1,provided that µ is nonnegative in Ω.

In addition to the papers already cited,the fractional(p,q)-Laplacian systems,mostly with the same p=q,have been widely studied.We refer to[5—7]and the references therein.

In the scalar case,for Dirichlet problems involving general integro-differential operator,with the structure of the fractional p-Laplacian,we cite[8],in which existence of unique weak solutions is proved by the direct method of the calculus of variations.Operators of the type treated in[8]can be used also in our context.We do not perform this extension here,and refer the interested reader to the general systems as explained in all details in Section 5 of[7].

The paper is so organized.In Section 2,we state some notations and preliminary results.In Section 3,we determine useful properties for the first eigenvalue λ1of(1.5).In Section 4,we prove the existence of solutions of(1.4)for all λ,with 0 ＜ λ ＜ λ1and the bifurcation property for(1.4)as λ →.In Section 5,we establish a nonexistence result for(1.4)when λ ≥ λ1.

2 Notations and Preliminaries

Let us introduce for clarity some classical notations,referring to[4,9]for further details.Let

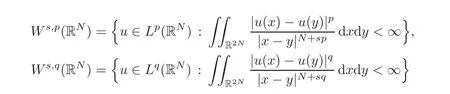
denote the standard fractional Sobolev spaces,endowed with the norms

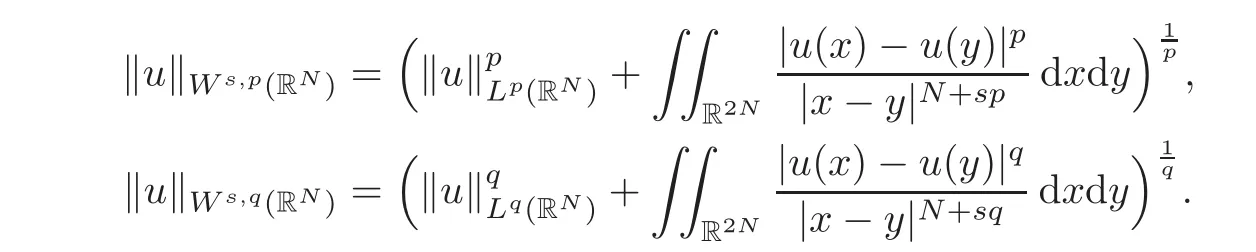
The subspaces Wp={u∈Ws,p(RN):u|RNΩ≡0},Wq={u∈Ws,q(RN):u|RNΩ≡0}of Ws,p(RN)and Ws,q(RN),respectively,are clearly closed and the norms

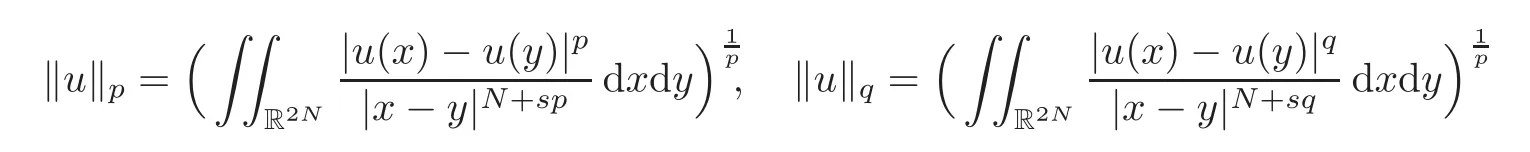
on Wpand Wq,respectively,are equivalent to ‖ ·‖Ws,p(RN)and ‖ ·‖Ws,q(RN),since ∂Ω is Lipschitz continuous(see[10,Theorem 1.4.2.2]).The solution space X=Wp×Wq,given in the Introduction,is equipped with the norm ‖(u,v)‖X= ‖u‖p+‖v‖q.For the proof of the next lemma we refer to[4,9,11].

Lemma 2.1(1)The embeddingsWqWpLν(RN)are continuous for anyν ∈ [1,]and the latter is compact,wheneverν ∈ [1,),since1 ＜ p ≤ qandsq ＜ N.

(2)X=(X,‖ ·‖X)is a real reflexive Banach space,whileWp=(Wp,‖·‖p)andWq=(Wq,‖ ·‖q)are real uniformly convex Banach spaces.

For convenience,for all(u,v) ∈ X we introduce the linear functionals Bp(u,·):Wp→ R and Bq(v,·):Wq→ R,defined by

for all φ ∈ Wpand all ψ ∈ Wq,respectively.

Thanks to the main assumptions(H1)—(H3),given in the Introduction,the next two definitions make sense.

Definition 2.1We say that(u,v)∈ Xis a(weak)solution of problem(1.4),if

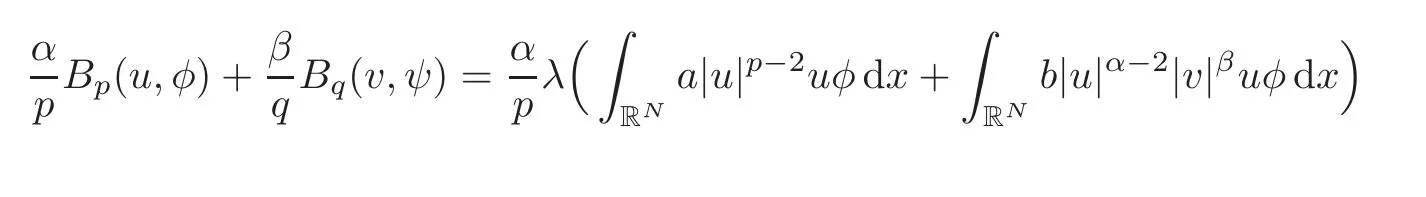
for any(φ,ψ)∈ X.

Definition 2.2We say that(u,v) ∈ Xis aneigenfunction associated to λfor problem(1.5),if

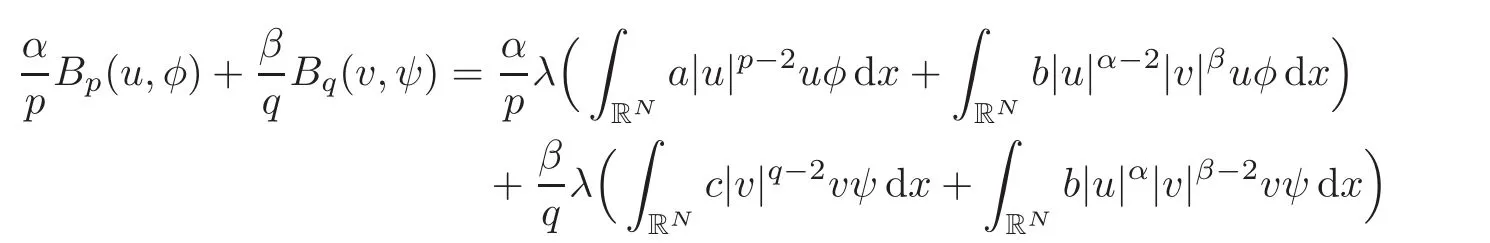
for any(φ,ψ)∈ X.

It is well known that problem(1.4)has a variational structure,i.e.,(weak)solutions of problem(1.4)are exactly the critical points of the associated functional

from X into R,where

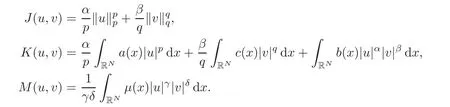
Lemma 2.2The functionalJ:X→Ris weakly lower semicontinuous inX,andK,andMare compact inX.

ProofThe weak lower semicontinuity of J in X is obtained from the weak lower semicontinuity in X of the norms‖ ·‖pand ‖ ·‖q.Indeed,if(un,vn)⇀ (u,v)in X as n → ∞,then un⇀u in Wpand vn⇀v in Wqas n→∞,so that

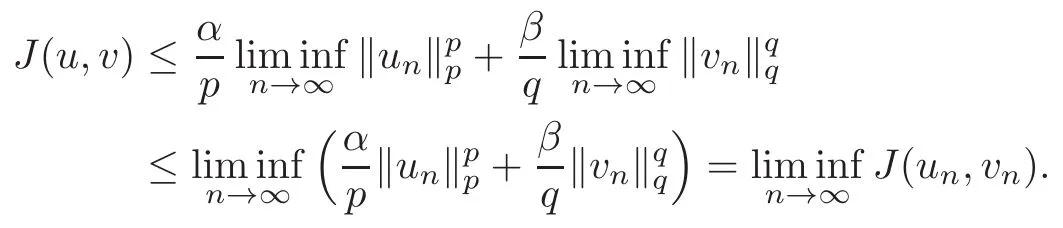
We refer to[12,Lemma 2.1]for a proof of the fact that K and M are compact in X,since the changes are obvious.

3 Some Properties of the First Eigenvalue

Assume that u≥0 and v＞0.Put

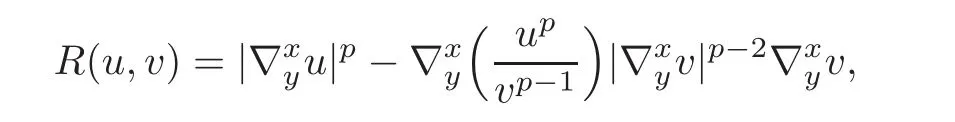
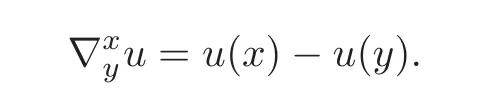
where Before getting the main result of this section,we give a lemma.

Lemma 3.1Assume thatλ ＞ 0and that(u1,v1) ∈ Xis a positive vector function inΩ,such that for any(φ,ψ)∈ X,

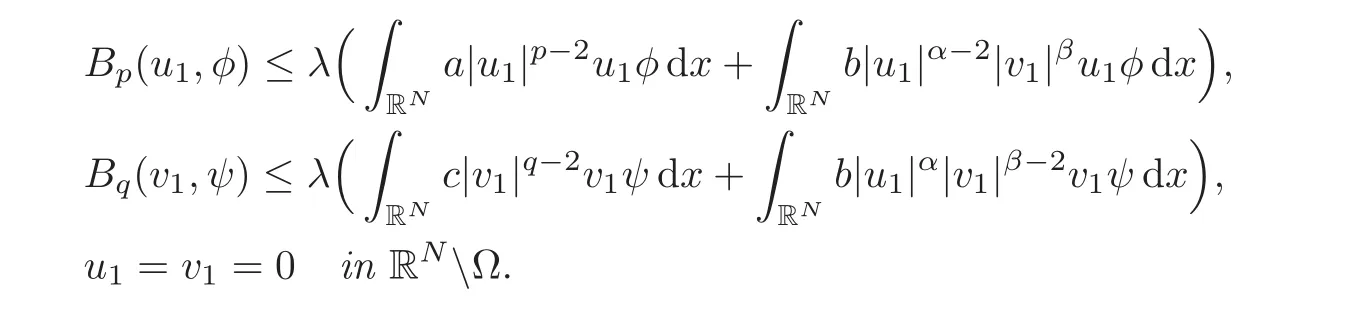
Then for any(u2,v2)∈ X,which is positive inΩand satisfies the inequalities

for any(φ,ψ)∈ X,there exists a constantC ＞ 0such that(u2,v2)=

ProofBy the Picone identity(see[13,Theorem 6.2])we get

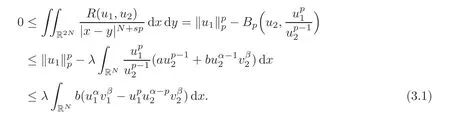
Using the same method,we have

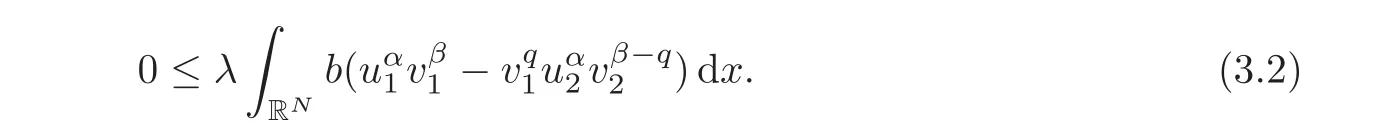
Therefore,multiplying(3.1)byand adding them,we get

by the Young inequality,since=1 by(H1).Hence the integral in(3.3)is zero and so,in particular by(3.1)—(3.2),

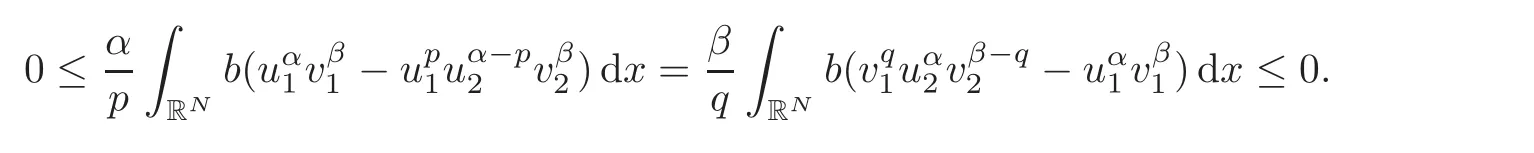
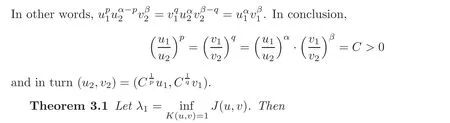
(1)λ1＞ 0;

(2)there exists(u1,v1)∈ Xwhich is the eigenfunction associated toλ1of the problem(1.5)and(u1,v1)is positive inΩ;

(3)the eigenspace associated toλ1is simple,that is,thefirst eigenspace

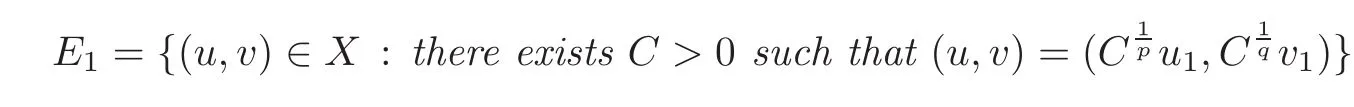
has dimension1;

(4) λ1is the only eigenvalue of problem(1.5)whose eigenfunctions are positive inΩ.

Proof(1)It is easy to see that

for all(φ,ψ)∈ X,where

4 The Case 0＜λ＜λ1

In this section,we use the Nehari manifold method to prove the existence and bifurcation of the solutions for problem(1.4).First,put

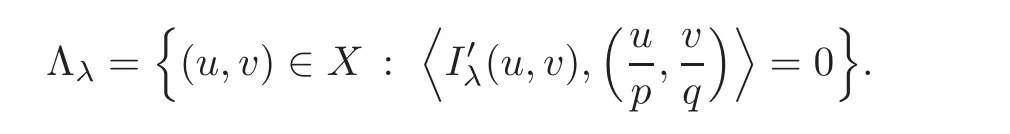
Clearly,Λλis a closed subset of X,and all critical points of Iλare in Λλ.We continue to call Λλa Nehari manifold even if Λλmay not be a manifold.It is easy to see that(u,v)∈ Λλif and only if

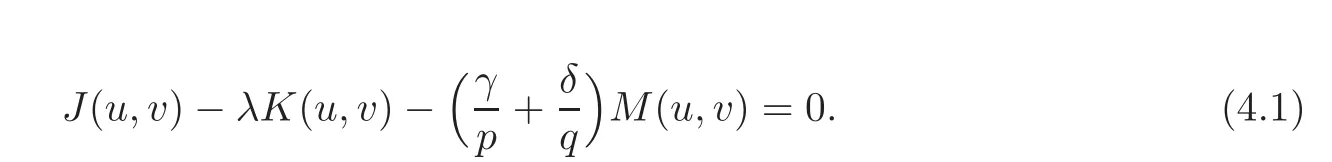
Hence,for(u,v)∈ Λλ,

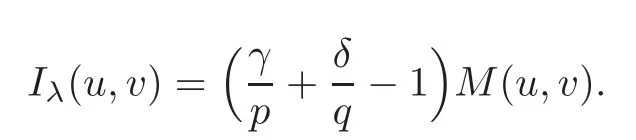
The Nehari manifold Λλcan be described by the Fibering mapping,defined for all t＞ 0 by

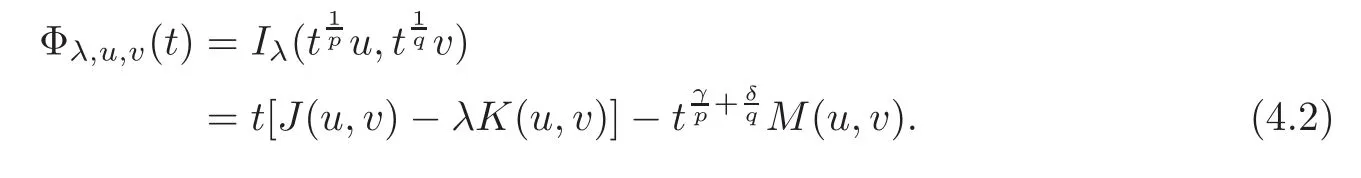
Therefore,for all t＞0,

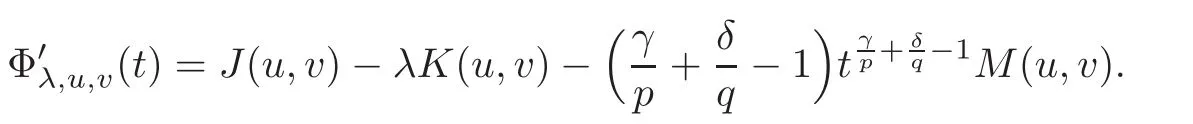
With this starting we are now in a position to prove the following lemma.

Lemma 4.1If(u,v)∈ X{(0,0)}andt＞ 0,then∈ Λλif and only ifΦ′λ,u,v(t)=0.

ProofThe result is an immediate consequence of the fact that

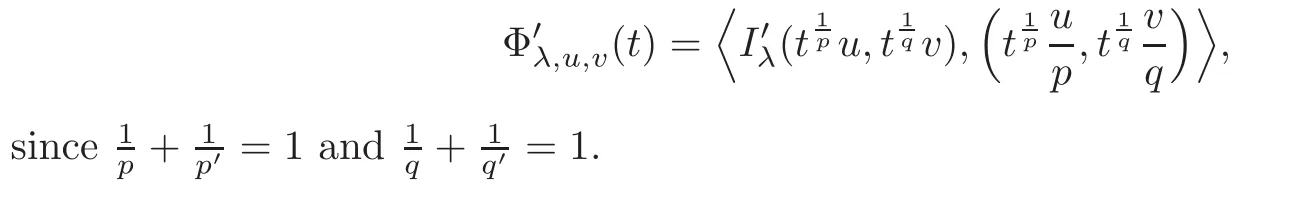
Remark 4.1From(t)=0,we obtain at once

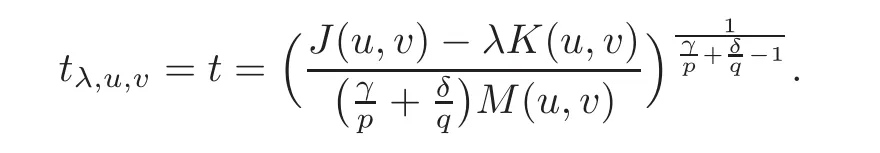
Hence,if(u,v)∈ X{(0,0)}and tλ,u,v＞ 0,then∈ Λλby Lemma 4.1.

The elements of Λλcorrespond to the stationary points of the maps Φλ,u,v(1)by Lemma 4.1,i.e.,

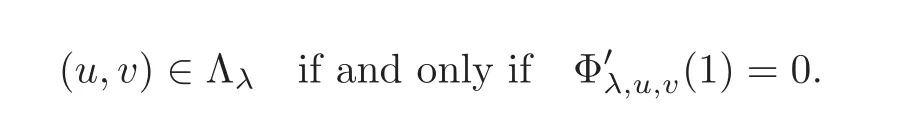
Hence it is natural to divide Λλinto three subsetscorresponding to the local minima,the local maxima and the saddle points of thefibering mapping.In other words,

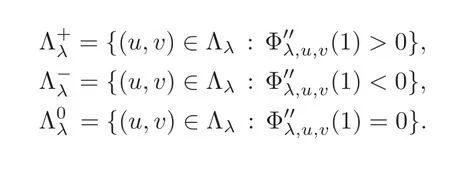
Now

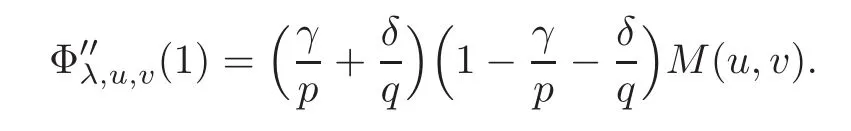
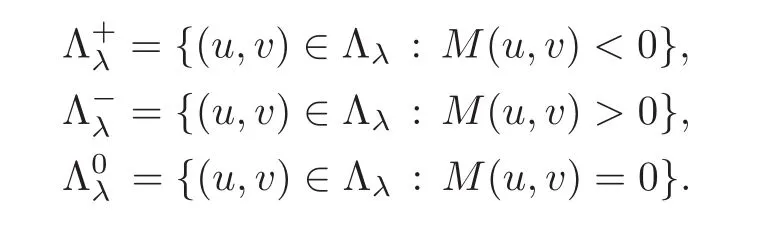
We shall prove the existence of solutions of problem(1.4)by investigating the existence of minimizers of the functional Iλon Λλ.Although Λλis a small subset of X,we shall see that local minimizers on the Nehari manifold Λλare the usual critical points of Iλin X.Indeed,we have the following result.

Lemma 4.2If(u0,v0)is a local minimizer ofIλonΛλand(u0,v0)/∈,then(u0,v0)is a critical point ofIλinX.

ProofIt is enough to use the same method used in the proof of[4,Lemma 2.2]to obtain the desired conclusion,with obvious changes.

To achieve a detailed characterization of the sets,and,we start by proving a lemma.

Lemma 4.3For anyλ,with0＜ λ ＜ λ1,there exists a constantµλ＞ 0such that

for all(u,v)∈X{(0,0)}.

ProofOtherwise,for any n∈N there exists(un,vn)∈X{(0,0)}such that

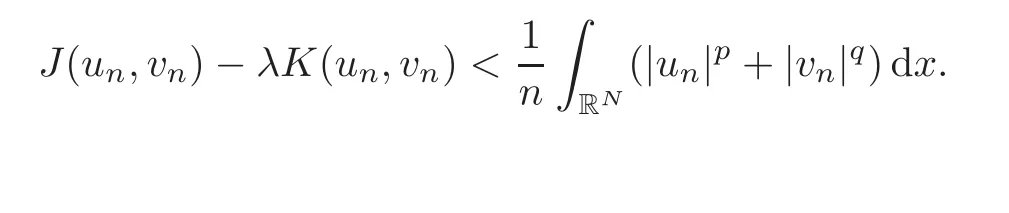
which is the required contradiction.

Now,if λ ∈ (0,λ1)Lemma 4.3 ensures that= Ø and={(0,0)}by(4.1)and(4.3).Therefore,Λλ=∪ {(0,0)},and Iλ(u,v)＞ 0 for all(u,v)∈Hence,in−fIλ(u,v)≥ 0.

Λλ

Lemma 4.4If0 ＜ λ ＜ λ1,thenIλis coercive onΛλ.

Fix λ ∈ (0,λ1).For all(u,v)∈ Λλ,using(4.1)and(4.3),we have

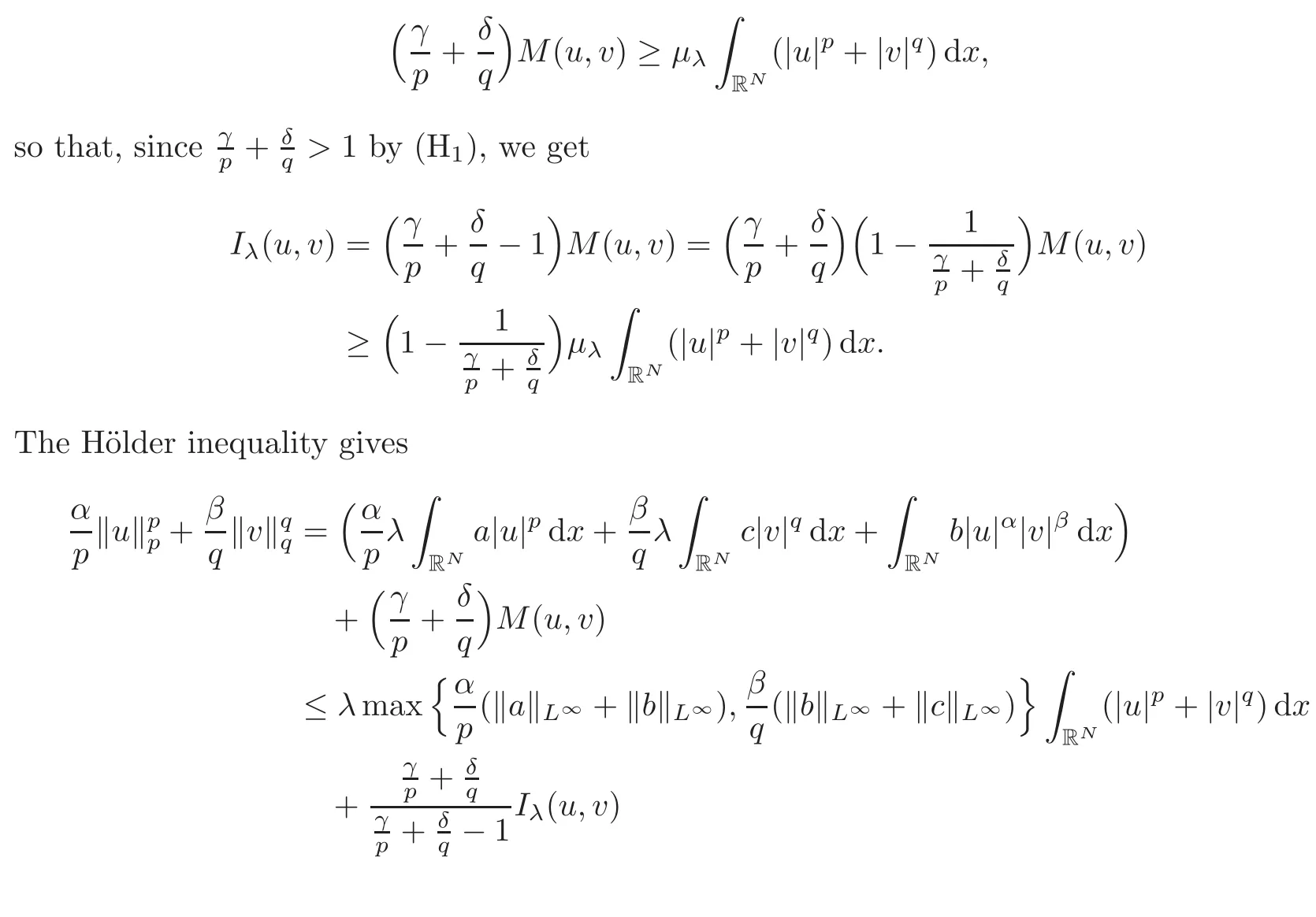
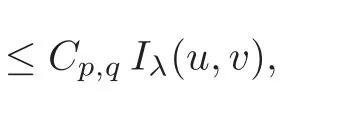
where

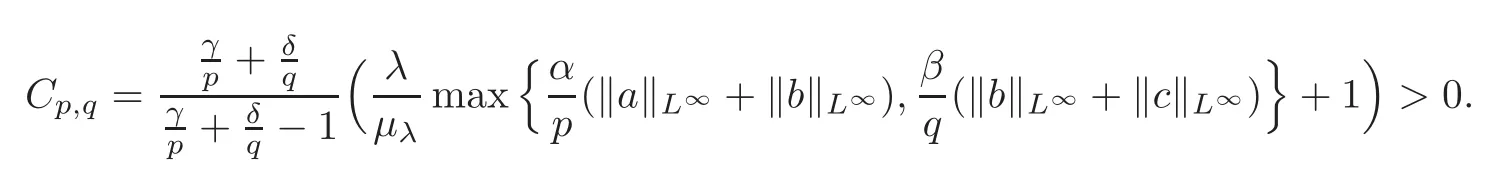
Hence Iλis coercive on Λλ.

Theorem 4.1Assume that(H1)–(H3)hold and let0＜ λ ＜ λ1.Then there exists a positive solution of problem(1.4).

ProofLet{(un,vn)}n⊂be a minimizing sequence of Iλin,i.e.,

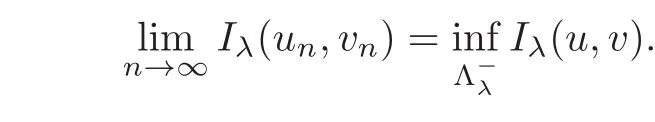
Since Iλis coercive in Λλ=∪ {(0,0)}by Lemma 4.4,{(un,vn)}nis bounded in X.Thus,passing if necessary to a subsequence still denoted by{(un,vn)}n,we get(un,vn)⇀(u0,v0)in X for some(u0,v0)∈X.Again un→u0in Lp(RN)and vn→v0in Lq(RN)by Lemma 2.1(1).Passing if necessary to another subsequence,we assume that

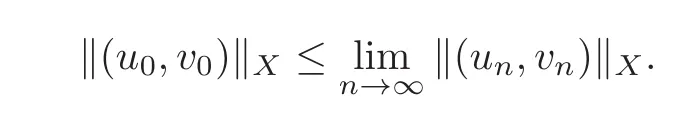
Hence,in particular,

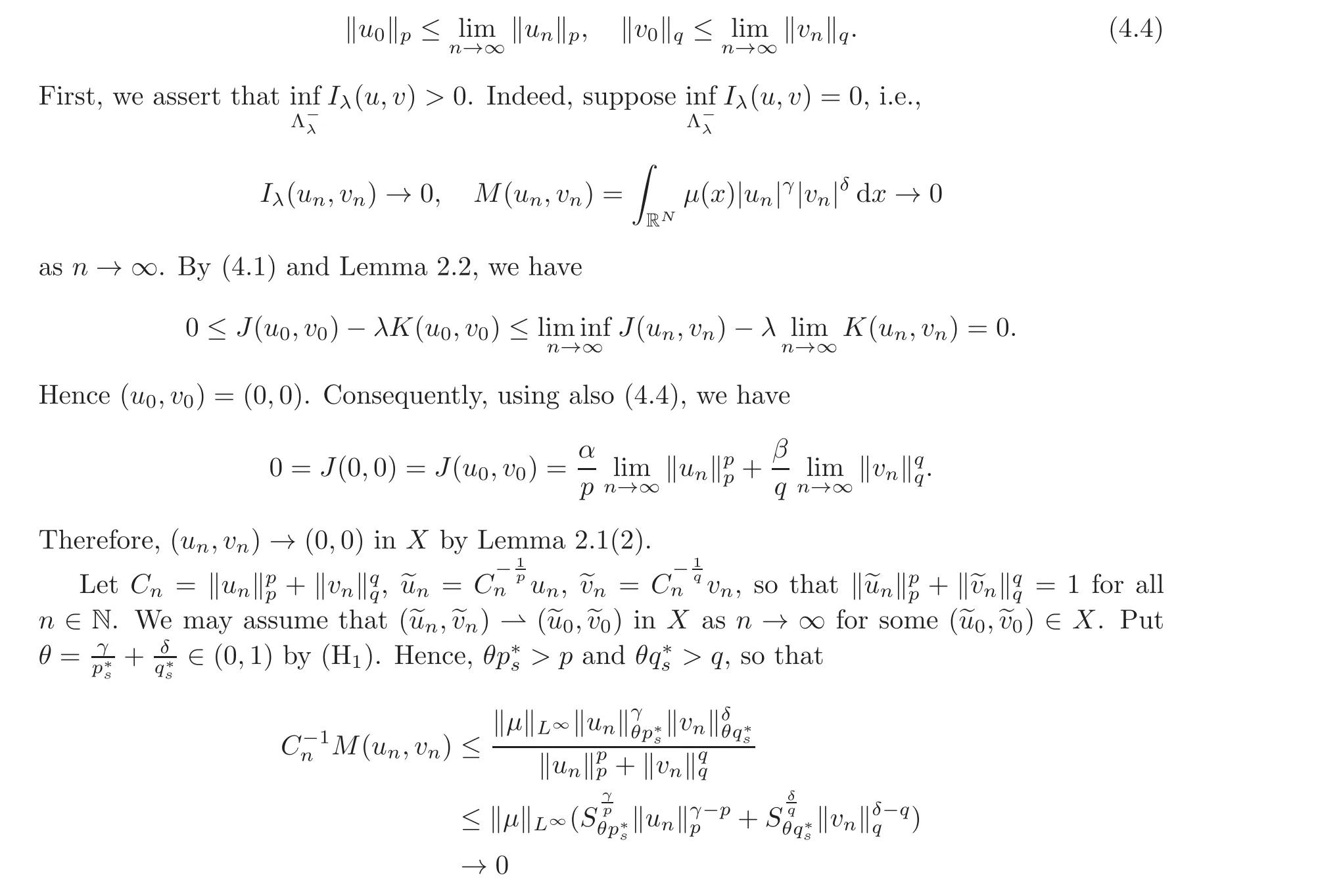
as n→∞,since 1＜p＜γ and 1＜q＜δ by(H1).By(4.1),we get

which is a contradiction.Consequently,(un,vn)→(u0,v0)in X as n→∞.

Lemma 4.3 implies that(u0,v0)is a critical point of Iλ(u,v)in X.Since Iλ(|u|,|v|)=Iλ(u,v)for all(u,v) ∈ X,the solution(u0,v0)must be nonnegative in Ω.Again,as explained in the proof of Theorem 3.1,the strong maximum principle,given in[14,Lemma 2.3]and in[15,Theorem 1.2],ensures that actually(u0,v0)is a positive solution of(1.4)in Ω by symmetry.

Theorem 4.2Assume that(H1)–(H3)and condition(1.6)hold.Ifλn→asn → ∞,then

Therefore,in(4.6)at least one inequality should hold with the strict sign by Lemma 2.1(2).Thus,

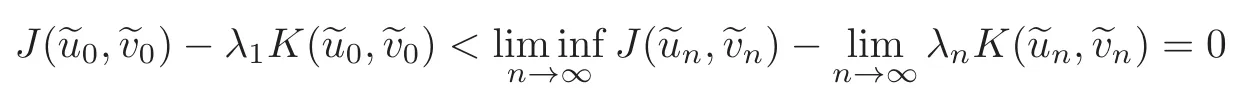
by Lemma 2.2.On the other hand,

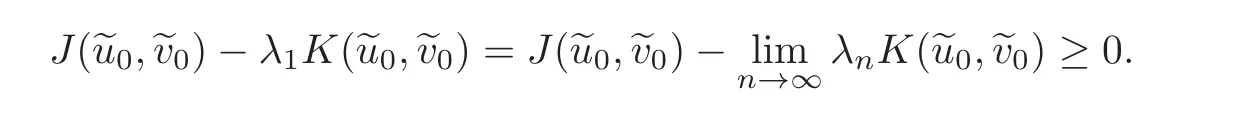
This contradiction implies the claim and soin X as n→∞.Therefore,we immediately obtain

Letting ε→ 0+,we obtain

that is,

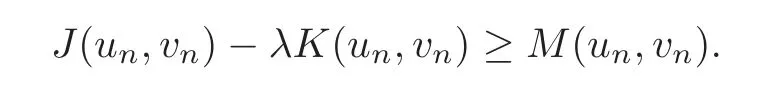
Since{(un,vn)}nconverges to(u,v)in X,

as n→∞.Hence

that is λ ＜ λ1.This is impossible since λ ≥ λ1by assumption.The proof is now complete.

AcknowledgementThis paper was started while Y.Fu was visiting the Dipartimento di Matematica e Informatica of the Universit`a degli Studi di Perugia,Italy,in June and July 2016 and was completed when P.Pucci was visiting the Department of Mathematics of the Harbin Institute of Technology at Harbin,China,in July 2017.Both authors thank the departments for the hospitality.

[1]Franzina,G.and Palatucci,G.,Fractional p-eigenvalues,Riv.Math.Univ.Parma,5(2),2014,373–386.

[2]Iannizzotto,A.and Squassina,M.,Weyl-type laws for fractional p-eigenvalue problems,Asymptot.Anal.,88(4),2014,233–245.

[3]Brown,K.J.and Zhang,Y.,The Nehari manifold for a semilinear elliptic equation with a sign-changing weight function,J.Differential Equations,193(2),2003,481–499.

[4]Chen,W.and Deng,S.,The Nehari manifold for a fractional p-Laplacian system involving concave-convex nonlinearities,Nonlinear Anal.Real World Appl.,27,2016,80–92.

[5]Zhang,G.,Liu,X.and Liu,S.,Remarks on a class of quasilinear elliptic systems involving the(p,q)-Laplacian,Electron.J.Differential Equations,2005(20),2005,10 pages.

[6]Goyal,S.and Sreenadh,K.,Existence of multiple solutions of p-fractional Laplace operator with signchanging weight function,Adv.Nonlinear Anal.,4(1),2015,37–58.

[7]Fiscella,A.,Pucci,P.and Saldi,S.,Existence of entire solutions for Schrö dinger-Hardy systems involving two fractional operators,Nonlinear Anal.,158(2),2017,109–131.

[8]Di Castro,A.,Kuusi,T.and Palatucci,G.,Local behavior of fractional p-minimizers,Ann.Inst.H.Poincar´e Anal.Non Lin´eaire,33(5),2016,1279–1299.

[9]Di Nezza,E.,Palatucci,G.and Valdinoci,E.,Hitchhiker’s guide to the fractional Sobolev spaces,Bull.Sci.Math.,136(5),2012,521–573.

[10]Grisvard,P.,Elliptic Problems in Nonsmooth Domains,2nd ed.,With a Foreword by Susanne C.Brenner,Classics in Applied Mathematics,69,Society for Industrial and Applied Mathematics(SIAM),Philadelphia,PA,2011.

[11]Pucci,P.,Xiang,M.and Zhang,B.,Multiple solutions for nonhomogeneous Schrö dinger-Kirchhoff type equations involving the fractional p-Laplacian in RN,Calc.Var.Partial Differential Equations,54(3),2015,2785–2806.

[12]Drabek,P.,Stavrakakis,N.M.and Zographopoulos,N.B.,Multiple nonsemitrivial solutions for quasilinear elliptic systems,Differential Integral Equations,16(12),2003,1519–1531.

[13]Amghibech,S.,On the discrete version of Picone’s identity,Discrete Appl.Math.,156(1),2008,1–10.

[14]Mosconi,S.and Squassina,M.,Nonlocal problems at nearly critical growth,Nonlinear Anal.,136,2016,84–101.

[15]Del Pezzo,L.M.and Quaas,A.,A Hopf’s lemma and a strong minimum principle for the fractional p-Laplacian,J.Differential Equations,263(1),2017,765–778.