Internal Controllability for Parabolic Systems Involving Analytic Non-local Terms

Pierre LISSY Enrique ZUAZUA

(This article is dedicated to Phillippe G.Ciarlet in the occasion of his 80th birthday,with gratitude and admiration for his mastery and continuous support.Merci Philippe!)

1 Introduction

1.1 Motivation

Nonlocal parabolic systems are relevant in a variety of applications to Biology and Physics(see[24]).They have been analyzed exhaustively in the recent past,in particular in the context of the non-local fractional Laplacian,and significant progress has been achieved.But controllability issues for these models remain very much unexplored.Here we analyse parabolic systems coupled by non-local lower order perturbations,the principal part being a classical constant coefficient parabolic system.

The content of this paper is a natural combination of the methods developed in[21]to achieve sharp results for parabolic systems coupled through constant coefficient matrices and those in[15]devoted to scalar equations perturbed by non-local lower order potentials.Our goal here is to derive a simple and exploitable spectral necessary and sufficient condition of controllability and the corresponding dual observability one.

This paper is very much inspired in the pioneering ideas introduced by J.L.Lions in his famous SIAM Review article[19]that stimulated a significant step forward on the state of the art.The early developments in thisfield were summarized with mastery in the celebrated survey article by D.L.Russell[25].The presentation in this paper is concise,relying significantly on various tools of functional analysis that are developed and presented in a self-contained manner in the more recent book by Phillippe G.Ciarlet[7].

1.2 Problem formulation and main result

Let us now present the problem under consideration into more details.

Let Ω be a smooth domain of RN(N ∈N∗),T ＞ 0,n∈N∗and m ∈ N∗(with possibly m ＜ n).Let ωi(i ∈ [|1,m|])be some open subsets of Ω that can be chosen arbitrarily(in particular all the ωi’s may be disjoint).

We are interested in the controllability of the following system of heat equations with Dirichlet boundary conditions:

with Y0∈ [L2(Ω)]n,u=(u1,···,um)∈ [L2(Ω)]m(which play the role of distributed controls),A ∈ Mn(H)⊂ Mn(L2(Ω × Ω))(where H is a space of admissible potentials that will be introduced afterwards in(1.12)),Bibeing the i-th column of B∈Mn,m(R).

The coupling matrix D∈Mn(R)is assumed to satisfy the ellipticity condition

(here and hereafter,‖·‖will always denote the euclidean norm).Condition(1.2)is sufficient to ensure the well-posedness of(1.13),since the principal part DΔ in(1.13)is strongly parabolic in the sense of[17,Chapter 7,Definition 7].

More precisely,we consider the so-called null controllability problem,the goal being to drive the system to the nullfinal target Y(T)≡ 0 by a suitable choice of the controls u=(u1,···,um)∈ [L2(Ω)]m.

The scalar case(i.e.,n=1)has been analyzed in[15]for a scalar potential a∈H.Our goal here is to extend those results to coupled systems,obtaining a simple and exploitable spectral necessary and sufficient condition of controllability and the corresponding dual observability one.

The controllability and observability of systems of partial differential equations have been intensively studied in the last decade,leading to important progress.We shall refer to some of the existing literature in the end of this introduction.But,as indicated above,the number of articles devoted to non-local problems is very limited.

Our analysis will follow a combination of the methods developed in[21]for the analysis of parabolic systems and in[15]to handle non-local coupling terms.Accordingly,we shall use in an essential manner the spectral decomposition of the Laplacian.

Let{λk}k≥1be the eigenvalues of−Δ with Dirichlet boundary conditions and ek∈ H10(Ω)be the corresponding eigenfunctions,constituting an orthonormal basis of L2(Ω).

Before considering the non-locally perturbed case,let usfirst recall some recent results on models involving constant coefficient coupling terms:

where Z0∈(L2(Ω))nand A∗∈ Mn(R)is a constant coupling matrix.

Here,rather than dealing with the controllability problem we consider the dual observability one.It concerns the obtention of full estimates on the state Z at time t=T out of partial measurements on the control subsets ωi.

In[21]it was proved that system(1.3)is observable on(0,T)in the sense that there exists C=C(T)＞ 0 such that for every Z0∈ [L2(Ω)]n,the solution Z of(1.3)verifies

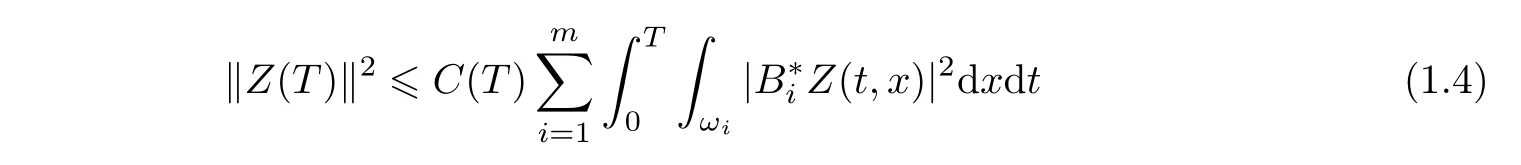
if and only if

where

Moreover,following[21,Proof of Theorem 3]and[23,Proof of Theorem 2.2],a precise upper bound on the observability constant C(T)in(1.4)can be given for T＞0 small enough,getting

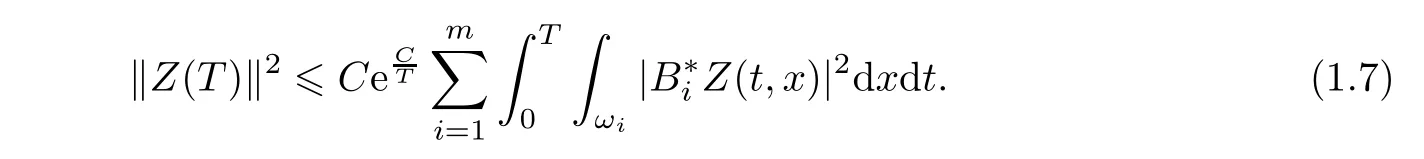
If A∗=0,it is easy to prove that(1.6)is equivalent to the following Kalman rank condition:

where,by definition,

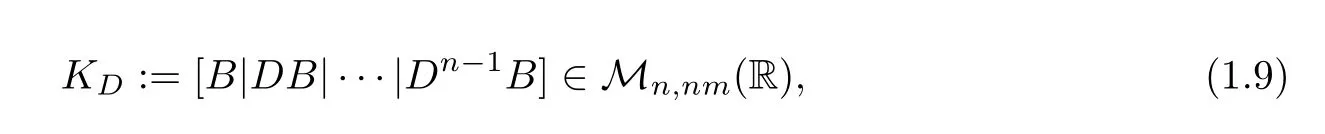
that only concerns the coupling matrix D and the control one B.When A∗/=0 though,we get a sequence of spectral conditions,depending on the eigenvalues of the Laplacian.

In all what follows,we decompose the initial condition as

where(Zk)k∈N∗ ∈ (l2(N∗))n.

The observability inequality(1.7),as pointed out in[16,Remark 6.1]?see also[23,Lemma 3.3]with β =1 and α =）,can be rewritten,in terms of the Fourier series expansion of the initial datum Z0given in(1.10),as

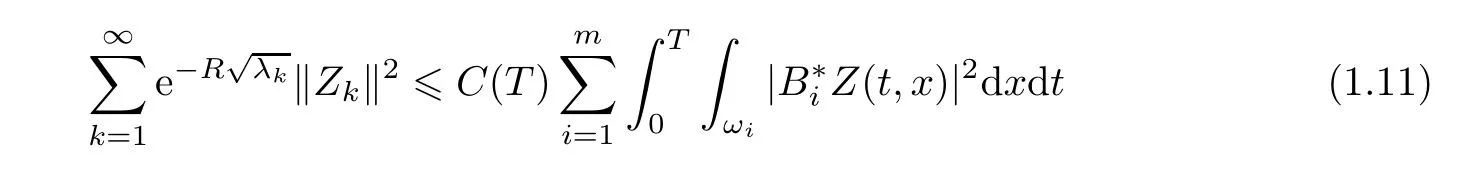
for some R＞ 0 and C(T)＞ 0 independent of Z0∈ [L2(Ω)]n.

Note that this kind of observability inequality(which is related to reachability issues,see e.g.[12]),introduced in[16],has also been used in[15,Lemma 2],for instance,to deal with non-local perturbations.Note also that estimating R in(1.11)and,more precisely,finding explicit lower bounds on R(in terms for instance of the geometries of Ω,ωiand the coupling matrices D and A)is an open problem,related to the optimal weights that can be considered in a Carleman estimate for the solutions of(2.1)(see[16]and Lemma 2.1 below),which are not known in general.This constitutes a challenging problem,also related to the cost of controllability and its dependence with respect to the geometry,which is still unknown in dimension greater than 1.Summarizing,the constant R＞0 so that(1.11)holds is known to exist,but very little is known on its actual value and its dependence on the parameters of the system under consideration.

This spectral observability inequality motivates the introduction of the following Hilbert space of non-local potentials(that was mentioned before when describing the class of models under consideration)

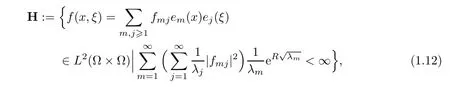
R＞0 being as in(1.11).Let us emphasize that kernels A∈Mn(H)enjoy the following property(see for instance[15,Remark 5]):

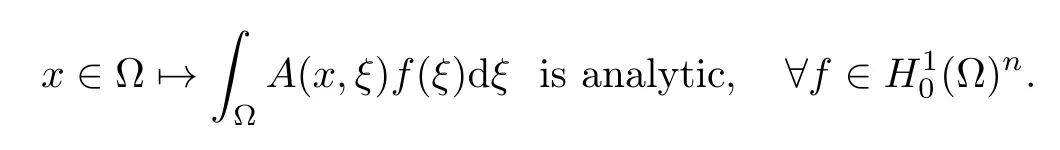
Let us now consider the following(forward)adjoint system of(1.1)involving also the nonlocal coupling terms:

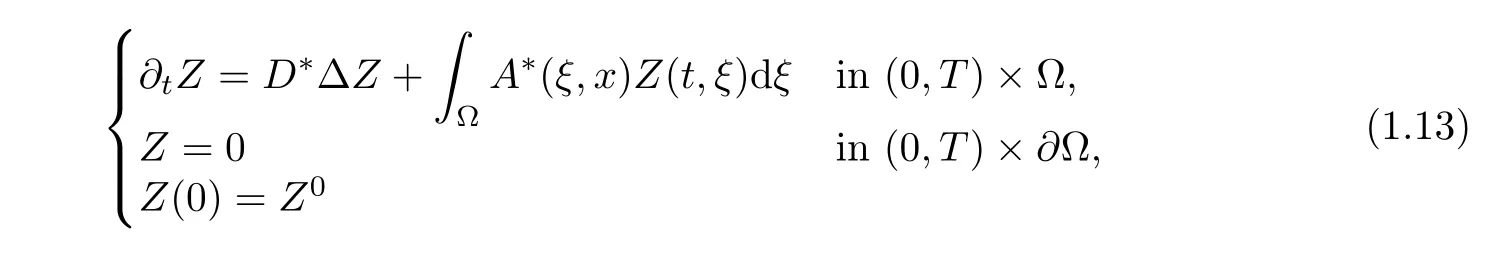
for some Z0∈ (L2(Ω))n.

Our goal is to extend the observability inequalities above for this complete model involving the non-local perturbations.We are able to reduce the observability problem under consideration to a unique continuation property for an elliptic problem,usually called Fattorini’s Criterion(see[13]).This condition is much easier to be verified in practice,as illustrated by two examples in Section 3.Note however that,due to the presence of the non-local term,this property is not a consequence of the existing wide literature on the unique continuation for elliptic problems and that analyticity assumptions are imposed on the kernel.As a consequence of the spectral observability inequality,by duality,we shall also derive the controllability property for the original control system involving the non-local terms.

The main result of this paper is the following.

Theorem 1.1Consider any T ＞ 0 and assume that A(x,ξ)∈ Mn(H),where H is defined in(1.12),and that KDverifies the Kalman rank condition(1.8).

Then,there exists C(T)＞0 such that any solution Z of(1.13)(involving the non-local perturbation terms)verifies

if and only if the following unique continuation property is verified for every λ ∈ R:

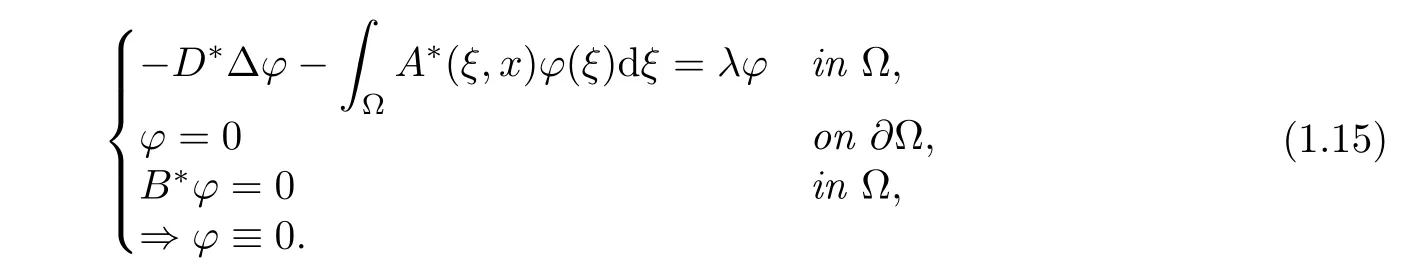
Equivalently,under condition(1.15),system(1.1)is null-controllable on(0,T),in the sense that for any Y0∈ [L2(Ω)]n,there exists u ∈ [L2((0,T)× Ω)]msuch that the corresponding solution to(1.1)verifies Y(T,·)=0.

The proof of the main result consists in obtaining the inequality(1.12)for the complete system(1.13)on the basis of the same inequality for the system in the absence of non-local perturbations(1.3).This is done applying a compactness-uniqueness argument,and reduces the issue to the fulfillment of the unique continuation property above(1.15)for the spectral problem.Once(1.12)is proved for the complete adjoint system(1.13),the null controllability result for(1.1)is a direct consequence of a classical duality principle.

Compactness-uniqueness arguments have rarely been applied in the context of heat equations because of the strong time irreversibility.In[15]this principle was applied in a satisfactory manner for scalar parabolic equations involving non-local potentials,provided they belong to the space H.This compactness-uniqueness technique,which applies in the context of nonlocal perturbation terms,cannot be used for pointwise space-varying coupling terms.The main novelty of the present article is to extend this analysis to parabolic systems involving non-local terms.

Several other remarks are in order.

Remark 1.1(1)We are unable to derive an explicit estimate on the cost of controllability in small time,similar to the one given in(1.7),because we use a contradiction argument.

(2)Remark that in(1.15),B∗ϕ =0 is assumed on all Ω and not only ω.This is a consequence of the analyticity properties of the kernel A∗.This fact facilitates the needed unique continuation property,which becomes a problem of an algebraic nature since localisation(in the space variable)issues do not arise.

(3)The hypothesis that A(x,ξ)belongs to Mn(H)is necessary in our study to develop the compactness-uniqueness argument.However,it is likely that this hypothesis to be of purely technical nature.In fact,there is no reason that A should be analytic,and it is likely that one might obtain the same result for any kernel that is regular enough to ensure that equation(1.1)is well-posed,for example A(x,ξ) ∈ Mn(L2(Ω × Ω)).Hence,a natural conjecture would be that the main result of Theorem 1.1 holds under the assumption that A(x,ξ)∈ Mn(L2(Ω×Ω))(instead of A(x,ξ)∈ Mn(H))and provided the unique continuation property(1.15)holds.

Note that in[22]a 1-d scalar equation is considered and that the analyticity assumption is avoided within the particular class of kernels in separated variables A(x,ξ)=Ax(x)Aξ(ξ),under the assumption that Ax(x)does not vanish in the subset where the control is being applied.On the other hand,as indicated by Patrick Gérard in a private communication,unique continuation may fail for the spectral problem with smooth kernels in separated variables of compact support even in the scalar case n=1.Accordingly it fails for time-dependent parabolic problems too.This example shows the necessity of some additional assumption on the kernel,such as analyticity,for the unique continuation property to hold even for scalar equations.Finding sharp conditions on the non-local kernel for unique continuation in the context of systems is an interesting open problem.

1.3 Bibliographical comments

As indicated above,there is an extensive literature devoted to the controllability properties of PDE systems but problems involving non-local terms are rarely considered.Apart from references[15]and[22],we would like to mention[20],where a Carleman estimate for a scalar non-local parabolic equation with an integral term involving the solution and itsfirst order derivatives is proved,with applications to unique continuation and inverse problems.

Concerning parabolic systems without non-local terms,some of the existing results concern the following topics and techniques(see also the survey[1]for earlier results).For a more detailed presentation,concerning also the hyperbolic and dispersive case,we refer to[21].

(1)One-dimensional results(i.e.,d=1)were obtained in[2—4,6].

(2)Multi-dimensional results were obtained in[10]for constant or time-dependent coupling terms,and partial results in the case of space-dependent coupling terms were obtained in[2—3,5—6,11,18].

(3)The nonlinear case was notably studied in[8—9,14].Internal Controllability for Parabolic Systems Involving Analytic Non-local Terms 287

(4)Observability properties for systems involving a superposition of different dynamics(notably coupled systems of heat and wave equations)were studied in[26].

2 Proof of the Main Result

Assuming that the spectral unique continuation property(1.15)is verified,the proof consists in showing that the null-controllability of(1.1)holds.To do this,using the equivalence between null controllability and observability,it suffices to show that the observability inequality(1.14)holds for the complete system(1.13).

The proof of this inequality for the complete system involving the non-local terms relies on a compactness-uniqueness argument similar to the one in[15,Proof of(16)].We proceed in several steps.

Step 1Splitting of the solution.To get(1.14),first of all,we decompose the solution Z of(1.13)into two parts Z= ζ+p,where p verifies

and ζ verifies

From(1.8)and(1.11),we already know that

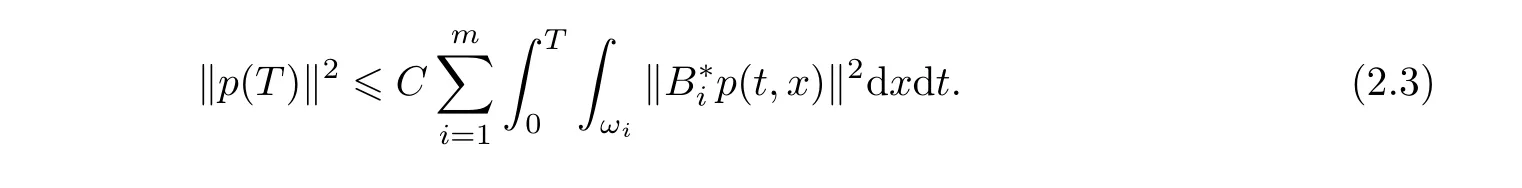
Step 2An auxiliary Carleman estimate.Let us prove the following useful Carleman estimate.

Lemma 2.1There exist two constants C0＞0(not depending on T)and C(T)＞0 such that for any Z0∈ [L2(Ω)]n,the solution p of(2.1)verifies

ProofWe follow the computations of[16,Remark 6.1].First of all,we decompose Z0in the Hilbert basis{ek}as

For C0＞0(to be determined later on)we remark that

Using the ellipticity condition(1.2),there exists C1＞0(independent of C1)such that for any t＞0,one has

Hence,from(2.5)and(2.7)we deduce that

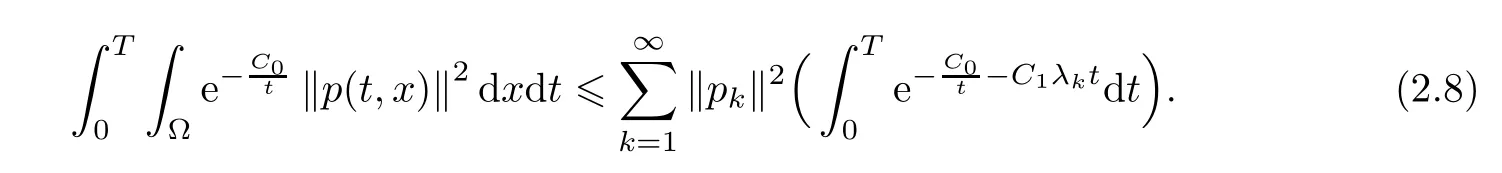
Besides,it is well-known that,as λ → ∞,

Hence,there exists some C2＞0 such that for any k＞0,one has

We deduce from(2.8)that

Inequality(2.4)then follows by using(1.11)together with(2.9)and taking C0large enough

Step 3Reduction to the proof of two inequalities.We remark that in order to obtain(1.14),it is enough to prove the two following key inequalities:

and

Step 4Proof of(2.10).Assume that(2.10)is not verified whereas(1.15)is verified.Then,there exists a sequence()n∈Nsuch that the corresponding solution pnof(2.1)with initial conditionverifies

and the corresponding solution Znof(1.13)with initial conditionis such that

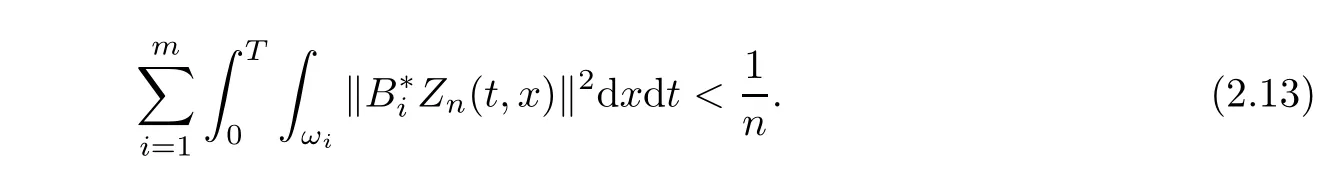
We also call ζnthe solution to(2.2)where p is replaced by pn,so that we have the relation

We are going to prove that ζn→ 0(up to a subsequence)strongly in L2((0,T)× Ω),which is obviously in contradiction with(2.12)—(2.13)since these estimates together with(2.14)imply

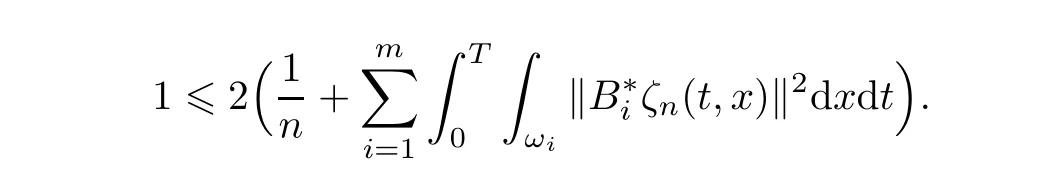
First of all,let us remark that there exists C＞0 such that

It is an easy consequence of the computation given in[15,(21)]applied on each component of A∗.Hence,by classical energy estimates and compactness arguments,one may assume that ζnconverges strongly in L2((0,T)× Ω)to some ζ∈ L2((0,T)× Ω).This implies,together with(2.4)and(2.14),that if we fix δ∈ (0,T),(Zn)n∈Nis bounded in L2((δ,T),Ω).Hence,(Zn)n∈Ncan be assumed to converge weakly in L2((δ,T),Ω)to some Z ∈ L2((δ,T),Ω).Then,one can prove that Z solves the following PDE:

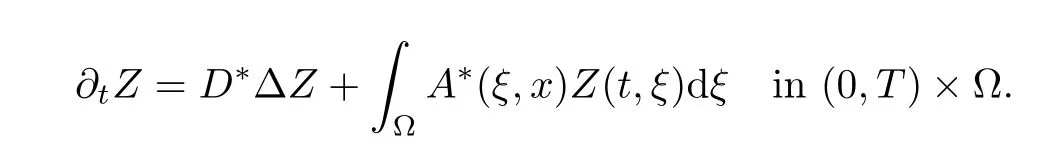
Moreover,we also know,thanks to(2.13),thatZ(t,x)=0 on(0,T)×ωi,∀i∈[|1,m|].Using the well-known Fattorini criterion for approximate controllability(see[13]),proving that Z≡0 is equivalent to proving the following assertion:

Hence,we consider any ϕ ∈ L2(Ω)verifying

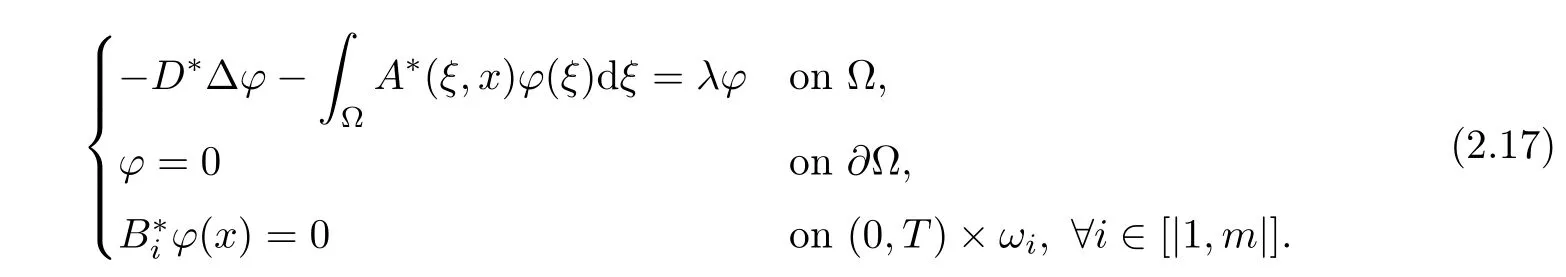
We will prove the following analyticity property on ϕ.

Lemma 2.2Any ϕ ∈ L2(Ω)verifying the first two lines of(2.17)for some λ ∈ R is analytic on Ω.

ProofFrom(2.17)and taking into account that x →RΩA∗(ξ,x)ϕ(ξ)dξ is analytic on Ω(hence C∞on Ω)since ϕ ∈(Ω),an easy induction argument gives that ϕ ∈ C∞(Ω).Now,consider any component of A∗that we call a∗and that we decompose as

Using condition(1.12)and since A∗∈Mn(H),we obtain that for any j∈N,one has

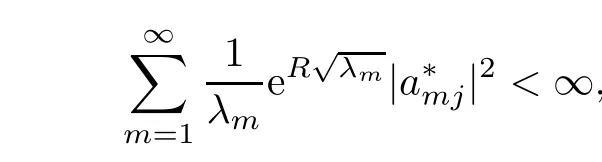
implying thanks to(2.17)that for any ϕ ∈(Ω)n,one has K(ϕ)=0 on ∂Ω,where K is given by

Hence,another easy induction argument enables us to conclude that

where Δ represents here the Dirichlet Laplace operator with domain(Ω)∩ H2(Ω).Let us now prove that ϕ is moreover analytic.Let k ∈ N.In what follows,C is a constant that may vary from inequality to inequality and is independent of k.We consider the scalar product of the first line of(2.17)by the vector Δ2k+1ϕ and we integrate on Ω.Taking into account(2.18),we obtain after some integrations by parts that

so that notably

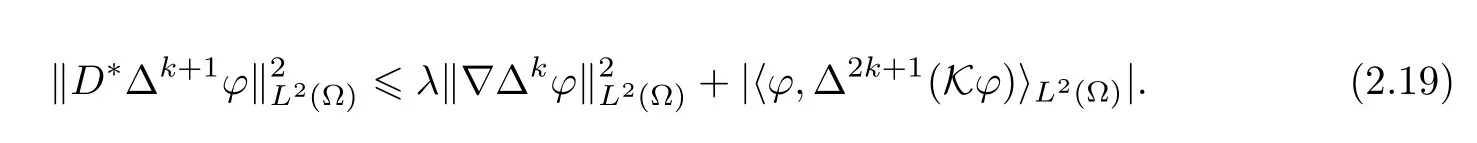
Let us focus on ‖Δ2k+1(Kϕ)‖L2(Ω).Following the computations of[15,Remark 5],one easily infers that for any component of A∗that we call a∗and that we decompose as a∗(ξ,x)=

where for any multi-index α =(α1,···,αN),we write for simplicity|α|= α1+ ···+ αNand∂αϕ =It is well-known that inequality(2.24)implies the analyticity of ϕ on Ω,whichfinishes the proof.

We are now ready to complete the proof of Step 4.Let us consider any ϕ ∈ L2(Ω)Nverifying(2.17).Using Lemma 2.2,we deduce that ϕ is analytic on Ω,which implies that B∗ϕ is also analytic on Ω.Hence,using the last line of(2.17),we deduce that B∗ϕ =0 in Ω.

Now,using assumption(1.15),(2.16)is verified and hence Z ≡ 0 on(0,T)× Ω.We deduce that pnconverges weakly to−ζ in L2((0,T)×Ω),which implies that ζn→ 0= ζ in L2((0,T)×Ω)because of(2.2).This leads to the desired contradiction.

Step 5Proof of(2.11).This inequality is a consequence of(2.3)and easy energy estimates on ξ using equation(2.2)and arguing as in the proof of[15,(21)].

Finally,we have proved that(1.15)implies(1.14).The fact that the null-controllability of(1.1)(i.e.,(1.14))implies(1.15)is standard and is omitted.

3 Two Simple Examples of Application

3.1 Indirect controllability of cascade systems of two equations

In what follows,we consider the case of two coupled equations with cascade structure and control on thefirst component.

More precisely,we consider the following system:

Here D is given by

and is assumed to verify(1.2).The non-local potential A is given by

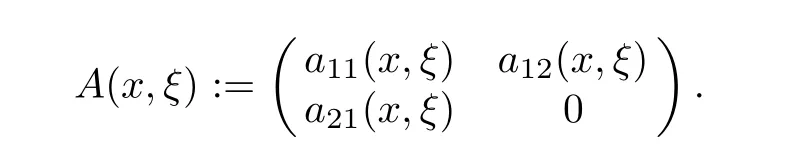
We consider the control operator B given by

The control acts on some open subset ω ⊂ Ω.We are going to prove the following sufficient condition for the controllability of(3.1).

Theorem 3.1Consider any T＞0 and assume that aij(x)∈H for(i,j)∈{1,2}2,d21/=0 and d22/=0.Then,(3.1)is null-controllable.

ProofFirst,observe that condition(1.8)is equivalent to d21/=0.Then,applying Theorem 1.1,the null-controllability of(3.1)is equivalent to the following unique continuation property:

By contradiction,assume that there exists some ϕ /≡ 0 verifying the first three equations of(3.2).Let us decompose a21as follows:from the second equation of(3.2)that there exists m ∈ N∗such that λ =d22λm.In this case,without loss of generality we may assume that ϕ(x)=em(x).Using the spectral decomposition of a21,we obtain that

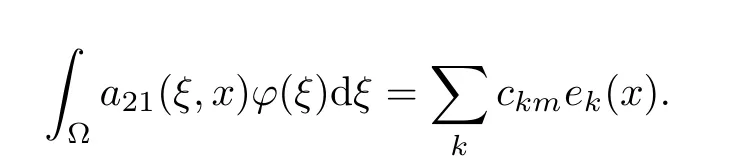
Moreover,one has −d21Δϕ(x)=d21λmem(x).Hence,we deduce that a21is necessarily such that the two following conditions are verified:

(1)ckm=0 if k/=m.

(2)cmm=d21λm.

The conclusion follows since such an a21cannot be in H in view of(1.12).

3.2 Simultaneous controllability of two equations with diagonal principal part

In what follows,we consider the case of two coupled equations with simultaneous control:

Here D is given by

where d11＞0 and d22＞0.A is given by

where aij(x)∈H for i,j=1,2.We consider the control operator B given by

The control acts on some open subset ω ⊂ Ω.

We are going to prove the following sufficient condition for the controllability of(3.3).

Theorem 3.2Consider any T＞0 and assume that aij(x)∈H for(i,j)∈{1,2}2,(i,j)/=(2,2)and d11/=d22.Then,(3.3)is null-controllable if the following conditions(for instance)are verified:

(1)a11=a21.

(2)a12and a22are symmetric in the variables(x,ξ).

ProofRemark that the Kalman rank condition(1.8)is verified here since d11/=d22and each component of B is nonzero.Hence,we can apply Theorem 1.1 and we obtain that the null-controllability of(3.3)is equivalent to the following unique continuation property:

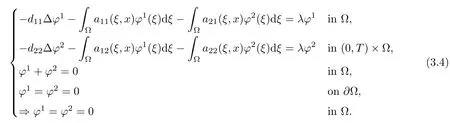
Substituting ϕ2in the first two equations of(3.4)and using the hypothesis a11=a21,we obtain that(3.4)is equivalent to

From the first line of(3.5)we may assume that λ ＞ 0(since every eigenvalue of the Laplace operator with Dirichlet boundary conditions is positive).We multiply thefirst line of(3.5)by d22and the second line of(3.5)by d11,and we subtract the result.We obtain that

We apply the Laplace operator to this equation,we use the symmetry of the coefficients a12,a22and we perform some integrations by parts.We obtain that

Now,we replace Δϕ1thanks to the first line of(3.5)and we obtain

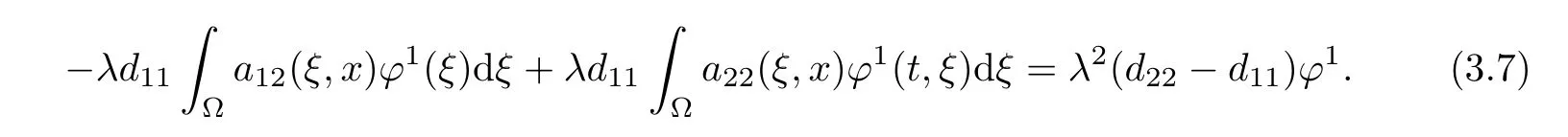
Multiplying(3.6)by λ and using(3.7)lead to ϕ1=0 since λ /=0 and d11/=d22,so that we also have ϕ2=0 by the third line of(3.4).

[1]Ammar-Khodja,F.,Benabdallah,A.,González-Burgos,M.and de Teresa,L.,Recent results on the controllability of linear coupled parabolic problems:A survey,Mathematical Control and Related Fields,1(3),2011,267–306.

[2]Ammar-Khodja,F.,Benabdallah,A.,González-Burgos,M.and de Teresa,L.,The Kalman condition for the boundary controllability of coupled parabolic systems,bounds on biorthogonal families to complex matrix exponentials,J.Math.Pures Appl.(9),96(6),2011,555–590.

[3]Ammar-Khodja,F.,Benabdallah,A.,González-Burgos,M.and de Teresa,L.,Minimal time for the null controllability of parabolic systems:The effect of the condensation index of complex sequences,J.Funct.Anal.,267(7),2014,2077–2151.

[4]Ammar Khodja,F.,Benabdallah,A.,González-Burgos,M.and de Teresa,L.,New phenomena for the null controllability of parabolic systems:Minimal time and geometrical dependence,J.Math.Anal.Appl.,444(2),2016,1071–1113.

[5]Benabdallah,A.,Boyer,F.,González-Burgos,M.and Olive,G.,Sharp estimates of the one-dimensional boundary control cost for parabolic systems and application to the N-dimensional boundary null controllability in cylindrical domains,SIAM J.Control Optim.,52(5),2014,2970–3001.

[6]Boyer,F.and Olive,G.,Approximate controllability conditions for some linear 1D parabolic systems with space-dependent coefficients,Math.Control Relat.Fields,4(3),2014,263–287.

[7]Ciarlet,P.G.,Linear and Nonlinear Functional Analysis with Applications,Society for Industrial and Applied Mathematics,Philadelphia,PA,2013.

[8]Coron,J.-M.,Guerrero,S.and Rosier,L.,Null controllability of a parabolic system with a cubic coupling term,SIAM Journal on Control and Optimization,48(8),2010,5629–5653.

[9]Coron,J.-M.and Guilleron,J.-P.,Control of three heat equations coupled with two cubic nonlinearities,SIAM J.Control Optim.,55(2),2016,989–1019.

[10]Duprez,M.and Lissy,P.,Indirect controllability of some linear parabolic systems of m equations with m−1 controls involving coupling terms of zero orfirst order,J.Math.Pures Appl.(9),106(5),2016,905–934.

[11]Duprez,M.and Lissy,P.,Positive and negative results on the internal controllability of parabolic equations coupled by zero and first order terms,J.Evol.Equ.,2016,1–22,DOI:10.1007/s00028-017-0415-1.

[12]Ervedoza,S.and Zuazua,E.,Sharp observability estimates for heat equations,Archive for Rational Mechanics and Analysis,202,2011,975–1017.

[13]Fattorini,H.O.,Some remarks on complete controllability,SIAM J.Control,4(4),1966,686–694.

[14]Fernández-Cara,E.,González-Burgos,M.and de Teresa,L.,Controllability of linear and semilinear nondiagonalizable parabolic systems,ESAIM Control Optim.Calc.Var.,21(4),2015,1178–1204.

[15]Fernández-Cara,E.,Lü,Q.and Zuazua,E.,Null controllability of linear heat and wave equations with nonlocal spatial terms,SIAM J.Control Optim.,54(4),2016,2009–2019.

[16]Fernández-Cara,E.and Zuazua,E.,The cost of approximate controllability for heat equations:The linear case,Adv.Differential Equations,5(4–6),2000,465–514.

[17]Ladyzenskaja,O.A.,Solonnikov,V.A.and Ural’ceva,N.N.,Linear and quasilinear equations of parabolic type,23,American Mathematical Society,Providence,R I.,1968.

[18]Léautaud,M.,Spectral inequalities for non-selfadjoint elliptic operators and application to the nullcontrollability of parabolic systems,J.Funct.Anal.,258(8),2010,2739–2778.

[19]Lions,J.-L.,Exact controllability,stabilization and perturbations for distributed systems,SIAM Rev.,30(1),1988,1–68.

[20]Lorenzi,A.,Two severely ill-posed linear parabolic problems,Alexandru Myller Mathematical Seminar,AIP Conf.Proc.,1329,Amer.Inst.Phys.,Melville,NY,2011,150–169.

[21]Lissy,P.and Zuazua,E.,Internal observability for coupled systems of linear partial differential equations,HAL,2017,https://hal.archives-ouvertes.fr/hal-01480301/document.

[22]Micu,S.and Takahashi,T.,Local controllability to stationary trajectories of a one-dimensional simplified model arising in turbulence,HAL,2017,https://hal.archives-ouvertes.fr/hal-01572317.

[23]Miller,L.,A direct Lebeau-Robbiano strategy for the observability of heat-like semigroups,Discrete Contin.Dyn.Syst.Ser.B,14(4),2010,1465–1485.

[24]Okubo,A.and Levin,S.A.,Diffusion and Ecological Problems:Modern Perspectives,Interdisciplinary Applied Mathematics,14,Springer-Verlag,New York,2001.

[25]Russell,D.L.,Controllability and stabilizability theory for linear partial differential equations:Recent progress and open questions,SIAM Rev.,20(4),1978,639–739.

[26]Zuazua,E.,Stable observation of additive superpositions of partial differential equations,Systems Control Lett.,93,2016,21–29.