Some Remarks on Korn Inequalities

Alain DAMLAMIAN

(Dedicated to Philippe G.Ciarlet on the occasion of his 80th birthday)

1 Introduction

In the joint paper with Doina Cioranescu and Julia Orlik[2],the homogenization of static linearized elasticity problems in the presence of cracks and inclusions was studied.This can be reduced to minimizing a convex functional but its coerciveness is not straightforward,mainly because of the presence of(infinitesimal)rigid motions.In the homogenization process,thefirst difficulty is to obtain uniform estimates.These are intimately connected with the uniform coerciveness of the convex functionals involved.

There are multiple “classical”results on unilateral contact.Many works of Gaetano Fichera[5—8]are the first concerning the existence of solutions for such problems.More recently,the following books consider this problem:Hlav´aˇcek,I.,Haslinger,J.,Neˇcas,J.and Lov´ıˇcek,J.[11](1982),Kikuchi,N.and Oden,J.T.[12](1988),Eck,C.,Jaruˇsek,J.and Krbec,M.[4](2005).

All these results give conditions under which a solution exists,but none give explicit estimates which,in the case of homogenization,would be uniform with respect to the homogenization parameter.Furthermore,none seem to treat the case of Tresca friction for inclusions or cracks.In[2],the problem was solved byfirst proving a unilateral Korn inequality adapted to inclusions.

Section 2 of this paper presents some definitions related to the classical Korn inequalities.In Section 3,we give a procedure to construct Korn inequalities starting from“semi-norm-like functions”on the space of rigid motions.Section 4 gives examples.For simplicity,they are set in the natural space R3but extensions to higher dimensions are straightforward.

NotationsLet v be a vectorfield on a domain of R3and S an orientable surface therein1All surfaces in this paper are assumed to be orientable.;

• a choice of unit normal vector to the surface S is denoted ν (the other would be −ν),the scalar normal component of v on S is v·ν,denoted vν,its tangential component v−vνν is denoted vτ;

• ∇v is the gradient of v,defined as the matrix field:

•e(v)is the strain tensor(symmetric gradient)of v,defined as the symmetric matrix field:

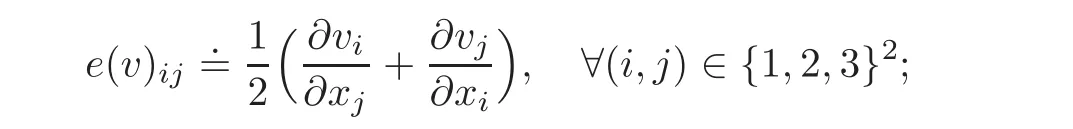
• R is the kernel of e in connected domains,i.e.,the space of infinitesimal rigid motions:

In the case of R3(or an open connected subdomain in R3),this is also

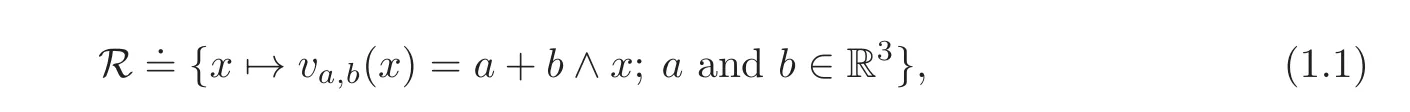
where∧indicates the vector product(i.e.,cross product or wedge product)in R3;

•in estimates,C is a generic constant(function of the domain only);

• for a given domain O of R3,the spaces of scalarfields,vectorfields and matrix fields L2(O;R),L2(O;R3)and L2(O;R9),will all be referred to as L2(O)(there will be no ambiguity from the context).Similarly,the spaces of scalarfields and vectorfields H1(O;R)and H1(O;R3)will often be denoted simply H1(O).The latter is endowed with the norm

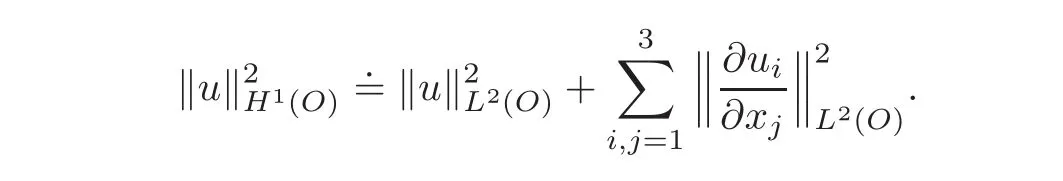
2 Korn Domains and Korn-Wirtinger Domains

Korn inequalities are inequalities bounding the L2-norm of the gradient of a vectorfield in a domain(or its H1-norm)by that of its symmetric gradient together with some extra terms,if necessary.

Thefirst Korn inequality is classical for the spaceof any domain.

Proposition 2.1LetObe an open set inR3.Then for everyuin(O),

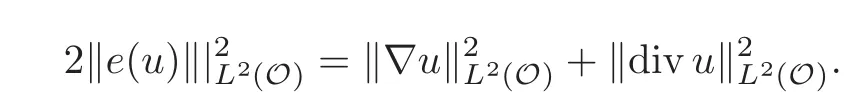
Consequently

and if the Poincar´e inequality holds inOwith the constantCP(O)(e.g.,Ois bounded in one direction)

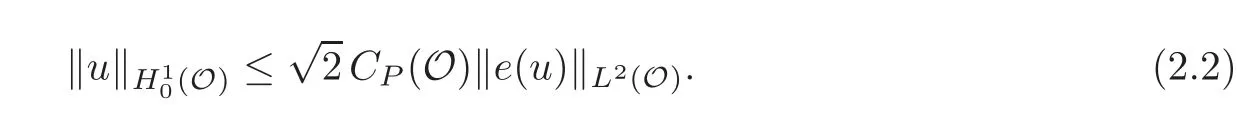
ProofUsing the summation convention and the Stokes formula(for the cross terms)

Definition 2.1A domainOis a Korn domain if the second Korn inequality holds forH1(O),i.e.,there exists a constantCK(=CK(O))such that

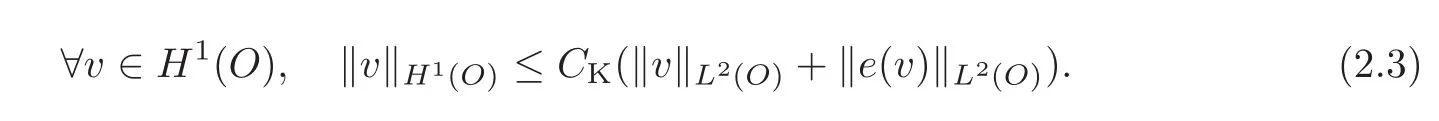
In 1962,Gobert[9]gave thefirst proof that a bounded domain with Lipschitz boundary is a Korn domain.More recent proofs(none of them straightforward)can be found in the book[13]of Oleinik,Shamaev and Yosifian and the paper[1]of P.Ciarlet and P.G.Ciarlet.

It is obvious that the union of afinite number of Korn domains is a Korn domain.This is the case of domains with afinite number of Lipschitz cracks provided the cracks which touch the boundary are not tangent to it.

The following is the analogue for vectorfields of the Poincar?-Wirtinger inequality for scalar functions.

Definition 2.2A bounded connected open domainOis a Korn-Wirtinger domain if there exists a constantCKW(=CKW(O))such that for everyvinH1(O)there is anr(v)inRwith

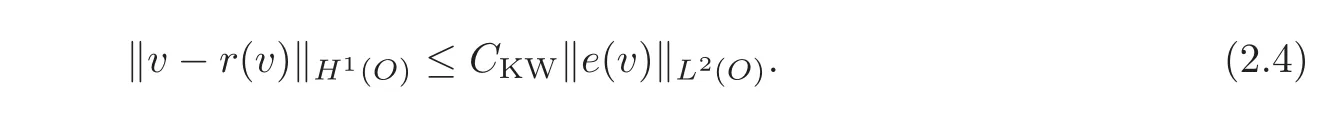
Obviously,r(v)can be chosen as the orthonormal projection ofvonRin the Hilbert spaceH1(O)so thatris linear andv−r(v)is orthogonal toR.

Remark 2.1It is straightforward to check that the Poincar?-Wirtinger for scalar functions holds in H1(O)when O is a Korn-Wirtinger domain(it suffices to consider vectorfields with only one non-zero component).The converse seems open.2The converse for certain weighted norms is a consequence of Theorem 2.3 of[10].

The following proposition gives examples of Korn-Wirtinger domains.

Proposition 2.2Suppose thatOis a connected and bounded Korn domain.If the natural injection fromH1(O)toL2(O)is compact,then,Ois a Korn-Wirtinger domain.This is true in particular as soon as the boundary ofOis Lipschitz.

The proof is classical but we give it for the sake of completeness.

ProofBy contradiction,if(2.4)holds for no constant CKW,then one can construct a sequence{un}n∈Nin the orthogonal complement of R in H1(O)such that

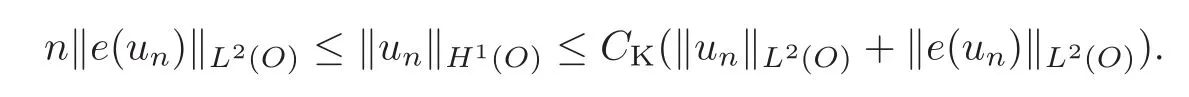
By scaling,one can assume that‖un‖L2(O)≡ 1.

Remark 2.2As is expected in a proof by contradiction,the constant C is not explicit.The same is true for every statement below.

Here is a way to obtain more Korn-Wirtinger domains.

Proposition 2.3The union of two Korn-Wirtinger domains whose intersection is not empty is a Korn-Wirtinger domain.The same holds true for two Korn-Wirtinger domains whose boundaries intersect along a subset which contains a portion of a Lipschitz hypersurface with non-zero superficial measure.This can be generalized to afinite union of Korn-Wirtinger domains.

ProofLet u be in H1(O)with O=O1∪O2.The hypotheses imply that there exist two rigid motions r1and r2such that

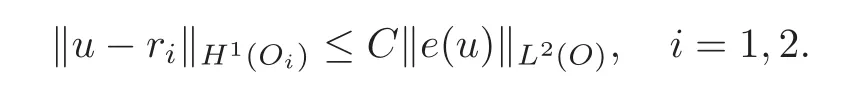
In particular,

and consequently,

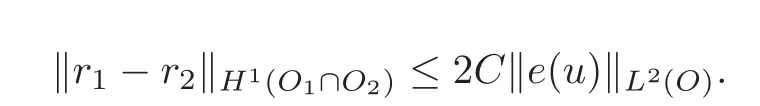
Since all the norms are equivalent on thefinite dimensional space R,it is also true that

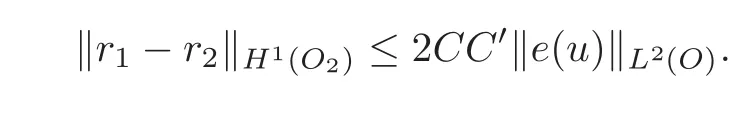
Consequently,

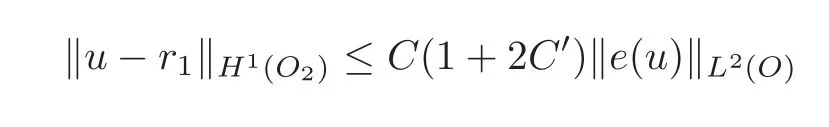
and

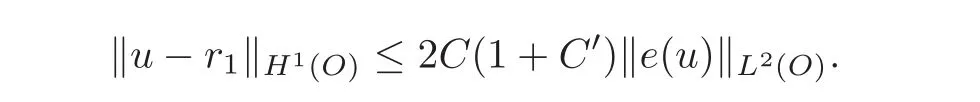
In the second case denoting Σ a part of the common boundary which is included in a Lipschitz hypersurface and withfinite measure,the proof is the same but makes use of the trace theorem from H1(Oi),i=1,2,to L2(Σ)(instead of the restriction from H1(Oi))to H1(O1∩O2)).

3 Construction of Korn Inequalities

The point of Korn inequalities is that there is no single one which can be applied in every problem.Each problem requires an adapted Korn inequality.Here is a method to generate Korn inequalities on Korn-Wirtinger domains.The constants exist but are not very easy to track.Sharper estimates of the constant in each case may be of interest but is out of the scope of this paper.

Theorem 3.1LetObe a Korn-Wirtinger domain.IfF:H1(O))→Ris a Lipschitz map whose restriction to the subspaceRof rigid motions is bounded below by a norm onR.Then there exists a constantCsuch that

ProofLet u be in H1(O)and r(u)be an element in R such that(2.4)holds.By the hypothesis on F,it follows that

Since all norms are equivalent on R,this implies

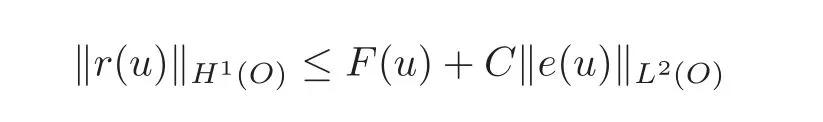
and going back to(2.4)completes the proof.

4 Some Examples

4.1 Some standard Korn inequalities

Proposition 4.1LetObe a Korn-Wirtinger domain.Letωbe a non-empty open subset ofOor an open subset of the boundary of a Lipschitz subdomain ofO.Then,there is a constantCsuch that

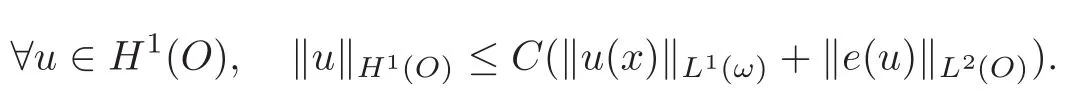
In particular,

then

Proof Set

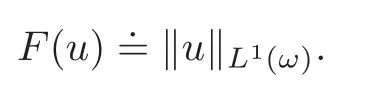
Clearly,F is Lipschitz on H1(O)by injection into L2(O)(resp.by a trace theorem into L2(ω))and F|Ris a semi-norm on R.Furthermore,F(r)=0 implies that r vanishes at every point of ω.Since ω is open(resp.is open in a Lipschitz surface),it contains at least three non-aligned points where r vanishes.One concludes that r vanishes everywhere in R3(one easy argument is to use the equi-projectivity of every rigid motion).

This Korn inequality applies for example when the vector field u satisfies a homogeneous or non-homogeneous Dirichlet condition on a non-empty open subset of the boundary∂O.

Remark 4.1The previous result can be extended to the case where the norm on ω is taken in L2(ω;µ)where µ is a non zero-measure offinite energy(i.e.,in the dual space of H1(O)).

4.2 Some non-standard Korn inequalities

This section starts with a trivial remark concerning rigid motions:Every rigid motion is divergence-free.

Proposition 4.2Letωbe a bounded open set with Lipschitz boundary inR3.Then theis a semi-norm onR.Its kernel consists of all the rigid motions whichare tangent to∂ω.

ProofBy the Stokes theorem applied in ω,and since divr=0,it follows thatR∂ωrνdσ =0.Consequently,

The conclusions follow.

We discuss now under which conditions this map is a norm on R.

Definition 4.1(Locked Domains)Letωbe a bounded open domain with Lipschitz boundary inR3.It is said to be locked if the mapr → ‖(rν)+‖L1(∂ω)is a norm onR.Because of(4.1),a domain is locked if and only if the only rigid motion tangent to its boundary is0.Making use of the exponential map one can see that a domain is locked if and only if its isometry group is discrete.

Consequently,the only domains which are not locked in R3are euclidean balls,zones between two concentric euclidean spheres(the isometry group is SO3),and domains of revolution around an axis(the isometry group is isomorphic to S1).For a domain ω,Rωwill denote the set of rigid motions which are tangent to∂ω.It is reduced to zero for locked domains.

Since the boundary of a domain ω can have several connected components,for ω to be locked,it is enough that one of these components not be of revolution.This component then locks the domain(e.g.,the complement of a small ball in a larger cube).It may also be that several components are needed to lock the domain(e.g.,the zone between two non intersecting spheres is not locked if the spheres are concentric,but is locked if they are not).

We now introduce notations for the classical moments of a vectorfield.

Definition 4.2(Moments)Letωbe a bounded open subset ofR3(resp.of a Lipschitz surface inR3).Letzbe a point inR3andda unit vector inR3.For a vectorfieldϕinL1(ω)its(vector)moment(ϕ)at the pointzand its(scalar)moment(ϕ)with respect to the axis with directiondgoing throughzare

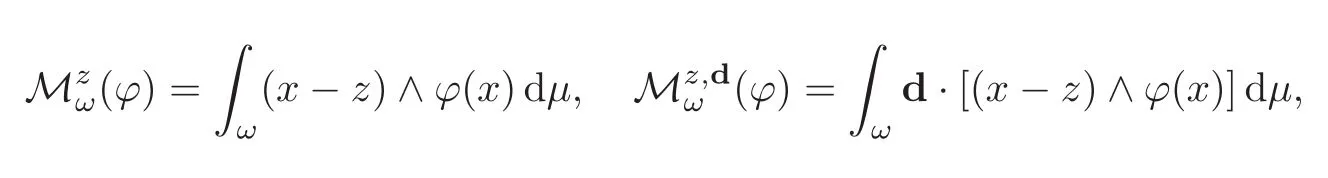
whereµis the Lebesgue measure onω (resp.the superficial measure onω).Whenzis the origin,it will be omitted in the notation of the moments.

These functions are clearly linear continuous on the space L1(ω),hence on the space H1(O)as soon as O contains ω as a subdomain(resp.when ω is an open subset of the boundary of a Lipschitz subdomain of O).

One can also use a measure different from the Lebesgue measure in ω (resp.the superficial measure on ω)provided it is also offinite energy(i.e.,in the dual space of H1(Ω))so that the moments are continuous on H1(O).In particular,one can use a density measure ρ(x)dx with ρ non-negative and in L2(O).

Note that if ω is an open subset of a sphere of center z and radius R,(ϕ)is bounded in norm by R‖ϕτ‖L1(ω)(recall that ϕτis the tangential component of ϕ),and if it is an open subset of a surface of revolution of radius R around the axis going through z with direction d,the absolute value of(ϕ)is bounded by R‖d∧ ϕτ‖L1(ω)(d ∧ ϕτis the podal component of ϕ).

Moments are a source of semi-norms on R.

Lemma 4.1(Norms and Semi-norms onR)

Locked domainsLetObe a locked domain andΣ(O)a union of connected components of∂Owhich locksO.Then,

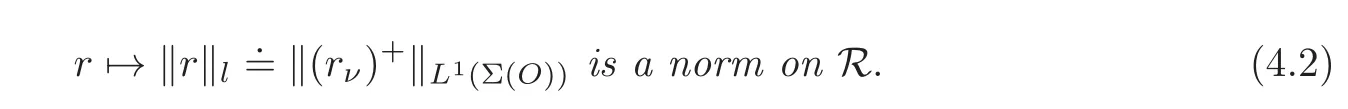
For non-locked domains this map is only a semi-norm onR.

Domains with spherical symmetryLetΣbe an euclidean sphere centered at the origin(i.e.,a connected component of the boundary of a domain with spherical symmetry with respect to the origin).Then,there is a constantCand a linear mapbfromRtoR3such that

Furthermore,ifωis a bounded open subset ofR3(resp.of a Lipschitz surface inR3),then

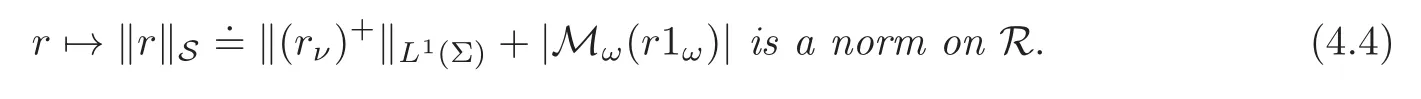
Domains of cylindrical revolutionLetObe an open domain of revolution around an axis going through the origin and with directiond.LetΣbe a Lipschitz connected component of its boundary.Then,there is a constantCand a linear mapℓfromRtoRsuch that

Furthermore,ifωis a bounded open subset ofR3(resp.of a Lipschitz surface inR3),then

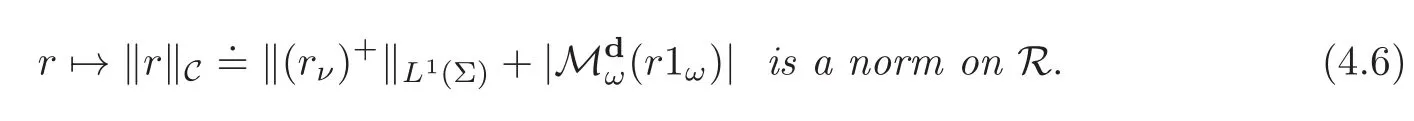
Proof Locked domainsFirst remark that every connected component of the boundary of(any domain)O is the boundary of a bounded domain(its “interior”).Therefore Proposition 4.2 applies for each component and ‖ ·‖lis a semi-norm on R.If‖r‖l=0,it implies that r|Σ(O)is tangent on every component of Σ(O).Since the latter is not globally of revolution,this implies that r=0,so that‖·‖lis a norm.

Domains with spherical symmetryLet Σ be a sphere centered at the origin.Here also,the map ‖ ·‖lis a semi-norm on R whose kernel consists of all the rigid motions which are tangent to Σ,namely RΣ{b∧Id|b∈ R3}.Therefore,it is a norm on an orthogonal of RΣin R(for this,any scalar product on thefinite dimensional space R will do),and b∧Id is simply the orthogonal projection on RΣ.

The map ‖ ·‖Sof formula(4.4)is also a semi norm.But if r is in its kernel,it is both tangent to Σ,hence of the form b ∧ Id and with vanishing moment on ω.This condition reads

hence

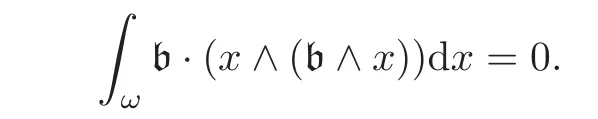
Now b·(x∧(b∧x))=|x|2|b|2−(b·x)2which is non-negative and can only vanish for x collinear with b if the latter is not zero.But this cannot hold for every x in ω(because it is of dimension at least 2).Therefore,b has to be 0 and the kernel is reduced to 0.

Domains with cylindrical symmetryThe reasoning is the same here.The elements of ROare the rigid motions of the form{kd∧Id|k∈R}.Imposing further that the moment with respect to d at the origin vanish reads

but,as above,the last integral vanishing implies d=0.

The maps ‖·‖l,‖ ·‖Sand ‖·‖Cextends in the obvious way(and with the same notations)to the space H1(O)as Lipschitz functions,leading to simple corollaries of Theorem 3.1 which give some unilateral Korn inequalities.

Corollary 4.1LetObe a Korn-Wirtinger domain which is locked by a subsetΣof its boundary.Letνbe a choice of unit normal toΣ.Then,there exists a constantCsuch that the following generalized Korn inequality holds3Since there are 2kchoices of ν (where k is the number of distinct connected components making up Σ)there are as many distinct inequalities!:

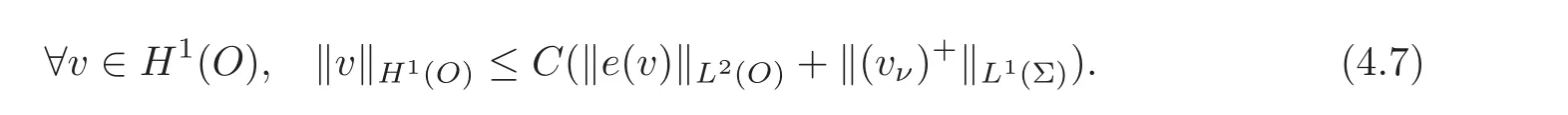
Corollary 4.2LetObe a Korn-Wirtinger domain andΣa spherical connected component of its boundary(for simplicity,centered at the origin).Then,there exists a constantCand a continuous linear mapb:H1(O)→R3such that

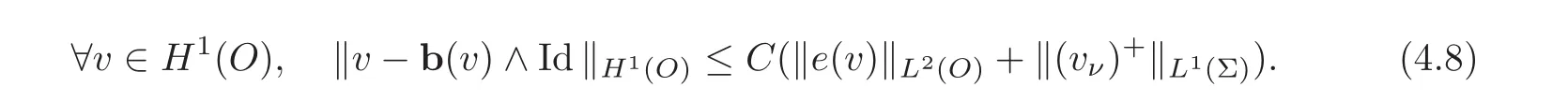
Moreover,ifωis a bounded open subset ofO(resp.of the boundary of a Lipschitz subdomain ofO),then there exists a constantC′such that

Corollary 4.3LetObe a Korn-Wirtinger domain andΣa connected component of its boundary invariant under the rotations around the axis with unit vectord(for simplicity,through the origin).Then,there exists a constantCand a continuous linear mapℓ:H1(O)→ Rsuch that

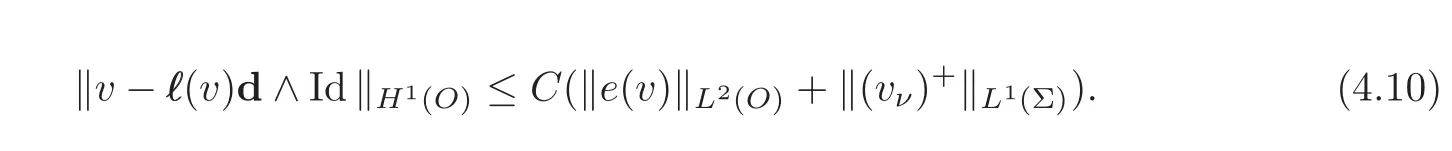
Moreover,ifωis a bounded open subset ofO(resp.of a Lipschitz surface in,then there exists a constantC′such that

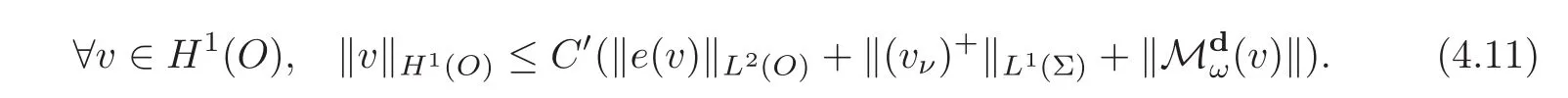
Proof of Corollary 4.1Theorem 3.1 applies with F(u)‖u‖lwhich is Lipschitz continuous on H1(O).

Proof of Corollary 4.2The second part follows in the same way as above from the fact that the map F(u)‖u‖Sextends the map defined in(4.4)and is Lipschitz continuous on H1(O).

The proof of the first part goes as follows.Given u in H1(O)and using the definition of a Korn-Wirtinger domain,there is a r(u)in R with inequality(2.4).Applying the map b given in(4.3)to r(u)then gives(recall that all norms are equivalent on R)

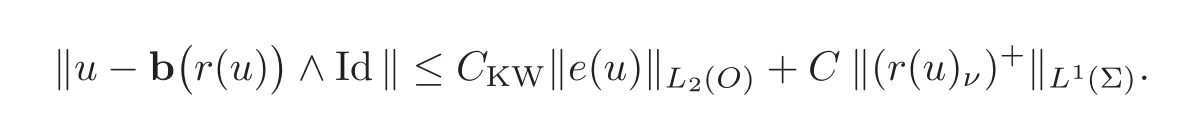
From(2.4)again,and using the trace theorem on Σ,

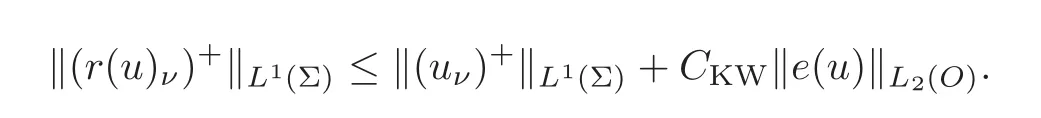
Combining these two inequalities gives inequality(4.8).

The proof of Corollary 4.3 is similar.

AcknowledgementThe author expresses his thanks to the(anonymous)referee who found many typos and made several suggestions to improve the manuscript.

[1]Ciarlet,P.and Ciarlet,P.G.,Another approach to linearized elasticity and a new proof of Korn’s inequality,Mathematical Models and Methods in Applied Sciences,15(2),2005,259–271.

[2]Cioranescu,D.,Damlamian,A.and Orlik,J.,Homogenization via unfolding in periodic elasticity with contact on closed and open cracks,Asymptotic Analysis,82,2013,201–232.

[3]Damlamian,A.,Some unilateral Korn inequalities with application to a contact problem with inclusions,C.R.Acad.Sci.Paris,Ser.I,350,2012,861–865.

[4]Eck,C.,Jaruˇsek,J.and Krbec,M.,Unilateral Contact Problems:Variational Methods and Existence Theorems,CRC Press,Boca Raton,2005.

[5]Fichera,G.,Sul problema elastostatico di Signorini con ambigue condizioni al contorno,Atti Accad.Naz.Lincei Rend.Cl.Sci.Fis.Mat.Natur.,34(8),1963,138–142(in Italian).

[6]Fichera,G.,Problemi elastostatici con vincoli unilaterali:Il problema di Signorini con ambigue condizioni al contorno,Atti Accad.Naz.Lincei Mem.Cl.Sci.Fis.Mat.Natur.Sez.I,7(8),1963/1964,91–140(in Italian).

[7]Fichera,G.,Elastostatics problems with unilateral constraints,S´eminaire Jean Leray,3,1966–1967,64–68,http://www.numdam.org/item?id=SJL 1966-1967 3 64 0.

[8]Fichera,G.,Unilateral constraints in elasticity,Actes,Congr`es Intern.Math.Nice,3,1970,p.7.

[9]Gobert,J.,Une in´egalit´e fondamentale de la th´eorie de l’´elasticit´e,Bull.Soc.Roy.Sci.Li`ege,31,1962,182–191.

[10]Griso,G.,Decompositions of displacements of thin structures,J.Math.Pures Appl.,89,2008,199–223.

[11]Hlav´aˇcek,I.,Haslinger,J.,Neˇcas J.and Lov´ıˇcek,J.,Solution of Variational Inequalities in Mechanics,Springer-Verlag,New York,Berlin,Heidelberg,London Paris,Tokyo,1988.

[12]Kikuchi,N.and Oden,J.T.,Contact problems in elasticity,SIAM Studies in Applied Mathematics,SIAM,Philadelphia,1988.

[13]Oleinik,O.A.,Shamaev,A.S.and Yosifian,G.A.,Mathematical Problems in Elasticity and Homogenization,North-Holland,Amsterdam,1992.