Exact Boundary Synchronization for a Coupled System of Wave Equations with Neumann Boundary Controls∗

Tatsien LIXing LUBopeng RAO

(Dedicated to Philippe G.Ciarlet on the occasion of his 80th birthday)

1 Introduction

Synchronization is a widespread natural phenomenon.It wasfirst observed by Huygens in 1665(see[3]).The theoretical research on synchronization phenomenon from the mathematical point of view dates back to Wiener in 1950s(see[13]).However,almost all the previous works focused on systems described by ODEs,and studied the asymptotic synchronization of the states of the system as t→+∞.For coupled systems governed by PDEs,as shown by Li and Rao,synchronization can be realized in a limited time period by means of proper boundary controls,and after switching offall the controls,the state of synchronization remains.Precisely speaking,Li and Rao considered the exact boundary synchronization for a coupled system of wave equations with Dirichlet boundary controls in any given space dimensions in the framework of weak solutions(see[4,6]),and acquired related results for the same system in one space dimension with all kinds of boundary controls in the framework of classical solutions(see[2,9]).Moreover,they got also corresponding results on the exact boundary synchronization by groups in[5,7].

In this paper,we consider the following coupled system of wave equations with Neumann boundary controls:

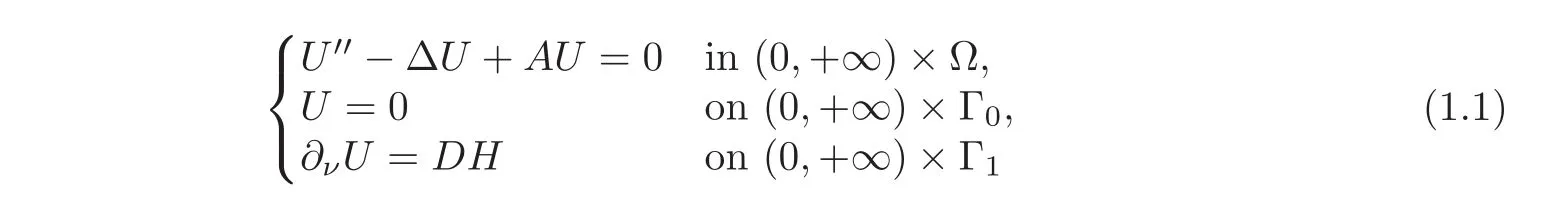
and the corresponding initial data

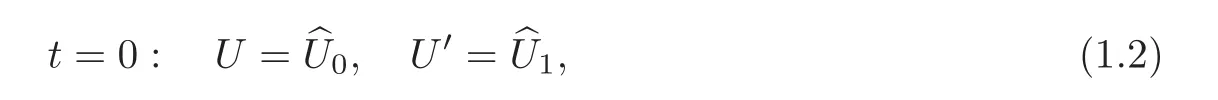
where Ω ⊂ Rnis a bounded domain with smooth boundary Γ =and mes(Γ0) ＞ 0,∂νdenotes the outward normal derivative on the boundary,the coupling matrix A=(aij)is of order N,the boundary control matrix D is a full column-rank matrix of order N ×M(M ≤ N),both A and D have real constant elements,U=(u(1),···,u(N))Tand H=(h(1),···,h(M))Tdenote the state variables and the boundary controls,respectively.

Denote

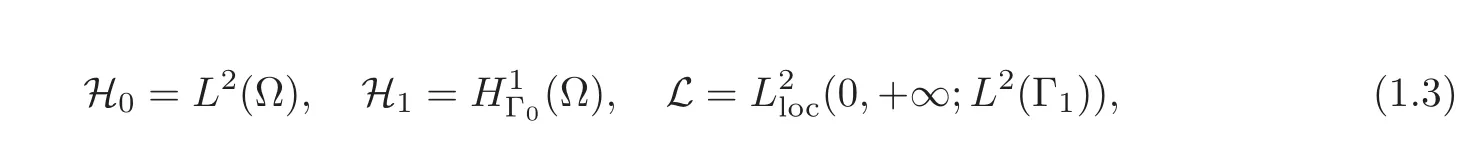
We assume that Ω satisfies the usual multiplier geometric control condition(see[1]).Without loss of generality,we assume that there exists an x0∈Rn,such that setting m=x−x0,we have

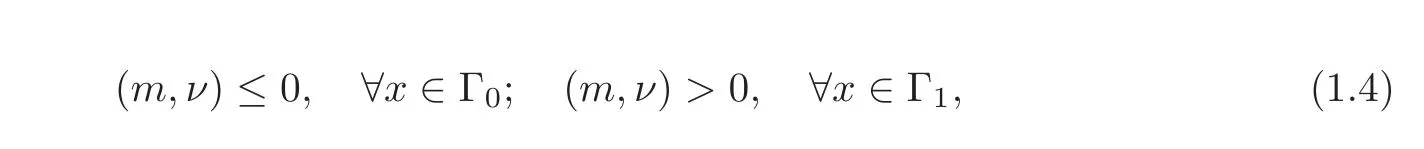
where(·,·)denotes the inner product in Rn.

Define the linear unbounded operator−Δ in H0by

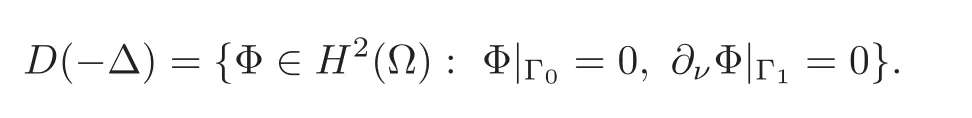
Clearly,−Δ is a positively definite self-adjoint operator with a compact resolvent.Then,for any given s∈ R,we can define the operatorwith the domaincontrolH∈LMwith compact support in[0,T],such that the corresponding mixed initialboundary value problem(1.1)–(1.2)admits a unique weak solutionU ∈ (Cloc([0,+∞);H1−s))N∩satisfying

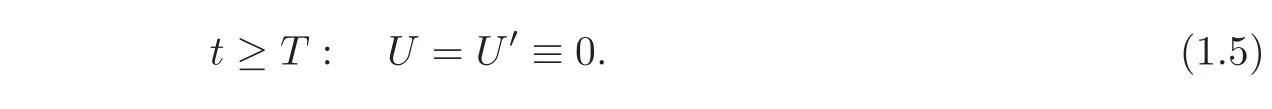
Moreover,we have the continuous dependence:

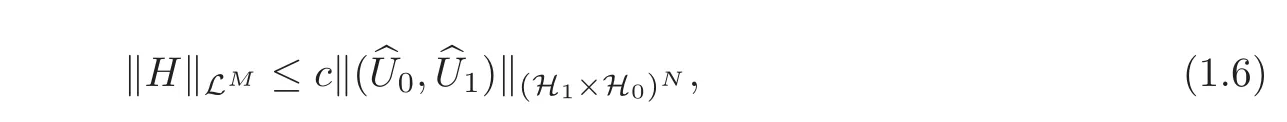
wherecis a positive constant.

For the exact boundary null controllability and the non-exact boundary null controllability of system(1.1),the following results were proved in[8].

Lemma 1.2WhenM=N,there exists a constantT＞0,such that system(1.1)is exactlynull controllable at the timeTfor any given initial data

However,if there is a lack of boundary controls,we have the following lemma.

Lemma 1.3WhenM＜N,no matter how largeT＞0is,system(1.1)is not exactly nullcontrollable at the timeTfor any given initial data

Therefore,it is necessary to discuss whether system(1.1)is controllable in some weaker senses when there is a lack of boundary controls,namely,when M＜N.Although the results are similar to those for the coupled system of wave equations with Dirichlet boundary controls,since the solution to a coupled system of wave equations with Neumann boundary conditions has a relatively weaker regularity,in order to realize the desired result,we need stronger function spaces,and the corresponding adjoint problem is also different.

Wefirst give the following lemma(see[10]).

Lemma 1.4For any givenN×NmatrixAand any given full row-rank(N−p)×NmatrixCwith1≤p＜N,the following properties are equivalent:

(1)Ker(C)is an invariant subspace ofA:

(2)There exists a unique matrixof order(N−p),such that

Moreover,the matrixis given by

whereC+denotes the Moore-Penrose inverse ofC:

Since Lemma 2.1 in[7]is independent of the type of boundary conditions,we still have the following lemma.

Lemma 1.5Assume thatUis the solution to the mixed problem(1.1)–(1.2).LetCbe a full row-rank(N−p)×Nmatrix(where1≤p＜N)such that

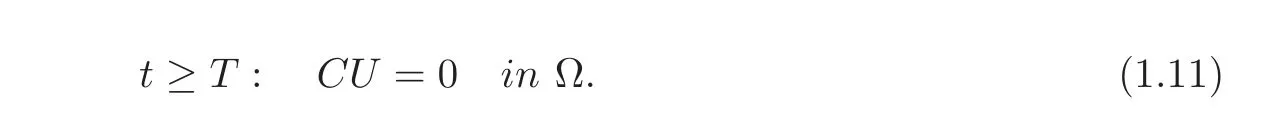
Then we have either

or there exists a full row-rank(N−p+1)×Nmatrix^Csuch that

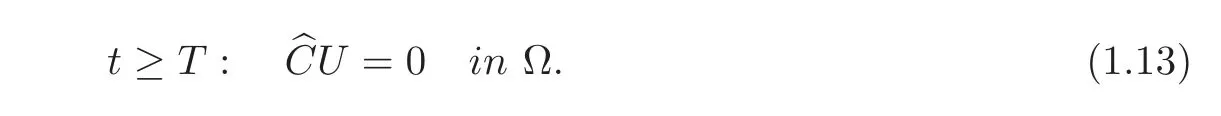
2 Exact Boundary Synchronization

Definition 2.1System(1.1)is exactly synchronizable at the timeT ＞ 0in the space(H1×H0)N,if for any given initial data(U0,U1)∈(H1×H0)N,there exists a boundary controlH∈LMwith compact support in[0,T],such that the weak solutionU=U(t,x)to the mixed initial-boundary value problem(1.1)–(1.2)satisfies

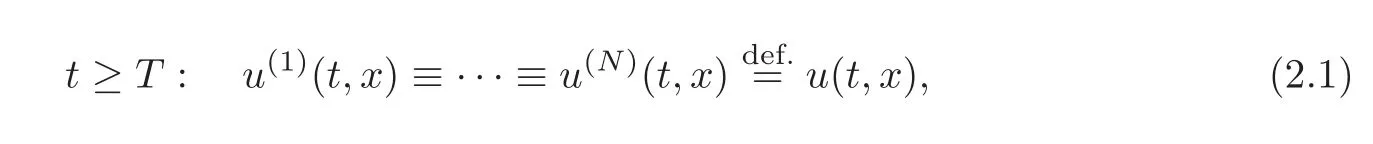
where,u=u(t,x),being unknown a priori,is called the corresponding state of synchronization.

The above definition requires that system(1.1)maintains the state of synchronization even though the boundary control is canceled after the time T.

Theorem 2.1Assume thatM＜N.If system(1.1)is exactly synchronizable in the space(H1×H0)N,then the coupling matrixA=(aij)should satisfy the following condition of compatibility(the sums of elements in every row are equal to each other):

whereais a constant independent ofi=1,···,N.

ProofBy Lemma 1.3,since M＜N,system(1.1)is not exactly null controllable,then there exists an initial data(U0,U1)∈(H1×H0)N,such that for any given boundary control H,the corresponding state of synchronization u(t,x)/≡0.Then,noting(2.1),the solution to problem(1.1)corresponding to this initial data satisfies

for all i=1,···,N.Then we have

for i,k=1,···,N.It follows that

which is just the required condition of compatibility(2.2).

Now,let

be the corresponding matrix of synchronization.C1is a full row-rank matrix,and Ker(C1)=Span{e1},where e1=(1,1,···,1)T.Clearly,the synchronization(2.1)can be equivalently written as

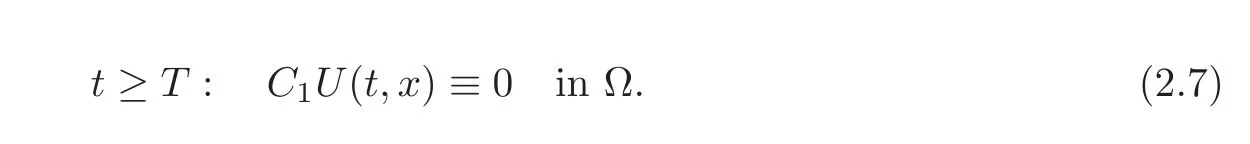
By Lemma 1.4,we have

Lemma 2.1The following properties are equivalent:

(1)The condition of compatibility(2.2)holds;

(2)e=(1,1,···,1)Tis a right eigenvector ofA,corresponding to the eigenvalueagiven by(2.2);

(3)Ker(C1)is a one-dimensional invariant subspace ofA:

(4)There exists a unique matrixof order(N−1),such that

A1=is called the reduced matrix ofAbyC1,where

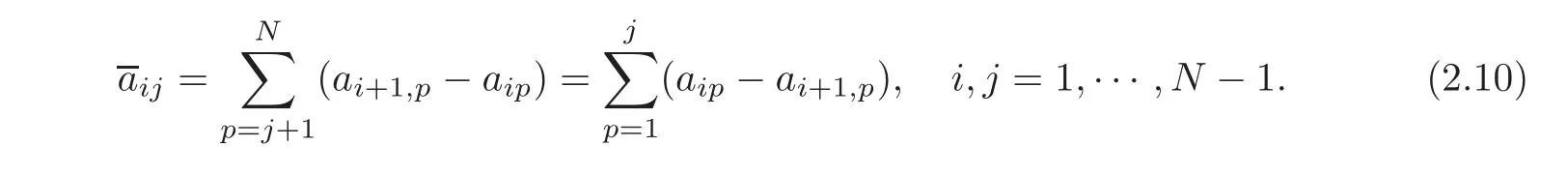
Theorem 2.2Assume thatM=N−1.Under the condition of compatibility(2.2),if the matrixC1Dis invertible,namely,rank(C1D)=N−1,then there exists a constantT＞0so large that system(1.1)is exactly synchronizable at the timeTin the space(H1×H0)N,moreover,we have the continuous dependence:

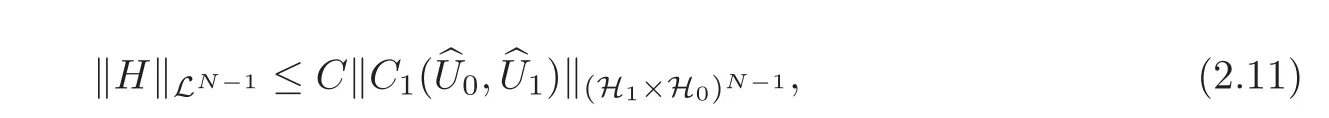
whereCis a positive constant.

On the other hand,whenrank(C1D)＜N−1(especially,whenM＜N−1),no matter how largeT＞0is,system(1.1)is not exactly synchronizable at the timeT.

ProofUnder the condition of compatibility(2.2),let

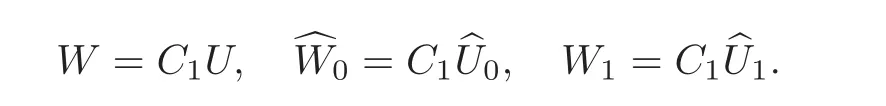
Noting(2.9),it is easy to see that the original mixed problem(1.1)—(1.2)for U can be reduced to the following self-closed mixed problem for W:

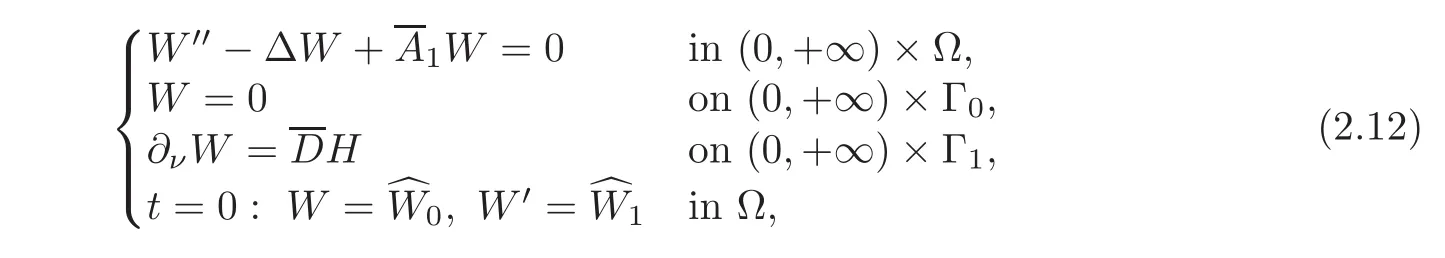
where D=C1D.Noting that C1is a surjection from(H1×H0)Nonto(H1×H0)N−1,we easily check that the exact boundary synchronization of system(1.1)for U is equivalent to the exact boundary null controllability of system(2.12)for W.Since rank=rank(C1D)=N−1,by Lemma 1.2,for any given initial data(,∈ (H1×H0)N−1,system(2.12)is exactly null controllable by means of a boundary controlH ∈ LN−1.By(1.6)in Definition 1.1,we get the continuous dependence(2.11).Sinceis invertible matrix,there exists a corresponding boundary control H ∈LN−1,such that system(1.1)is exactly synchronizable.

On the other hand,when rank(C1D)＜N−1,H can be rewritten assuch thatis a full column-rank matrix of order N×with＜N−1 and∈L~Mwith compact support in[0,T],by Lemma 1.3,the reduced system(2.12)is not exactly null controllable,then system(1.1)is not exactly synchronizable either.

3 Exact Boundary Synchronization by p-Groups

When there is a further lack of boundary controls,we consider the exact boundary synchronization by p-groups(p≥1;when p=1,it becomes the exact boundary synchronization).This indicates that the components of U are divided into p groups:

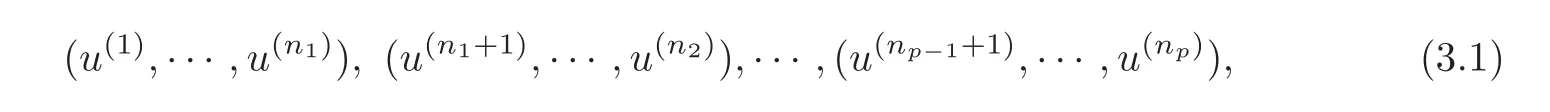
where 0=n0＜ n1＜ n2＜ ···＜ np=N,and each group is required to possess the exact boundary synchronization,respectively.

Definition 3.1System(1.1)is exactly synchronizable byp-groups at the timeT ＞ 0in the space(H1×H0)N,if for any given initial data()∈(H1×H0)N,there exists a boundary controlH∈LMwith compact support in[0,T],such that the weak solutionU=U(t,x)to the mixed initial-boundary value problem(1.1)–(1.2)satisfies

where,(u1,···,up)T,being unknown a priori,is called the corresponding state of synchronization byp-groups.

and let Cpbe the following(N−p)×N matrix of synchronization by p-groups:

Obviously,we have

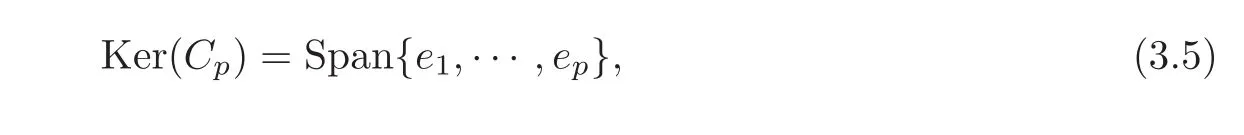
where for 1≤s≤p,

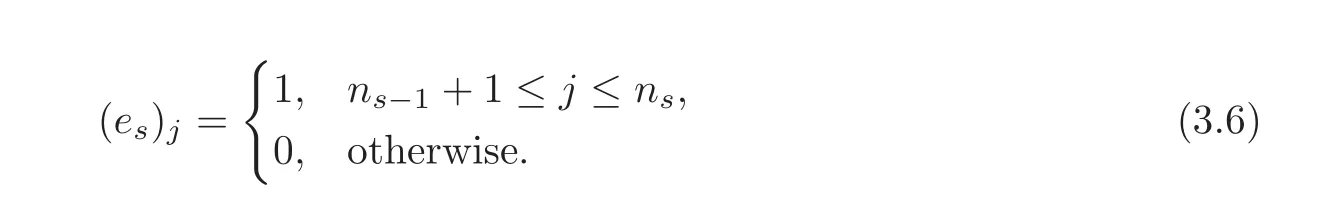
Thus,(3.2)can be equivalently written as

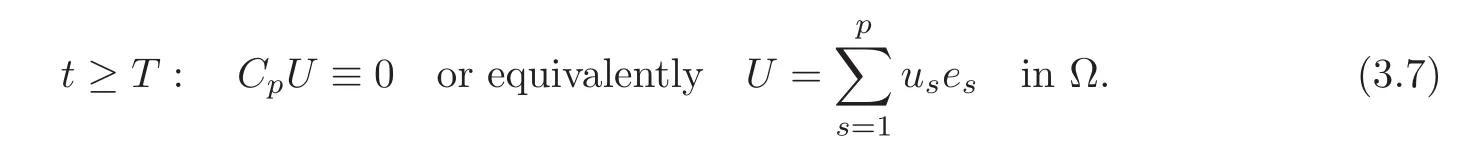
Theorem 3.1Assume that system(1.1)is exactly synchronizable byp-groups.Then we necessarily haveM≥N−p.Especially,whenM=N−p,the coupling matrixA=(aij)should satisfy the following condition of compatibility:

is a surjection from(H1×H0)Nonto(H1×H0)N−p+r,then,(3.11)is exactly null controllable at the time T in the space(H1×H0)N−p+r.By Lemmas 1.2—1.3(cf.the last paragraph in the proof of Theorem 2.2),we necessarily have

then

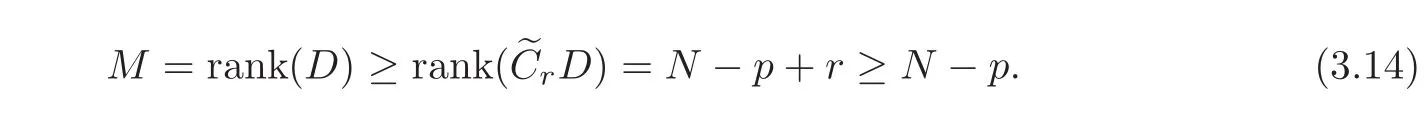
In particular,when M=N−p,we have r=0,namely,the condition of compatibility(3.8)holds.

Remark 3.1The condition of compatibility(3.8)is equivalent to the fact that there exist some constants αrs(1 ≤ r,s≤ p)such that

or,noting(3.6),A satisfies the following row-sum condition by blocks:

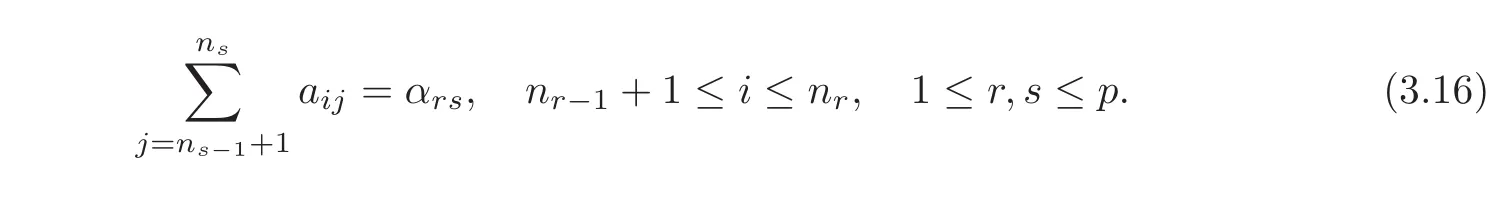
Especially,this condition of compatibility becomes(2.2)when p=1.

Theorem 3.2LetCpbe the(N −p)×Nmatrix of synchronization byp-groups defined by(3.3)–(3.4).Under the condition of compatibility(3.8),assume that theN ×(N −p)boundary control matrixDhas full column-rank and satisfiesrank(CpD)=N − p.Then system(1.1)is exactly synchronizable byp-groups by means of boundary controlH ∈LN−p,moreover,we have the continuous dependence:

whereCis a positive constant.

On the other hand,whenrank(CpD)＜N−p(especially,whenM＜N−p),no matter how largeT＞0is,system(1.1)is not exactly synchronizable byp-groups at the timeT.

ProofAssume that the coupling matrix A=(aij)satisfies the condition of compatibility(3.8).By Lemma 1.4,there exists a unique matrixof order(N−p),such that

Setting

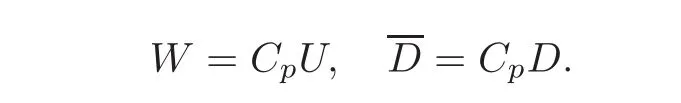
We can similarly get the following reduced system for W:

where W is a vector valued function of(N−p)components.By the assumption that rank(D)=rank(CpD)=N−p and Lemma 1.2,system(3.19)is exactly null controllable.Also,by(1.6)in Definition 1.1,we get the continuous dependence(3.17).Then the original system(1.1)for U is exactly synchronizable by p-groups.

On the other hand,when rank(CpD)＜N−p,by Lemma 1.3(cf.the last paragraph in the proof of Theorem 2.2),the reduced system(2.12)is not exactly null controllable,then system(1.1)is not exactly synchronizable by p-groups.

4 Determination of the State of Synchronization by p-Groups

Now,under the condition of compatibility(3.8),we are going to discuss the determination of the state of synchronization by p-groups for system(1.1).Generally speaking,the state of synchronization should depend on the initial data()and the applied boundary control H.However,when the coupling matrix A possesses some good properties,the state of synchronization by p-groups is independent of the applied boundary control,and can be determined entirely by the solution to a system of wave equations with homogeneous boundary condition.

First,by Lemma 1.1 and noting that the space(H1× H0)Ngiven in Definition 3.1 is included in(H1−s× H−s)N?s ＞）,differently from the case of Dirichlet boundary controls,the attainable set of states of exact boundary synchronization by p-groups for the system with Neumann boundary controls is not the whole space(H1−s× H−s)p.Besides,as in the case of Dirichlet boundary controls(see[6]),the choice of boundary controls is not unique.We have the following theorem.

Theorem 4.1LetHdenote the set of all the boundary controlsHwhich can realize the exact boundary synchronization byp-groups at the timeTfor system(1.1).If the condition of compatibility(3.8)holds,then forε＞ 0small enough,the value ofH ∈ Hon(0,ε)×Γ1can be arbitrarily chosen.

ProofFirst of all,there exists a T0＞0 independent of the initial data,such that,when T＞T0,the reduced problem(3.19)is exactly null controllable at the time T.According to the proof of Theorem 3.2,the exact synchronization by p-groups of system(1.1)is equivalent to the exact null controllability of the reduced system(3.19).Therefore,taking an ε＞ 0 so small that T−ε＞T0,system(1.1)is still exactly synchronizable by p-groups at the time T−ε.

we solve the forward problem(1.1)on the time interval[0,ε]with H=and get the solutionas initial data,by

Theorem 3.2,for system(1.1)we canfind a boundary control

such that the corresponding solutionsatisfies exactly the initial condition

and realizes the synchronization by p-groups at the time t=T.Let

It can be verified that U is the solution to the mixed problem(1.1)with boundary control H,and it is exactly synchronizable by p-groups at the time T.By this way,we get an infinity of boundary controls H,the values of which on(0,ε)× Γ1can be taken arbitrarily.Finally,by the denseness of(Ω)in H1and H0,we can get the desired result.

The state of synchronization by p-groups is closely related to the properties of the coupling matrix A.Let

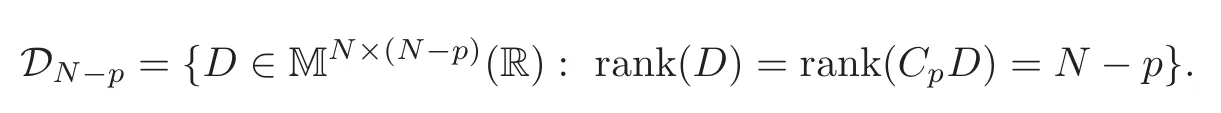
By[7],D ∈DN−pif and only if it can be expressed by

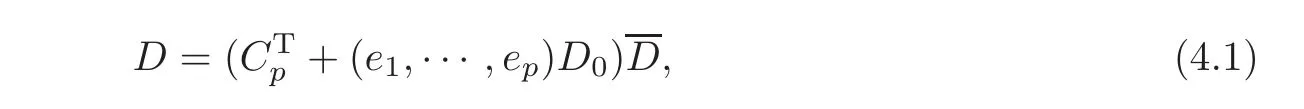
where D0is a p×(N−p)matrix,andis a reversible matrix of order(N−p).We have the following theorem.

Theorem 4.2Under the condition of compatibility(3.8),assume thatATpossesses an invariant subspaceSpan{E1,E2,···,Ep}which is bi-orthonormal toKer(Cp)=Span{e1,···,ep}:

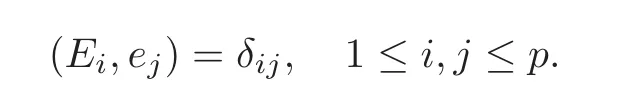
Then there exists a boundary control matrixD∈DN−p,such that the state of synchronization byp-groupsu=(u1,···,up)Tis independent of the applied boundary controls,and can be determined as follows:

whereψ =(ψ1,···,ψp)Tis the solution to the following problem with homogeneous boundary condition:

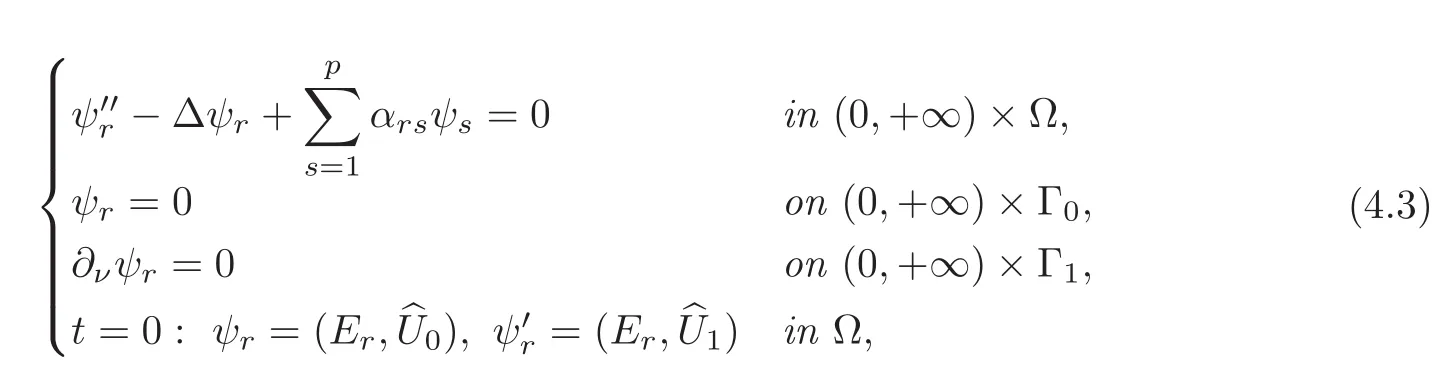
whereαrs(1 ≤ r,s≤ p)are given by(3.16).

ProofNoting that Span{E1,E2,···,Ep}is bi-orthonormal to Ker(Cp)=Span{e1,···,ep},and taking

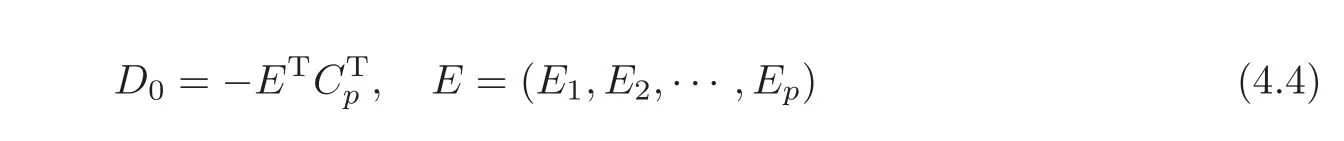
in(4.1),we get a boundary control matrix D∈DN−p,such that

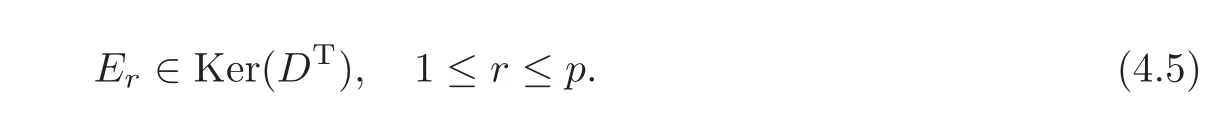
On the other hand,since Span{E1,E2,···,Ep}is an invariant subspace of AT,we may denote

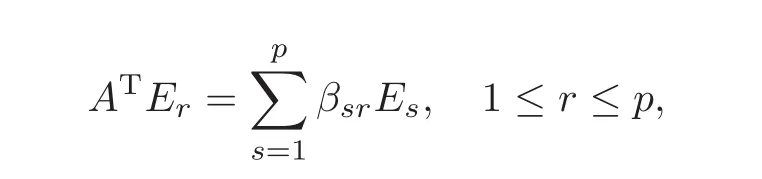
where βsrare some constants.By

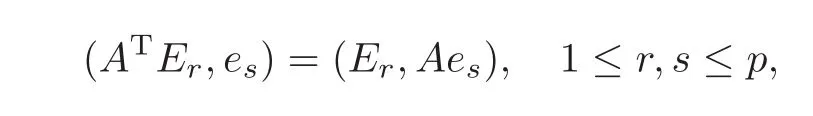
and noticing(3.15),we have

Then by bi-orthonormality,we get

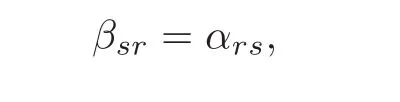
namely,

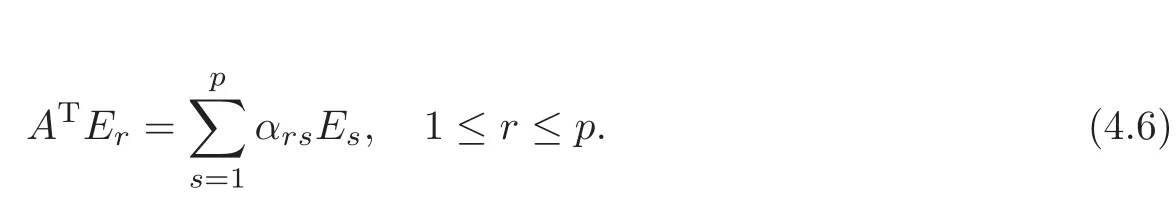
Let ψr=(Er,U).Taking the inner product with Eron both sides of(1.1),we get(4.3).Finally,for the state of synchronization by p-groups,by(3.7)we have

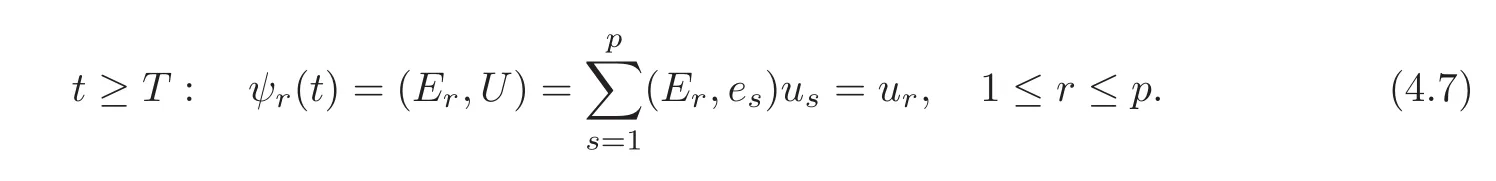
When ATdoes not possess any invariant subspace Span{E1,E2,···,Ep}which is biorthonormal to Ker(Cp)=Span{e1,···,ep},we can use the solution of(4.3)to give an estimate on the state of synchronization by p-groups.

Theorem 4.3Under the condition of compatibility(3.8),assume that there exists a subspaceSpan{E1,E2,···,Ep}that is bi-orthonormal toSpan{e1,···,ep}.Then there exist a boundary control matrixD∈DN−pand a constantcindependent of the initial data,such that the state of synchronization byp-groupsu=(u1,···,up)Tsatisfies the following estimate:

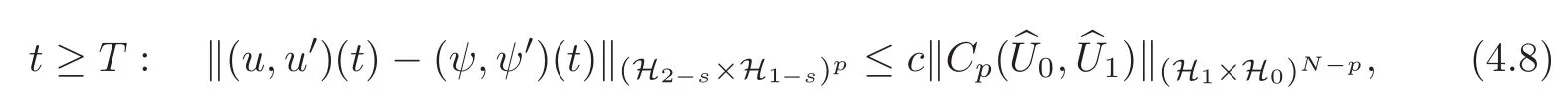
whereψ =(ψ1,···,ψp)Tis the solution to problem(4.3),ands ＞

ProofSince{E1,E2,···,Ep}is bi-orthonormal to{e1,···,ep},similar to(4.4),there exists a boundary control matrix D ∈ DN−p,such that(4.5)holds.Let φr=(Er,U).Taking the inner product with Eron both sides of(1.1)—(1.2),we get

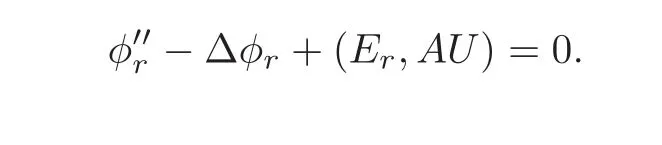
Since

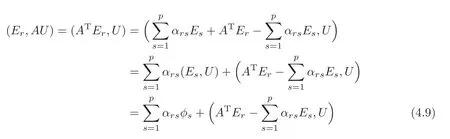
and for any given k ∈ {1,···,p},we have

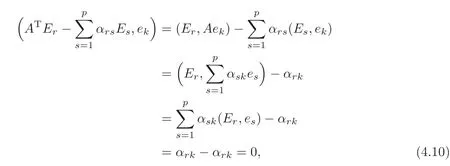
we get

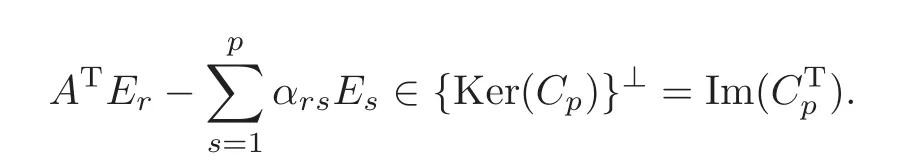
Therefore,there exists a vector Rr∈ RN−p,such that

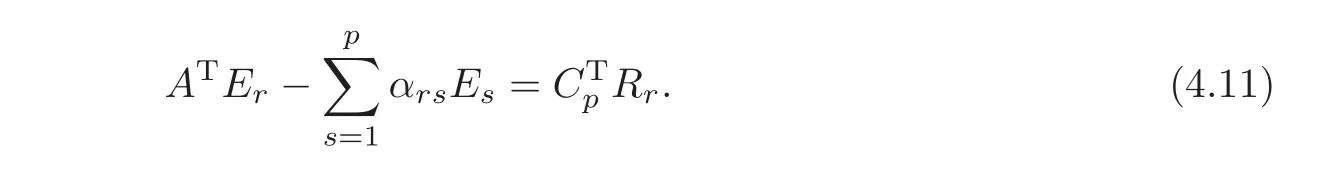
Thus,for r=1,···,p,we have

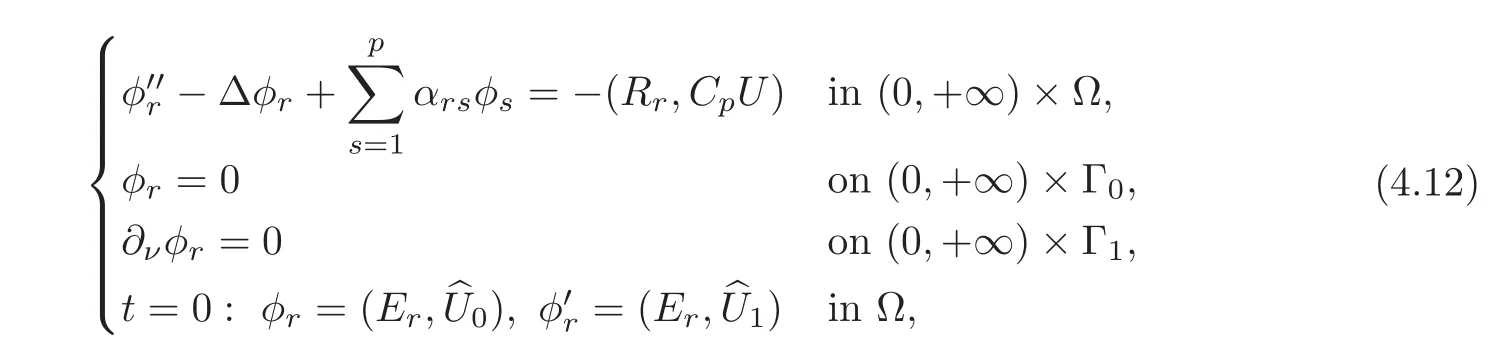
where αrs(1 ≤ r,s ≤ p)are defined by(3.16),and U=U(t,x) ∈ C(0,T;(H1−s)N)∩C1(0,T;(H−s)N)is the solution to the mixed initial-boundary value problem(1.1)—(1.2).Moreover,we have

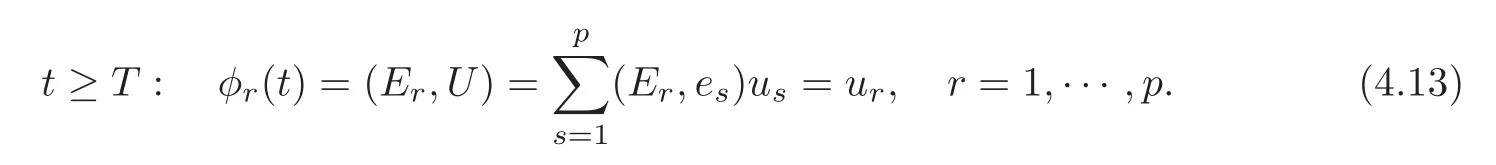
Noting that(4.3)and(4.12)possess the same initial data and the same boundary condition,by the well-posedness for a system of wave equations with Neumann boundary condition,we have(see[12,Chapter III])that,when t≥0,

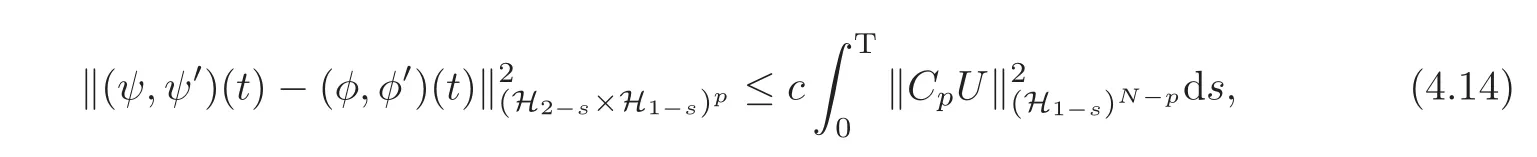
where,c is a positive constant.Noting that W=CpU,by well-posedness of the reduced problem(3.19)(see[12,Lemma 1.1]),we have

Moreover,by(3.17)we have

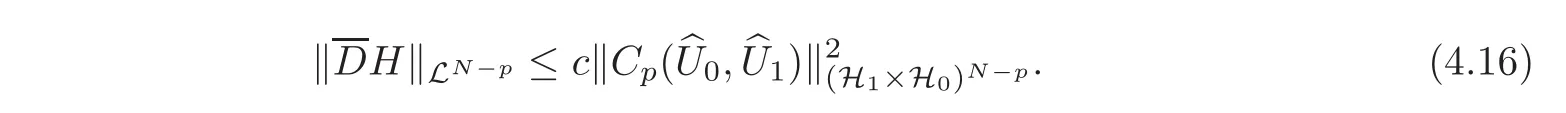
Substituting it into(4.15),we have

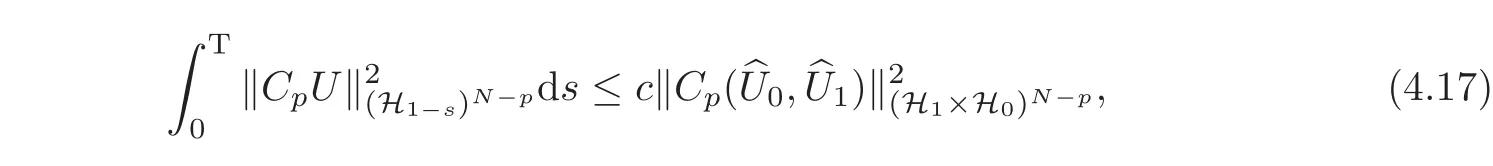
then,by(4.14)we get

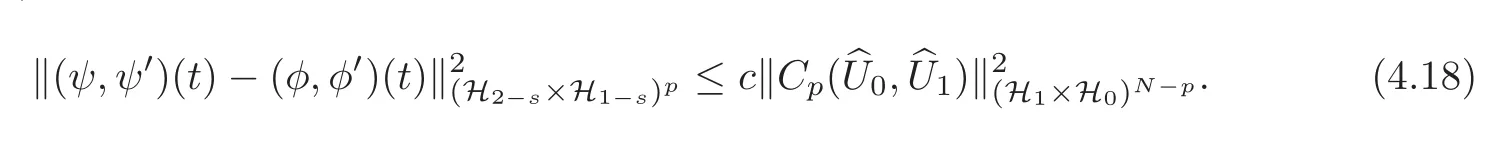
Substituting(4.13)into(4.18),we get(4.8).

Remark 4.1Differently from the case of Dirichlet boundary controls,although the solution to the problem(1.1)with Neumann boundary controls possesses a weaker regularity,the solution to the problem(4.3),which determines the state of synchronization by p-groups,possesses a higher regularity than the original problem(1.1)itself,then,this improved regularity makes it possible to approach the state of synchronization by p-groups by a solution to a relatively smoother problem.

In order to exactly express the state of synchronization by p-groups,we can extend the subspace Span{e1,···,ep}to an invariant subspace Span{e1,···,ep,···,eq}of A,such that ATpossesses an invariant subspace Span{E1,···,Ep,···,Eq},which is bi-orthonormal to Span{e1,···,ep,···,eq}.

Let

in which the tensor product is defined by

P can be represented by a matrix of order N.It is easy to see that

and

Let U=U(t,x)be the solution to the mixed initial-boundary value problem(1.1)—(1.2).We define its synchronizable part Usand controllable part Uc,respectively,as follows:

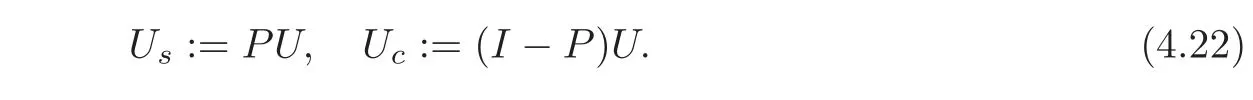
If system(1.1)is exactly synchronizable by p-groups,then

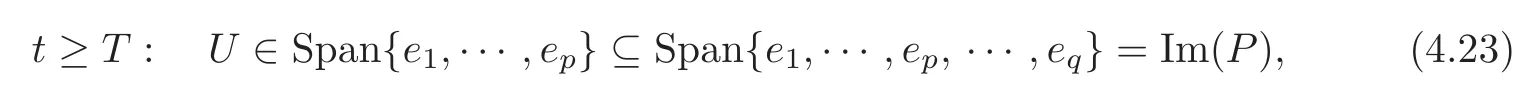
hence we have

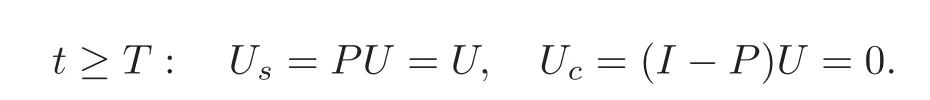
Noting(4.21),multiplying P and(I−P)from the left on both sides of(1.1)respectively,we see that the synchronizable part Usof U satisfies the following system:

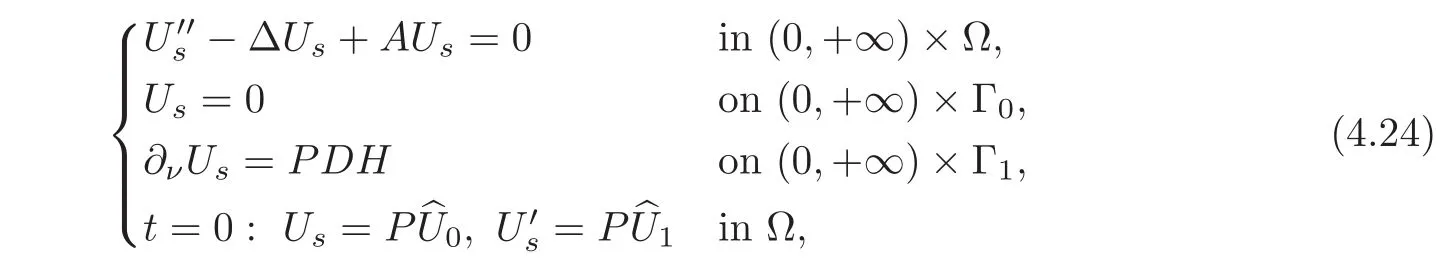
while,the controllable part Ucof U satisfies the following system:

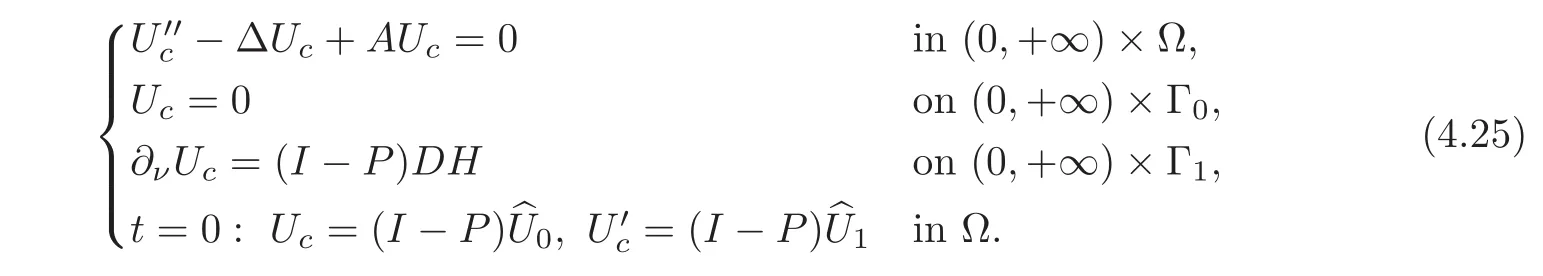
In fact,under the boundary control H,Ucwith the initial data((I−P)∈ Ker(P)×Ker(P)is exactly null controllable,while,Uswith the initial data∈ Im(P)×Im(P)is exactly synchronizable.

Theorem 4.4Assume that the condition of compatibility(3.8)holds.LetPbe defined by(4.19).If system(1.1)is exactly synchronizable byp-groups,and the synchronizable partUsis independent of the applied boundary controlHfort≥T,then we have

In particular,ifnull controllable.

ProofBy Theorem 4.1,the value of H on(0,ε)× Γ1can be arbitrarily taken.If the synchronizable part Usis independent of the applied boundary control H for t≥T,then we have

hence

Noting(4.20),we have

then p=q.

5 Determination of the State of Exact Boundary Synchronization

In the case of exact boundary synchronization,by Lemma 2.1,(1,1,···,1)Tis a right eigenvector of A,corresponding to the eigenvalue a defined by(2.2).Let ε1,ε2,···,εrand E1,E2,···,Erwith r ≥ 1 be the Jordan chains of A and AT,respectively,corresponding to the eigenvalue a,and Span{ε1,ε2,···,εr}is bi-orthonormal to Span{E1,E2,···,Er}.Thus we have

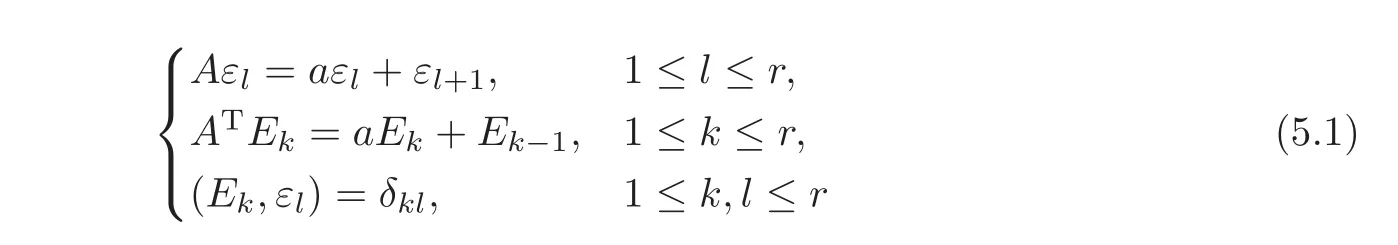
with

Let U=U(t,x)be the solution to the mixed initial-boundary value problem(1.1)—(1.2).If system(1.1)is exactly synchronizable,then

where u=u(t,x)is the corresponding state of synchronization.The synchronizable part and the controllable part are,respectively,

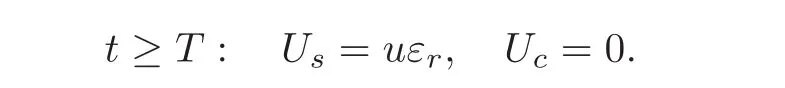
If the synchronizable part is independent of the applied boundary control H,by Theorem 4.4,we have r=1,then A possesses a left eigenvector E1such that

Generally speaking,when r≥1,setting

noting(4.19)and(4.22),we have

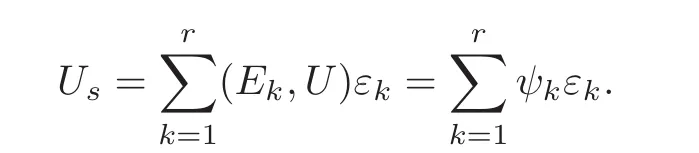
Thus,(ψ1,···,ψr)are the coordinates of Usunder the basis(ε1,ε2,···,εr).

Taking the inner product with Ekon both sides of(4.24),we get the following theorem.

Theorem 5.1Letε1,ε2,···,εrandE1,E2,···,Erbe the Jordan chains ofAandAT,respectively,corresponding to the eigenvaluea,in whichεr=(1,···,1)T.Then the synchronizable partUs=(ψ1,···,ψr)is determined by the following system(1 ≤ k ≤ r):

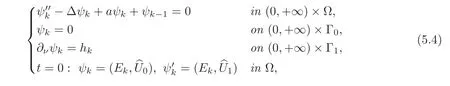
where

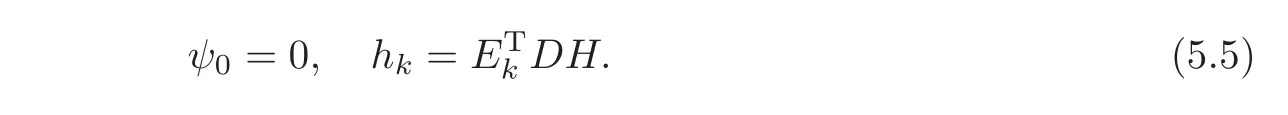
Noting(5.3),we have

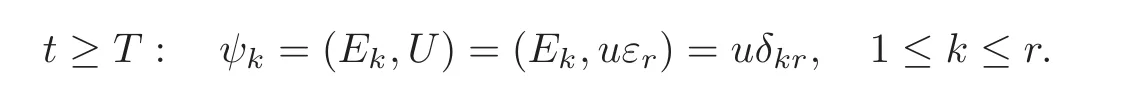
Thus,the state of synchronization u is determined by

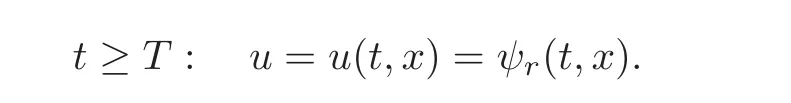
However,in order to get the state of synchronization u,we must solve the whole coupled problem(5.4)—(5.5).

6 Determination of the State of Exact Boundary Synchronization by 3-Groups

In this section,for an example,we will give the details on the determination of the state of exact boundary synchronization by 3-groups for system(1.1).The state of synchronization by pgroups can be discussed in a similar way.We always assume that the condition of compatibility(3.8)is satisfied.

By synchronization by 2-groups,when t≥T,we have

Recall that the matrix C3of synchronization by 3-groups is defined by(3.4).Let

Obviously,we have that

and that the state of synchronization by 3-groups is given by(6.1)—(6.3)means that

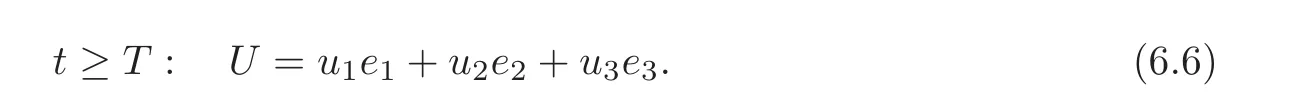
Since the invariant subspace Span{e1,e2,e3}of A is of dimension 3,it may contain one,two or three eigenvectors of A,thus we can distinguish the followings three cases.

(i)A admits three eigenvectors fr,gsand htcontained in Span{e1,e2,e3},corresponding to eigenvalues λ,µ and ν,respectively.Let f1,f2,···,fr;g1,g2,···,gsand h1,···,htbe the Jordan chains corresponding to these right eigenvectors:

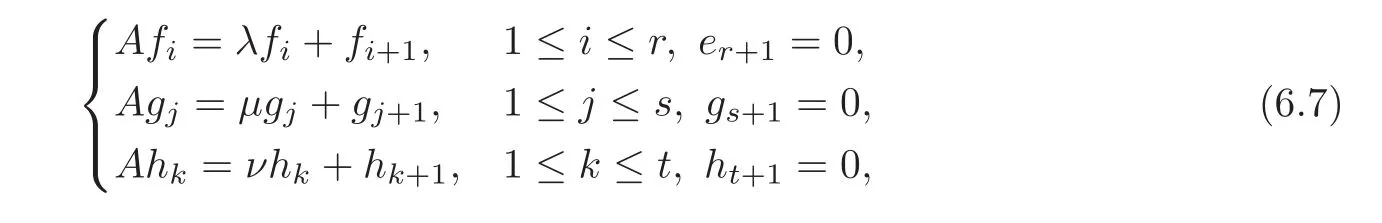
and let ξ1,ξ2,···,ξr;η1,η2,···,ηsand ζ1,ζ2,···,ζtbe the Jordan chains corresponding to the related left eigenvectors:

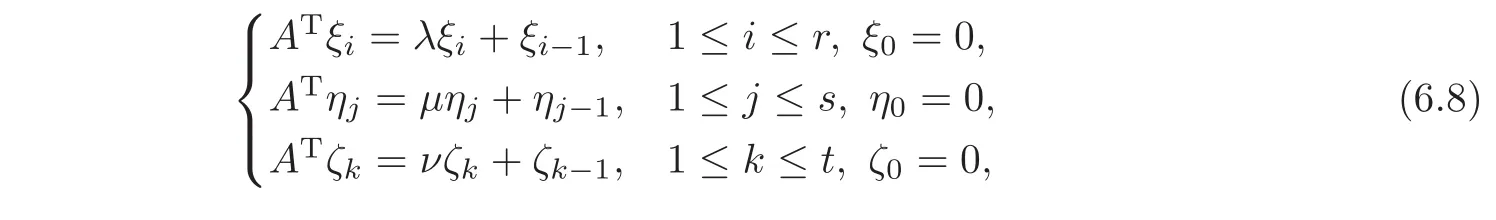
such that

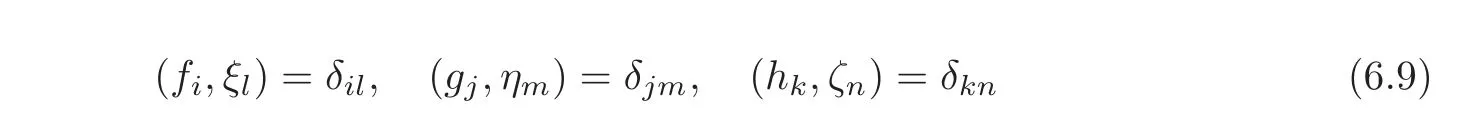
for i,l=1,···r;j,m=1,···s;k,n=1,···t and

for i=1,···r;j=1,···s;k=1,···t.

Taking the inner product with ξi,ηj,ζkon both sides of(1.1)—(1.2),respectively,and denoting

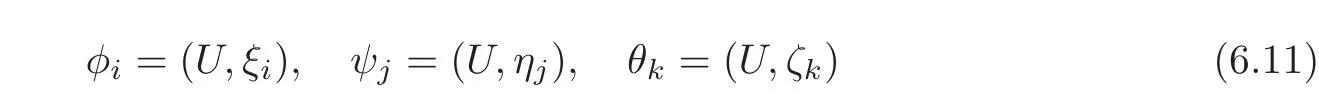
for i=1,···r;j=1,···s;k=1,···t,we get

Solving the reduced problems(6.12)—(6.14),we get φ1···,φr; ψ1,···,ψsand θ1,···,θt.Noting that fr,gs,htare contained in Span{e1,e2,e3},we have

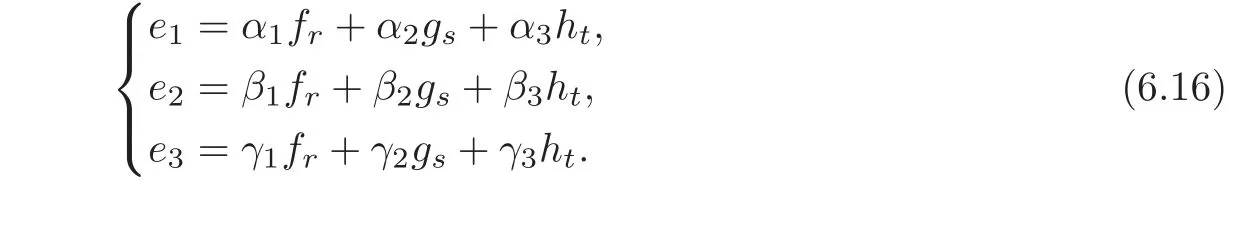
By(6.6)we have

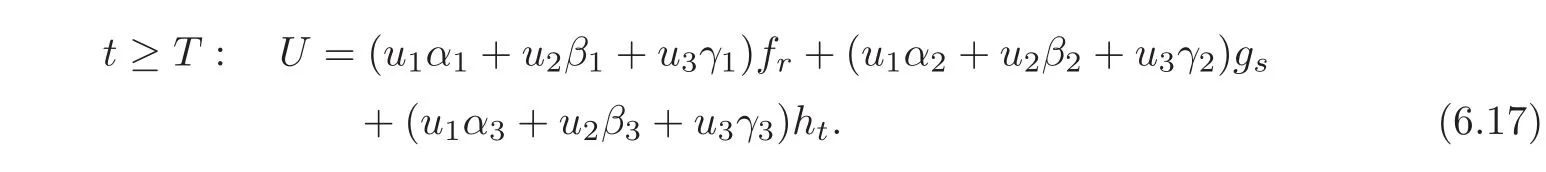
Noting(6.9)—(6.10),we have

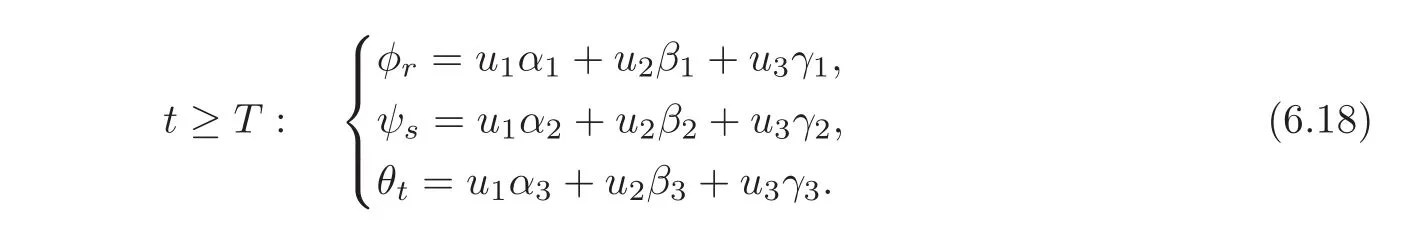
Since e1,e2,e3are linearly independent,the linear system(6.16)is invertible.Then,the state(u1,u2,u3)Tof synchronization by 3-groups can be determined by solving the linear system(6.18).

In particular,when r=s=t=1,the invariant subspace Span{ξ1,η1,ζ1}of ATis biorthonormal to Ker(C3)=Span{e1,e2,e3}.By Theorem 4.2,there exists a boundary control matrix D ∈DN−3,such that the state(u1,u2,u3)Tof synchronization by 3-groups is independent of the applied boundary controls.

(ii)A admits two eigenvectors frand gscontained in Span{e1,e2,e3},corresponding to eigenvalues λ and µ,respectively.Let f1,f2,···,frand g1,g2,···,gsbe the Jordan chains corresponding to these right eigenvectors:

and let ξ1,ξ2,···,ξr;η1,η2,···,ηsbe the Jordan chains corresponding to the related left eigenvectors:

such that

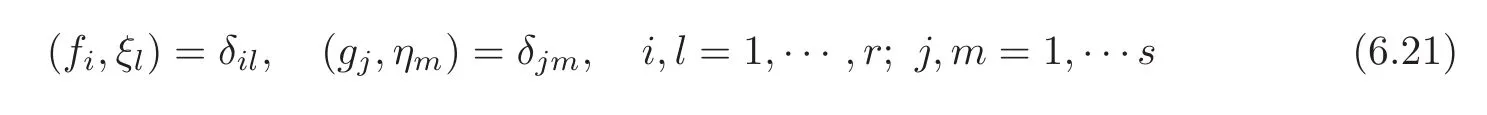
and

Taking the inner product with ξi, ηjon both sides of(1.1)—(1.2),respectively,and denoting

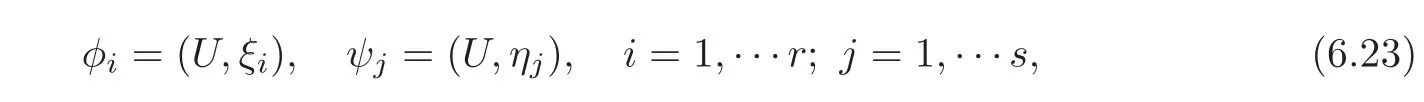
we get again the reduced problems(6.12)—(6.13).

In this case,since only two eigenvectors fr,gsare contained in the invariant subspace Span{e1,e2,e3}of dimension 3,either fr−1or gs−1is contained in Span{e1,e2,e3}.For fixing idea,we assume that fr−1is contained in Span{e1,e2,e3}.Then we have

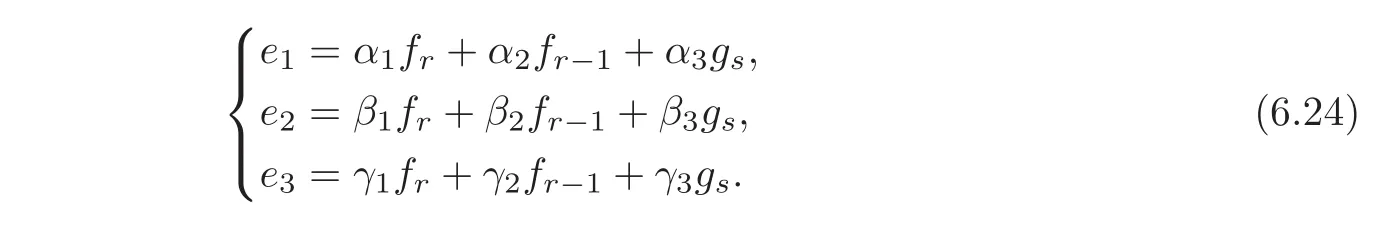
By(6.6)we have

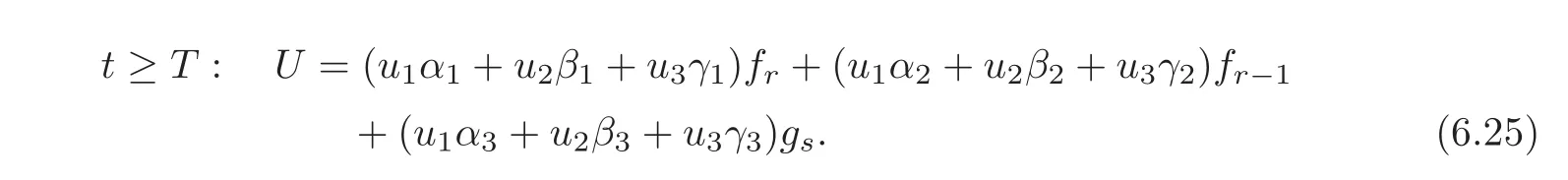
Noting(6.21)—(6.22),we have

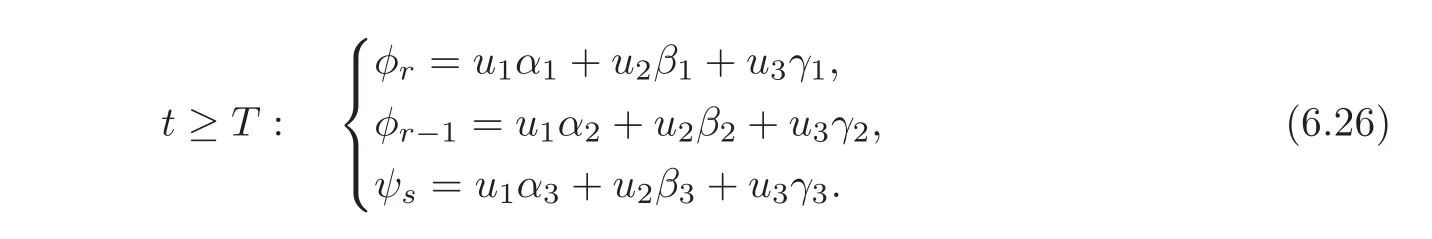
Since e1,e2,e3are linearly independent,the linear system(6.24)is invertible,then the state(u1,u2,u3)Tof synchronization by 3-groups can be determined by solving the linear system(6.26).

In particular,when r=2,s=1,the invariant subspace Span{ξ1,ξ2,η1}of ATis biorthonormal to Span{e1,e2,e3}.By Theorem 4.2,there exists a boundary control matrix D ∈DN−3,such that the state(u1,u2,u3)Tof synchronization by 3-groups is independent of the applied boundary controls.

(iii)A admits only one eigenvector frcontained in Span{e1,e2,e3},corresponding to the eigenvalue λ.Let f1,f2,···,frbe the Jordan chains corresponding to this right eigenvector:

and let ξ1,ξ2,···,ξrbe the Jordan chains corresponding to the related left eigenvector:

such that

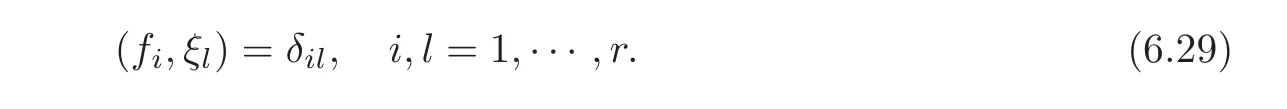
Taking the inner product with ξion both sides of(1.1)—(1.2),and denoting

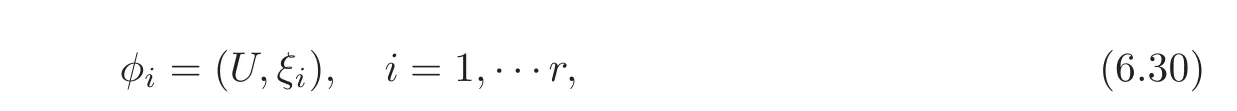
we get again the reduced problem(6.12).

In this case,since only one eigenvectorfris contained in the invariant subspace Span{e1,e2,e3}which is of dimension 3,fr−1and fr−2are necessarily contained in Span{e1,e2,e3},then we have

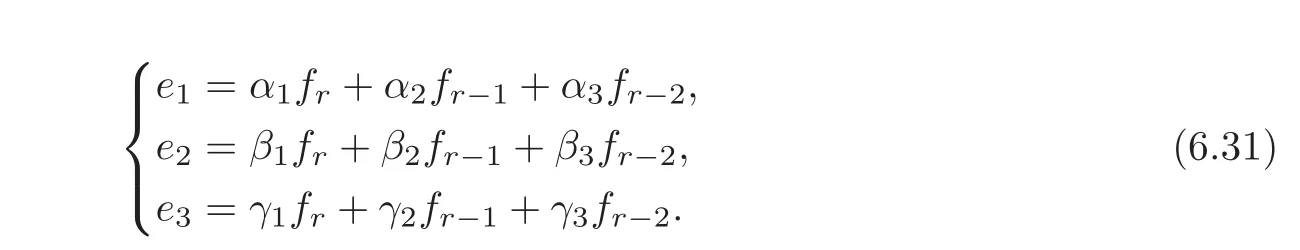
By(6.6)we have

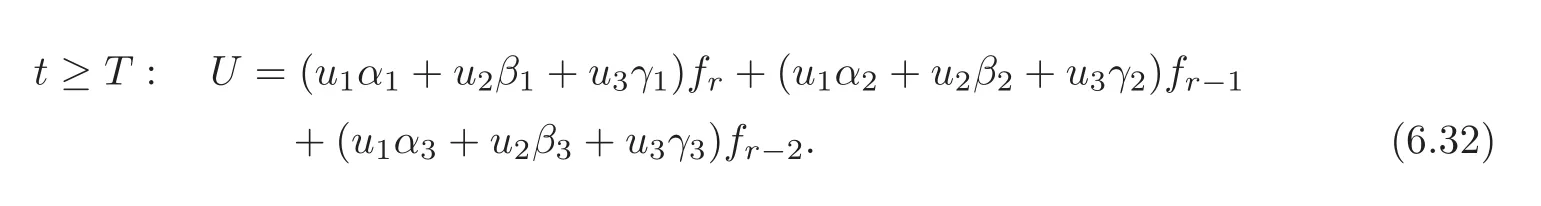
Noting(6.29),we have

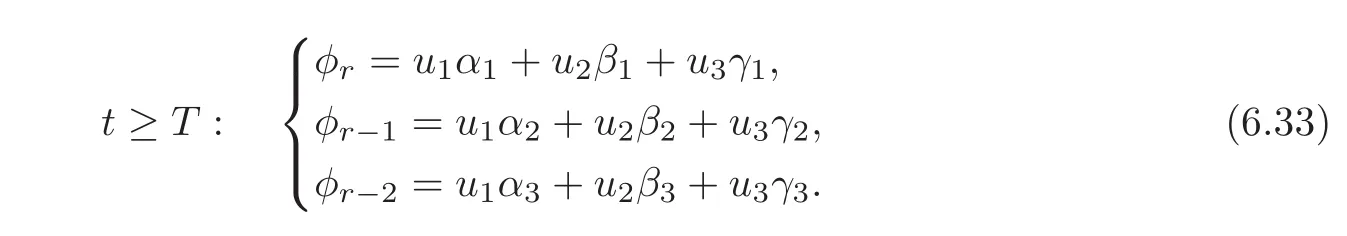
Since e1,e2,e3are linearly independent,the linear system(6.31)is invertible,then the state(u1,u2,u3)Tof synchronization by 3-groups can be determined by solving the linear system(6.33).

In particular,when r=3,the invariant subspace{ξ1,ξ2,ξ3}of ATis bi-orthonormal to Span{e1,e2,e3}.By Theorem 4.2,there exists a boundary control matrix D ∈DN−3,such that the state(u1,u2,u3)Tof synchronization by 3-groups is independent of the applied boundary controls.

[1]Bardos,C.,Lebeau,G.and Rauch,J.,Sharp sufficient conditions for the observation,control,and stabilization of waves from the boundary,SIAM J.Control Optim.,30,1992,1024–1065.

[2]Hu,L.,Li,T.-T.and Rao,B.P.,Exact boundary synchronization for a coupled system of 1-D wave equations with coupled boundary conditions of dissipative type,Communications on Pure and Applied Analysis,13,2014,881–901.

[3]Huygens,C.,Horologium Oscillatorium Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae,Apud F.Muguet,Parisiis,1673.

[4]Li,T.-T.and Rao,B.P.,Exaxt synchronization for a coupled system of wave equation with Dirichlet boundary controls,Chin.Ann.Math.,Ser.B,34(1),2013,139–160.

[5]Li,T.-T.and Rao,B.P.,A note on the exact synchronization by groups for a coupled system of wave equations,Math.Meth.Appl.Sci.,38(13),2015,2803–2808.

[6]Li,T.-T.and Rao,B.P.,On the exactly synchronizable state to a coupled system of wave equations,Portugaliae Math.,72,2015,83–100.

[7]Li,T.-T.and Rao,B.P.,Exact synchronization by groups for a coupled system of wave equations with Dirichlet boundary controls,J.Math.Pures Appl.,105(1),2016,86–101.

[8]Li,T.-T.and Rao,B.P.,Exact boundary controllability for a coupled system of wave equations with Neumann controls,Chin.Ann.Math.,Ser.B,38(2),2017,473–488.

[9]Li,T.-T.,Rao,B.P.and Hu,L.,Exact boundary synchronization for a coupled system of 1-D wave equations,ESAIM:Control,Optimisation and Calculus of Variations,20,2014,339–361.

[10]Li,T.-T.,Rao,B.P.and Wei,Y.M.,Generalized exact boundary synchronization for a coupled system of wave equations,Discrete Contin.Dyn.Syst.,34,2014,2893–2905.

[11]Lions,J.-L.and Magenes,E.,Non-homogeneous Boundary Value Problems and Applications,I,Springer-Verlag,New York,Heidelberg,1972.

[12]Pazy,A.,Semigroups of Linear Operators and Applications to Partial Differential Equations,Applied Mathematical Sciences,44,Springer-Verlag,New York,1983.

[13]Wiener,N.,Cybernetics,or Control and Communication in the Animal and the Machine,2nd ed.,the M.I.T.Press,Cambridge,Mass.,John Wiley&Sons,Inc.,New York,London,1961.