Gevrey Class Regularity of a Semigroup Associated with a Nonlinear Korteweg-de Vries Equation∗

Jixun CHUJean-Michel CORONPeipei SHANGShu-Xia TANG

(Dedicated to Philippe G.Ciarlet with admiration and friendship on the occasion of his 80th birthday)

1 Introduction

The motivation of this paper comes from the study of the asymptotic stability for the following nonlinear KdV equation posed on afinite spatial interval

where the space length L∈(0,∞).

When studying the asymptotic stability problem of nonlinear systems,a usual way is tofirstly do the linearization(around the origin)and study the asymptotic stability of the linearized system.By dropping the nonlinear term yyx,we obtain the associated linear system of(1.1)as follows:

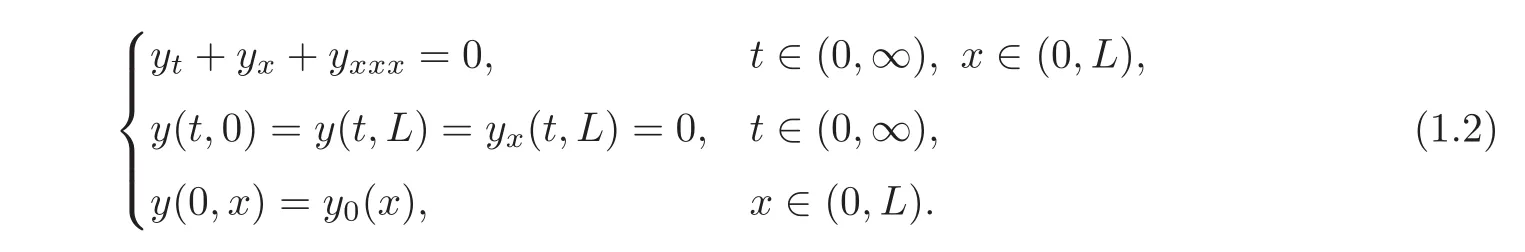
Set

Define the linear operator A:D(A)→ X by

with

It is easy to see that A is closed(see[6]).The well-posedness of(1.2)has been proved by Rosier[6]by showing that the linear operator A is the infinitesimal generator of a strongly continuous semigroup of contractions on L2(0,L).Moreover,he introduced in[6]the following set of critical lengths

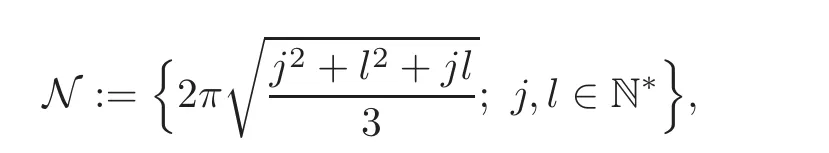
when considering the controllability problem where the control acts as Neumann boundary condition at the right end-point.

For the asymptotic stability of system(1.1),it was proved in[5]that when the space length L/∈N,0 is exponentially stable for the corresponding linearized equation(1.2),which gives the local asymptotic stability around the origin for the nonlinear system(1.1).When L∈N,the exponential stability of(1.2)does not hold because of the existence of afinite-dimensional space of solutions that are completely undamped.This is obtained by analyzing the spectrum of the linear operator A.To be more precise,it was proved in[6]that when L∈N,(1.2)admits a family of non-trivial solutions of the form y0(x)eλtfor some λ ∈ iR,where y0(x)satisfies

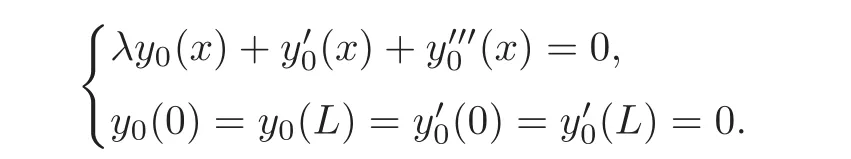
In this case,the origin of(1.2)is not asymptotically stable,and thus the linearization analysis fails.However,it is still very interesting to study the asymptotic properties of the nonlinear system(1.1)in this critical case.

In[2],we proved the existence and smoothness of the center manifold of(1.1)when L=2kπ,(i.e.,taking j=l=k in N),where k is a positive integer such that(see[3,Theorem 8.1,Remark 8.2])

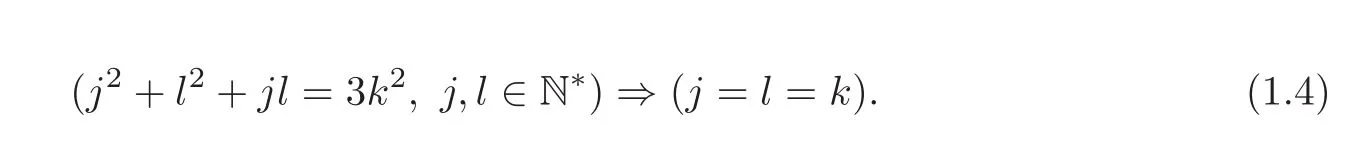
In this case,the center manifold is of dimension 1.By analyzing the reduced equation on the center manifold,we showed that the nonlinear system(1.1)is asymptotically stable around the origin with a polynomial decay rate.Using the same method,we proved in[7]the local asymptotic stability for another special critical length L=2π(i.e.,taking j=1,l=2 in N),where the center manifold is of dimension 2.

While studying the existence of the center manifold,it was noticed that the linear operator A does not generate an analytic semigroup,but a semigroup of Gevrey class.The Gevrey class of semigroups have a behavior somewhat “between” that of differentiable semigroups and analytic semigroups.For the convenience of readers,we first give the definition of Gevrey class δ＞1(see[1,8]).

Definition 1.1LetT(t)be a strongly continuous semigroup on a Banach spaceXand letδ＞ 1.We say thatT(t)is of Gevrey classδfort ＞ t0ifT(t)is infinitely differentiable fort∈ (t0,∞)and,for every compact subsetK ⊂ (t0,∞)and eachθ＞ 0,there exists a constantC=C(θ,K)such that

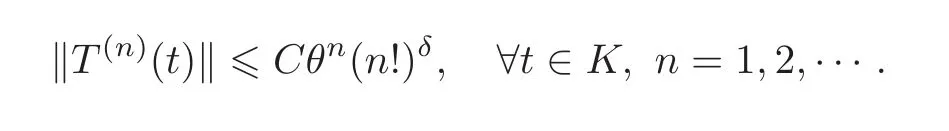
Whenδ=1,T(t)is analytic(see[9]).

With the definition of Gevrey class δ,we give the main result of this article.

Theorem 1.1The linear operatorAdefined by(1.3)does not generate an analytic semigroup but a semigroup of Gevrey classδfor everyδ＞fort＞ 0and for all lengthsL ∈ (0,∞).

The organization of the paper is as follows.In Section 2,we present some properties about the spectrum of the linear operator A and give the explicit formula for the resolvent of A.In Section 3,the estimation for the resolvent of A is proved in order to obtain our main result—Theorem 1.1.

2 Preliminary

In[2],we proved that for all L∈(0,∞),the spectrum of the linear operator A consists only of isolated eigenvalues offinite algebraic multiplicity.Moreover,the following lemma tells that for any fixed L ∈ (0,∞),there exists at most a finite number of eigenvalues on the imaginary axis.

Lemma 2.1For anyfixedL ∈ (0,∞),the following assertions hold:

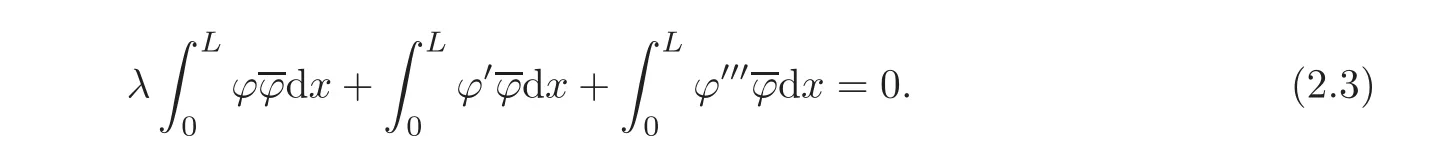
Taking the real part of(2.3),we have

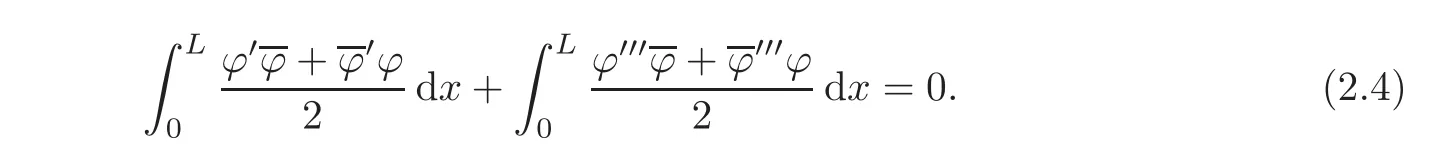
Integrating by parts in(2.4)and using(2.2),we get

Hence,λ ∈ σp(A)∩ iR if and only if there exists ϕ ∈ H3(0,L){0}such that

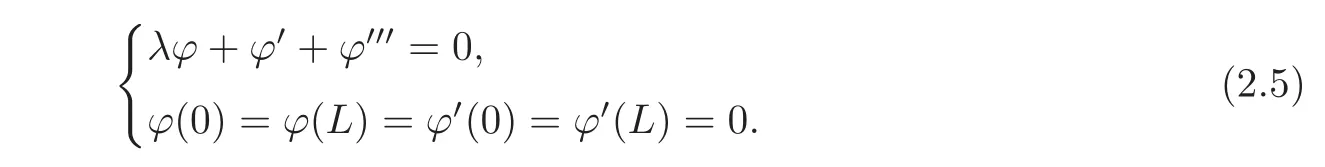
It was proved by Rosier[6,Lemma 3.5]that when L/∈N,there does not exist λ∈C,ϕ∈H3(0,L){0}such that(2.5)holds,thus we get that there are no eigenvalues of A on the imaginary axis and thefirst part of Lemma 2.1 follows.Moreover,when L ∈ N,we get from the proof of[6,Lemma 3.5]that there exist afinite number of eigenvalues of A on the imaginary axis which are given explicitly in(2.1),thus the rest of this lemma follows.

From Lemma 2.1,we get immediately the following result,where ρ(A)is the resolvent set of the closed operator A,i.e.,the set of λ ∈ C for which λI− A has a bounded inverse,I denoting the identity map.

Lemma 2.2There existsω0＞ 0such thatiω ∈ ρ(A)whenever|ω|≥ ω0.

Concerning the explicit formula for the resolvent of A,we have the following lemma.

Lemma 2.3For eachλ ∈ ρ(A),denote bypi,i=1,2,3the three roots of3λ+p+p=0,and set

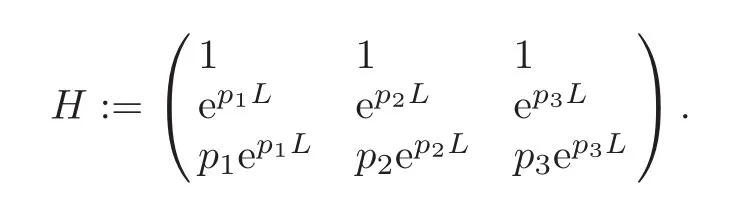
Then we havepi/=pjwheni/=j,and

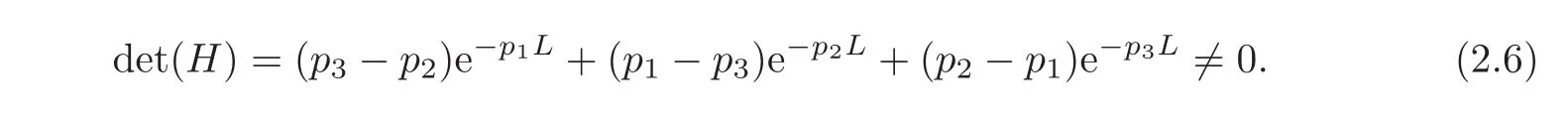
Moreover,the resolvent ofAis given by

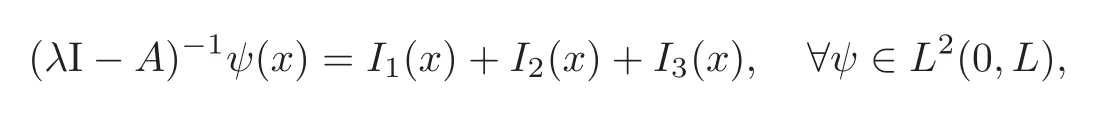
where

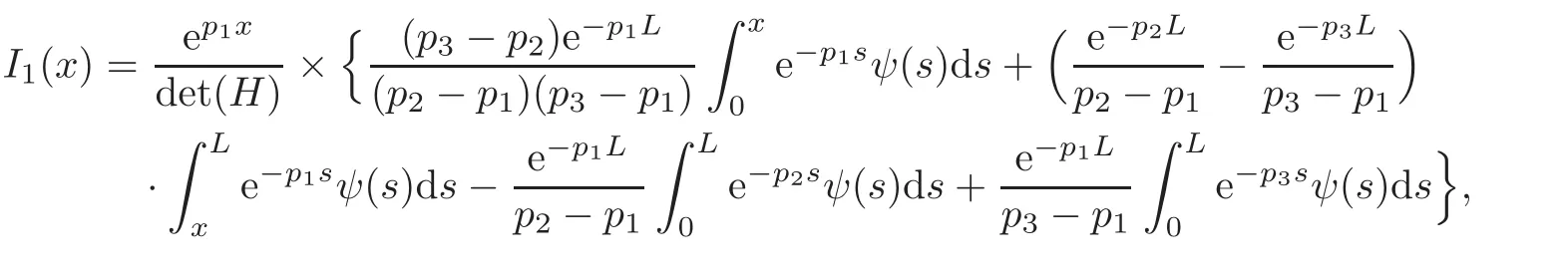
ProofSuppose that λ ∈ ρ(A).Then for any ψ ∈ L2(0,L),there exists a ϕ ∈ D(A)such that

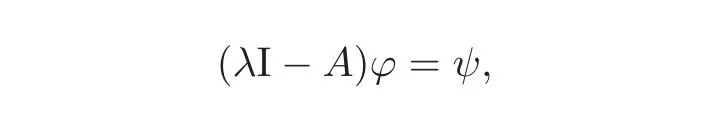
i.e.,

We consider the homogeneous differential equation associated with(2.7)

The characteristic equation of(2.8)is λ+p+p3=0.Using our notation,we have

Here and hereafter,we denote by C1,C2and C3arbitrary constants.Using the method of variation of constant,the general solution of(2.7)is supposed to be

with C1(x),C2(x)and C3(x)satisfying

We deduce from(2.11)that

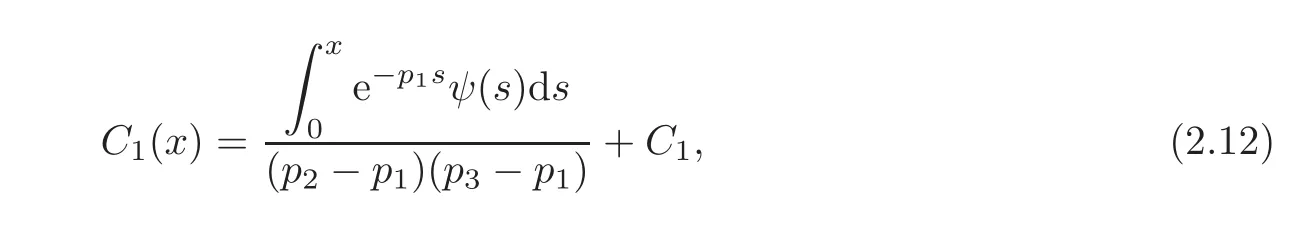
We now determine C1,C2and C3by using the boundary conditions in(2.7).Using(2.7),together with(2.10)and(2.12)—(2.14)gives

and

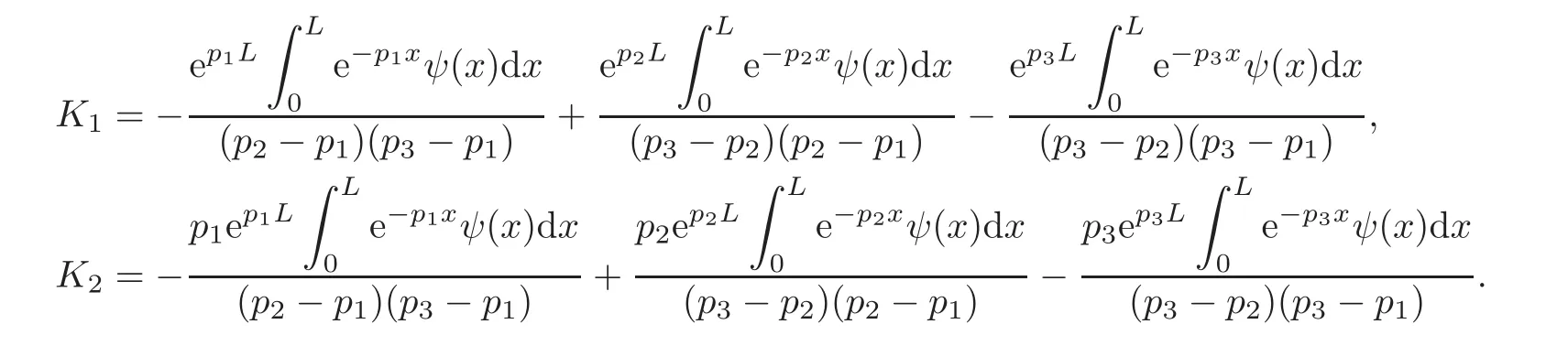
Since λ ∈ ρ(A),it is clear that det(H)/=0.Then,we can determine C1,C2and C3through(2.15)uniquely.To be more precise,we have

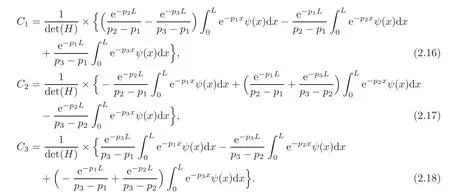
Combining(2.10),(2.12)—(2.14)and(2.16)—(2.18),the result of Lemma 2.3 follows directly.

3 Estimation of the Resolvent

It is usually difficult to identify the Gevrey class regularity for a given strongly continuous semigroup with Definition 1.1.In this paper,we will refer to the following sufficient condition for a strongly continuous semigroup to be of Gevrey class.It is based on the estimation for the resolvent of its infinitesimal generator.

Theorem 3.1(see[8,Theorem 4,p.153])LetT(t)be a strongly continuous semigroup satisfying‖T(t)‖ ≤ Meνt.Suppose that,for someµ ≥ νandαsatisfying0＜ α ≤ 1,

ThenT(t)is of Gevrey classδfort＞0,for everyδ＞.

From Lemma 2.2,we know that when|ω|is large enough,iω ∈ ρ(A).Then for each ψ ∈ L2(0,L),the explicit formula of(iωI− A)−1ψ is obtained by Lemma 2.3.From this formula,we can get the following estimate for the resolvent.

Theorem 3.2For anyfixedL ∈ (0,∞),there exist positive constantsω1＞ 0,M1≥ M2＞0,such that for allω ∈ Rwith|ω|≥ ω1,the following inequality holds:

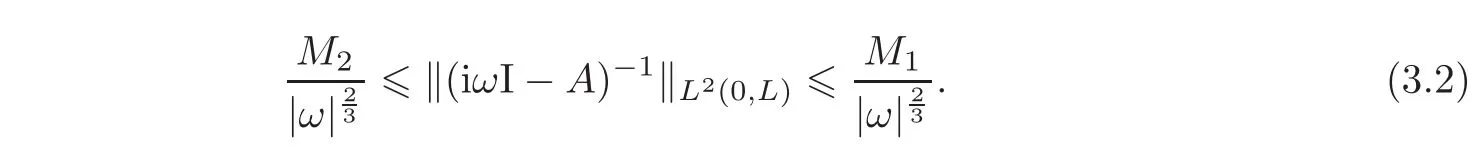
In particular,using Theorem3.1withM=1,µ = ν =0andα =,the linear operatorAgenerates aC0-semigroup of Gevrey classδ∈ ?,∞）fort＞ 0.

Remark 3.1From the left-hand side of estimation(3.2),we get that the linear operator A does not generate an analytic semigroup(see[4,Theorem 5.2]).

Remark 3.2To our knowledge,no equivalence exists between the estimate of the resolvent(3.2)and the Gevrey class regularity.Thus,we were unable to confirm the optimality of the value.

Proof of Theorem 3.2Without loss of generality,we consider the case where λ =iω with ω ＞ 0.Similar estimates can be obtained for λ =iω with ω ＜ 0.We still denote by p1,p2and p3the three roots of

Let,for j∈ {1,2,3}and ω ＞ 0,

Then qjis the solution of

Applying the implicit function theorem to(3.5),we get that there exist ω1＞ 0 and C(ω1)＞ 0 such that

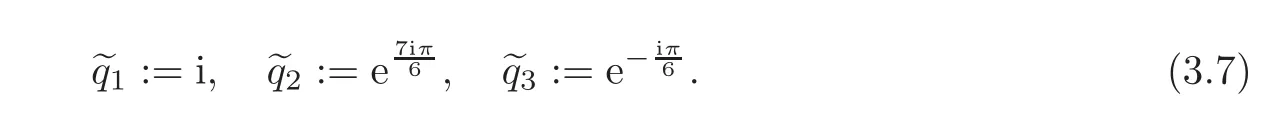
By(3.4)and(3.6)—(3.7),we get

and for ω ＞ ω1large enough that

Moreover,from(3.4)and(3.6)—(3.7),we obtain that for i/=j,

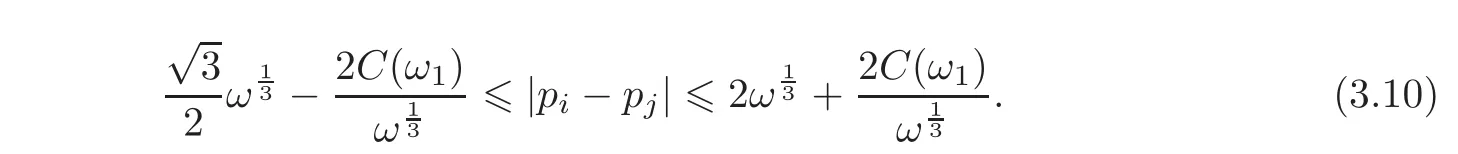
Next,we estimate the norm of the resolvent(iωI− A)−1.Since for each ψ ∈ L2(0,L),

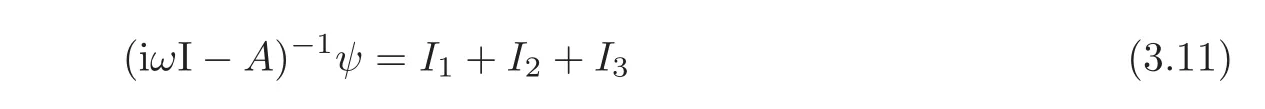
with I1,I2and I3defined in Lemma 2.3,we have

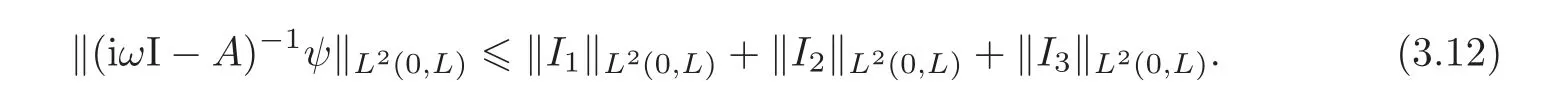
By the expression of I1in Lemma 2.3,noticing(3.8)and(3.9),we obtain through Hö lder’s inequality that

Here and hereafter,Θ denotes various positive constants which may depend on L and ω1,but do not depend on ψ and ω.We obtain from(3.8)to(3.10)and the expression of det(H)in(2.6)that for ω large enough

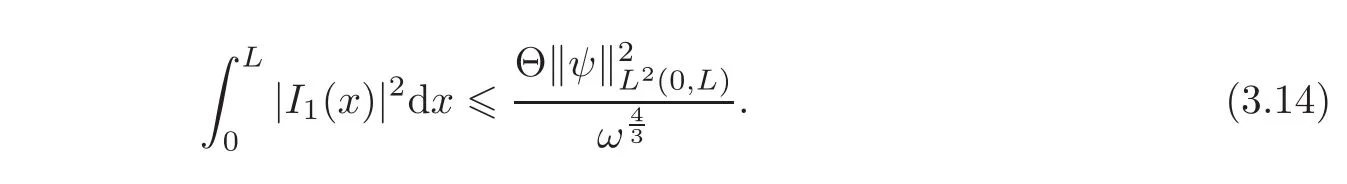
Similarly,by the expression of I2in Lemma 2.3,we have

For the estimation of the first term in(3.15),using Hö lder’s inequality and(3.9),we have

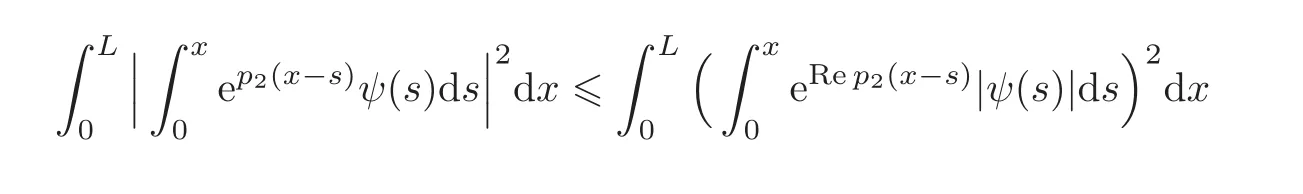
By(3.9),we get

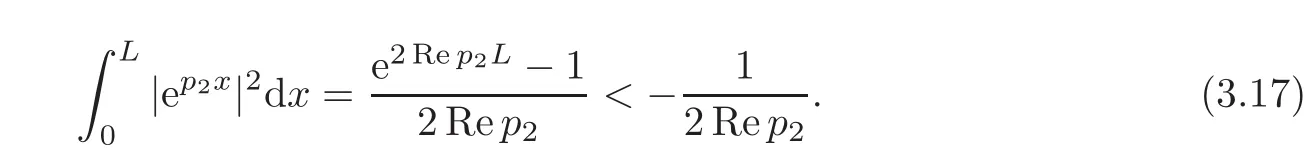
For the estimation of the third term in(3.15),we obtain through Hö lder’s inequality and(3.9)that

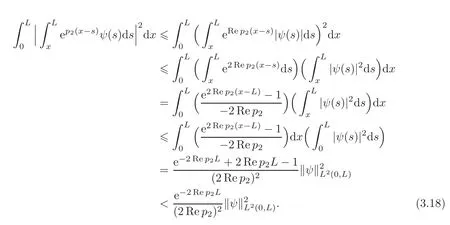
Combining(3.15)to(3.18),by(3.8)—(3.10)and the expression of det(H)in(2.6),we deduce that

Let us emphasize that,from(3.9),Rep2＜0 while Rep3＞0.Therefore we cannot deduce the estimates for ‖I3‖L2(0,L)from the estimates for ‖I2‖L2(0,L)directly.Thus,we have to directly estimate ‖I3‖L2(0,L).By the expression of I3in Lemma 2.3,we have

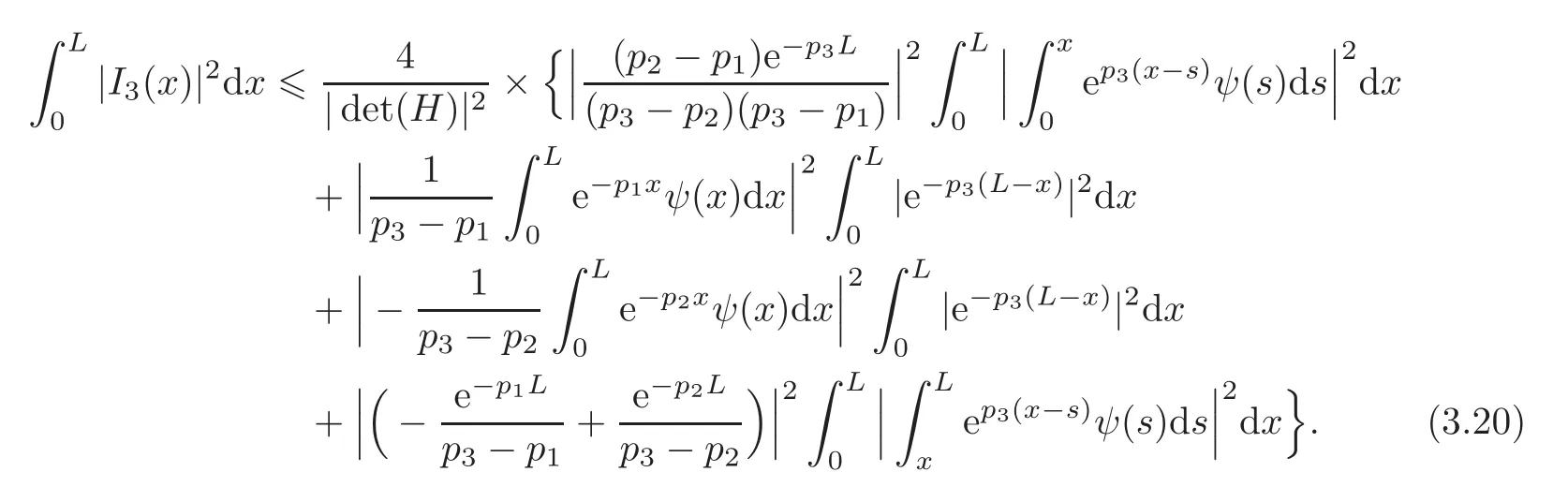
For the estimation of the first term in(3.20),noticing(3.9),we get through Hö lder’s inequality that

By(3.9),we get

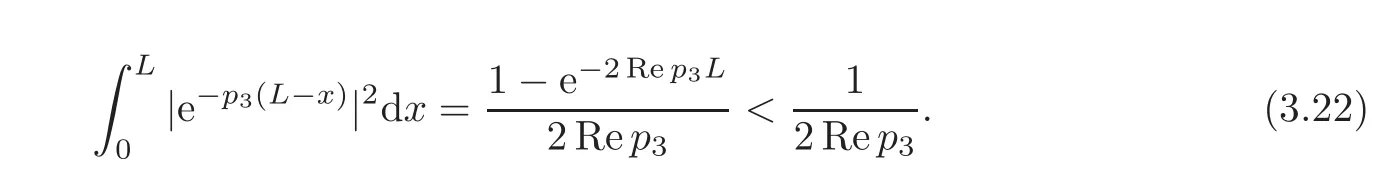
For the estimation of the last term in(3.20),we get through Hö lder’s inequality and(3.9)that

Combining(3.20)to(3.23),we obtain through(3.8)to(3.10)that

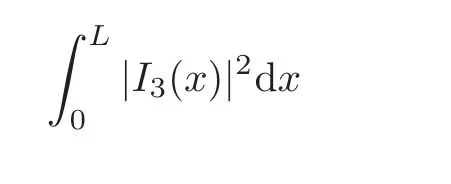
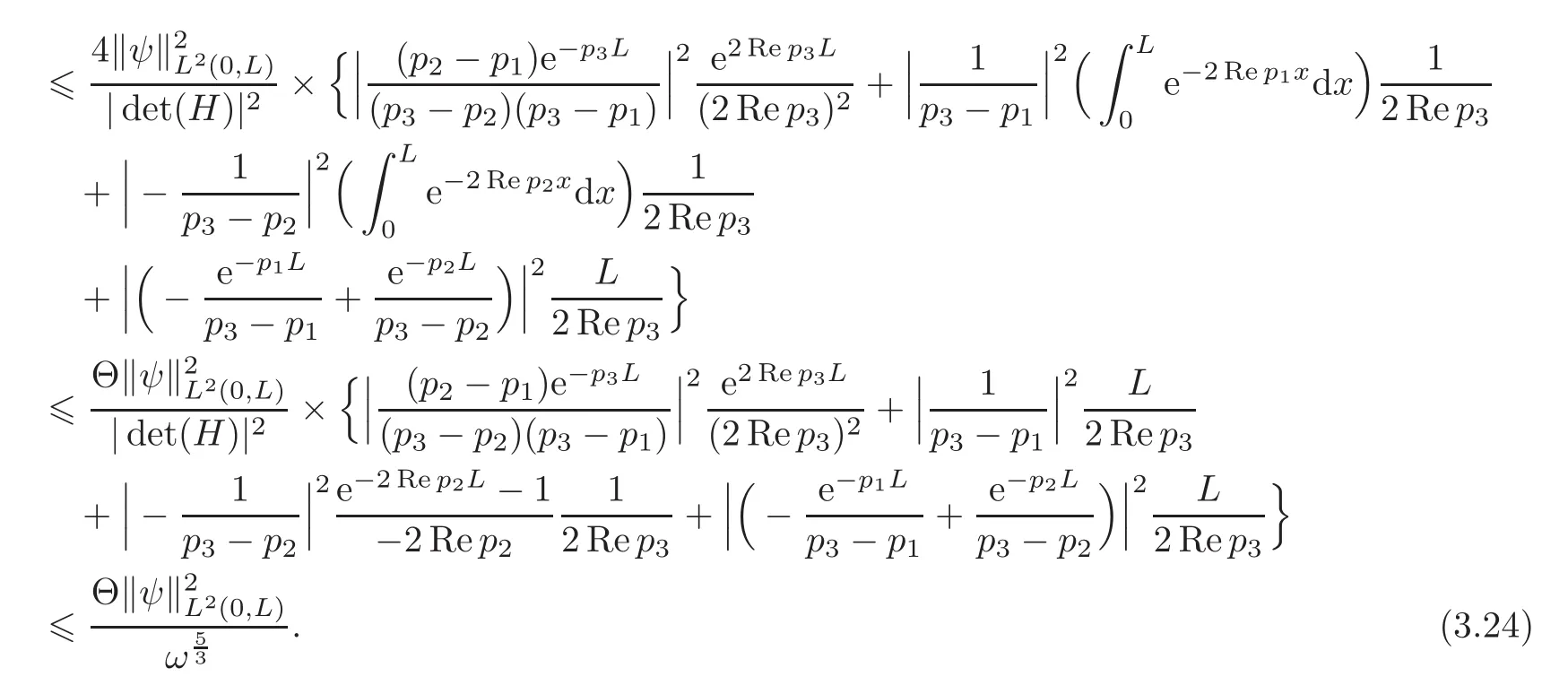
Using(3.12),(3.14),(3.19)and(3.24),the right-hand side of estimation(3.2)follows.

In order to obtain the left-hand side of estimation(3.2),let ψ(x)=ep1xand we get

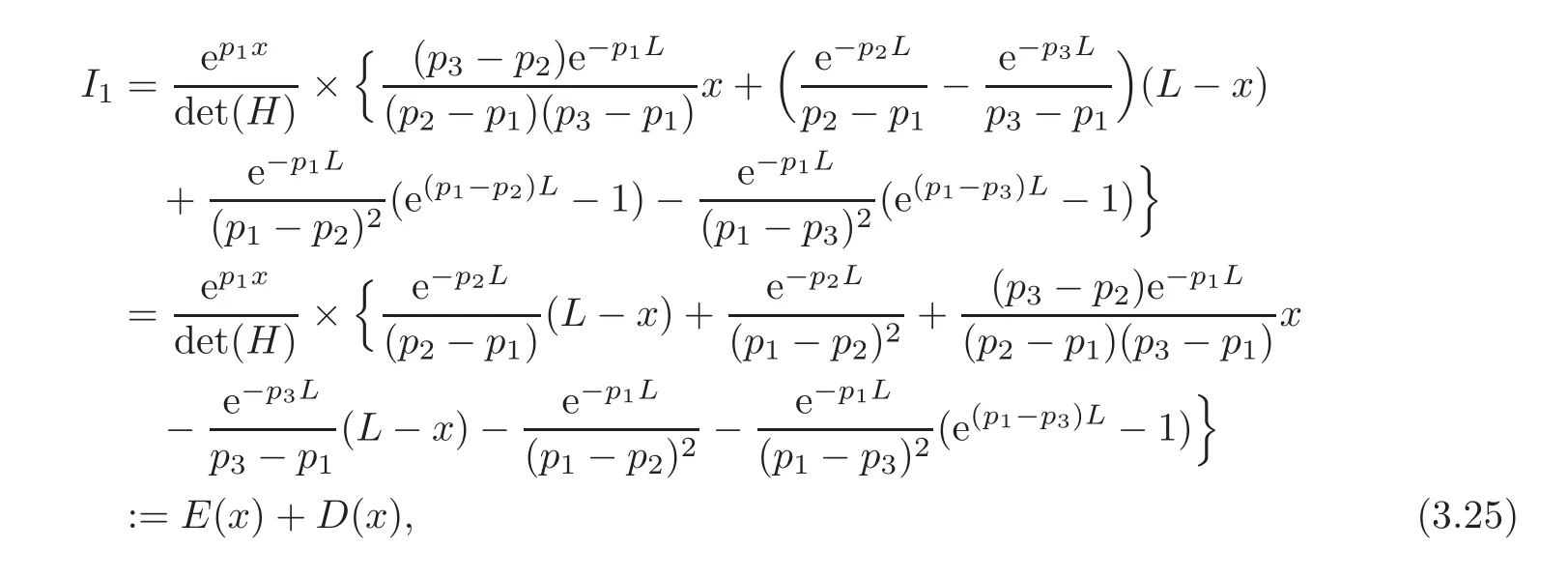
where

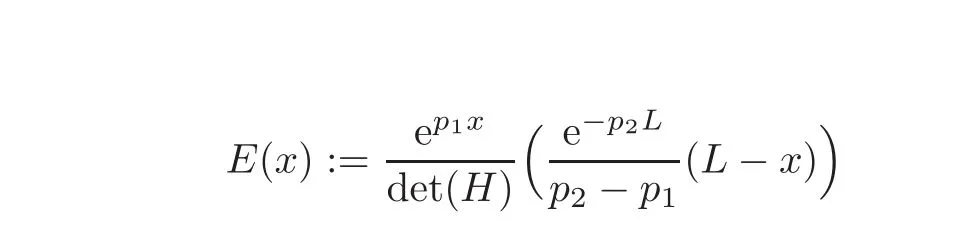
and

Moreover,by(3.9)—(3.10)and the expression of det(H)in(2.6),we have

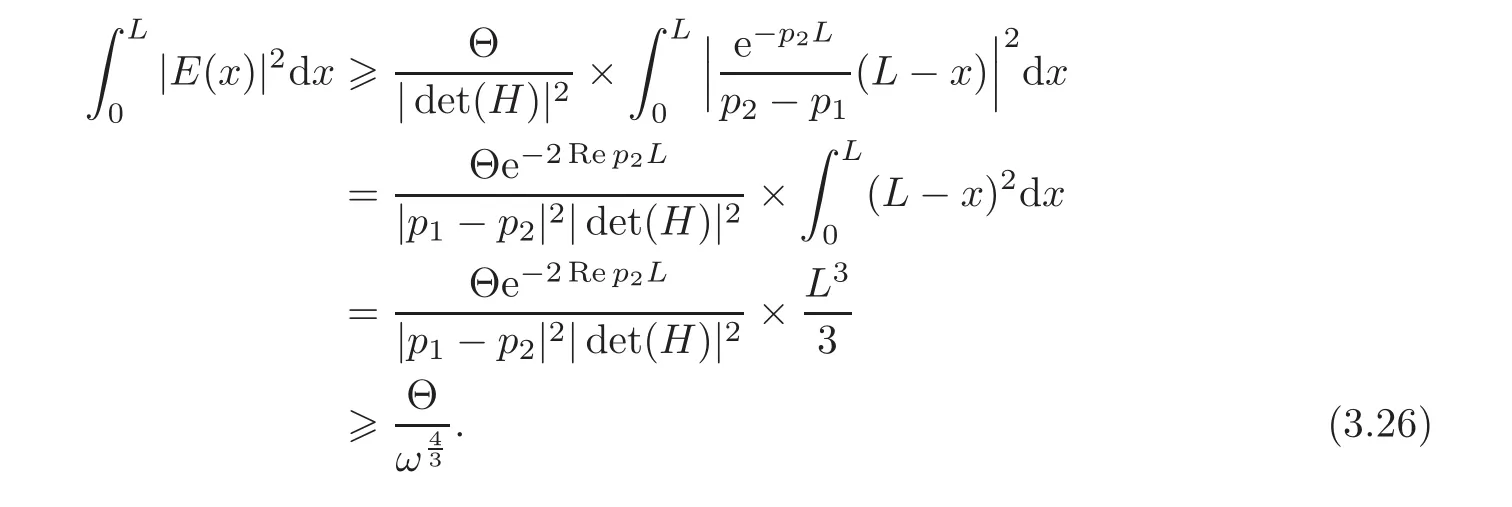
Using again(3.8)to(3.10)and the expression of det(H)in(2.6),we get

Combining(3.11),(3.19),(3.24)to(3.27),and noticing

we get that the left-hand side of estimation(3.2)holds.The proof of Theorem 3.2 is completed.

AcknowledgementThe authors thank Bingyu Zhang for his interesting comments and many valuable suggestions on this work.

[1]Belinskiy,B.and Lasiecka,I.,Gevrey’s and trace regularity of a semigroup associated with beam equation and non-monotone boundary conditions,J.Math.Anal.Appl.,332(1),2007,137–154.

[2]Chu,J.X.,Coron,J.-M.and Shang,P.,Asymptotical stability of a nonlinear Korteweg-de Vries equation with critical lengths,J.Diff.Eq.,259(8),2015,4045–4085.

[3]Coron,J.-M.,Control and nonlinearity,Mathematical Surveys and Monographs,136,American Mathematical Society,Providence,RI,2007.

[4]Pazy,A.,Semigroups of linear operators and applications to partial differential equations,Applied Mathematical Sciences,44,Springer-Verlag,New York,1983.

[5]Perla Menzala,G.,Vasconcellos,C.F.and Zuazua,E.,Stabilization of the Korteweg-de Vries equation with localized damping,Quart.Appl.Math.,60(1),2002,111–129.

[6]Rosier,L.,Exact boundary controllability for the Korteweg-de Vries equation on a bounded domain,ESAIM Control Optim.Calc.Var.,2,1997,33–55(electronic).

[7]Tang,S.-X.,Chu,J.X.,Shang,P.and Coron,J.-M.,Asymptotic stability of a Korteweg-de Vries equation with a two-dimensional center manifold,Adv.Nonlinear Anal.,2016,DOI:10.1515/anona-2016-0097.

[8]Taylor,S.,Gevrey regularity of solutions of evolution equations and boundary controllability,Gevrey semigroups(Chapter 5),Ph.D Thesis,School of Mathematics,University of Minnesota,1989.

[9]Zhang,Q.,Wang,J.-M.and Guo,B.-Z.,Stabilization of the Euler-Bernoulli equation via boundary connection with heat equation,Math.Control Signals Systems,26(1),2014,77–118.