An Energy Stable Monolithic Eulerian Fluid-Structure Numerical Scheme

Olivier PIRONNEAU

(Dedicated to Philippe G.Ciarlet on the occasion of his 80th birthday)

1 Introduction

Currently two methods dominate FSI(Fluid-Structure-Interaction)science:Arbitrary Lagrangian Eulerian(ALE for short)methods especially for thin structures(see[17,28])and immersed boundary methods(IBM for short)(see[11,29]),for which the mathematical analysis is more advanced(see[5])but the numerical implementations lag behind.ALE for large displacements have meshing difficulties(see[25])and to a lesser extent with the matching conditions at thefluid-solid interface(see[23]).Furthermore,iterative solvers for ALE-based FSI methods which rely on alternative solutions of thefluid and the structure parts are subject to the added mass effect and require special solvers(see[7,16]).

Alternatives to ALE and IBM are few.One old method(see[2—3])has resurfaced recently,the so-called actualized Lagrangian methods for computing structures(see[22,26]),see also[10]although different from the present study because it deals mostly with membranes.

Continuum mechanics does not distinguish between solids andfluids till it comes to the constitutive equations.This has been exploited numerically in several studies but most often in the context of ALE(see[21,24,32]).

In the present study,which is a follow-up of[30]and[19],we investigate what Stephan Turek[21],Heil[20]and Wang[34]called a monolithic formulation but here in an Eulerian framework,as in[13—15,31],following the displaced geometry of the fluid and the solid.In[13],the authors obtained excellent results with the fully Eulerian formulation adopted here but at the cost of meshing difficulties to handle the Lagrangian derivatives.Here we advocate the Characteristic-Galerkin method and obtain an energy estimate,which is not a proof of stability but a prerequisite for it.

2 Conservation Laws

The following standard notations are used.For more details see one of textbooks:[1—2,9,27],or the following articles:[21,24].For clarity we use bold characters for vectors and tensors/matrices,with some exceptions,like x,x0∈Rd,d=2 or 3.

We denote by trAand detAthe trace and determinant of A.To describe thefluid structure system we need the following:

Finally and unless specified all spatial derivatives are with respect to x ∈ Ωtand not with respect to x0∈ Ω0.Let φ a function of x,t;as x=X(x0,t),x0∈ Ω0,φ is also a function of x0and we have

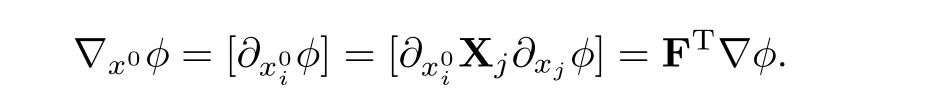
When X is one-to-one and invertible,d and F can be seen as functions of(x,t)instead of(x0,t).They are related by

Time derivatives are related by(note the notation Dt)

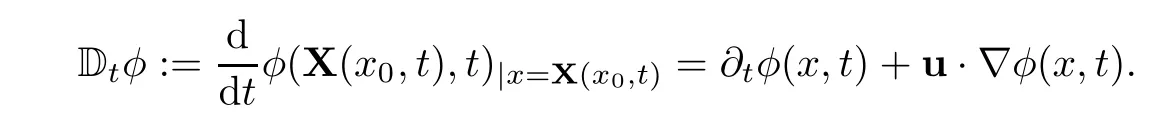
It is convenient to introduce(note the difference between Dtabove and D here):

Conservation of momentum and conservation of mass take the same form for thefluid and the solid:

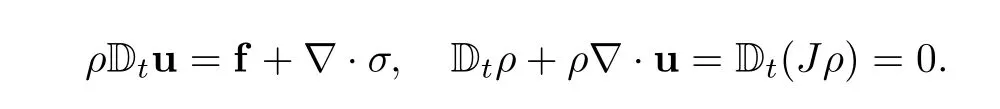
So Jρ= ρ0at all times

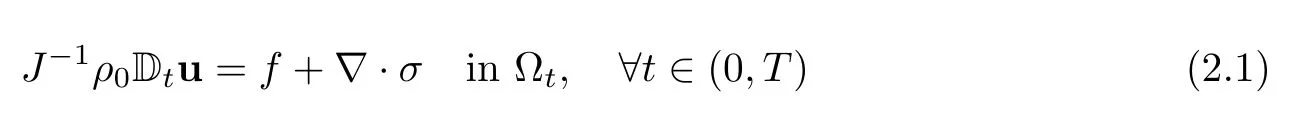
with continuity of u and of σ ·n at the fluid-structure interface Σ in absence of interface constraint like surface tension.There are also unwritten constraints pertaining to the realisability of the map X(see[9,27]).

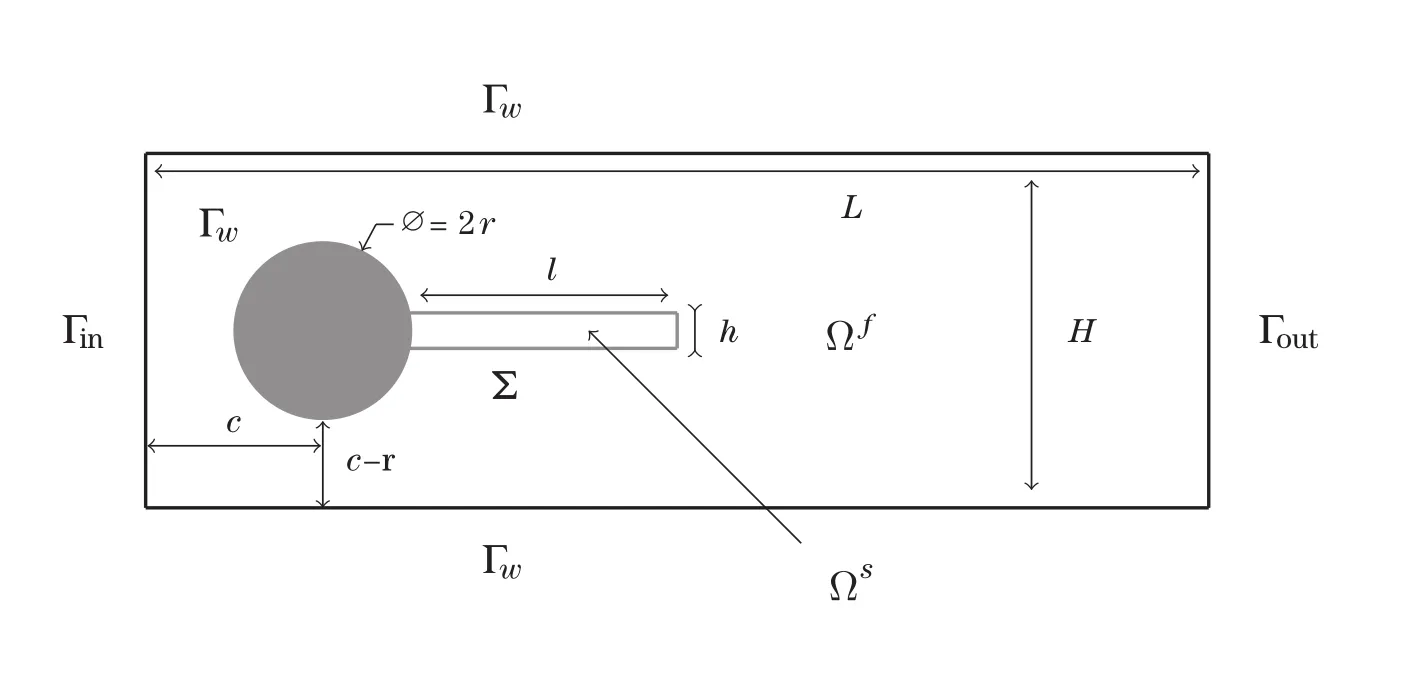
Figure 1 The geometry of the FLUSTRUK test(see[15]).The cylinder(in black)isfixed but the flag is a thick compressible Mooney-Rivlin material clamped to the cylinder by its left boundary;the outer rectangle isfilled with afluid which enters from the left Γinand leaves on the right Γout;the horizontal boundaries of the outer rectangle are walls,so they form together with the cylinder the boundary Γw.The flag is at time zero a rectangle of size l×h.The outer rectangle has size L×H.The center of the circle representing the cylinder is at(c,c)in a frame of reference which has the lower left corner at(0,0);the cylinder has radius r and isfixed.

2.1 Constitutive equations

We consider a bi-dimensional geometry.For the 3d case(see[8]).

•For a Newtonian incompressiblefluid:σf= −pfI+µfDu,

• For an hyperelastic material:σs= ρs∂FΨFT,

where Ψ is the Helmholtz potential which,in the case of a St-Venant-Kirchhoff material,is(see[9])

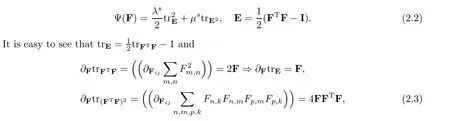
which implies that∂FtrE2=2FE.Therefore

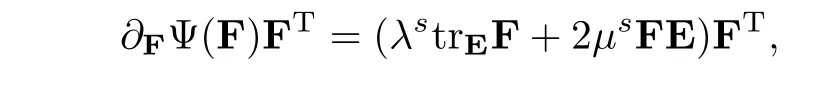
which in turn implies that

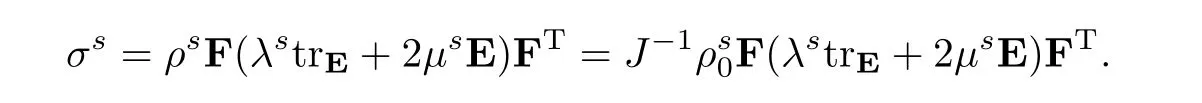
Remark 2.1Some authors have a different definition for the Lam´e coefficient λρs0→ λ,→ µ which define σs.

Proposition 2.1Letγ=trFFT.Then

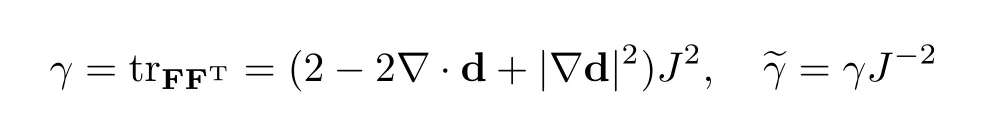
and the following holds

with

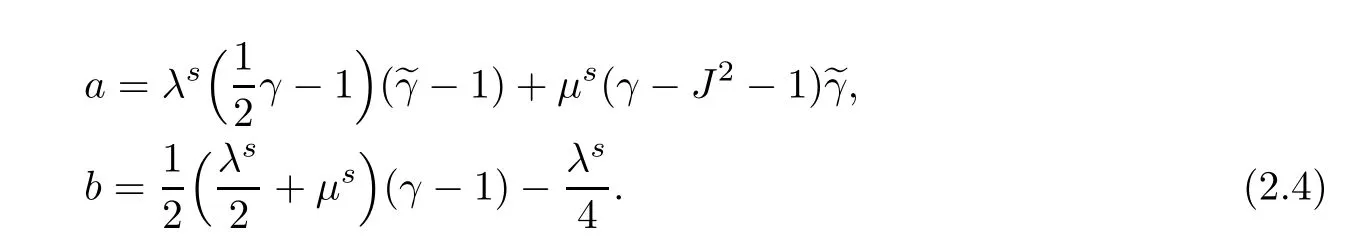
ProofFirst note that if B=FFTthen

Now by the Cayley-Hamilton theorem in 2-dimensions,B2−γB+J2I=0.As

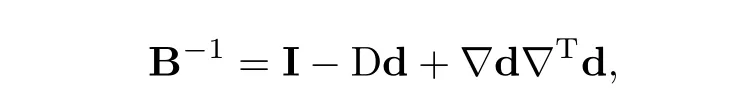
let C=I−B−1=Dd−∇d∇Td.Then

Therefore

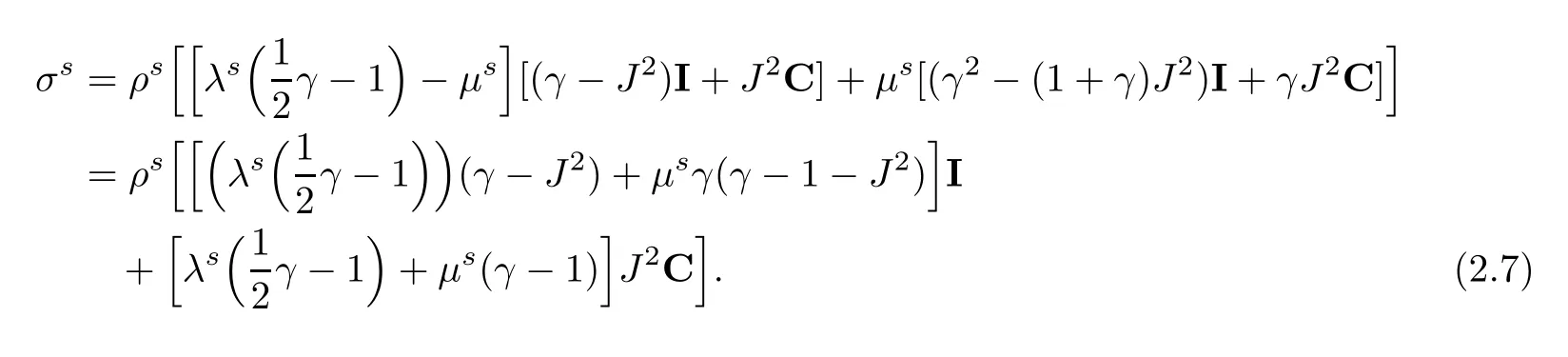
2.2 Variational monolithic Eulerian formulation

From now on we limit our analysis to the case,constant.

One must find(u,p)with u|Γ=0,d and,Ωf,solution for allwith=0 of

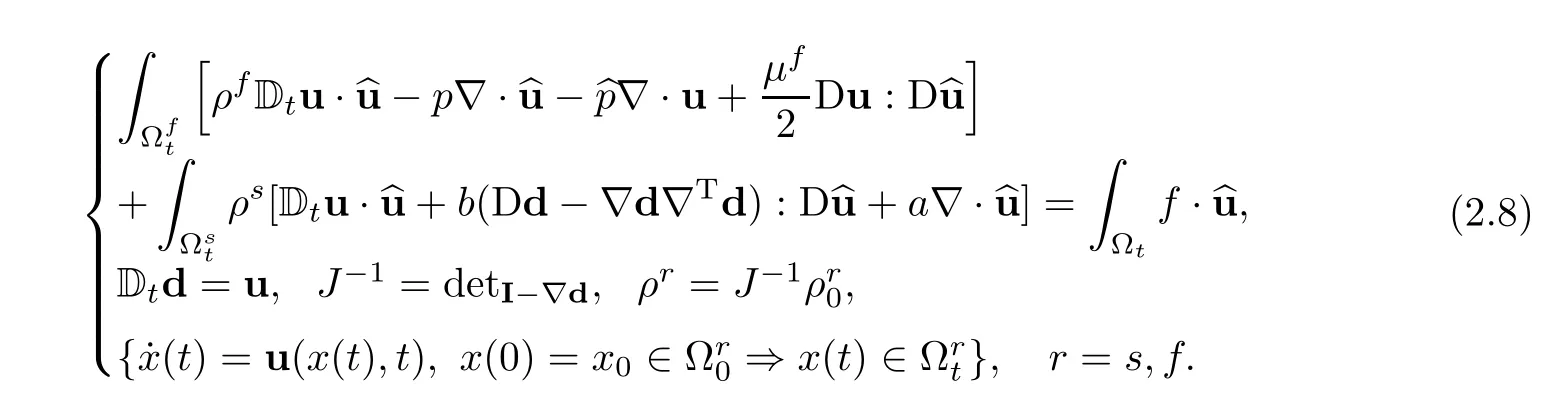
For an existence result,up to time T∗(see[6,12,33]),provided a regularization term is added to the formulation to insure that∂td has H1-regularity;T∗is such that the solid does not touch the boundary and Σtdoes not buckle.

3 Numerical Scheme

For the stability of the numerical scheme,the problem is that even for small displacements the Lam´e termsvariational formulation(2.8).

But notice that

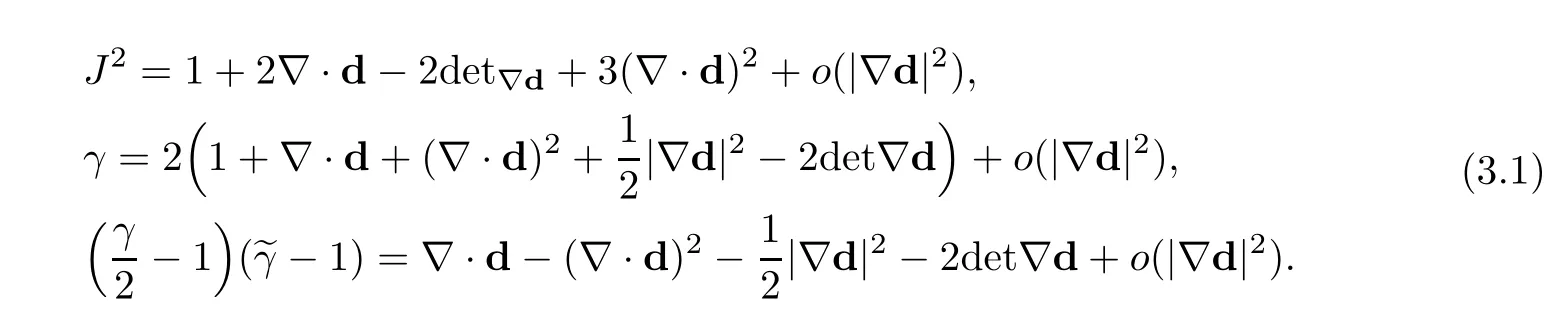
So it makes sense to define

To prepare the time discretisation of(2.8)with a given time step δt,let

Then(2.8)becomes

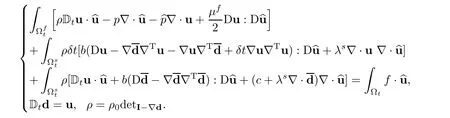
Here linear elasticity is visible because the zero order term of b isFrom now on we do not use d because the Characteristics-Galerkin discretisation of Dtd=u will give an analogue of(3.3).

3.1 Discretisation of total derivatives

Let Ω ⊂ Rd,(d=2 here),t∈ (0,T)and x ∈ Ω.Then let(τ)be the solution at time τ of

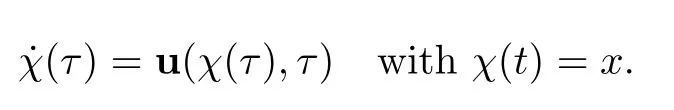
If u is Lipschitz in space and continuous in time the solution exists.The Characteristics-Galerkin method relies on the concept of total derivative:

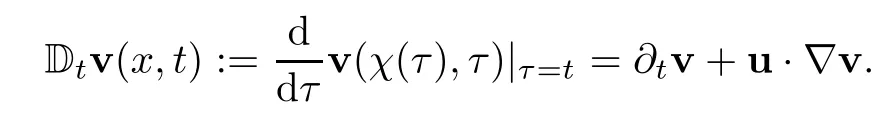
Given a time step δt,let us approximate

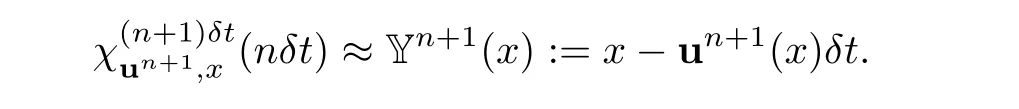
Remark 3.1Note also that,as Jρ is convected by u,that is Jρ|χtu,x(τ),τ=Jρ|x,t,so a consistent approximation is

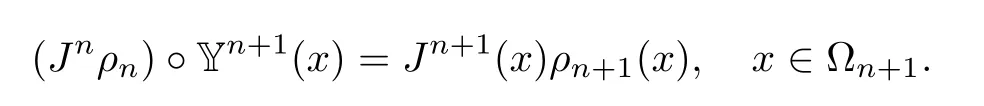
Thus discretising the total derivative of u or the one of ρ0u will give the same scheme.

3.2 Updating thefluid and solid domain

From the definition of Y,notice that the only way to be consistent is to define Ωn+1using un+1,i.e.,implicitly,since the later is defined also on Ωn+1:

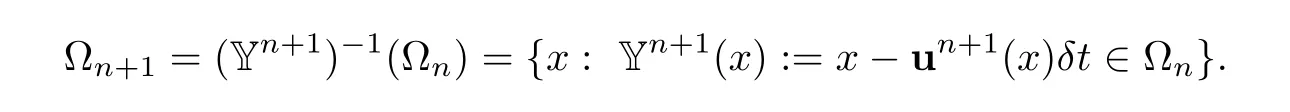
3.3 The time discretised scheme

Let

3.4 Iterative solution byfixed point

The most natural method to solve the above is to freeze some coefficients so as to obtain a well posed linear problem and iterate:

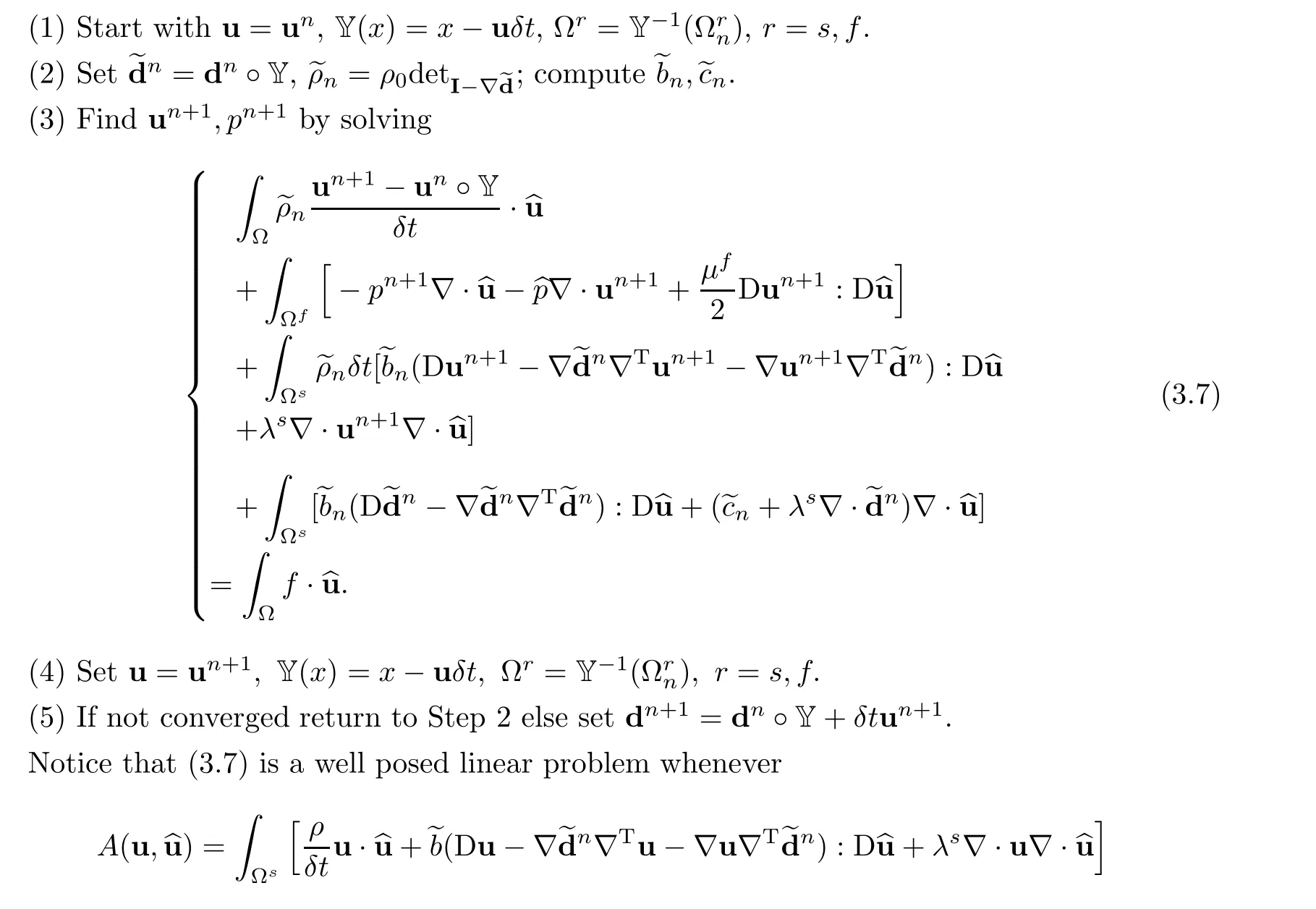
is coercive.Then(3.7)gives a solution bounded in H1(Ω)and converging subsequences can be extracted fromisfixed.Then convergence would occur if we could prove thatconverges.

3.5 Spatial discretisation withfinite elements

3.6 Implementation

The various tests we made lead us to recommend the following.

•Move the vertices of the triangles supporting the solid with their own velocity:

which,as explained above has to be implemented through an iterative process.

•Remesh thefluid part at each iteration with a Delaunay-Voronoi mesh generator from the boundary vertices of Σn+1.However in a Eulerian formulation there is only one mesh,even if the triangles are marked to be fluid or structure.Hence the fluid boundary must be identified computationally,its oriented edges and vertices;these are then input to thefluid mesh generator as if it was the boundary of an independentfluid domain.Finally two new meshes are merged into a uniquefluid-structure mesh.

•In doing so,the discrete topological properties of the structural part are preserved and we have the important property that the value d[i]of d at vertex qiin the computer implementation of d by an array of values at the nodes,satisfies

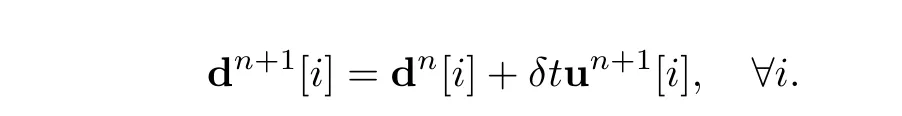
In other words,dn◦Yn+1is dn[i]after moving the vertices by(3.9).

4 Energy Estimate

4.1 Stability of the scheme discretised in time

To conserve energy we need to change the scheme(3.8)slightly,from

4.2 Energy estimate for the fully discrete scheme

The proof for the spatially continuous case will work for the discrete case if

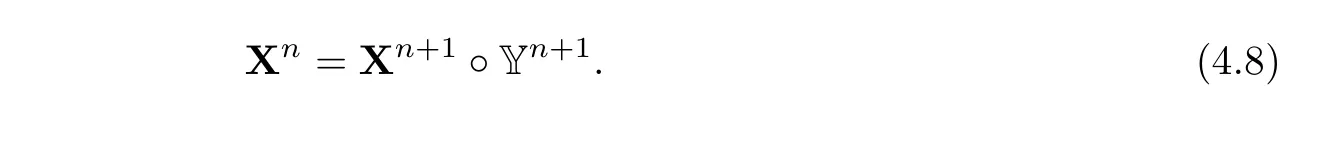
Figure 2 Sketch to understand if Xn=Yn+1◦Xn+1holds with the P1−P1 stabilised element.A triangle in the reference domain(chosen here to be its initial position at time zero)becomes triangleat tnandat time tn+1:=Xn()and=Xn+1(),respectively.Vertices are preserved by these transformations.

As discussed in[19]it may be possible to program an isoparametric P2−P1element for which(4.8)but it is certainly far from easy.On the other hand,consider the stabilised P1−P1element:Thefluid pressure and the solid pressure are continuous and piecewise linear on the triangulation.The inf-sup condition for stability does not hold unless the incompressibility condition in thefluid,∇·u=0,is changed to−αΔp+∇·u=0.In[4],for instance,more details are given explaining why α should be proportional to h2,in 2D,h being the local size of the mesh edges.It amounts to adding α∇pn+1·∇^p next to the term with µfin the variational formulations.Then(4.8)holds(see Figure 2)and the proof of the spatially continuous case can be adapted leading to(4.7)with an additional viscous term ∈|∇pn+1|2next to the term withµf.

Remark 4.1Because of energy preservation scheme(4.1),implemented via afixed point algorithm as in(3.7),generates bounded sequences ρ,u,qi;it seems safe to assess that out of these bounded subsequences will converge to a solution of the problem discretised in space but continuous in time when δt→ 0.

5 Numerical Tests

In our tests we have used the P2−P1element with 2 iterations for the nonlinear system at each time step.In most cases 3 iterations are unnecessary but one iteration is not enough.At each iteration the linear system is solved with the library MUMPS—implemented in FreeFem++(see[18])—and the condition number does not seem to be an issue,which is natural since the main contribution to the matrix is the mass matrix.Although mathematically better the stabilised P1−P1element with α =10−4did not perform better.For instance,on FLUSTRUKFSI-2∗below,theflag touches,correctly,the bottom boundary at 0.41 when a mesh with 9568 vertices is used and does not converge with a mesh of 2511 vertices.

We have also tested the effect of adding the term of order δt2to the nonlinear system:It made no visible differences.

5.1 The cylinder-flag test

A compressible hyperelastic Mooney-Rivlin material,shaped as a rectangle of size[0,l]×[0,h],is attached behind a cylinder of radius r and beats in tune with the Karman vortices of the wake behind the cylinder;thefluid in the computational rectangular domain[0,L]×[0,H]enters from the left and is free to leave on the right.The center of the cylinder is at(c,c)(see Figure 1).In[13]the following numerical values are suggested.

Geometryl=0.35,h=0.02,L=2.5,H=0.41,c=0.2 which puts the cylinder slightly below the symmetry line.

Fluiddensity ρf=103horizontal velocity u(0,y)=is a parabolic profile with flux UH.Top and bottom boundaries are walls with no-slip conditions.

SolidE=2µ(1+ σ),σ =0.4,λ =

Initial velocities and displacements are zero.In all cases the same mesh is used initially with 2511 vertices.The time step is 0.005.

5.1.1 Free fall of a thickflag

The gravity is g=9.81 in Ωt.When U=0,µ =1.5106and ρs=20ρf,the flag falls under its own weight;it comes to touch the lower boundary with zero velocity at time 0.4 and then moves up under its spring effect.This test is named FLUSTRUK-FSI-2∗in[13]but we have used a different value for µ because the one reported in[13]does not give the value used for the gravity.

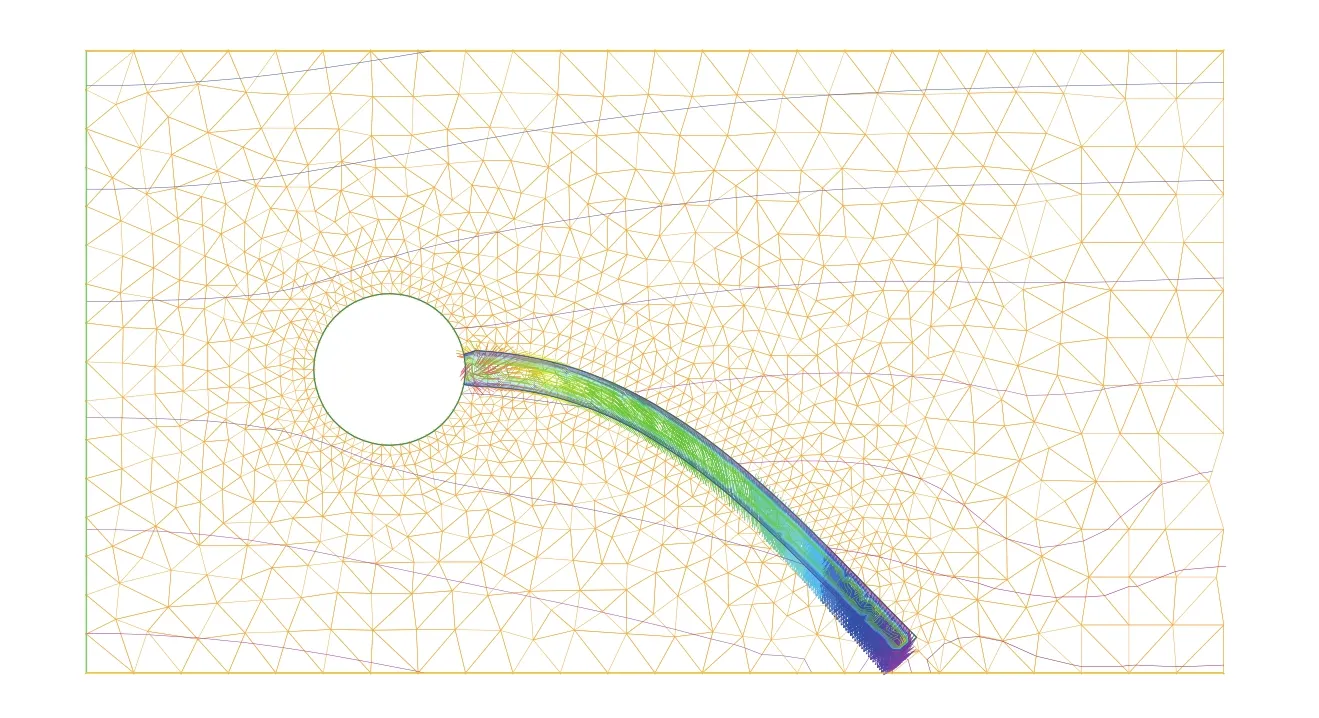
Figure 3 FLUSTRUK-FSI-2∗(see[13]).Zoom near theflag at t=0.4 just as it begins to move up after the fall under its own weight in aflow initially at rest.Mesh and Pressure lines are shown in thefluid and velocity vectors in the solid.

Figure 3 shows a zoom around theflag at the time when it has stopped to descend and started to move upward.Pressure lines are drawn in theflow region together with the mesh and the velocity vectors in theflag and drawn at each vertex.Figure 4 shows the coordinates of the upper right tip of theflag versus time.It shows also that mass is conserved because the integral in the solid of Jh is plotted.Finally to check the stability of the algorithm for high values of ρswe performed the same test but with ρs=2106and µs=2.5106(with 1.5 instead of 2.5 the flag touches the bottom boundary).Then we compared with ρs=2 for the same value ofµs.Results are shown in Figure 5.Stability is established and a high value of ρsaffects the frequency of the oscillations.

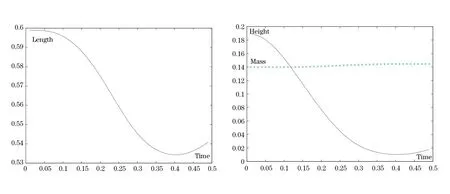
Figure 4 FLUSTRUK-FSI-2∗test of[13].Position of the upper right corner of theflag versus time:x vs t on the left and y vs t on the right.In addition on the right the mass multiplied by 20 is plotted at each time step.

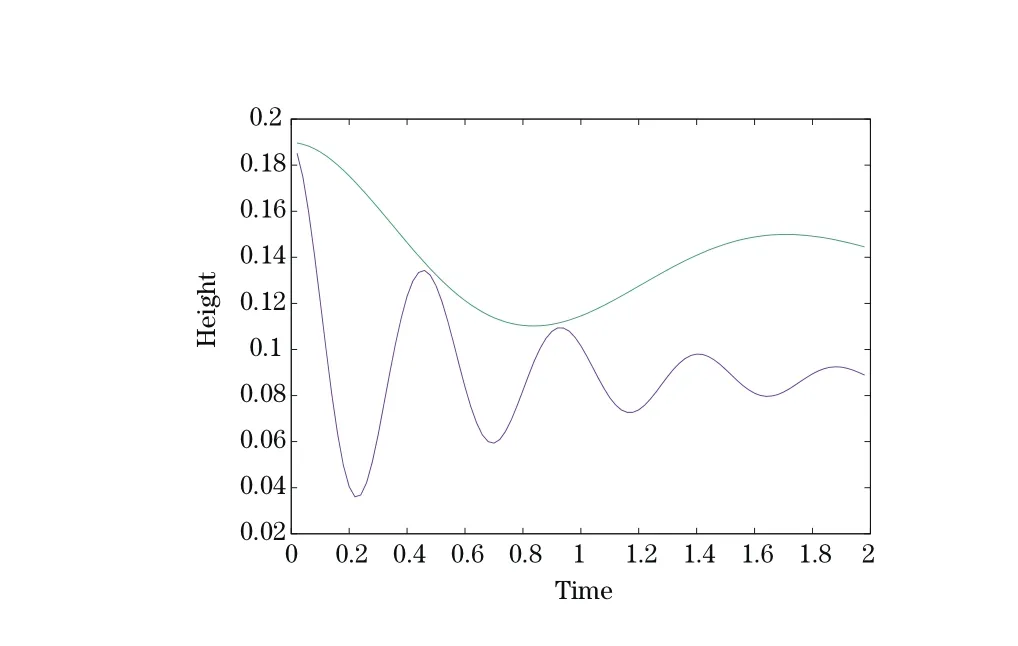
Figure 5 FLUSTRUK-FSI-2∗: µs=2.5106;comparison between a small value of ρs=2(top curve),and a high value ρs=2106(lower curve).

5.1.2 Flow past a cylinder with a thickflag attached

This test is known as FLUSTRUK-FSI-3 in[13].The geometry is the same as above but now U=2,µ =2106and ρs= ρf.After some time a Karman-Vortex alley develops and theflag beats accordingly.Results are shown in Figures 6—7;the first one displays a snapshot of the velocity vector norms and the second the y-coordinate versus time of the top right corner of theflag.

These numerical results compare reasonably well with those of[13].The frequency is 5s−1compared to 5.04 and the maximum amplitude 0.031 compared to 0.032.However the results are still somewhat sensitive to the time step size,the number of iterations in the nonlinear solver and the mesh size.An extensive convergence analysis needs to be made to assert that the precision of these simulations is better than 10%.

Figure 6 FLUSTRUK-FSI-3 Test.Color map based on the norm of thefluid and solid velocity vectors.

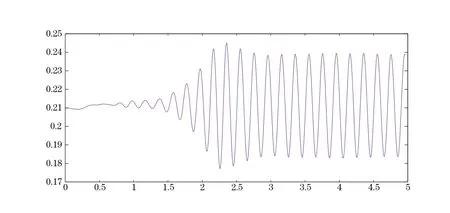
Figure 7 FLUSTRUK-FSI-3 Test.Vertical position of the upper right tip of theflag versus time shown up to t=5.

6 Conclusion

A fully Eulerianfluid-structure formulation has been presented for compressible materials with large displacements,discretised by an implicitfirst order Euler Scheme and the P2−P1or stabilised P1−P1elements.An energy estimate has been obtained which guarantees the stability of the scheme so long as the motion of the vertices does notflip-over a triangle.The method has been implemented with FreeFem++(see[18]).It is reasonably robust when the vertices in the structure are moved by their velocities and thefluid is remeshed with an automatic Delaunay mesh generator.The method isfirst order in time and therefore somewhat too diffusive for delicate tests.It is being extended to 3D and to second order in time discretisation.

7 Appendix

7.1 The Freefem++Script

We include this script for readers wishing to try the program.First download and install FreeFEM++and then run this program.

AcknowledgementThe author thanks Fr´ed´eric Hecht for very valuable discussions and comments.

[1]Antman,S.S.,Nonlinear Problems of Elasticity,(2nd ed.),Applied Mathematical Sciences,107,Springer-Verlag,New York,2005.

[2]Bathe,K.J.,Finite Element Procedures,Prentice-Hall,Englewood Cliffs,NJ,1996.

[3]Bathe,K.J.,Ramm,E.and Wilson,E.L.,Finite element formulations for large deformation dynamic analysis,Int.J.Numer.Methods Eng.,9(2),1975,353–386.

[4]Boffi,D.,Brezzi,F.and Fortin,M.,Mixed Finite Element Methods and Applications,Computational Mathematics,Heidelberg,44,Springer-Verlag,Berlin,2013.

[5]Boffi,D.,Cavallini,N.and Gastaldi,L.,The finite element immersed boundary method with distributed Lagrange multiplier,SIAM J.Numer.Anal.,53(6),2015,2584–2604.

[6]Boulakia,M.,Existence of weak solutions for the motion of an elastic structure in an incompressible viscousfluid,C.R.Math.Acad.Sci.Paris,336(12),2003,985–990.

[7]Bukaca,M.,Canic,S.,Glowinski,R.,et al.,Fluid-structure interaction in bloodflow capturing non-zero longitudinal structure displacement,Journal of Computational Physics,235,2013,515–541.

[8]Chiang,C.-Y.,Pironneau,O.,Sheu,T.and Thiriet,M.,Numerical study of a 3D Eulerian monolithic formulation forfluid-structure-interaction,Fluids,2017.

[9]Ciarlet,P.G.,Mathematical Elasticity,I.,Three-dimensional Elasticity,North Holland,Amsterdam,1988.

[10]Cottet,G.H.,Maitre,E.and Milcent,T.,Eulerian formulation and level set models for incompressiblefluid-structure interaction,M2AN Math.Model.Numer.Anal.,42(3),2008,471–492.

[11]Coupez,T.,Silva,L.and Hachem,E.,Implicit Boundary and Adaptive Anisotropic Meshes,New challenges in Grid Generation and Adaptivity for Scientific Computing,S.Peretto and L.Formaggia(eds.),5,Springer-Verlag,Cham,2015.

[12]Coutand,D.and Shkoller,S.,Motion of an elastic solid inside an incompressible viscousfluid,Arch.Ration.Mech.Anal.,176(1),2005,25–102.

[13]Dunne,T.,Adaptive finite element approximation offluid-structure interaction based on an Eulerian variational formulation,ECCOMAS CFD,2006,Wesseling,P.,O˜nate,E.and P´eriaux,J.(eds.),Elsevier,TU Delft,The Netherlands,2006.

[14]Dunne,T.,An Eulerian approach tofluid-structure interaction and goal-oriented mesh adaptation,Int.J.Numer.Meth.Fluids,51,2006,1017–1039.

[15]Dunne,Th.and Rannacher,R.Adaptive Finite Element Approximation of Fluid-Structure Interaction Based on an Eulerian Variational Formulation,Fluid-Structure Interaction:Modelling,Simulation,Optimization,Bungartz,H-J.and Schaefer,M.(eds.),Lecture Notes in Computational Science and Engineering,53,Springer-Verlag,Berlin,2006,110–146.

[16]Fernandez,M.A.,Mullaert,J.and Vidrascu,M.,Explicit Robin-Neumann schemes for the coupling of incompressiblefluids with thin-walled structures,Comp.Methods in Applied Mech.and Engg.,267,2013,566–593.

[17]Formaggia,L.,Quarteroni,A.and Veneziani,A.,Alessandro Multiscale Models of the Vascular System,Cardiovasuclar Mathematics,Springer-Verlag,Italia,Milan,2009,395–446.

[18]Hecht,F.,New development in FreeFem++,J.Numer.Math.,20,2012,251–265,http://www.FreeFem.org.

[19]Hecht,F.and Pironneau,O.,An energy stable monolithic Eulerian fluid-structurefinite element method,International Journal for Numerical Methods in Fluids,85(7),2017,430–446.

[20]Change Heil,Matthias to Heil,M.,Solvers for large-displacementfluid structure interaction problems:Segregated versus monolithic approaches,Comput.Mech.,43,2008,91–101.

[21]Hron,J.and Turek,S.,A monolithic fem solver for an ALE formulation offluid-structure interaction with configuration for numerical benchmarking,European Conference on Computational Fluid Dynamics ECCOMAS CFD,2006,Wesseling,P.,Onate,E.and Periaux,J.(eds.),TU Delft,The Netherlands,2006.

[22]L´eger,S.,M´ethodelagrangienne actualis´ee pour desprobl`emes hyper´elastiquesen tr`es grandes d´eformations,Th`ese de Doctorat,Universit´e Laval,2014(in France).

[23]Le Tallec,P.and Hauret,P.,Energy conservation in Fluid-Structure Interactions,Numerical Methods for Scientific Computing,Variational Problems And Applications,Neittanmaki,P.,Kuznetsov,Y.and Pironneau,O.(eds.),CIMNE,Barcelona,2003.

[24]Le Tallec,P.and Mouro,J.,Fluid structure interaction with large structural displacements,Comp.Meth.Appl.Mech.Eng.,190(24–25),2001,3039–3068.

[25]Liu,J.,A second-order changing-connectivity ALE scheme and its application to FSI with large convection offluids and near-contact of structures,Journal of Computational Physics,304,2016,380–423.

[26]Liu,I-Shih,Cipolatti,R.and Rincon,M.A.,Incremental Linear Approximation for Finite Elasticity,Proc.ICNAAM,Wiley,2006.

[27]Marsden,J.and Hughes,T.J.R.,Mathematical Foundations of Elasticity,Dover Publications,New York,1994.

[28]Nobile,F.and Vergara,C.,An effective fluid-structure interaction formulation for vascular dynamics by generalized Robin conditions,SIAM J.Sci.Comp.,30(2),2008,731–763.

[29]Peskin,C.S.,The immersed boundary method,Acta Numerica,11,2002,479–517.

[30]Pironneau,O.,Numerical Study of a Monolithic Fluid-Structure Formulation,Variational Analysis and Aerospace Engineering,116,Springer-Verlag,Cham,2016.

[31]Rannacher,R.and Richter,T.,An Adaptive Finite Element Method for Fluid-Structure Interaction Problems Based on a Fully Eulerian Formulation,Lecture Notes in Computational Science and Engineering,73,Springer-Verlag,Heidelberg,2010.

[32]Raymond,J.-P.and Vanninathan,M.,Afluid-structure model coupling the Navier-Stokes equations and the Lam´e system,J.Math.Pures Appl.,102,2014,546–596.

[33]Richter,Th.and Wick,Th.,Finite elements forfluid-structure interaction in ALE and fully Eulerian coordinates,Comput.Methods Appl.Mech.Engrg.,199,2010,2633–2642.

[34]Wang,Y.X.,The Accurate and Efficient Numerical Simulation of General Fluid Structure Interaction:A Unified Finite Element Method,Proc.Conf.on FSI problems,IMS-NUS,Singapore,2016.