Poincar´e’s Lemma on Some Non-Euclidean Structures

Alexandru KRISTÁLY

(Dedicated to Philippe G.Ciarlet on the occasion of his 80th birthday)

1 Introduction and Main Result

Let Ω ⊆ Rnbe an open,simply connected set,and a=(ai)∈ C1(Ω;Rn),n ≥ 2.The classical Poincar´e lemma says that there exists u ∈ C2(Ω)with

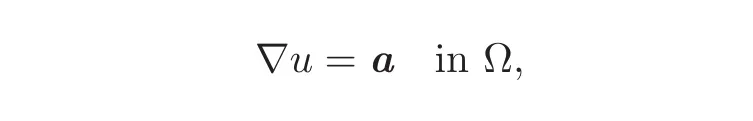
if and only if curl a=0 in C(Ω;Rn),i.e.,

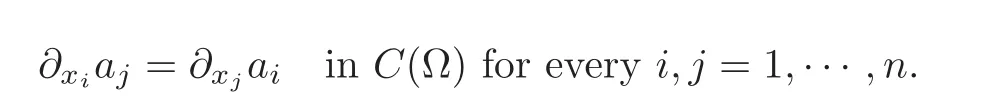
Here,as usual, ∇u=(∂xiu) ∈ C1(Ω;Rn).For a weak version of the Poincar´e lemma(e.g.in L2(Ω))and its equivalent formulation in terms of fundamental results in the theory of PDEs,we refer the reader to Amrouche,Ciarlet and Mardare[3—4]and to the comprehensive monograph by Ciarlet[12,Chapter 6].

Very recently,Poincar´e’s lemma has been extended to some specific low-dimensional sub-Riemannian structures with rank 2 distributions;e.g.,thefirst Heisenberg group H1,Engel-type manifolds,Grushin and Martinet type distributions,and the sub-Riemannian 3-dimensional sphere S3(see Calin,Chang and Eastwood[6—7]and Calin,Chang and Hu[8—10]).In the sub-Riemannian setting,the number of equations in the system which is going to be solved is strictly less than the space dimension.Accordingly,the solvability of such gradient-type systems deeply depends on the Lie bracket generating properties of the sub-Riemannian distributions,and it turns out that the “curl-vanishing” characterization of the solvability of the sub-Riemannian system becomes a system of PDEs containing higher-order derivatives.In order to visualize this phenomenon,we consider thefirst Heisenberg group H1=C×R endowed with its usual group operation and left-invariant vectorfields X1= ∂x1−2x2∂x3and X2= ∂x2+2x1∂x3.The sub-Riemannian system

is solvable in F(H1)(=the space of smooth functions on H1)for a=(a1,a2)∈C1(H1;R2)if and only if

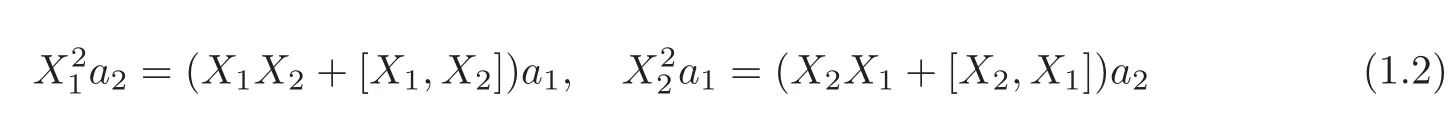
(see,e.g.Calin and Chang[5,Theorem 2.9.8]).In addition,the solution u of(1.1)can be given the work done by the force vectorfield X=a1X1+a2X2along any horizontal curve starting from 0∈H1,called also as the Ces`aro-Volterra horizontal path integral.

The purpose of our paper is to prove Poincar´e lemmas on some sub-Riemannian structures of arbitrary dimension with corank 1 distribution,including for instance step-two Carnot groups with not necessarily trivial kernel.In the sequel,we present our main result(see Section 3 for the notions used below).

Let(M,D,g)be an(n+1)-dimensional sub-Riemannian manifold(n≥2),and consider the distribution D in a given local coordinate system(xi)i=1,···,n+1containing vector fields of the form

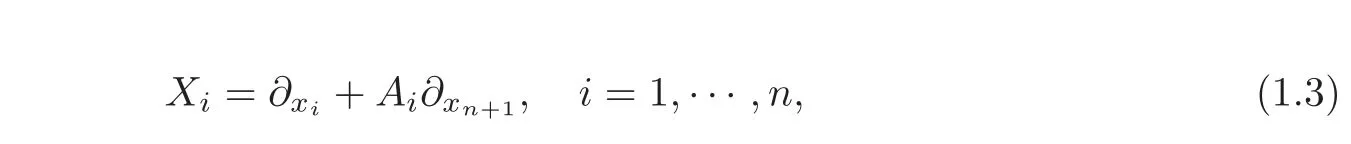
where Ai:M → R are smooth functions depending only on thefirst n variables,i.e.,Ai=Ai(x1,···,xn).We assume that

and

Due to the latter assumptions,the rank n distribution D is nonholonomic on M,since

Given a∈ Γ(D)(=the set of horizontal vectorfields on M),we are going to study the solvability of the system

where u ∈ F(M)and ∇Hdenotes the horizontal gradient.Our main result,the Poincar´e lemma on sub-Riemannian manifolds,reads as follows.

Theorem 1.1Let(M,D,g)be an(n+1)-dimensional simply connected sub-Riemannian manifold(n≥ 2),where the distributionDis given by the vectorfields in(1.3)with functionsAidepending only on thefirstnvariables,verifying(1.4)andI0/= Ø.

Givena∈Γ(D),the sub-Riemannian system(1.6)has a solutionu∈F(M)if and only if

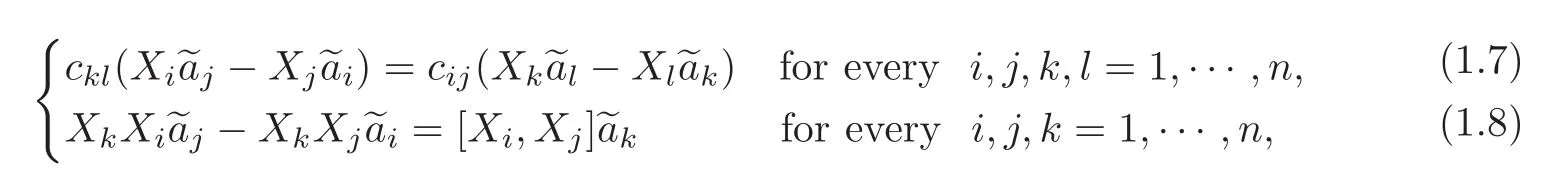
wherea=aiXiand=gijai(the summations being from1ton),and(gij)are the components ofgwith respect to the distributionD.Moreover,ifx0∈M,the solutionu:M→Rfor the system(1.6)can be obtained by

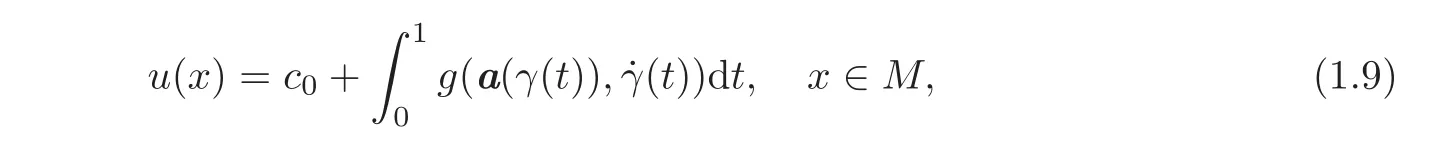
wherec0=u(x0)∈ Randγ :[0,1]→ Mis any horizontal curve joiningx0withx.

Some remarks are in order.

Remark 1.1(a)Although(1.7)and(1.8)contain n4and n3conditions,a simple combinatorial reasoning shows that it is enough to verify at most

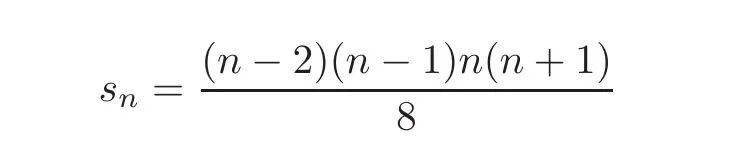
and

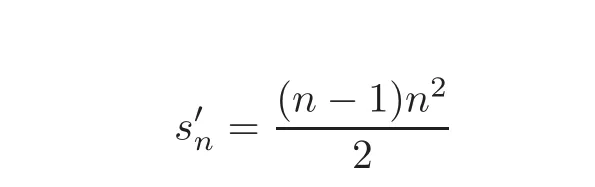
conditions,respectively.Thus,the number of compatibility conditions is

(b)Theorem 1.1 provides an answer to the open question of Calin and Chang[5,p.55]whenever the sub-Riemannian manifold with arbitrarily dimension has corank 1 distribution.We note that the existing results in the literature solve the system(1.6)only for two components,i.e.,the distributions contain two vectorfields.In particular,if M=H1is thefirst Heisenberg group,the solvability of the system(1.1)can be recovered by Theorem 1.1;indeed,in this particular case,n=2,D={X1,X2}and gij= δij.Moreover,A1= −2x2,A2=2x1;thus c12= −c21=4 and c11=c22=0 in(1.4).Notice that thefirst-ordered relations in(1.7)are trivially satisfied(supported also by the fact that s2=0,thus nothing should be checked),while the second-ordered ones(1.8)reduce precisely to(1.2),containing=2 conditions.In higherdimensional Heisenberg groups Hd,d≥ 2,thefirst-ordered assumptions are indispensable as well.

(c)There are more involved,non-Heisenberg-type vectorfields which verify also the assumptions of Theorem 1.1.Indeed,let(R5,D,g)be the sub-Riemannian manifold with the vectorfields Xi,i=1,···,4 from(1.3)with A1=In this case we have that the elements from(1.4)are c12=4=−c21,c34=2=−c43,while the rest of cij’s are zero.

(d)Note that Theorem 1.1 can be formulated on any simply connected open domain instead of the whole M.

Organization of the paperIn Section 2 we prove the Poincar´e lemma on generic Riemannian manifolds.As a direct byproduct,we also state a Saint-Venant lemma on Riemannian manifolds whose proof is presented in the Appendix(Section 6).The Poincar´e lemma on generic Riemannian manifolds turns to be indispensable in the proof of our main theorem,which will be provided in Section 3.Here,we shall explore basic properties of the Riemannian manifolds as the metric compatibility and torsion-freeness(or symmetry)of the Levi-Civita connection with respect to the Riemannian metric.In fact,we shall reduce our original sub-Riemannian system(defined on the distribution)to a differential system on a Riemannian manifold where we can apply the Riemannian Poincar´e lemma and Ces`aro-Volterra integral formula.An elegant computation connects the force vectorfields in these two settings,proving in this way relation(1.9).In Section 4 we give some examples,thefirst on the hyperbolic spaces,the second one on Carnot/Heisenberg groups.In Section 5 we formulate some problems for further investigations.

2 Poincar´e Lemma on Riemannian Manifolds:A Local Version

Let(M,g)be an m-dimensional Riemannian manifold;here(gij)are the components of the Riemannian metric g in a given local coordinate system(xi)i=1,···,m.

Let u:M → R be a C1-functional on M;the differential of u at x,denoted by du(x),belongs to the cotangent spaceM and is defined by

in the sequel,we prefer to use 〈·,·〉ginstead of g.If the local components of du are denoted by uk= ∂xku,then the local components of∇gu are ui=gikuk;here,gijare the local components of g−1=(gij)−1.

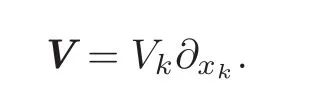
The main result of the present section is the Poincar´e lemma on Riemannian manifolds.

Theorem 2.1Let(M,g)be anm-dimensional Riemannian manifold andΩ⊆Mbe a simply connected open set.Given a vectorfieldV ∈ C1(Ω,TΩ),the system

is solvable inC2(Ω)if and only if we have

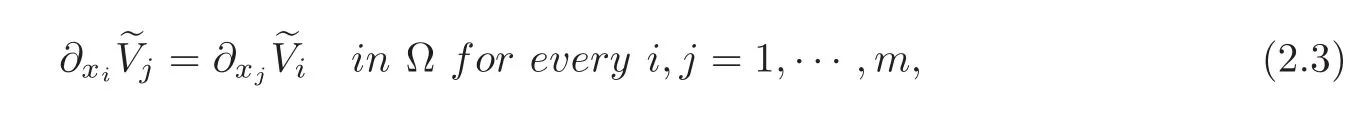
where

Moreover,ifx0∈Ωisfixed and(2.3)holds,the solutionu:Ω→Rfor(2.2)can be obtained by

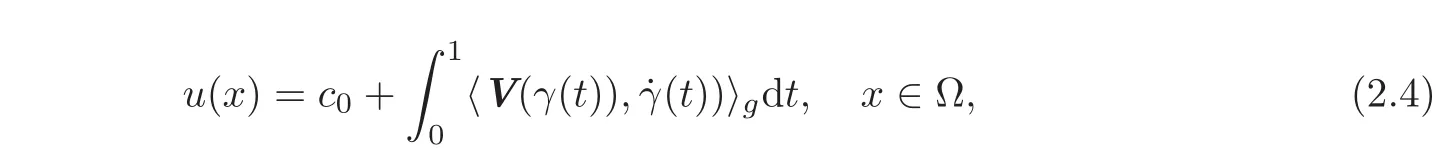
wherec0=u(x0)∈ Randγ :[0,1]→ Ωis any curve joiningx0withx.

Proof(2.2)⇒(2.3).First of all,(2.2)is equivalent to

Multiplying both sides by gji,we have

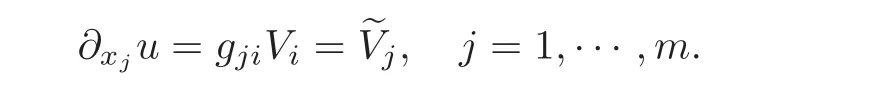
Deriving these relations,(2.3)yields at once by the symmetry of second-order derivatives.

(2.3)⇒(2.2).We closely follow the proof from Ciarlet[12,Theorem 6.17-2].Let x0∈ Ωbe given and fix x ∈ Ω.Since Ω is simply connected,there exists a path γ :[0,1]→ Ω such that γ(0)=x0and γ(1)=x.If there exists u ∈ C2(Ω)which satisfies(2.2),then the function P:[0,1]→ R defined by P(t)=u(γ(t))verifies

The latter equation together with the Cauchy data P(0)=P0∈R provides a unique solution P:[0,1]→ R which depends on the path γ.

We are going to show that the value P(1)does not depend on the choice of the path γ whenever(2.3)holds.To see this,let γ0,γ1:[0,1] → Ω be two smooth paths such that γi(0)=x0and γi(1)=x,i ∈ {0,1}.Since Ω is simply connected,we can find a smooth homotopy H:[0,1]× [0,1]→ Ω between γ0and γ1,i.e.,

For every λ ∈ [0,1],let P(·,λ):[0,1]→ R be the unique solution of the Cauchy problem

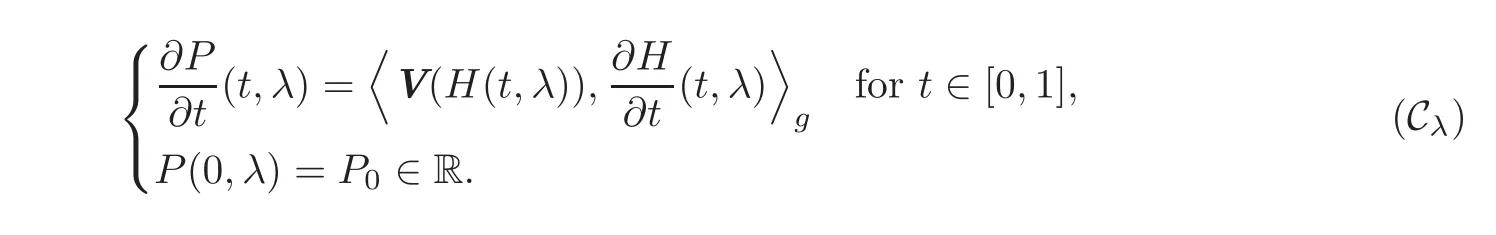
We claim that

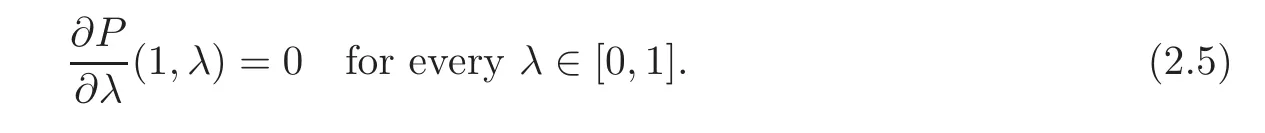
To see this,let us consider the function σ :[0,1]× [0,1]→ R defined by

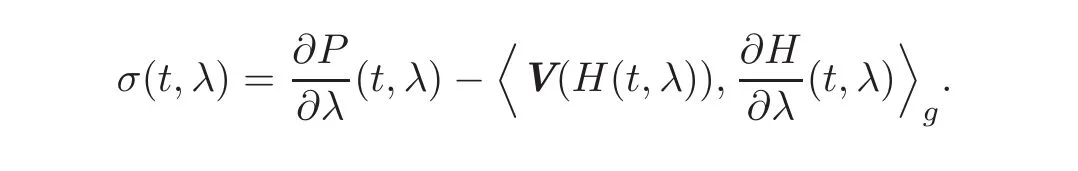
Since the Levi-Civita connection is compatible with the Riemannian metric,it follows from[16,Proposition 3.2]that

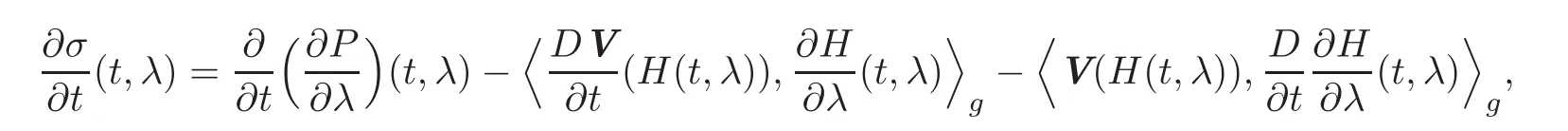
where D denotes the covariant derivation on(M,g).Concerning the latter term,we know from the torsion-freeness of the Levi-Civita connection on(M,g)that

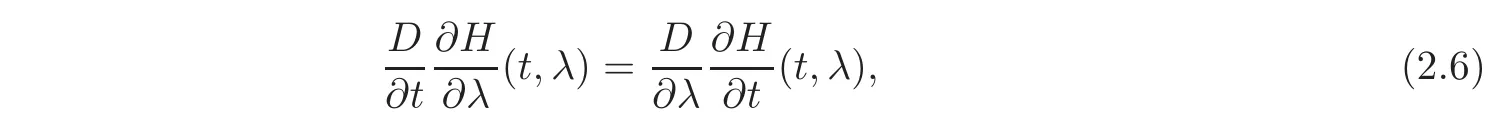
(see[16,Lemma 3.4]).The sophisticated part is to show that

To prove(2.7)we recall the following well-known facts:If W=(w1,···,wm)is a vector field along a path(x),its covariant derivative can be expressed by

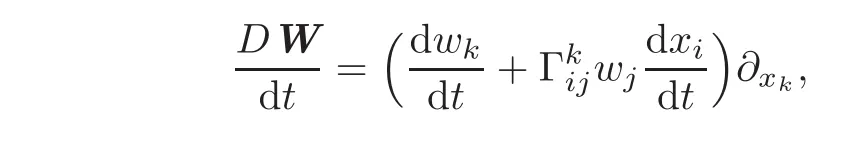
Coming back to(2.7),we have

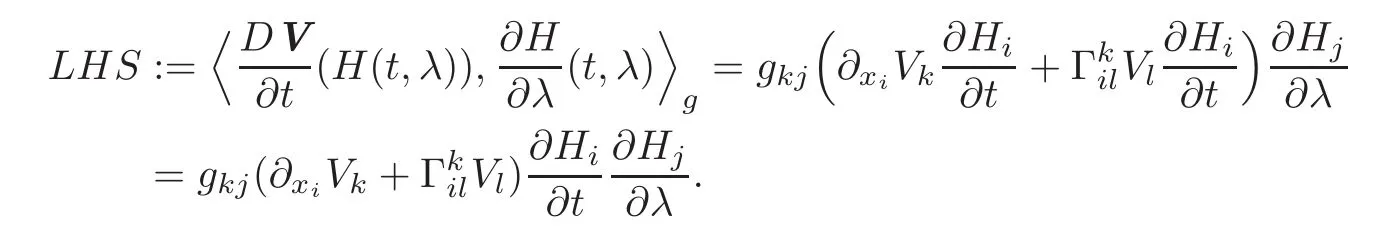
In a similar way,

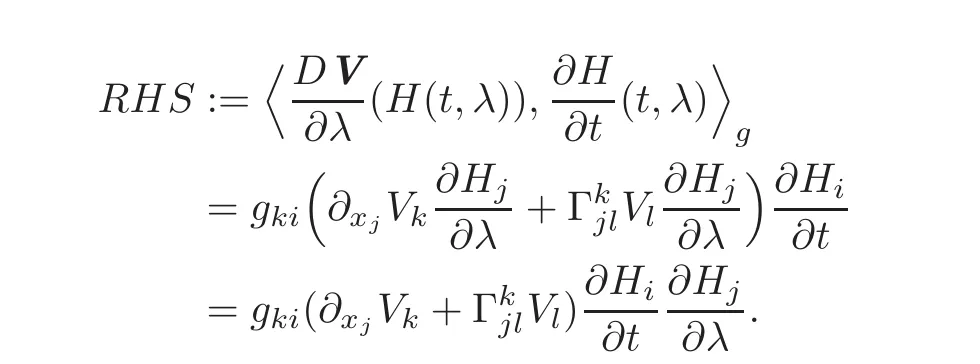
Therefore,we have that

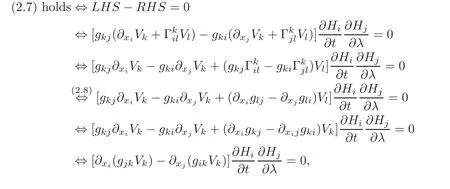
where the latter relation holds true due to(2.3).Consequently,by relations(2.6)—(2.7)and the Cauchy problem(Cλ)we have

i.e.,t → σ(t,λ)is constant.Since P(0,λ)=P0∈ R and H(0,λ)=x0,it turns out that

In particular,

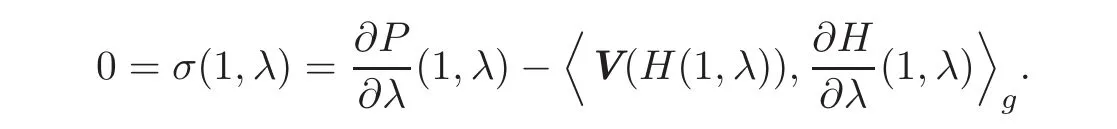
Since H(1,λ)=x0for every λ ∈ [0,1],it follows the claim(2.5),showing that the value P(1)is not depending on the particular choice of the path.

For every x∈ Ω,let u:Ω → R be defined by

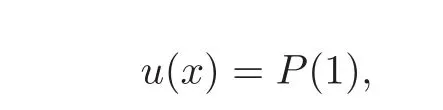
where P is the unique solution to the Cauchy problem(Cλ)having the initial data P(0)=P0and using any path joining x0and x;thus,the function u is well-defined.

To conclude the proof,we show the validity of(2.2).Let x∈Ω and v∈TxM be arbitrarilyfixed elements.Let γ:[0,1]→Ω be a path such that γ(0)=x0,γ(1)=x and˙γ(1)=v∈TxM,and let P be the solution of the Cauchy problem associated to this path,thus,P(t)=u(γ(t)).Therefore,the latter relation yields that

On the other hand,by the Cauchy problem we have

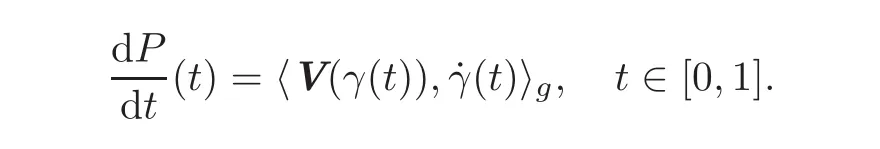
Accordingly,for the moment t=1,it follows that

and the arbitrariness of v∈TxM concludes the proof of(2.2).

If γ :[0,1]→ Ω is any path joining the points x0and x,the Ces`aro-Volterra path integral formula easily follows as

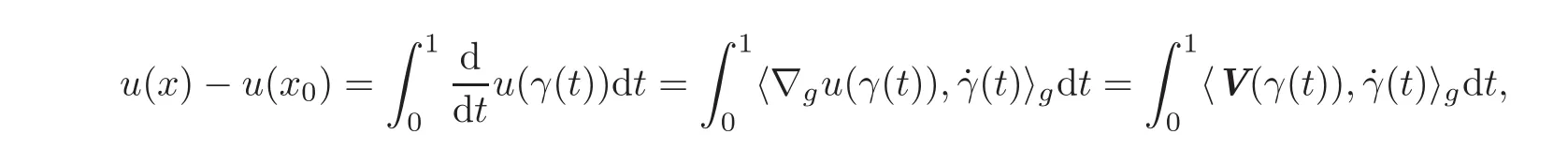
which is precisely(2.4).

Remark 2.1Poincar´e’s lemma can be also proved by using 1-forms,see,e.g.Abraham,Marsden and Ratiu[1].However,we preferred here a direct proof based on local coordinates for two reasons:(a)It highlights the importance of the Riemannian structure,i.e.,the metric compatibility and torsion-freeness of the Levi-Civita connection,which is not valid anymore on non-Riemannian Finsler settings(see Section 5 for details);(b)The proof provides directly a Ces`aro-Volterra path integral formula.

As a byproduct of the Poincar´e lemma(Theorem 2.1),we state a Saint-Venant lemma on generic Riemannian manifolds;its proof is sketched in the Appendix.To present it,fix ei∈ TΩ,i=1,···,m,and assume that they can be represented as

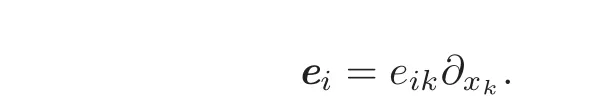
The m-vectorfield e=(e1,···,em)∈ C2(Ω,TΩm)is called symmetric if eij=eji∈ C2(Ω)for every i,j=1,···,m.

Proposition 2.1Let(M,g)be anm-dimensional Riemannian manifold andΩ⊆Mbe a simply connected open set.Givene=(e1,···,em)∈ C2(Ω,TΩm)a symmetricm-vectorfield onΩ,the system

has a vectorfield solutionV=(V1,···,Vm) ∈ C3(Ω,Rm),where the components of the symmetric gradient∇s,gVare given by

if and only if the Saint-Venant compatibility relations hold(in local coordinate system)inΩ,i.e.,

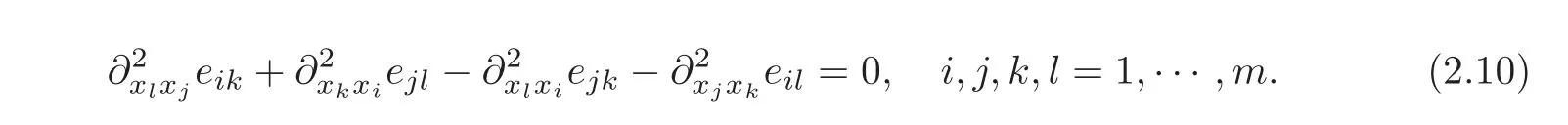
Moreover,ifx0∈Misfixed and(2.10)holds,then the solution of(2.9)is obtained by

where

withUi=gls(pis+eis)∂xl,

andWij=gls(∂xjeis− ∂xiejs)∂xlfor some numbersand the curveγ :[0,1]→ Ωisarbitraryfixed joiningx0withx∈Ω.

Remark 2.2(a)Note that∇s,gV is a kind ofsymmetric Lie derivativeof the vectorfield V with respect to the Riemannian metric g;indeed,the latter notion appears in[11,p.518],where∇s,gV is an L−type tensor of the form

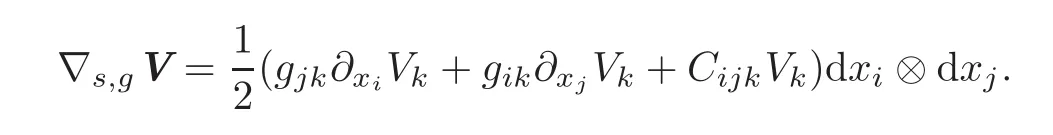
In our setting,the elements Cijkare expressed by means of the Christoffel symbols as

(b)Proposition 2.1 provides a curved version of the Saint-Venant lemma;further curvilinear versions of the Saint-Venant lemma can be found in the papers by Ciarlet,Gratie,Mardare and Shen[13],Ciarlet and Mardare[14],and Ciarlet,Mardare and Shen[15].

3 Proof of Theorem 1.1

In order to prove Theorem 1.1,wefirst recall some basic notions from the theory of sub-Riemannian manifolds;for further details,see Agrachev,Barilari and Boscain[2],Calin and Chang[5]and Figalli and Rifford[17].

Let M be a smooth connected(n+1)-dimensional manifold(n≥2),D be a smooth nonholonomic distribution of rank m≤n on M(i.e.,a rank m subbundle of the tangent bundle TM)and g be a Riemannian metric on D.Without loss of generality,we may assume that g is defined on the whole tangent bundle TM(not necessarily in a unique way);we shall keep the same notation of g on TM.The triplet(M,D,g)is a sub-Riemannian manifold.As usual,the distribution D is said to be nonholonomic if for every x∈M there exists an m-tuple,···,of smooth vector fields on a neighborhood Nxof x such that all the Lie brackets generated by these vectors at y generate TyM for every y ∈ Nx.A curve γ :[0,1]→ M is horizontal with respect to D if it belongs to W1,2([0,1];M)and˙γ(t)∈D(γ(t))for a.e.t∈[0,1].If D is nonholonomic on M,by the Chow-Rashewsky theorem,every two points of M can be joined by a horizontal path.Let Γ(D)be the set of horizontal vector fields on M,and F(M)be the set of smooth functions on M.If u∈F(M),the horizontal gradient∇Hu∈Γ(D)of u is defined by g(∇Hu,X)=X(u)for every X ∈ Γ(D).

Now,let us put ourselves into the context of Theorem 1.1.Accordingly,let(M,D,g)be an(n+1)-dimensional sub-Riemannian manifold(n≥2),and the rank n distribution D in a local coordinate system(xi)i=1,···,n+1formed by the vector fields given in(1.3)and verifying(1.4).Since

by(1.4)we obtain(1.5),i.e.,

[Xi,Xj]=XiXj− XjXi=(∂xiAj− ∂xiAj)∂xn+1=cij∂xn+1for every i,j=1,···,n.Therefore,since I0={(i,j):cij/=0}/=Ø,the distribution D is nonholonomic on M.

Let a∈Γ(D)befixed.The system(1.6),i.e.,

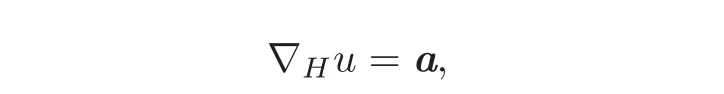
in local coordinates reads as

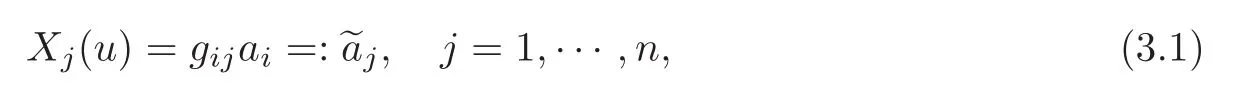
where gij=g(Xi,Xj)and a=aiXi.With this preparatory part in our mind,we now present the proof of our main result.

Proof of Theorem 1.1(1.6)⇒(1.7)—(1.8).Assume that the sub-Riemannian system(1.6)has a solution u∈F(M).First,by(1.5)applied to u,we have

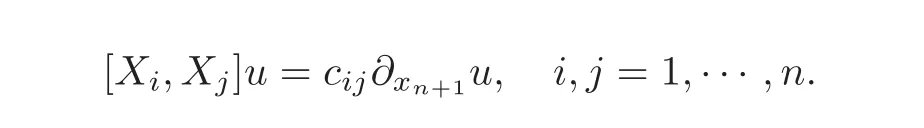
This relation and(3.1)give that

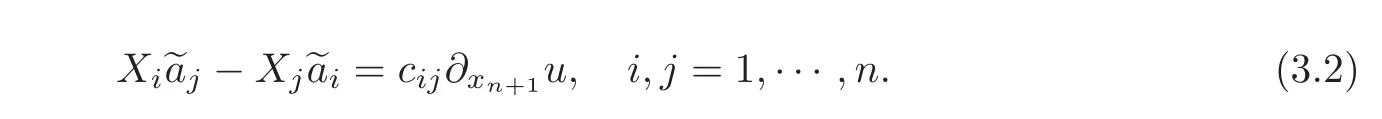
If∂xn+1u(x)=0 for some x ∈ M,then=0 for every i,j=1,···,n,thus(1.7)clearly holds.If∂xn+1u(x)/=0 for some x∈ M,then by writing the relation(3.2)for(k,l)instead of(i,j),and eliminating∂xn+1u(x)/=0,we obtain(1.7).

Deriving(3.2)with respect to the vector field Xk,k=1,···,n,and taking into account that[Xk,∂xn+1]=Xk∂xn+1− ∂xn+1Xk=0,it turns out by(3.1)and(1.5)that

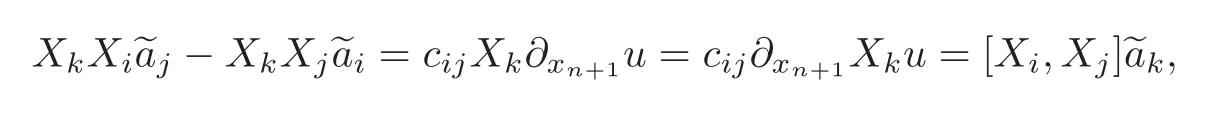
which is precisely relation(1.8).

(1.7)—(1.8)⇒(1.6).Since I0/= Ø,let(i0,j0)∈ I0and introduce the function

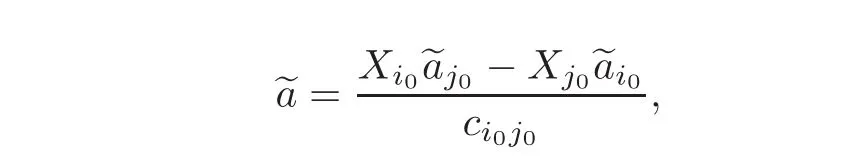
Let

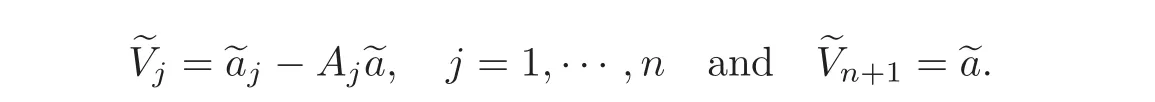
We are going to prove that

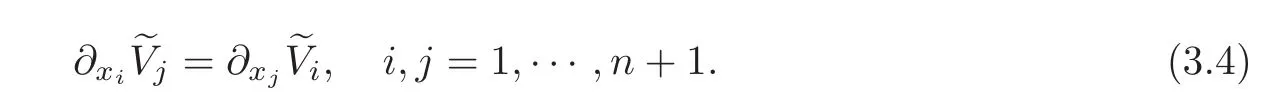
To do this,we distinguish three cases:

Case 1i=j=n+1.(3.4)trivially holds.

Case 2i∈ {1,···,n}and j=n+1.On one hand,(3.4)is equivalent to ∂xiOn the other hand,by the definition of~a,(1.8)and(1.5)we have that

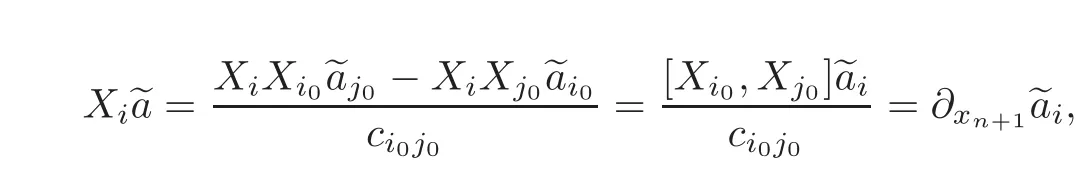
which is the required relation.

Case 3i,j ∈ {1,···,n}.We have the following chain of equivalences:

By the definition of~a,let us observe that the latter relation is nothing but(1.7)with the choice(k,l)=(i0,j0),which concludes the proof of(3.4).

According to Theorem 2.1(applied forand relation(3.4),it turns out that the system(3.3)has a solution in C2(M),which can be obtained by

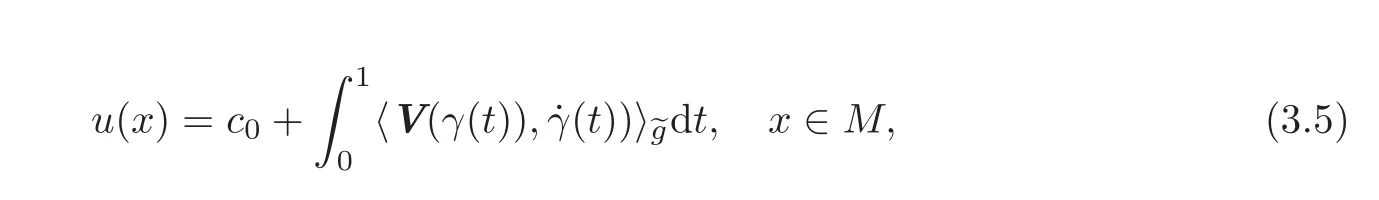
By(3.3)we clearly have for every j=1,···,n that

which is equivalent to∇Hu=a,see(3.1),i.e.,u∈C2(M)is a solution to(1.6).

It remains to prove the sub-Riemannian Ces`aro-Volterra path integral formula(1.9).To do this,let us fix an arbitrary horizontal path γ :[0,1]→ M,joining x0with x ∈ M.If γ has the local representation γ =(γ1,···,γn+1),its horizontality means that

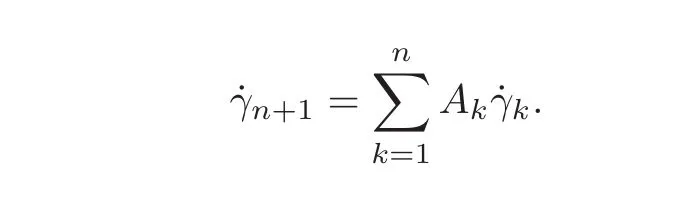
Considering every term at the moment t∈[0,1]in the following computations,we have

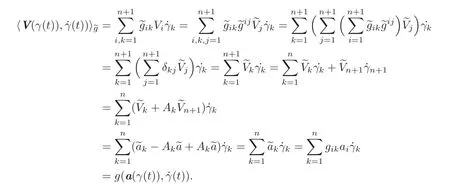
Thus,by(3.5)and the latter computation we obtain(1.9),which concludes our proof.

4 Examples

In this section we provide some computational examples as applications to Theorems 1.1 and 2.1 and Proposition 2.1,respectively.

4.1 Hyperbolic space

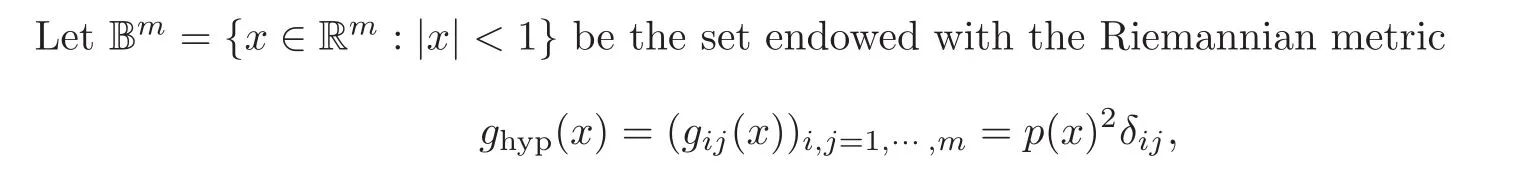
where

The pair(Bm,ghyp)is a model of the m-dimensional hyperbolic space with constant sectional curvature−1.

Example 4.1We solve the problem

where∇ghypdenotes the hyperbolic gradient.

A direct computation shows that ∂xi(pxj)= ∂xj(pxi)for every i,j=1,···,m,thus we may apply Theorem 2.1 on(Bm,ghyp),which implies the solvability of(4.1).Moreover,if γ :[0,1]→ Bmis γ(t)=tx with an arbitrarily fixed x ∈ Bm,the solution u can be obtained as

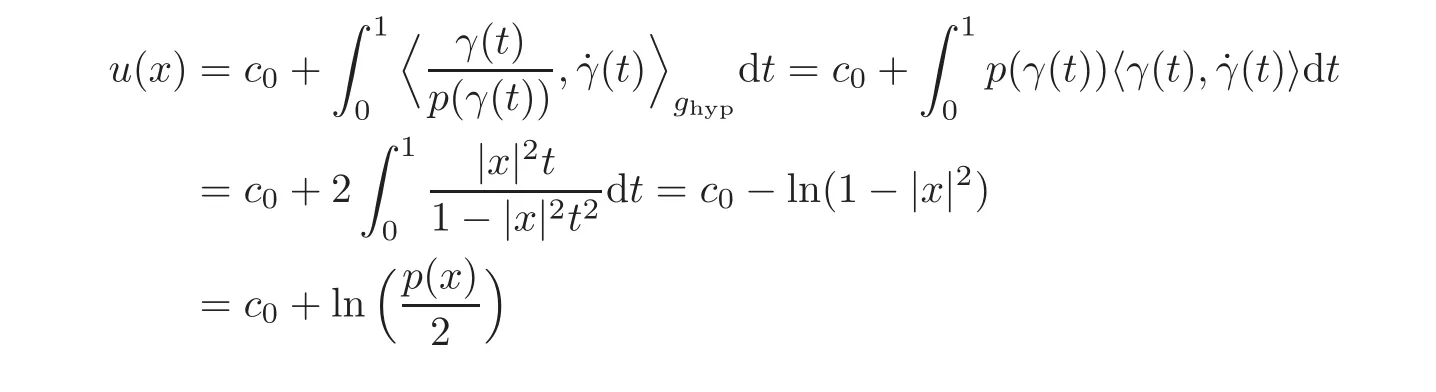
for any c0∈R.

For simplicity,in the next example we consider only the hyperbolic plane(B2,ghyp).

Example 4.2We solve the problem

4.2 Carnot and Heisenberg groups

Let G be an(n+1)-dimensional corank 1 Carnot group with the Lie algebra g=g1⊕g2,where dimg1=n and dimg2=1.Usually,the operation on g(in exponential coordinates on Rn×R)is given by

where x=(x1,···,xn+1),y=(y1,···,yn+1),and without loss of generality,A is represented by

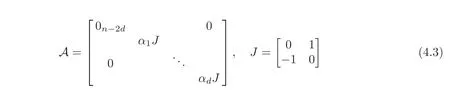
(see,e.g.[19]).Here 0＜ α1≤ ···≤ αd,and 0n−2dis the(n−2d)×(n−2d)square null-matrix.The layers g1and g2are generated by the left-invariant vectorfields

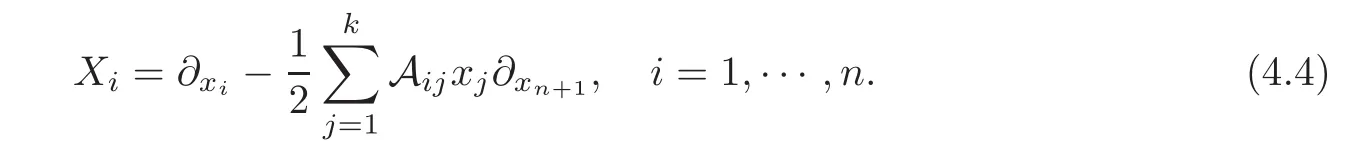
Note that[Xi,Xj]=Aij∂xn+1,i,j=1,···,n.

If n=2d(thus the kernel of A is trivial)and α1= ···= αd=4,the Carnot group G reduces to the usual Heisenberg group Hd=R2d×R.

For our example,we shall consider a 6-dimensional corank 1 Carnot group with the leftinvariant vectorfields given by(4.4),by choosing d=2,n=5,α1=4 and α2=2.To be more explicit,the distribution D on(G,◦)is formed by the vector fields given by

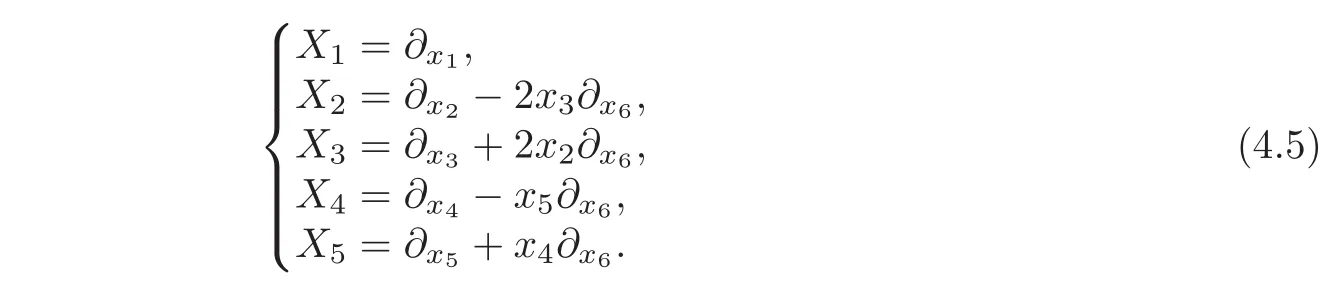
Let a=(a1,a2,a3,a4,a5)∈ Γ(D)be given by the functions

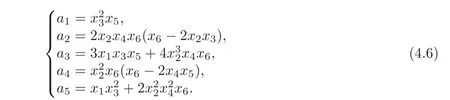
Example 4.3We solve the problem

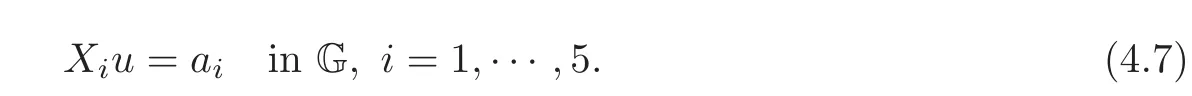
To do this,we are going to fully explore Theorem 1.1;by using the same notations,we identify A1=0,A2= −2x3,A3=2x2,A4= −x5,A5=x4.Moreover,c23=4= −c32,c45=2= −c54,and the rest of the elements of the matrix C=(cij)are zero,i,j=1,···,5.In order to solve(4.7),we have to check relations(1.7)and(1.8),respectively.It is easy to observe that(1.7)is relevant only for(i,j)=(2,3)and(k,l)=(4,5)(the other choices giving always zero),where simple computations give thatthus,(1.7)holds.Another simple reasoning shows that relation(1.8)is also verified;for instance,same way.

Thus,Theorem 1.1 implies that the system(4.7)is solvable in F(G);let x0=0∈G and any horizontal curve γ =(γ1,γ2,γ3,γ4,γ5,γ6):[0,1] → G with γ(0)=0 and γ(1)=x=(x1,x2,x3,x4,x5,x6)∈ G.Note that the horizontality of γ means that

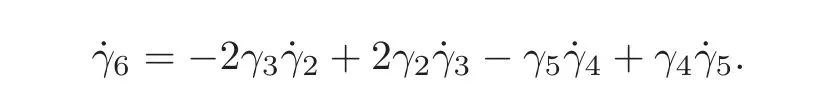
Due to the latter relation and(1.9),some suitable rearrangements and γ(0)=0 give that

for some c0∈R,which provides the solution of system(4.7).

5 Final Remarks

We conclude the paper with two remarks which can be considered as starting points of further investigations.

(I)Poincar´e lemma on Finsler manifoldsLet(M,F)be an m-dimensional,not necessarily reversible Finsler manifold and Ω⊆M be a simply connected domain.Given a vectorfield V ∈ C1(Ω,TΩ),we are asking about the solvability of the equation

where∇Fdenotes the Finslerian gradient.Here,as usual∇Fu(x)=J∗(x,Du(x)),where J∗:T∗M→TM is the Legendre transform associating to each element α ∈M the unique maximizer on TxM of the map y → α(y)−F2(x,y)and Du(x)∈M is the derivative of u at x ∈ M(see[18]).Note that in general,u → ∇Fu is not linear.In order to solve(5.1),a necessarily curl-vanishing condition can be formulated by using the inverse Legendre transform J=(J∗)−1and fundamental form of the Finsler metric F.However,we cannot adapt the proof of Theorem 2.1 into the Finsler setting.Indeed,we recall that in the proof of Theorem 2.1 we explored the metric compatibility and torsion-freeness of the Levi-Civita connection with respect to the given Riemannian metric;as we know,such properties are not simultaneously valid on a generic Finsler manifold unless it is Riemannian.

(II)Saint-Venant lemma on sub-Riemannian structuresFor simplicity,we shall consider only the usual Heisenberg group(Hd,D,g),where D={X1,···,X2d}with

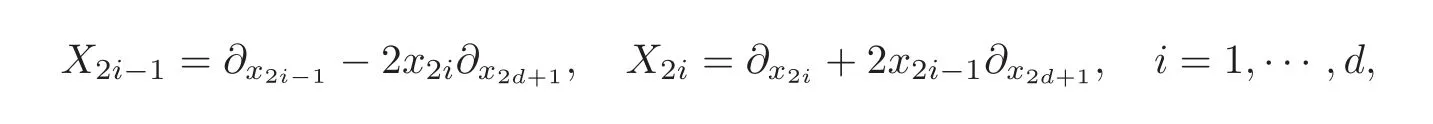
and g is the natural Riemannian metric on D(see(4.4)).Given a symmetric vectorfield e=(e1,···,e2d)∈ Γ(D)2don Ω ⊆ Hd,i.e.,eij=ejifor every i,j=1,···,2d where ei=the question concerns the solvability of the sub-Riemannian system

for the unknown vector field V=(V1,···,V2d) ∈ C∞(Ω,R2d),where the components of the symmertric horizontal gradient∇s,Hare given by

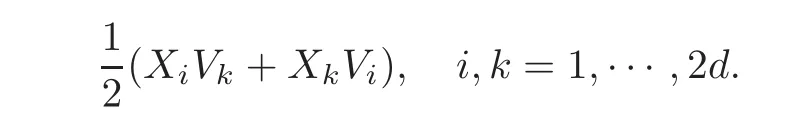
Thefirst challenging problem is to establish the necessary Saint-Venant compatibility relations associated to problem(5.2)and then to apply Proposition 2.1;note that Schwartz type properties are not valid in this setting since usually XiXj/=XjXifor i/=j.Moreover,weaker versions of the Saint-Venant lemma on Hdwould provide a sub-Riemannian Korn-type inequality as well.Clearly,more general sub-Riemannian structures can also be considered instead of Heisenberg groups verifying the assumptions of Theorem 1.1.

6 Appendix:Proof of the Saint-Venant Lemma(Proposition 2.1)

A direct computation shows that if(2.9)has a solution,then the Saint-Venant compatibility relations(2.10)trivially hold.

Conversely,the Saint-Venant compatibility relations(2.10)can be written into the form

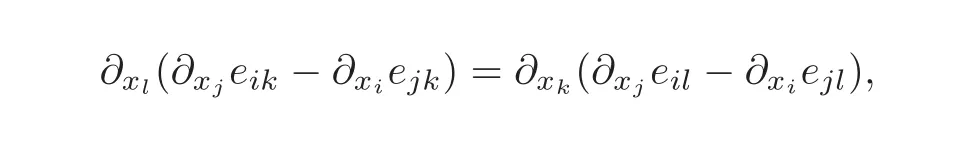
which is equivalent to

If Wijis a vector field on Ω with the representation

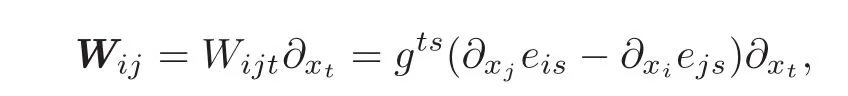
relation(6.1)can be written equivalently into the form

Thus,we may apply Theorem 2.1,i.e.,there exists pij∈ C2(Ω)such that

By components,the latter relation means that

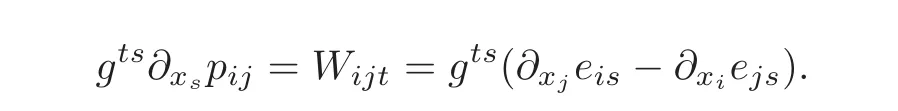
Multiplying from left by gtland adding them,we have

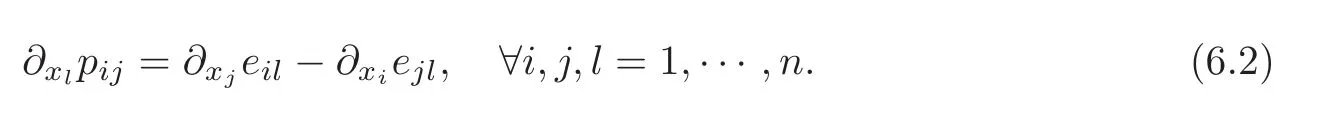
Since∂xlpij+∂xlpji=0,we can assume without loss of generality that pij+pji=0.

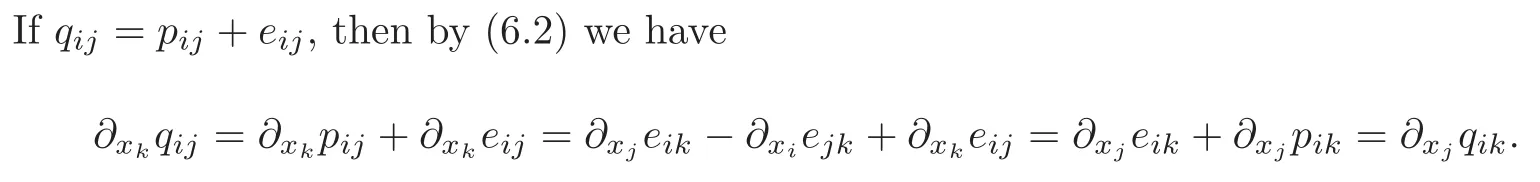
Again,the latter relation can be transformed into

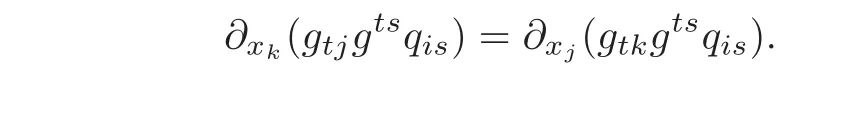
Therefore,if

Theorem 2.1 implies the existence of ui∈ C2(Ω)such that

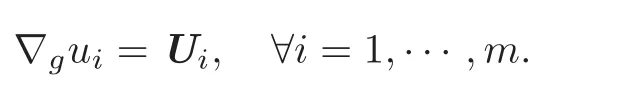
If we write the components of the latter relation,it yields that

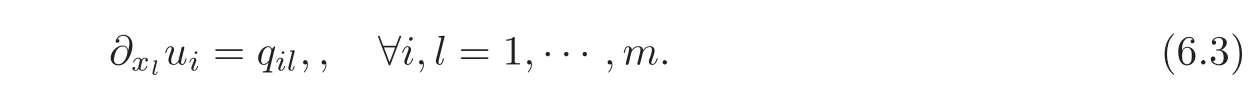
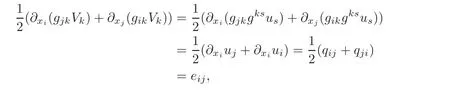
which is nothing but∇s,gV=e,i.e.,relation(2.9).The Ces`aro-Volterra integral formula follows at once by combining the above steps.

AcknowledgementsThe author thanks Professor Philippe G.Ciarlet for his invitation to the City University of Hong Kong where the present work has been initiated.He is also grateful to Professors Ovidiu Calin and Der-Chen Chang for their suggestions and remarks.

[1]Abraham,R.,Marsden,J.E.and Ratiu,T.,Manifolds,Tensor Analysis,and Applications,2nd edition,Applied Mathematical Sciences,75,Springer-Verlag,New York,1988.

[2]Agrachev,A.,Barilari,D.and Boscain,U.,Introduction to Geodesics in Sub-Riemannian Geometry,Geometry Analysis and Dynamics on Sub-Kiemannian Manifolds,II,EMS Ser.Lect.Math.,Eur.Math.Soc.,Zürich,2016.

[3]Amrouche,Ch.,Ciarlet,P.G.and Mardare,C.,Remarks on a lemma by Jacques-Louis Lions,C.R.Math.Acad.Sci.Paris,352(9),2014,691–695.

[4]Amrouche,Ch.,Ciarlet,P.G.and Mardare,C.,On a lemma of Jacques-Louis Lions and its relation to other fundamental results,J.Math.Pures Appl.(9),104(2),2015,207–226.

[5]Calin,O.and Chang,D.-C.,Sub-Riemannian Geometry,General Theory and Examples,Encyclopedia Math.Appl.,126,Cambridge University Press,Cambridge,2009.

[6]Calin,O.,Chang,D.-C.and Eastwood,M.,Integrability conditions for the Grushin and Martinet distributions,Bull.Inst.Math.Acad.Sin.(N.S.),8(2),2013,159–168.

[7]Calin,O.,Chang,D.-C.and Eastwood,M.,Integrability conditions for Heisenberg and Grushin-type distributions,Anal.Math.Phys.,4(1–2),2014,99–114.

[8]Calin,O.,Chang,D.-C.and Hu,J.,Poincar´e’s lemma on the Heisenberg group,Adv.in Appl.Math.,60,2014,90–102.

[9]Calin,O.,Chang,D.-C.and Hu,J.,Integrability conditions on Engel-type manifolds,Anal.Math.Phys.,5(3),2015,217–231.

[10]Calin,O.,Chang,D.-C.and Hu,J.,Integrability conditions on a sub-Riemannian structure on S3,Anal.Math.Phys.,7(1),2017,9–18.

[11]Chen,W.and Jost,J.,A Riemannian version of Korn’s inequality,Calc.Var.Partial Differential Equations,14,2012,517–530.

[12]Ciarlet,P.G.,Linear and nonlinear functional analysis with applications,Society for Industrial and Applied Mathematics,Philadelphia,PA,2013.

[13]Ciarlet,P.G.,Gratie,L.,Mardare,C.and Shen,M.,Saint Venant compatibility equations on a surface application to intrinsic shell theory,Math.Models Methods Appl.Sci.,18(2),2008,165–194.

[14]Ciarlet,P.G.and Mardare,S.,Nonlinear Saint-Venant compatibility conditions and the intrinsic approach for nonlinearly elastic plates,Math.Models Methods Appl.Sci.,23(12),2013,2293–2321.

[15]Ciarlet,P.G.,Mardare,S.and Shen,M.,Saint Venant compatibility equations in curvilinear coordinates,Anal.Appl.(Singap.),5(3),2007,231–251.

[16]do Carmo,M.P.,Riemannian Geometry,Birkhäuser,Boston,1992.

[17]Figalli,A.and Rifford,L.,Mass transportation on sub-Riemannian manifolds,Geom.Funct.Anal.,20(1),2010,124–159.

[18]Ohta,S.and Sturm,K.-T.,Heatflow on Finsler manifolds,Comm.Pure Appl.Math.,62(10),2009,1386–1433.

[19]Rizzi,L.,Measure contraction properties of Carnot groups,Calc.Var.Partial Differential Equations,55(3),2016,20 pages.