On Problems in the Calculus of Variations in Increasingly Elongated Domains

Hervé LE DRET Amira MOKRANE

(Dedicated to Philippe G.Ciarlet on the occasion of his 80th birthday)

1 Introduction

In this article,we revisit the“ℓ→+∞”problem in the context of the calculus of variations.This class of problems was introduced by Chipot and Rougirel[8]in 2000,see also[9]and the monographs by Chipot[4,6],and has since then given rise to many works by several authors dealing with various elliptic and parabolic problems up to until recently.

A prototypical ℓ→ +∞ problem is the following.Let ω =]−1,1[,ℓ＞ 0 be a real number and Ωℓ⊂ R2the rectangle]−ℓ,ℓ[×ω.We denote by x1the first variable in]−ℓ,ℓ[and x2the second variable in ω.Any function f ∈ L2(ω)in the second variable gives rise to a function in two variables still denoted f by setting f(x1,x2)=f(x2).We thus consider the two boundary value problems:Find uℓ,a function in(x1,x2),such that

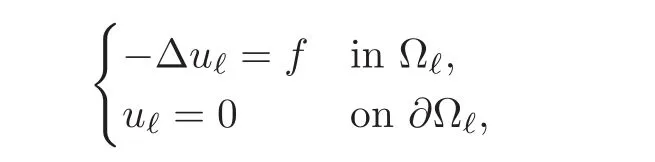
and find u∞,a function in x2,such that

Now the function u∞can also be considered as a function in two variables that is independent of x1.In this case,it can be shown that,for any ℓ0＞ 0,one has

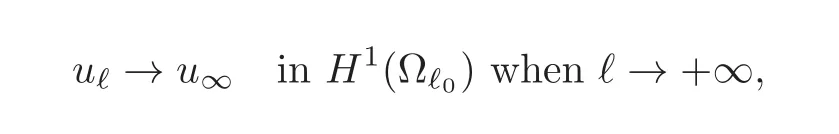
hence the name of the problem.In other words,when the data does not depend on the elongated dimension,the solution of the above boundary value problem converges in some sense atfinite distance to the solution of the correspondingboundary value problem posed in the non-elongated dimension when the elongation tends to infinity.

The majority of works on the ℓ→ +∞ problem makes use of the boundary value problem itself,i.e.,the PDE plus boundary condition.Exceptions to this rule are the recent papers[5,7],in which the authors considered instead a sequence of problems in the calculus of variations posed on elongated domains(see also[6]).This is the approach we adopt here as well.

Our main motivation for this is that certain models,such as nonlinear hyperelasticity,are naturally posed as problems in the calculus of variations for which no Euler-Lagrange equation,i.e.,non underlying PDE even in a weak form,is available(see[2]).Moreover,questions surrounding the Saint Venant principle in elasticity(see[16—17]),are typically set in elongated domains,albeit in one direction only.Consequently,it makes sense to attempt dealing with some ℓ→ +∞ problems by using only energy minimization properties and no Euler-Lagrange equation whatsoever.

We are however quite far from achieving the goal of treating nonlinear elasticity,since the approach that we develop below relies a lot on convexity,whereas convexity is not an appropriate hypothesis for nonlinear elasticity.We are nonetheless able to encompass a wide range of nonlinear energies,including the p-Laplacian with some technical restrictions on the number of elongated dimensions with respect to the exponent p.Our hypotheses are weaker and our results are sometimes stronger than those of[7].The techniques are somewhat different too,with an emphasis here on weak convergence and weak lower semicontinuity techniques,and reliance on such classical techniques as the De Giorgi slicing method which are not dependent on convexity.As a general rule,we try to make as little use of convexity as we can at any given point.

Let us describe our results a little more precisely.We consider bounded open subsets Ωℓof Rnwhich are Cartesian products of the form ℓω′× ω′′,with ω′⊂ Rrand ω′′⊂ Rn−r,with 1 ≤ r ≤ n − 1.We let x=(x′,x′′)with x′∈ Rrbeing the elongated variable and x′′∈ Rn−rthe non-elongated variable.Likewise,for a scalar-valued function v:Ωℓ→ R,we decompose the gradient ∇v=(∇′v,∇′′v)with obvious notation.

We consider an energy density F:Rn→ R and a function f on ω′′,and introduce the minimization problem offinding

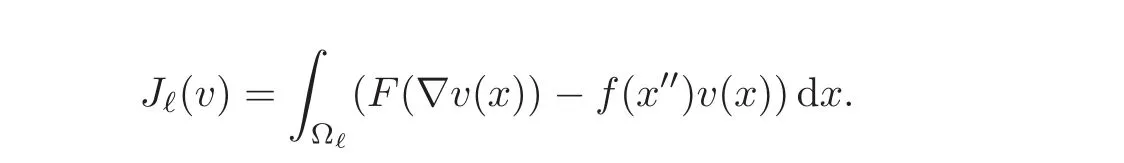
We assume that F has p-growth,p-coerciveness and is convex.In particular,there is no assumption of strict convexity or uniform strict convexity made on F.

We then introduce F′′:Rn−r→ R by letting F′′(ξ′′)=F(0,ξ′′),again with obvious notation.Of course,F′′is convex,has p-growth and p-coerciveness and the minimization problem offinding

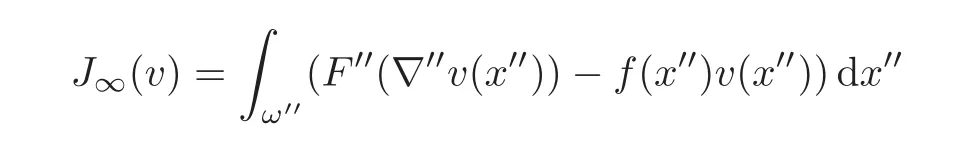
admits solutions.It turns out that,under additional hypotheses,this problem is the“ℓ→ +∞”limit of the family of minimization problems under consideration.

These hypotheses include appropriate growth and coerciveness hypotheses on the function G:Rn→ R,G(ξ)=F(ξ)− F′′(ξ′′),of the form

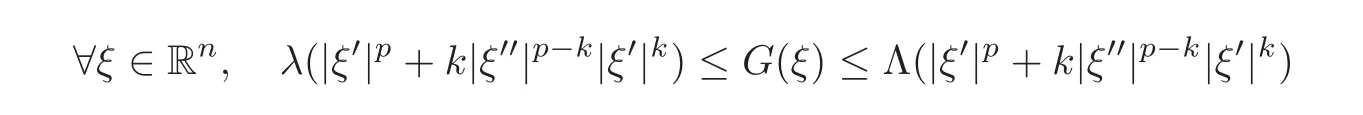
for some 0＜λ≤Λ and 0≤k＜p.Depending on the case,there is no more additional hypothesis(for k=0),or a hypothesis of strict convexity of F′′,or a hypothesis of uniform strict convexity of F′′(for k ＞ 0).

The results are a“ℓ→+∞”convergence in the weak sense for k=0 when r＜p,sharpened to strong sense when F′′is furthermore assumed to be strictly convex,and a strong“ℓ→ +∞”convergence for k＞0 when r≤.In the case of the p-Laplacian,p ＞ 2,we thus obtain strong“ℓ→+∞”convergence when r＜,see also[18].

In addition,in the case k=0,if we assume that F′′is uniformly strictly convex,we obtain strong convergence at an exponential rate without any restriction on r.This includes the known behavior of the 2-Laplacian in the“ℓ→ +∞”context.

We conclude the article with a few comments and perspectives on the vectorial case,in connection with nonlinear elasticity in particular.

2 Statement of the Problem

We consider two bounded open sets ω′⊂ Rrwith 0 ∈ ω′and ω′is starshaped with respect to 0,and ω′′⊂ Rn−rwith n ＞ r ≥ 1.Let ℓ＞ 0 and set

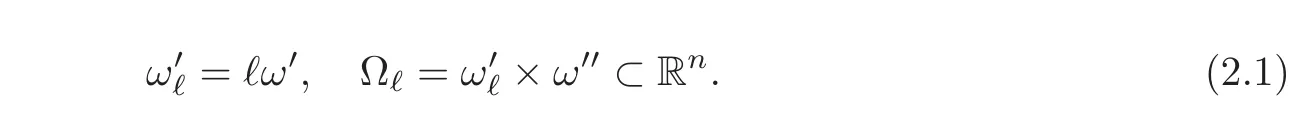
Points x in Ωℓwill be denoted by x=(x′,x′′)with x′=(x1,x2,···,xr)∈and x′′=(xr+1,···,xn) ∈ ω′′.Likewise,vectors ξ in Rnwill be decomposed as ξ=(ξ′,ξ′′),with ξ′∈ Rrand ξ′′∈ Rn−r.

Note that because of the starshaped assumption,we have Ωℓ⊂ Ωℓ′as soon as ℓ≤ ℓ′and we are thus dealing with a “growing”family of open sets.We make an additional regularity hypothesis on ω′,which is as follows.Define first the gauge function of ω′as

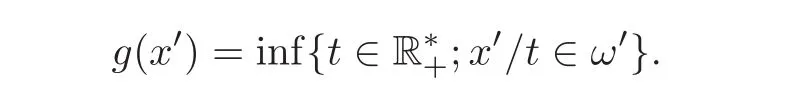
Since ω′is starshaped and bounded,this is well defined,={x′;g(x′)＜ ℓ},and there exists 0 ＜ R1＜ R2such that R1|x′|≤ g(x′)≤ R2|x′|for all x′∈ Rr.

Now we assume that ω′is such that g is a Lipschitz function with Lipschitz constant K.By Rademacher’s theorem,this implies that g is almost everywhere differentiable,with|∇′g(x′)|≤K a.e.Moreover,it is known that g then belongs to(Rr)and that its almost everywhere derivatives equal its distributional derivatives.This is true for example if ω′is convex.This regularity hypothesis is for convenience only:We use g to build cut-offfunctions inside the domains,and not up to the boundary.It should be quite clear that our results can be rewritten in order to accommodate arbitrary open sets ω′.

We are interested in a sequence of problems in the calculus of variations Pℓof the form

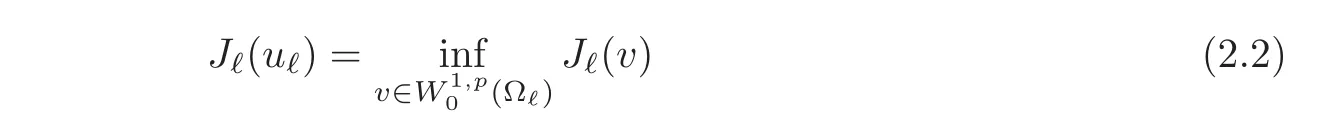
with uℓ∈and

where f′′∈ Lp′(ω′′),+=1,is a given function.Observe that the term corresponding to the force term for this problem only depends on the “non-elongated” variable x′′so that it is reasonable to expect that uℓbehaves as a function mostly in x′′in the limit ℓ→ +∞,in a sense made precise below.We could also consider more general semilinear force terms of the form h(x′′,v)satisfying appropriate growth and convexity assumptions,but we stick here with a linear term for simplicity.

We assume that the energy density F:Rn→R is convex.We let

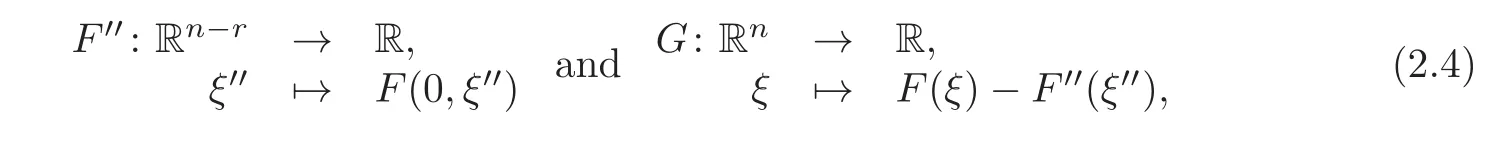
so that

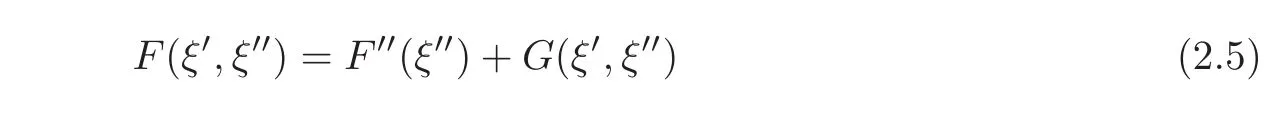
and F′′is convex.These functions are assumed to satisfy the following coerciveness and growth hypotheses

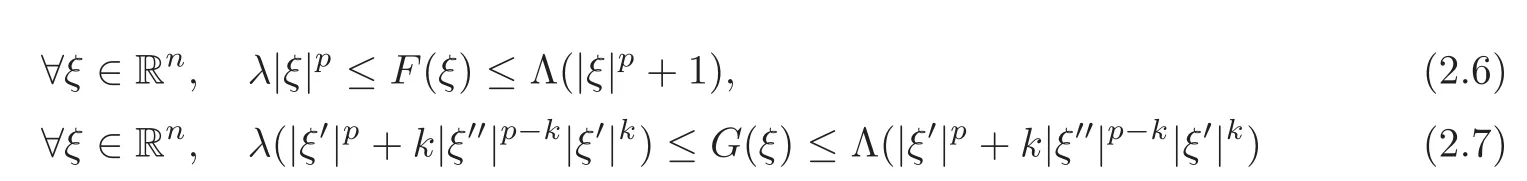
for some 0＜ λ ≤ Λ,p＞ 1 and 0≤ k ＜ p.1Note that k=p yields the same hypothesis as k=0.Here,for ξ∈ Rd,|ξ|denotes the canonical Euclidean norm of ξ in Rd.

Clearly,condition(2.6)implies the similar condition for F′′.

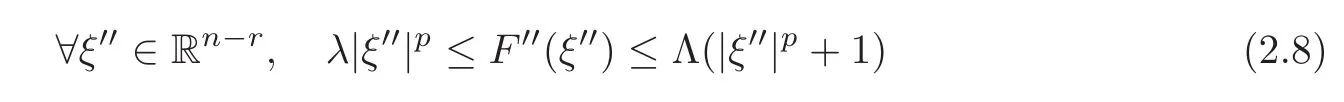
Energy densities of the form above include that associated with the p-Laplacian for p≥2.Indeed,in this case,F(ξ)=and we can take k=2 for p ＞ 2,or k=0 for p=2.Another simple energy density that is covered by our analysis is F(ξ)=or more generally energies of the form F(ξ)=F′(ξ′)+F′′(ξ′′),with appropriate hypotheses on F′and F′′.Here,assuming without loss of generality that F′(0)=0,we have G(ξ′,ξ′′)=F′(ξ′)and we can take k=0.

In addition to the above growth and coerciveness hypotheses,which obviously imply that problem Pℓhas at least one solution uℓ,we assume that F′′is uniformly strictly convex for k ＞ 0,in the sense that there exists a constant β ＞ 0 such that for all ξ′′,ζ′′∈ Rn−rand all θ,µ ∈ [0,1]with θ+ µ =1,we have

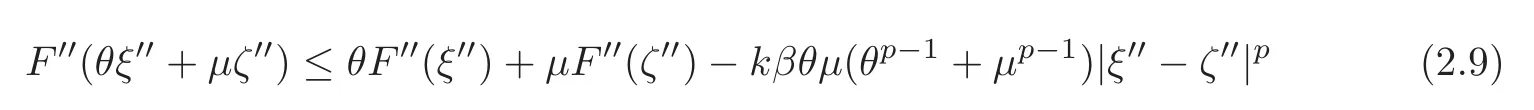
(see for instance[1,12,14]).The p-Laplacian for p ＞ 2,k=2,satisfies this hypothesis(the 2-Laplacian satisfies the alternate hypothesis(5.1)that will be used later on in Section 5).Note that when k=0,the hypothesis becomes redundant,and there is actually no requirement of even strict convexity,let alone uniform strict convexity,of F′′in this case.

We now introduce our candidate limit problem P∞as that offinding u∞∈(ω′′)such that

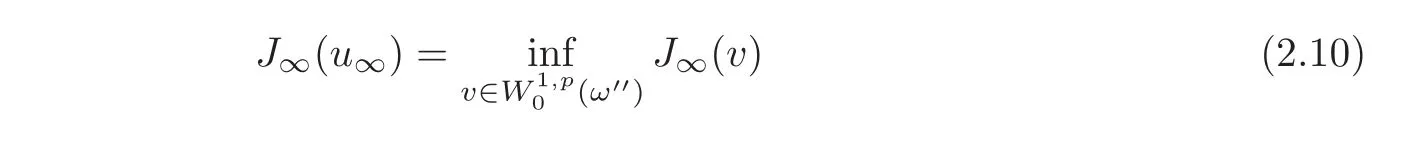
with

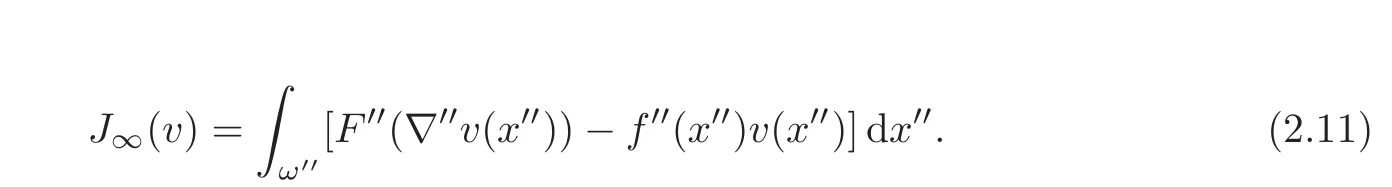
It is also clear that problem P∞has at least one solution u∞.

Here and in the sequel,we use the following notational device

that we apply indifferently to functions defined either on Ωℓor on ω′′.For brevity,we refer to∇′as the “horizontal” part of the gradient and to ∇′′as the “vertical” part of the gradient.

We want to study the asymptotic behavior of uℓwhen ℓ→ +∞ and compare it with a minimizer u∞of the n−r dimensional vertical problem P∞.Actually,our goal is to show that the former converges to the latter in a sense that will be explained later on.

3 Preliminary Estimates

Wefirst give several estimates that we will use in the proofs of our convergence results.Thefirst estimate follows immediately from Poincaré’s inequality.

Lemma 3.1There exists a constantc1=c1(ω′′)independent ofℓsuch that for allv ∈W1,p(Ωℓ)whose trace vanish on× ∂ω′′,we have

Let us now give a first,coarse estimate of uℓ.

Lemma 3.2There exists a constantc2independent ofℓ,such thatZ

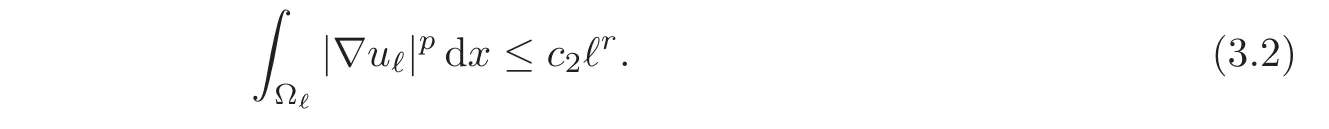
ProofLet us take v=0 as a test-function in problem(2.2).It follows that

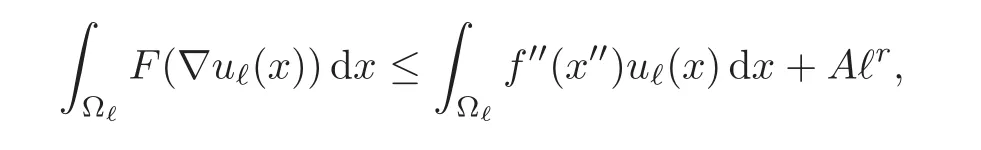
where A=F(0)Lr(ω′)Ln−r(ω′′)does not depend on ℓ(Lddenotes the d-dimensional Lebesgue measure).By Hö lder’s inequality and the coerciveness assumption(2.6),it follows that

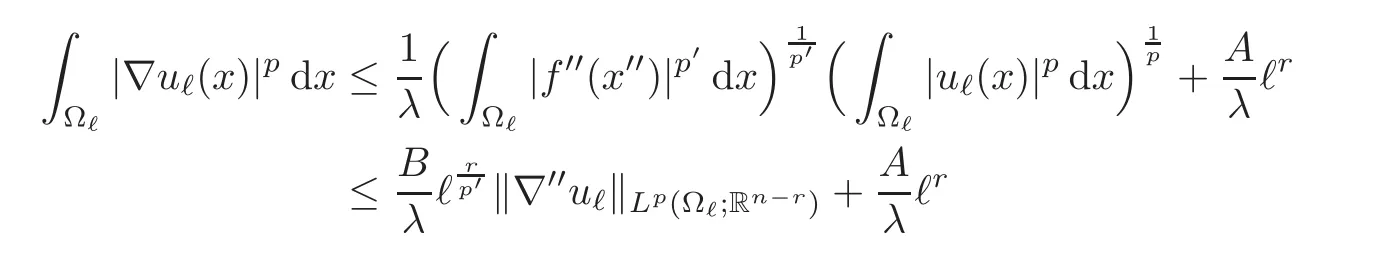
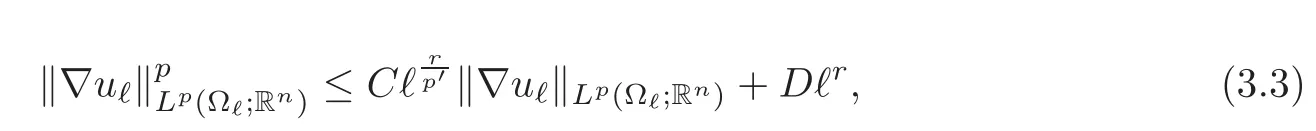
where C and D are constants that do not depend on ℓ.Let us set X=.Estimate(3.3)now reads

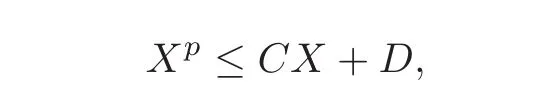
so that there exists c2depending only on C and D such that X≤which completes the proof.

We now recall an elementary estimate similar to what can be found in[13]for instance.

Lemma 3.3Leth(t)be a nonnegative bounded function defined on an interval[τ0,τ1],τ0≥ 0.Suppose that forτ0≤ t＜ s ≤ τ1,we have

whereC,D,ν1,ν2,θare nonnegative constants with0 ≤ θ＜ 1.Then,for allτ0≤ t＜ s ≤ τ1,we have

wherecis a constant that only depends onν1,ν2andθ.

ProofIf we have two sequences of nonnegative numbers aiand bisuch that ai≤ θai+1+bi+1,it follows by induction thatWe apply this remark to the sequences ai=h(ti)and bi+1=C(ti+1−ti)−ν1+D(ti+1−ti)−ν2,where ti=t+(1−σi)(s−t),0 ＜ σ ＜ 1 to be chosen later on,is an increasing sequence in[τ0,τ1]such that t0=t.This yields the estimate

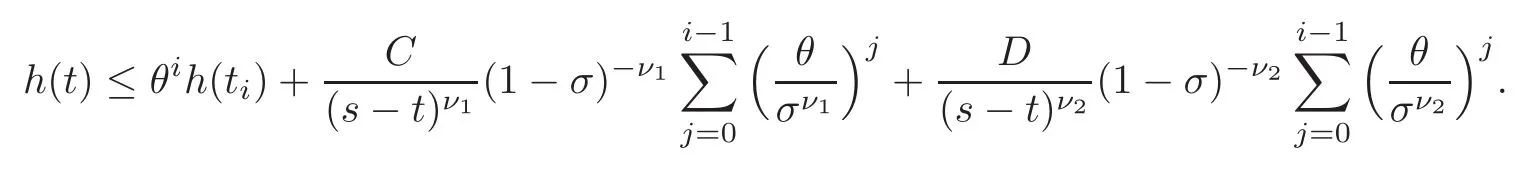
We now choose σ ＜ 1 in such a way that＜1,and conclude by letting i→+∞,remembering that h(ti)is bounded.

Next,we estimate the horizontal part of the gradient of uℓin Lp(Ωℓ0)in terms of ℓ,ℓ0,uℓand a minimizer u∞of the vertical problem P∞.

Theorem 3.1There exists a constantc3independent of all the other quantities,such that for all0＜t＜ s≤ ℓand all minimizersu∞of the vertical problem,we have

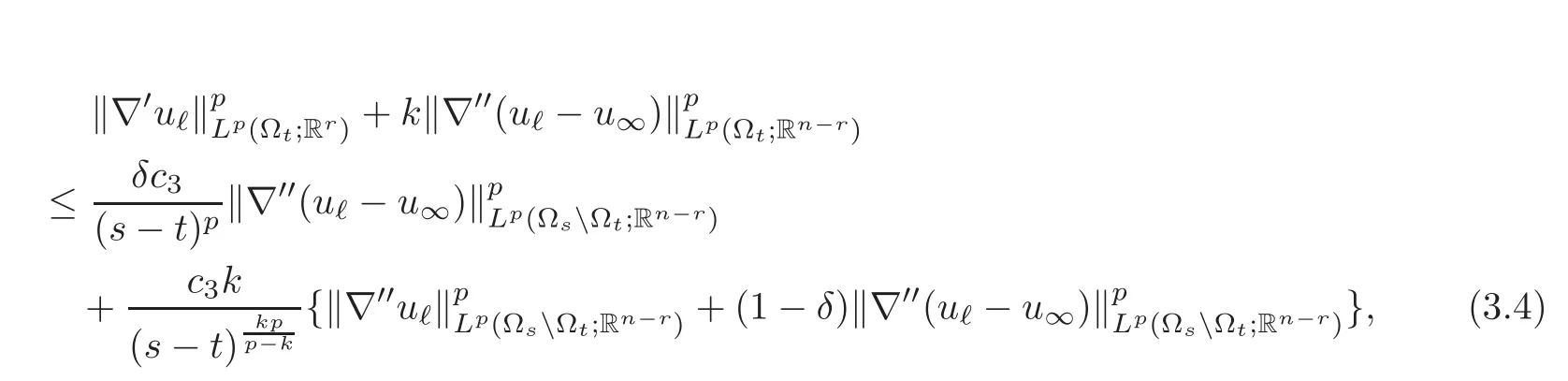
whereδ=1if0≤ k≤,δ=0otherwise.

ProofWe first define a family of cut-off functions as follows.For all 0＜ t＜ s≤ ℓ,we set

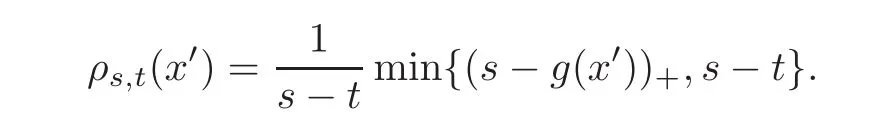
By the definition of the gauge function,we see that ρs,t≡0 onand 0 ≤ ρs,t≤ 1.By our regularity assumption on ω′,ρs,tis Lipschitz and such that

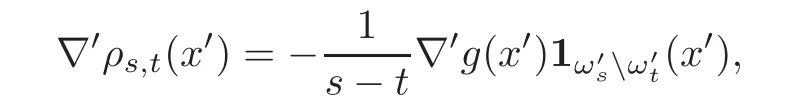
so that we can estimate

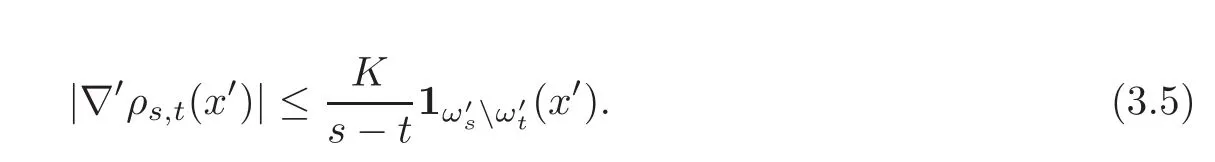
We pick a number 0＜α＜1 and then set

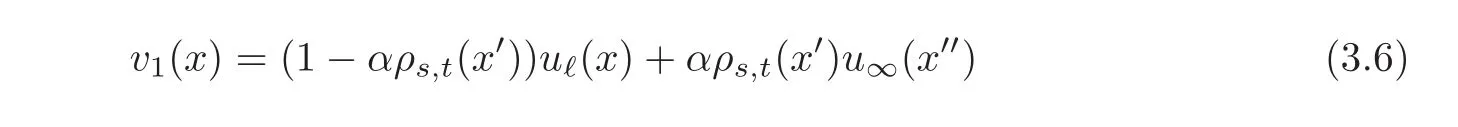
and

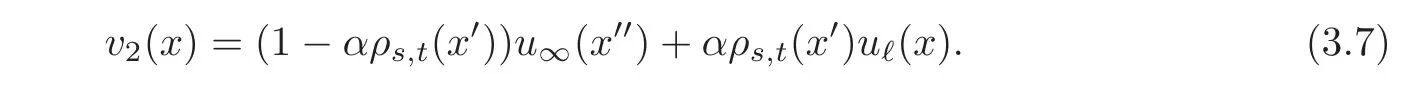
Clearly,v1belongs toand is thus a suitable test-function for problem Pℓ,hence

Integrating estimate(3.9)over,we obtain

We add estimates(3.8)and(3.10)together and note that all the terms involving f′′cancel out since v1+v2=uℓ+u∞.Therefore

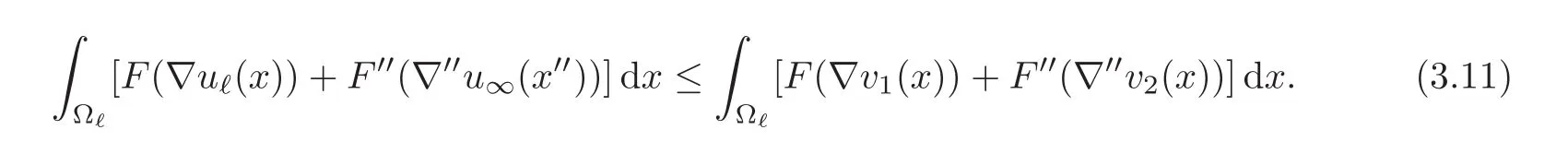
We observe that v1=uℓand v2=u∞on ΩℓΩs,so that estimate(3.11)boils down to

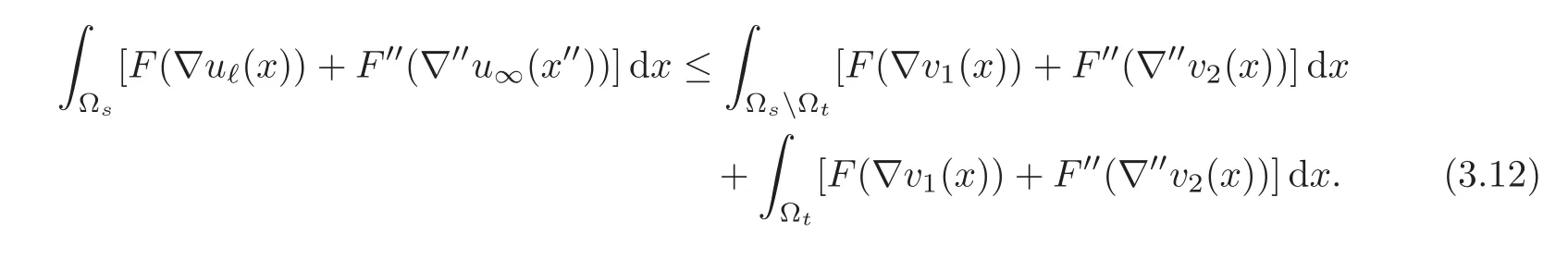
The left-hand side of(3.12)can be rewritten as

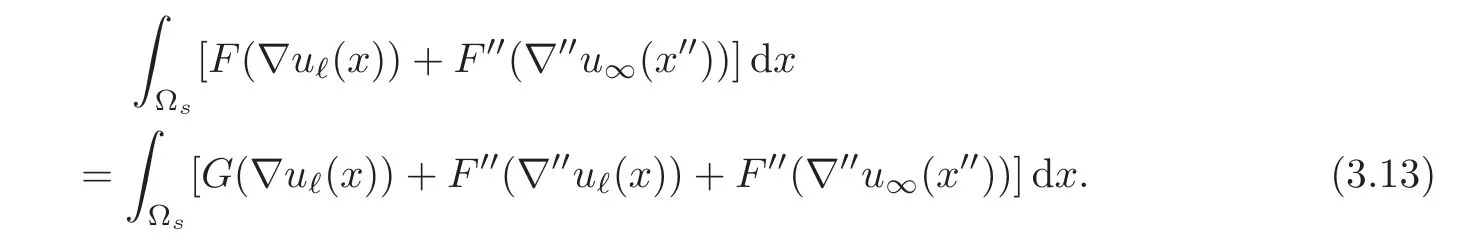
Let I1and I2be thefirst and second integrals in the right-hand side of(3.12).To estimate I1,we just use the convexity of F′′,since the vertical gradients of v1and v2are convex combinations of the vertical gradients of uℓand u∞,

To estimate I2,we note that v1=(1−α)uℓ+αu∞and v2= αuℓ+(1−α)u∞on Ωt,thus owing to the convexity of F and the uniform convexity(2.9)of F′′,

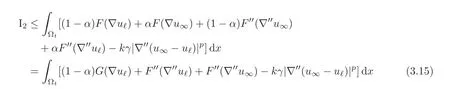
for some γ ＞ 0.Putting estimates(3.12),(3.14),(3.15)and equation(3.13)together,we obtain

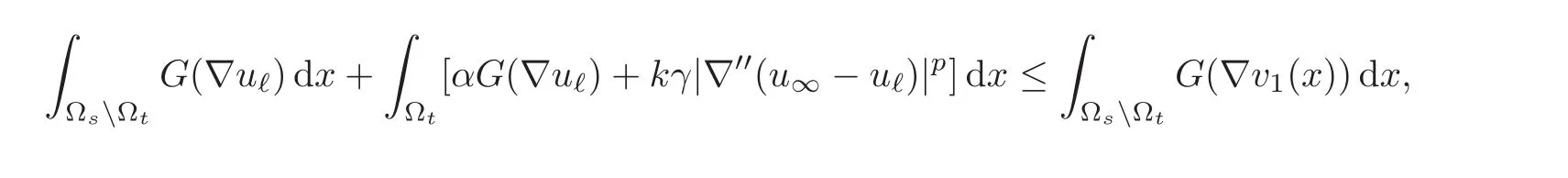
which,upon using the coerciveness hypothesis(2.7),yields

where a＞0 is a small generic constant that only depends on the other constants involved.

We now focus on estimating the right-hand side of(3.16).We have

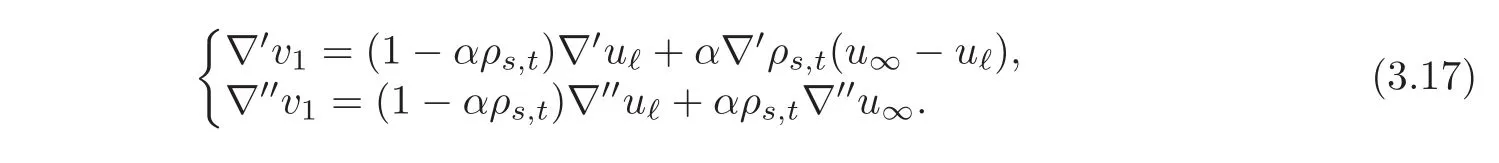
Based on(3.17)and the definition of ρs,t,we have the following estimates for any exponent q:

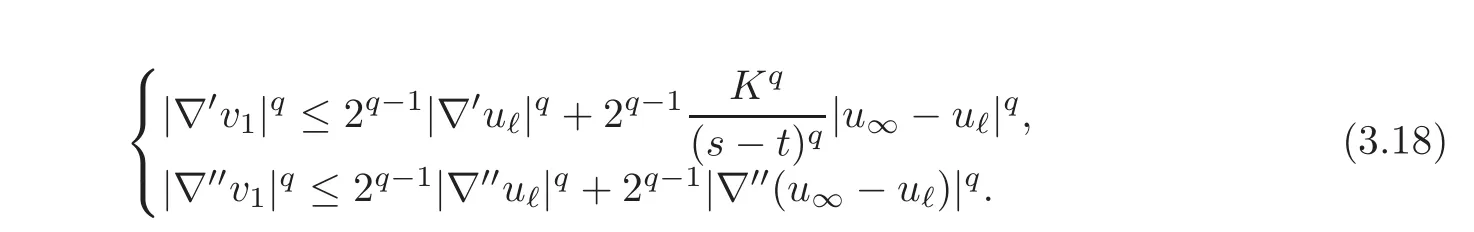
We will use exponents q=p and q=k for thefirst line and q=p−k for the second line.Due to the growth hypothesis(2.7),we have

where A is a large generic constant that only depends on the other constants involved.For k≥1,three of the four product terms that appear need to be estimated.For this purpose,we will use Young’s inequality in the following form

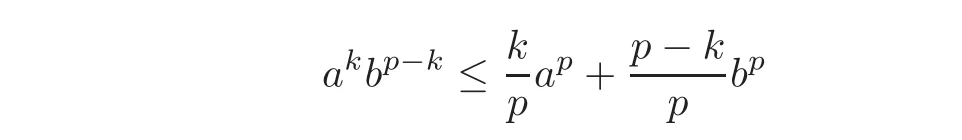
for a,b≥0(recall that p＞k).We thus obtain

where A is another generic constant.We integrate this inequality over ΩsΩtand use Poincaré’s inequality in the vertical variables to obtain

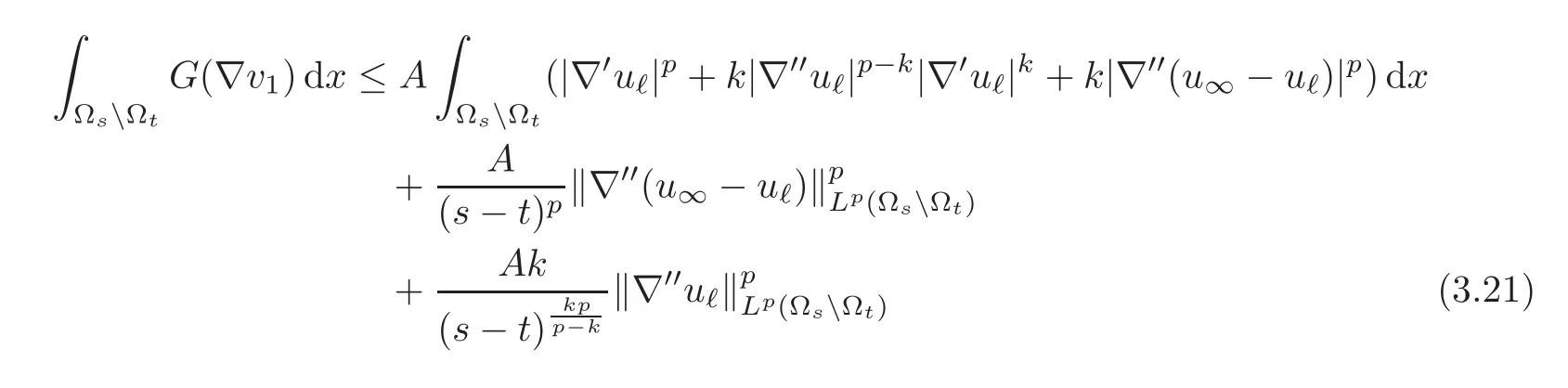
with A yet another generic constant.

We now consider two different cases.First,for 0≤ k ≤,let us set

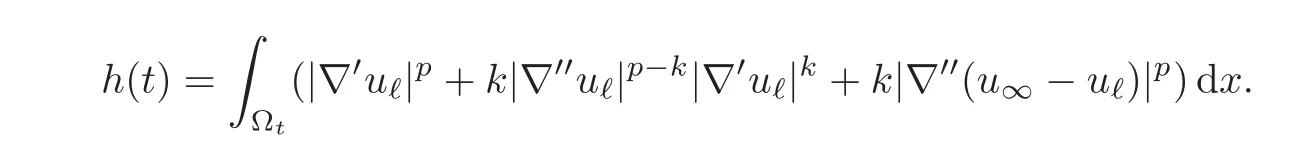
Inequalities(3.16)and(3.21)may be rewritten as

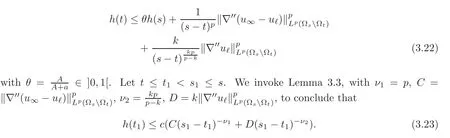
The result follows in this case by letting t1→t and s1→s since the constant c only depends on ν1,ν2and θ,and h is continuous(recall that δ=1).

with the same function h,but with another value for θ,which we do not write here.We conclude as before with Lemma 3.3 and thefirst constant C=0 for instance.

The following is an immediate consequence of the previous estimate.

Corollary 3.1We have,for allℓ≥ ℓ0,

whereδ=1if0≤ k≤δ=0otherwise.

ProofIndeed,we take s= ℓ,t= ℓ0and notice that Ωℓ Ωℓ0⊂ Ωℓ.

Let us remark that if k=0 and there is actually no strict convexity assumption made on F′′,i.e.,F′′may well be not strictly convex,the previous result boils down to

However,when k＞0,we make crucial use of the uniform strict convexity to derive the estimate.

Let us close this section with an estimate similar to that obtained in Lemma 3.2.Recall that uℓis a minimizer on Ωℓ,whereas the following estimate is on Ωℓ0.See[5]for a very similar argument.

Lemma 3.4There exist constantsandc4,independent ofℓ,such that for all≤ ℓ0≤ ℓ,

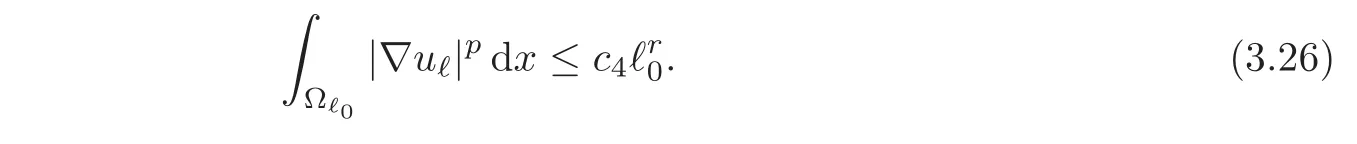
ProofLet 1 ≤ t≤ ℓ− 1 and set ρt= ρt+1,t.We take vt,ℓ=(1− ρt)uℓas a test-function in problem(2.2).This test-function is equal to uℓ“far away” and is 0 in Ωt.We obtain

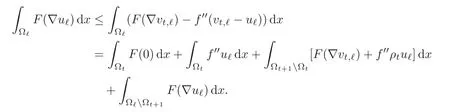
Therefore we see that

Furthermore

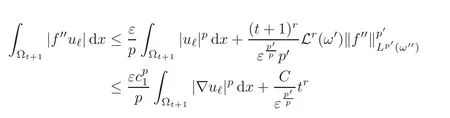
with ε ＞ 0 to be chosen afterwards.

Let us set

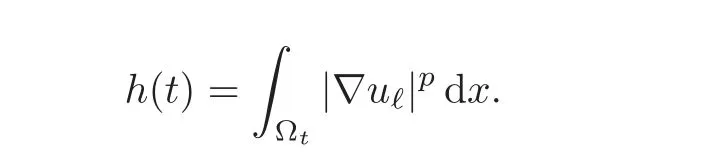
Putting all the above estimates together,it follows that

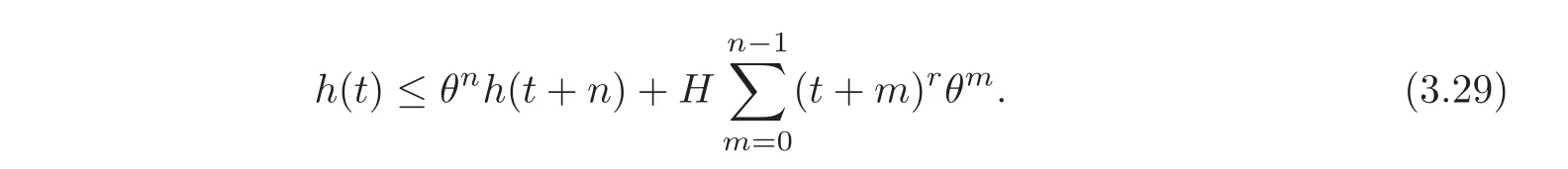
Let us now set t= ℓ0.We have h(ℓ0+ ℓ− ℓ0」)≤ h(ℓ)≤by Lemma 3.2.Hence

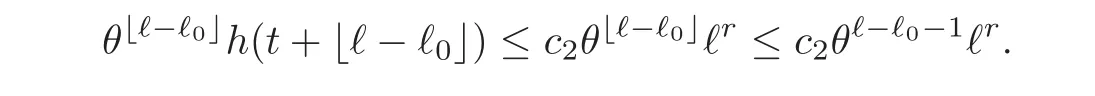
Now,for ℓ0≥the function in the right-hand side is decreasing,hence maximum forℓ= ℓ0.Therefore

for ℓ≥ ℓ0≥ −Moreover,for ℓ0≥ 1,

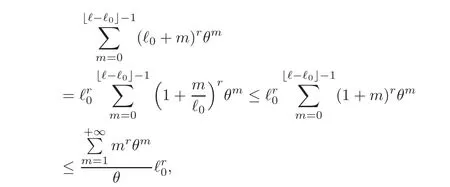
which completes the proof with

We now turn to the convergence results.As a consequence of Lemma 3.4,we have the theorem,without any restriction on r with respect to p and k,as follows.

Theorem 3.2There exists a subsequenceℓ→ +∞and a functionu∗∈suchthat,for allℓ0,

Moreover,u∗=0on∂Ω∞.

Note that the weak convergence above implies that uℓ⇀ u∗weakly inWe will sometimes omit the restriction notation in the sequel when unnecessary.

ProofBy estimates(3.1)and(3.26),for all n ∈ N∗,uℓis bounded in W1,p(Ωn).Using the diagonal procedure,we thus construct a sequence ℓnsuch that for all m,in W1,p(Ωm),with um=0 on× ∂ω′′.Now,since Ωm⊂ Ωm′as soon as m≤m′,it followsso that we have constructed a single limit function u∗in the desired class.Furthermore,for all ℓ0,if we choose an integer m ≥ ℓ0,we see that convergence(3.30)holds true.

In the sequel,we will always consider a weakly convergent subsequence uℓin the sense of Theorem 3.2.

4 Identification of the Limit When ℓ→ +∞

In this section,we do not make any further use of assumption(2.9)of uniform strict convexity of F′′,other than the fact that we used it to establish Theorem 3.1.2Keep in mind that this hypothesis is void for k=0 anyway.The results will only hold for values of r small enough depending on p.We let Ω∞=Rr× ω′′.

Let usfirst show that the asymptotic behavior of uℓis independent of the elongated dimension if r is small enough.

Theorem 4.1Assume thatr＜pifk=0,or thatr＜if0＜ k＜ p.Then we have∇′u∗=0andu∗may be identified with a function in thex′′variable only,still denotedu∗,which belongs to(ω′′).

ProofBy estimates(3.2)and(3.25)and the triangle inequality,it follows that

when ℓ→ + ∞ w ith ℓ0fixed.Indeed,when 0 ＜ k ≤,we actually have≤ p and sinceℓ→ + ∞,thefirst term in the right-hand side of estimate(4.1)is bounded from above by the second term.

In order to get a feeling of what Theorem 4.1 says,let us look at a few examples.For the Laplacian,we have p=2 and we can take k=0,which restricts this result to r=1(see Section 5 for a more general result with additional hypotheses,that applies in this case).For the p-Laplacian,p＞2,we can take k=2 and the result is restricted to r＜.This restriction for the p-Laplacian can already be found in[18].Note that r=1 and r=2 are allowed for any value of p.This is not optimal in this particular case,since it is known thatℓ→+∞ convergence holds without restriction on the dimension with respect to p(see[10]).

Let us now identify the limit function.Wefirst need another estimate.

Lemma 4.1There exists a constantc5such that for allt≤s,

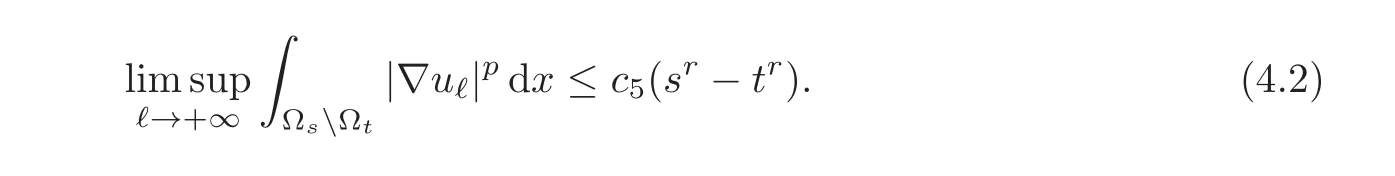
ProofWe may assume that t＞0,since the case t=0 is already covered by Lemma 3.4.We use here De Giorgi’s classical slicing trick.Let n be an integer large enough so that 0≤t−1n＜s+1n≤ℓ.For each integer m,1≤m≤n,we consider the cut-offfunction

and that Sm,n∩ Sm′,n= Ø when m/=m′.

Let us consider the test-function vℓ,m,n=(1−χm,n)uℓ+χm,nu∗.The minimization problem yields the estimate

Taking into account the specific form of the cut-off function,this implies that

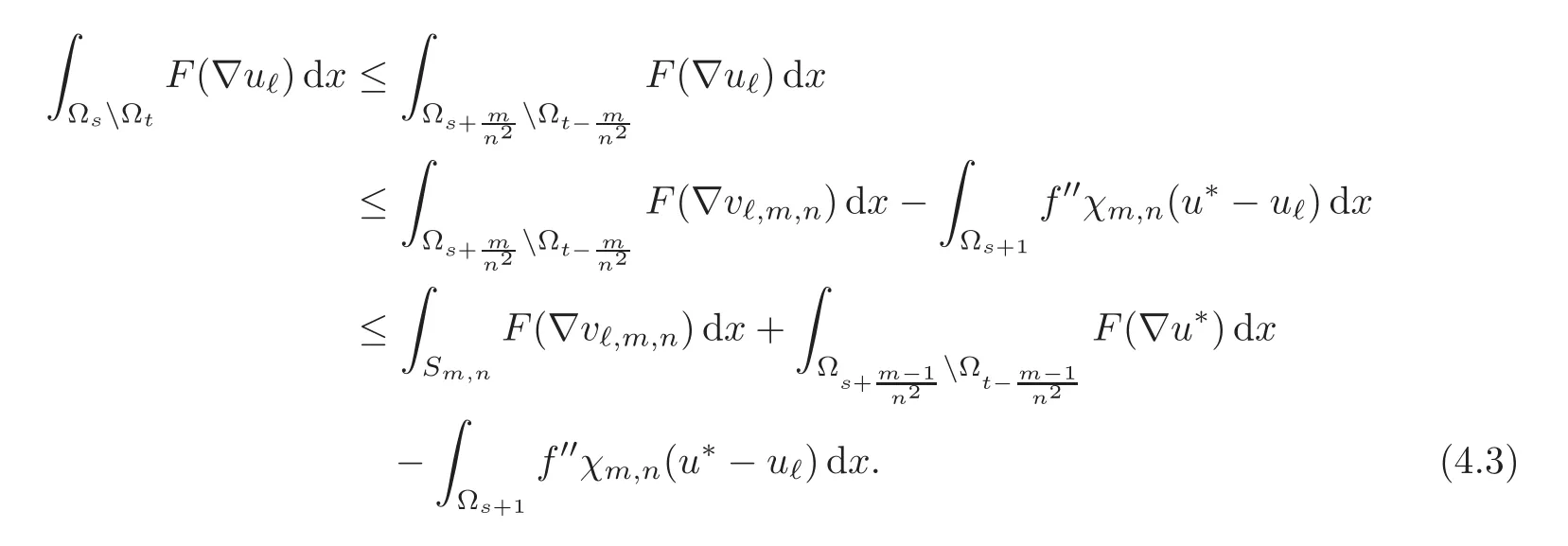
Let us estimate each term in the right-hand side separately.First of all,we have

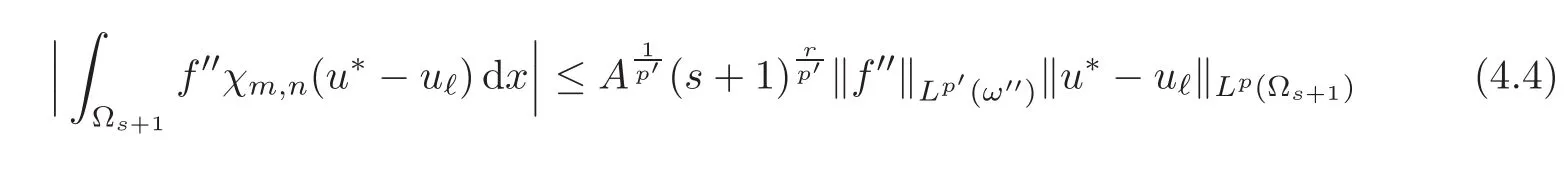
with A=Lr(ω′).Secondly,we see that

We now come to the slicing argument stricto sensu.By the growth estimate(2.6),we have

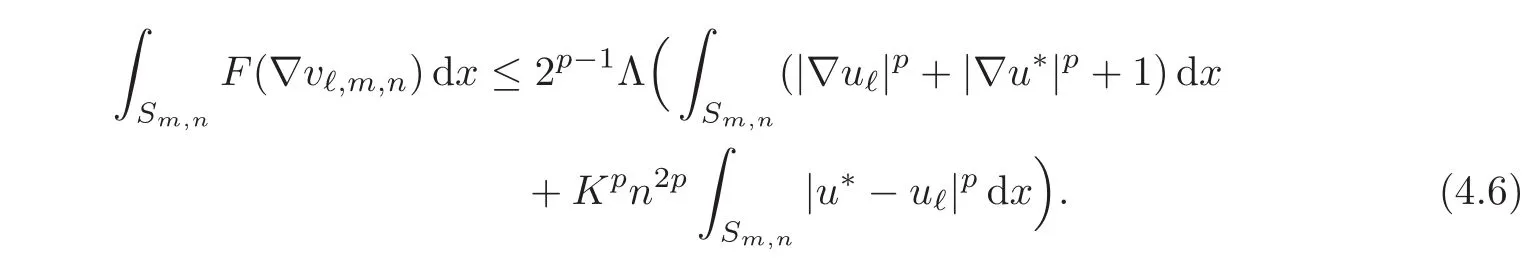
The only term that causes a difficulty is the last term coming from ∇χm,n.We now plug estimates(4.4)—(4.6)into the right-hand side of estimate(4.3),sum for m=1 to n and divide the result by n.Observing that the sum of integrals over the slices Sm,ngives rise to integrals over the union of all slices,which is included in Ωs+1,this yields

We first let ℓ→ +∞.Due to the Rellich-Kondraˇsov theorem,follows from the coerciveness estimate that

We finally let n → +∞ to obtain the result with

We now are in a position to prove the main result of this section.

Theorem 4.2The functionu∗is a minimizer of problemP∞.

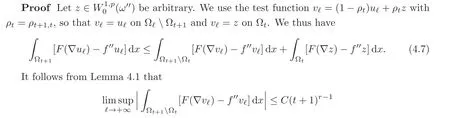
for some constant C independent of ℓ and t.The left-hand side of estimate(4.7)is weakly lower-semicontinuous,hence,letting ℓ→ +∞,we obtain

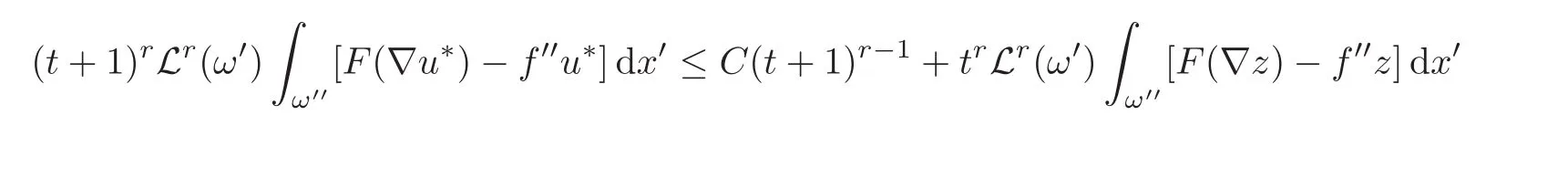
and the result follows from letting t→ +∞,since F(∇u∗)=F′′(∇′′u∗)and F(∇z)=F′′(∇′′z).

We now use a classical trick to obtain strong convergence when F′′is strictly convex.Of course,when k＞0,this is already the case by assumption(2.9).Strict convexity is only a new assumption if k=0.In this case,the solution u∞of the limit problem is unique and this uniqueness implies the weak convergence of the whole family uℓ.

Theorem 4.3Assume thatF′′is strictly convex.Thenu∗=u∞anduℓ→ u∞strongly inW1,p(Ωℓ0)for allℓ0.

We recall the following two lemmas that can be found e.g.in[3].

Lemma 4.2LetF:RM→Rbe strictly convex.Letµ∈]0,1[andaj,a∈RMsuch that

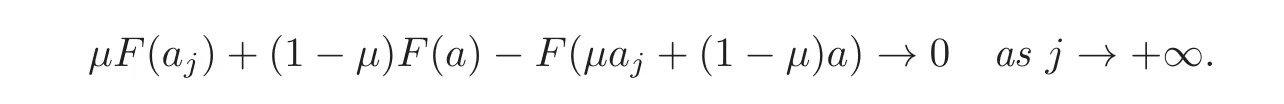
Thenaj→a.

The second lemma is a slight variation on Fatou’s Lemma.

Lemma 4.3LetFj,F,Hj,H∈L1(Ω)withFj≥Hj≥0for allj,Fj→FandHj→Ha.e.,andRΩFjdx→RΩF dx.Then

Proof of Theorem 4.3We already know that∇′uℓ→ 0= ∇′u∗strongly in Lp(Ωt)by estimate(4.1).We thus just have to prove the strong convergence of∇′′uℓ.

We use a similarslicing as before,with the test-functions1≤m≤n.Skipping the details,this slicing implies that

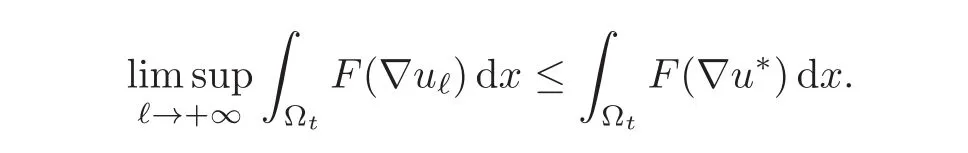
On the other hand,for almost all x′,the function ux′,ℓ:x′′→ uℓ(x′,x′′)is an admissible test-function for the limit problem,so that

We integrate this inequality with respect to x′∈ tω′and obtain

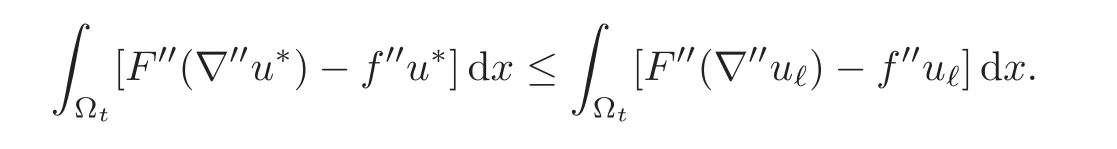
We now let ℓ→ +∞,which yields

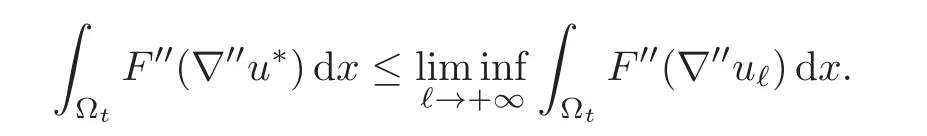
By hypothesis(2.7),G ≥ 0,which implies that F′′(ξ′′) ≤ F(ξ′,ξ′′)for any ξ′.It follows that

when ℓ→ +∞,since F′′(∇′′u∗)=F(∇u∗).

Let us pickµ∈]0,1[and set

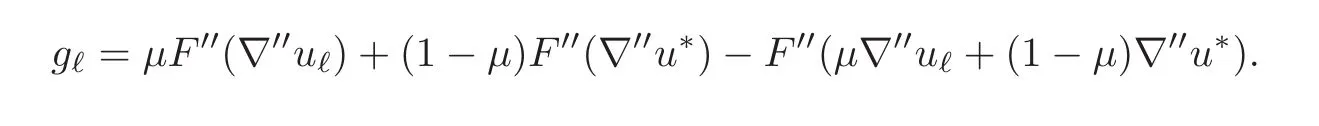
By weak lower semicontinuity,it is clear that

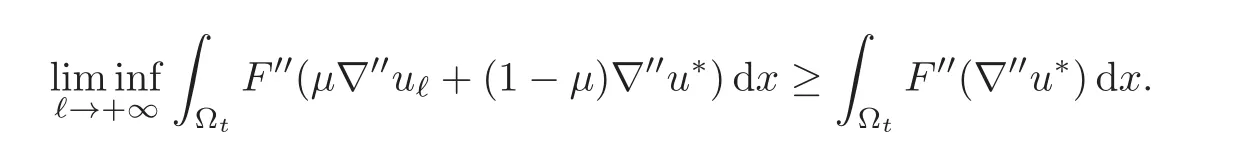
Therefore

so that gℓ→ 0 a.e.(up to a subsequence).We then use Lemma 4.2 to deduce that∇′′uℓ→ ∇′′u∗a.e.up to that same subsequence.

We now let

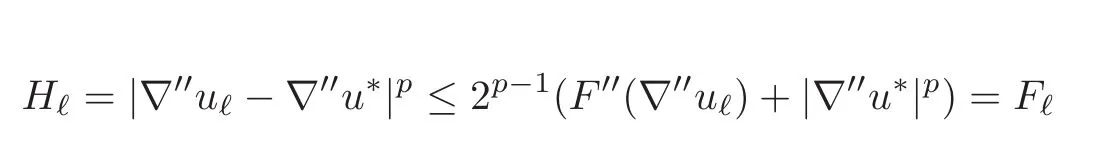
and invoke Lemma 4.3 and(4.8)to obtain the result for ℓ0=t.To conclude for all ℓ0,we use the diagonal process.

5 Convergence Rates

In the previous section,we obtained convergence results without taking advantage of the term involving k in the left-hand side of estimate(3.25).This makes them valid in particular for k=0 without strict or uniform strict convexity.It should however be clear that for k＞0,the term in question can be used to obtain a much shorter convergence proof with convergence rate,which we do not detail here.More precisely,we have the result below.

Theorem 5.1Under the previous hypotheses with0＜k＜pandr＜,we have

The proof is a direct consequence of Corollary 3.1 and Lemma 3.2.

In any case,the estimates do not seem to allow a convergence proof without any restriction on r with respect to p in all generality,whereas it is known in some cases,for instance in the case of the Laplacian,that convergence holds true for all values of r.

In order to partially overcome these shortcomings,we assume now that k=0 and that F′′is uniformly strictly convex in the sense that

for some β＞0.Note that this is equivalent to allowing k=p in hypotheses(2.7)and(2.9).In some sense,is then infinite and it is to be expected that there should be no restriction on the allowed dimensions r,plus faster than polynomial convergence.This is what we now proceed to show.

Under assumption(5.1),it is fairly clear that we still have an estimate similar to that of Theorem 3.1,namely,

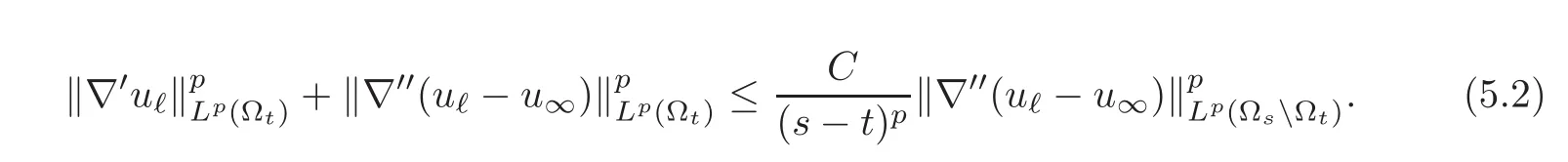
Let us thus prove that not only does convergence hold without restrictions on the elongated dimension r,but that it also occurs at an exponential rate.The extra control makes things actually much easier.

Theorem 5.2Under hypotheses(2.6)–(2.7)withk=0and(5.1),then for allr ≤ nand allℓ0,there exist constantsCandα ＞ 0independent ofℓsuch that we have

ProofWe take s=t+1 in estimate(5.2),which yields

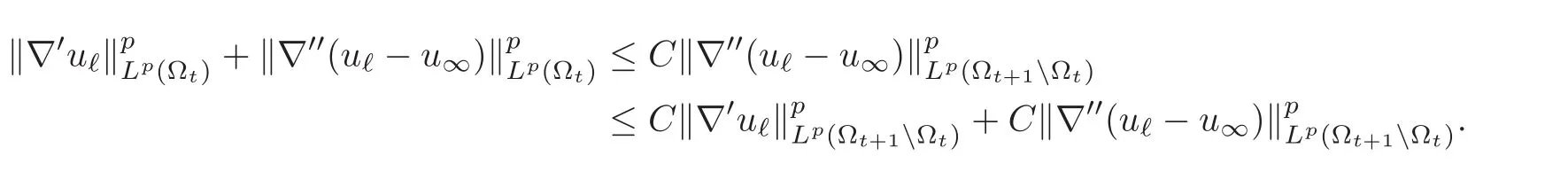
Setting

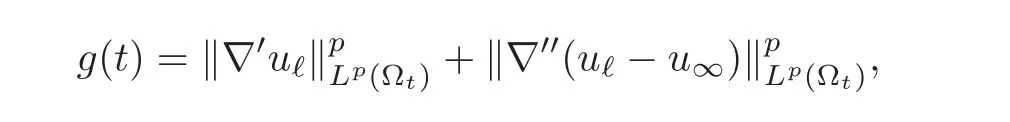
we have just shown that

or in other words

We iterate inequality(5.3)using the sequence tn=n+ ℓ0,n=0,···, ℓ− ℓ0」.Obviously

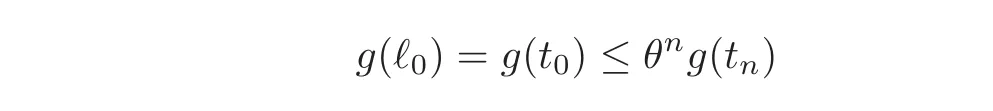
for all such n,and in particular for the last one,

with lnθ＜ 0.Now,for all r we can pick α such that lnθ＜ pα ＜ 0 and eℓlnθℓr≤ e−pαℓfor ℓlarge enough,which completes the proof since∇′u∞=0.

Theorem 5.2 applies to energies of the form F(ξ)=F′(ξ′)+F′′(ξ′′),for instance.We recover in particular the known result for the case of the 2-Laplacian.See also the monograph[6]for exponential estimates in this context.

6 Extension to the Vectorial Case

We have written everything so far in the context of a scalar problem,i.e.,the functions uℓare scalar-valued.All previous developments only made use of the minimization problem,under various convexity assumptions.Now clearly,absolutely nothing is changed if we consider instead vector-valued problems in the calculus of variations,with functions uℓtaking their values in some RN,if the energies are supposed to satisfy the same growth,coercivity and convexity assumptions as before,and the same convergence results hold true.

Unfortunately,in the vectorial case of the calculus of variations,the relevant condition that guarantees lower-semicontinuity of the energy functional is not convexity,but much weaker conditions such as quasiconvexity,or in the case of energies that can take the value+∞,as is the case in nonlinear elasticity,polyconvexity,see[11].Indeed,convexity is not suitable in nonlinear elasticity for well-known modeling reasons.This explains why we have striven to use as little convexity as possible(in some sense)at any given point in the sequence of arguments.This comment should however be mitigated by the fact that some instances of our uses of convexity will also work with rank-1-convexity,which is a reasonable assumption in the vectorial case.There are also notions of strict uniform quasiconvexity that may apply,see[12].

The fact that the Euler-Lagrange equation is not available in nonlinear elasticity is also an incentive to try and only use the minimization problem.Now,it is at this point unclear to us how to attack the elongation problem in such nonconvex vectorial cases,since we still heavily rely on(strict uniform)convexity at crucial points of the proofs.Moreover,the Dirichlet boundary condition considered here is not necessarily the most interesting one in the context of nonlinear elasticity,in particular if we have the Saint Venant principle in mind.

Even the potential limit problem is not so clear.In another dimension reduction context,when considering a body whose thickness goes to zero,and with different boundary conditions,it can be seen that quasiconvexity is not conserved through an “algebraic” formula of the kind found here,and that a relaxation step is necessary(see for instance[15]).Physically,this due to the possibility of crumpling such a thin body.A similar phenomenon may quite possibly happen here,but maybe not in the same fashion.

To the best of our knowledge,the nonconvex vectorial case remains open.

[1]Attouch,H.and Aze,D.,Approximation and regularization of arbitrary functions in Hilbert spaces by the Lasry-Lions method,Annales de l’Institut Henri Poincaré(C)Non Linear Analysis,10,1993,289–312.

[2]Ball,J.M.,Convexity conditions and existence theorems in nonlinear elasticity,Arch.Rational Mech.Anal.,63,1977,337–403.

[3]Ball,J.M.and Marsden,J.E.,Quasiconvexity at the boundary,positivity of the second variation and elastic stability,Arch.Rat.Mech.Anal.,86,1984,251–277.

[4]Chipot,M.,ℓ Goes to Plus Infinity,Birkhäuser,Basel,Boston,Berlin,2002.

[5]Chipot,M.,On the asymptotic behaviour of some problems of the calculus of variations,J.Elliptic Parabol.Equ.,1,2015,307–323,DOI:10.1007/BF03377383.

[6]Chipot,M.,Asymptotic Issues for Some Partial Differential Equations,Imperial College Press,London,2016.

[7]Chipot,M.,Mojsic,A.and Roy,P.,On some variational problems set on domains tending to infinity,Discrete Contin.Dyn.Syst.,36(7),2016,3603–3621.

[8]Chipot,M.and Rougirel,A.,Sur le comportement asymptotique de la solution de probl`emes elliptiques dans des domaines cylindriques tendant vers l’infini,C.R.Acad.Sci.Paris Sér.I Math.,331(6),2000,435–440.

[9]Chipot,M.and Rougirel,A.,On the asymptotic behaviour of the solution of parabolic problems in cylindrical domains of large size in some directions,Discrete Contin.Dyn.Syst.Ser.B,1(3),2001,319–338.

[10]Chipot,M.and Xie,Y.,Some issues on the p-Laplace equation in cylindrical domains,Tr.Mat.Inst.Steklova,261,2008,Differ.Uravn.i Din.Sist.,293–300;translation inProc.Steklov Inst.Math.,261(1),2008,287–294.

[11]Dacorogna,B.,Direct Methods in the Calculus of Variations,2nd ed.,Springer-Verlag,New York,2000.

[12]Evans,L.C.,Quasiconvexity and partial regularity in the calculus of variations,Arch.Rational Mech.Anal.,95,1986,227–252.

[13]Giaquinta,M.,Introduction to regularity theory for nonlinear elliptic systems,Lectures in Mathematics ETH Zürich,Birkhäuser,Basel,1993.

[14]Juditsky,A.and Nesterov,Y.,Deterministic and stochastic primal-dual subgradient algorithms for uniformly convex minimization,Stoch.Syst.,4(1),2014,44–80.

[15]Le Dret,H.and Raoult,A.,The nonlinear membrane model as variational limit of nonlinear threedimensional elasticity,J.Maths.Pures Appl.,74,1995,549–578.

[16]Mielke,A.,Normal hyperbolicity of center manifolds and Saint-Venant’s principle,Arch.Rational Mech.Anal.,110,1990,353–372,DOI:10.1007/BF00393272.

[17]Toupin,R.A.,Saint-Venant’s principle,Arch.Rational Mech.Anal.,18,1965,83–96.

[18]Xie,Y.,On Asymptotic Problems in Cylinders and Other Mathematical Issues,Ph.D.thesis,Univ.Zürich,2006.