电动汽车再生制动能量回收最优控制策略

郭金刚, 董昊轩, 盛伟辉, 涂 超

(长安大学 汽车学院, 陕西 西安 710064)

电动汽车在节能、环保、改善车辆性能等方面具有诸多优势,但其一次充电续驶里程普遍较短.再生制动技术能够在汽车制动时回收汽车动能,可以有效地提高电动汽车续驶里程[1].对于特定结构的电动汽车,影响再生制动能量回收的因素主要有电动汽车动力系统设计、运行阶段的控制策略和制动工况.在确定电动车整车结构、动力系统参数后,控制策略和制动工况成为提高再生制动能量回收效果的关键因素[2].

传统电动汽车再生制动控制策略主要是制动力分配策略,制定时并未考虑制动工况的影响.提高能量回收的方法多依据动力系统结构、电动机和电池工作特性、制动法规和相关约束条件等因素制定,通过控制分配前后轴制动力、电动机和摩擦制动力,实现能量回收和制动稳定性优化[3-4]，或是制定策略时采用模糊控制、滑模变结构控制等算法,改善再生制动控制效果[5-6].目前在制动工况对制动能量回收影响方面的研究,多集中在制动工况解耦后,对单一因素的分析[7-8],也未能将分析结果应用于再生制动控制策略的制定.若能从汽车制动状态控制的角度出发,考虑制动工况对制动能量回收的影响,并以此优化传统再生制动控制策略,则可以使能量回收效率得以提高.

制动工况分为单次工况和循环工况.循环工况多用于电动车性能测试,日常驾驶中驾驶员操作多属于单次工况,包括滑行和一次制动2种状态.文中以单次工况为研究工况,主要包含2个因素:制动强度和制动初始速度.笔者以集中电动机前轴驱动电动汽车为研究对象,综合分析单次工况对能量回收效果的影响,得到不同制动初始速度下能量回收最佳的最优制动强度,并以能量回收最大化为目标,提出一种再生制动能量回收最优控制策略.通过与理想再生制动控制策略对比,对最优控制策略的能量回收效果进行评价和验证.

1 再生制动能量回收影响因素分析

制动时电动汽车动能主要通过行驶阻力和制动系统消耗,制动系统中一部分能量由再生制动系统回收,另一部分由机械摩擦作用转换成热能消耗或在能量传递过程中损失[9],影响能量回收的因素可分为3类: ① 影响制动总能量的因素,主要是制动初始和终止速度、电动汽车质量等; ② 影响可回收能量的因素,如再生制动系统结构、驱动系统布置形式、电动汽车结构(滚动阻力消耗、空气阻力消耗等)、制动力分配策略(摩擦制动损耗)和制动强度等; ③ 影响再生制动回收能量的因素,如电动机和电池工作特性、传动系统特性、各部件及传递线路损耗和控制器损耗等.

制动总能量、可回收能量和再生制动回收能量三者之间的关系如图1所示.

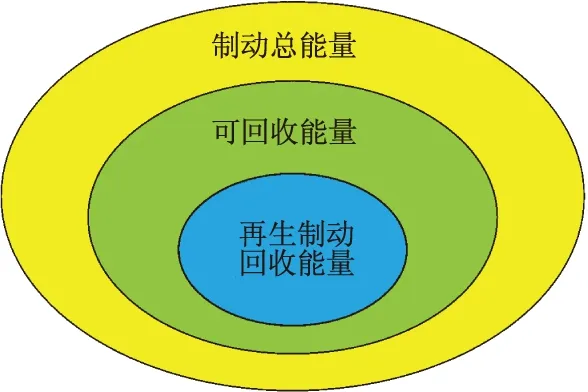
图1 各能量关系

单次工况中,影响制动总能量的因素一般已确定,则此时提高制动回收能量的方式主要有: ① 提高可回收能量,即采用合适的再生制动系统结构、减少行驶阻力消耗、以合适的强度制动、回收制动能量的驱动轴要多、分配到驱动轴上的制动力尽可能多等; ② 提高再生制动回收能量,即减少再生制动系统能量转化过程损耗,如减少电动机、电池、传动系统和控制器等产生的损耗,再生制动系统承担的功率应与电动机峰值功率相匹配,电池有能力回收电动机转化的能量等.

再生制动控制策略起到统筹作用,制定时要充分考虑以上影响因素.单次工况中,制动初始速度一般已确定,在其他影响因素确定的前提下,若能选择合适强度制动,则可以提高可回收能量,进而提高再生制动回收能量.

2 联合仿真模型

在联合仿真模型中,电动机、电池和控制策略等模型使用MATLAB/Simulink建立,电动汽车整车模型在CarSim下建立.整车模型基于CarSim中B级车模型,将原车驱动、制动系统去掉,驱动和制动转矩由MATLAB/Simulink模型提供.研究的车型为集中电动机前轴驱动,整车参数:整车质量为1 231 kg;轴距为2.60 m;质心到前轴距离为1.04 m;质心高度为0.54 m;车轮滚动半径为0.304 m;迎风面积为1.6 m2;空气阻力系数为0.343;滚动阻力系数为0.016.联合仿真模型以及各模块信号传递如图2所示.

图2 MATLAB/Simulink与CarSim联合仿真模型

为方便研究,建模时做如下假设: ① CarSim中车辆模型都是传统汽车,建立电动汽车整车模型时,忽略各模块修改带来的质量变化; ② 假定电动汽车行驶在平直路面上,忽略坡度和弯道带来的影响,仿真时取路面附着系数为0.8; ③ 本文不深入研究电动机和电池效率、传动系统效率带来的影响,建模时依据试验数据,统一电动机工作效率为92%,电池充放电效率为91%,传动系统效率为99%; ④ 单次工况制动终止车速为0 km·h-1.

电动机实现动能和电能之间的转换,理想电动机转矩特性为低于额定转速恒转矩输出,高于额定转速恒功率输出[10].电动机模型依据试验数据采用查表方式建立,制动时利用实时车速查得所能提供最大再生制动力,输入到控制策略模块计算实际可提供电动机制动力,并按控制策略分配制动力.电动机的相关参数:电动机峰值(额定)转矩为382(191)N·m;电动机峰值(额定)功率为60(30)kW;电动机峰值(额定)转速为4 500(1 500)r·min-1.忽略电池温度对电池性能的影响,采用电池Rint模型,电池荷电状态(state of charge,SOC)采用安时累积法计算[11].电池参数:额定电压为320 V;额定容量为120 A·h;最大充电(放电)电流为100(180)A;SOC初值为0.8.

3 最优制动强度理论与仿真分析

3.1 理想再生制动控制策略

再生制动系统结构可依据电动机和摩擦制动系统起作用的方式分为串联和并联2类,研究的车型采用串联结构,电动机和摩擦制动力可以单独调整控制.针对不同情况,传统再生制动分配策略主要包括理想制动力分配策略、并行制动力分配策略和最佳能量回收分配策略等[12].

采用的理想再生制动控制策略选用文献[12]设计的理想再生制动力分配策略,分配前后轴制动力、前轴电动机制动力和摩擦制动力.为保证低速制动稳定性和电池充电安全性,当制动强度z>0.8,SOC>0.95或车速低于10 km·h-1时,前轴电动机制动力退出,制动力完全由摩擦制动力承担.

3.2 最优制动强度理论分析

电动汽车制动和加速时轴荷会发生转移.制动时,前后轴载荷转移程度受制动强度影响,考虑到理想再生制动力分配策略依据前后轴载荷比例分配制动力,因此载荷变化时前后轴制动力分配也不同.对于集中电动机前轴驱动电动车而言,只有前轴有能量回收的能力,并受前轴电动机峰值功率限制.

当前轴分配的制动力高于电动机可提供制动力时,前轴必然需要摩擦制动力参与,能量回收不是最优状态;当制动强度较小时,制动距离将延长,通过滚动阻力和空气阻力消耗的功率增加,而此时分配给前轴的制动力有可能小于电动机可提供制动力,没有充分发挥电动机的再生制动能力.综上可知,制动时若分配给前轴的制动力刚好与电动机当前可提供的制动力相等,前轴摩擦制动力不参与,从而使制动能量回收效果最优.

因此从前轴电动机峰值制动力考虑,计算出当前状态下前轴无摩擦制动参与的整车制动强度,即为当前工况下可使能量回收最优的制动强度.前轴分配的制动力与电动汽车的结构参数、阻力和制动强度有关,理想状态下,当前轴制动力完全由电动机提供时,忽略旋转部分的影响,汽车纵向动力学方程如下:

mgz-Fw-Ff=Fm+Fzrz,

(1)

式中:m为整车整备质量;g为重力加速度;Fw,Ff分别为空气阻力和滚动阻力;Fm为电动机制动力;Fzr为后轴垂直载荷.

(2)

式中:a为质心到前轴的距离;hg为质心高度;L为轴距.

(3)

式中:Tm为电动机输出转矩;ig,i0分别为变速器传动比和主传动比,研究的车型有主减速器无变速器,i0=4.1,ig=1;R为车轮滚动半径;ηt为传动系统效率.

Ff=mgf,

(4)

式中f为滚动阻力系数.

(5)

式中:A为迎风面积;CD为空气的阻力系数;v为车速.

由式(1)-(5)得到理论最优制动强度:

(6)

考虑到低速制动稳定性、日常行车速度和本车最高车速(130.0 km·h-1)的影响,将制动初始车速研究范围设定为10.0～120.0 km·h-1.在车速范围内,理论最优制动强度变化曲线如图3所示.

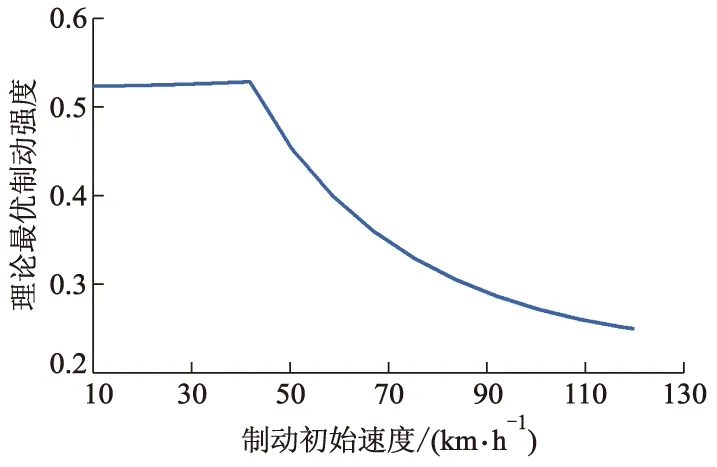
图3 理论最优制动强度分布曲线

从图3可以看出:理论最优制动强度变化曲线与电动机转矩特性曲线变化趋势相近,说明电动机工作特性是影响zoptt的主要因素.当车速为10.0～41.9 km·h-1(对应低于电动机额定转速范围)时,电动机输出峰值转矩可提供的制动力较大,因而zoptt较大,zoptt最大值为0.53;高于额定转速时,随着车速增大,电动机输出转矩降低,zoptt逐渐减小,车速为120.0 km·h-1时,zoptt最小为0.25.

理论分析过程建立在理想状态下,只考虑了电动机工作特性、理想制动力分配和阻力对最优制动强度分布的影响.考虑到能量回收效果还与制动持续时间有关,而制动持续时间受z影响.制动持续时间不同时,制动距离、阻力消耗能量、回收能量、电池损耗等不同,这些因素都是理论分析所不能考虑全面的.针对这一情况,将采用仿真分析法研究实际运行过程中最优制动强度分布规律.

3.3 最优制动强度仿真分析

采用制动能量回收率(αr)作为能量回收情况评价指标,定义为制动回收能量与总制动能量之比.

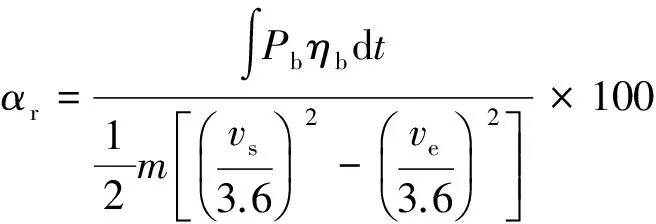
(7)

式中:vs和ve分别为制动初始和终止速度;Pb为电池充电功率;ηb为电池充电效率.

采用制动阻力消耗率(αc)作为阻力消耗能量情况评价指标,定义为阻力消耗能量与总制动能量之比.

(8)

3.3.1 正交试验设计

根据数理统计中格列汶科定理,可以利用样本去推断总体,另外考虑到制动工况中单一因素对制动能量回收的影响存在一定规律[7-8],采用正交试验设计(orthogonal test design,OED)安排仿真试验.OED具有采样均匀分散整齐可比的特点,借助于构造的正交分析表,在保持各因素水平搭配均衡的前提下进行组合试验,在试验次数较少条件下找到最优因素水平组合.针对研究对象的特点,以能量回收率最优为目标,z和vs为试验因素,选取具有代表性的试验水平,设计正交试验,寻找能量回收率最高因素和水平组合.车速为10.0～120.0 km·h-1时,50个水平均匀分布;考虑到常用制动强度范围[13],z在0.22～0.80范围内以等距0.02进行分布,z在0.01～0.22范围内以等距0.01分布,共51个水平,试验次数为2 550次.正交试验结果如表1所示.

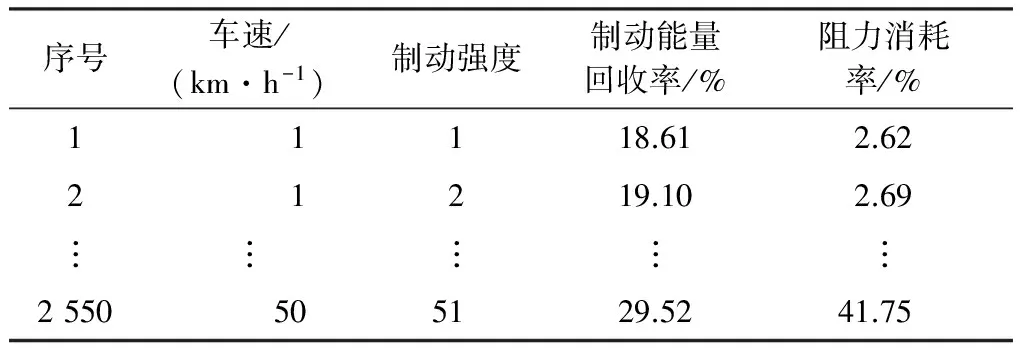
表1 正交试验结果

3.3.2 仿真结果分析

采用前文的理想再生制动控制策略,研究实现能量回收最佳的最优制动强度分布规律,典型车速采样点下制动能量回收率和制动阻力消耗率随制动强度的变化曲线分别如图4,5所示,仿真最优制动强度(zopts)随车速变化曲线如图6所示,zopts下能量回收率与阻力消耗率曲线如图7所示.

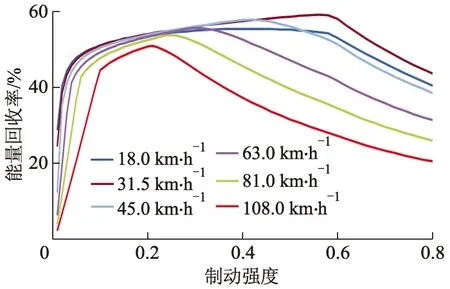
图4 典型车速制动能量回收率

图5 典型车速制动阻力消耗率

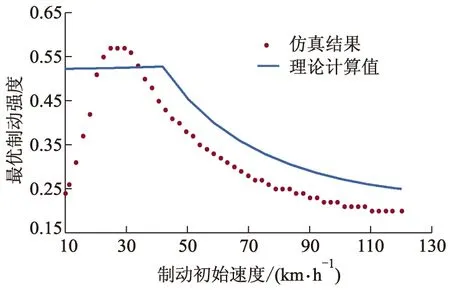
图6 最优制动强度分布曲线

图7 最优制动强度能量回收率和阻力消耗率

从图4,5可以看出:单次工况中vs不变时,z对αr影响较大,随着z的减小,αr先增加再减小,存在使αr最大的制动强度;z较小时,αr迅速下降,αc迅速增大.分析认为,z较小时制动持续距离长,造成阻力消耗和损耗增多;当z过小时,汽车需求制动力完全由阻力提供,电动机制动力不再参与,无能量回收.

从图6可以看出:vs不同时zopts不同,zopts与zoptt变化趋势相近,但两者存在差异.zopts变化趋势:随着vs增加,zopts先增加到峰值0.57,然后随着vs继续增加,zopts逐渐减小,在某一车速(110.3 km·h-1)后再稳定于zopts=0.20;在中高车速下zopts与zoptt变化趋势一致,但两者不完全相同,在低速阶段,zopts与zoptt差别较大.分析认为,zopts和zoptt都考虑了理想再生制动力分配策略、电动机转矩特性和空气阻力、滚动阻力的影响,所以两者有着相似的变化趋势;从图4,5和7可以看出:制动能量回收效果与阻力消耗大致成反比变化,而阻力消耗与制动持续时间成正比变化,zoptt分析时并未考虑到制动持续时间、电池工作特性等因素的影响,这正是理论与仿真结果存在差异的原因.

从图7可以看出:随着车速的增大,αr先增大(峰值点为vs=31.5 km·h-1,αr=56.04%)后减小,αc变化(最小值出现在vs=24.8 km·h-1,αc=0.86%)与之相反,两者峰值是vs和zopts交互作用的结果.另外高速时αc较高,这主要是因为速度越高空气阻力越大造成的.

综上所述,采用最优制动强度制动时,整车需求制动力、前轴分配制动力、电动机制动力、摩擦制动力和阻力可以协调到实现能量回收率最高的最佳匹配点.vs高于电动机额定转速对应速度时,电动机可提供制动力矩随vs增大而减小,行驶阻力随vs增大而增大,此时最优制动强度较小,可以减少前轴分配制动力,满足电动机制动力矩较小这一条件,降低摩擦制动力消耗,但制动强度不能过小,否则延长制动持续时间或制动力完全由阻力提供时,阻力消耗能量增多;vs低于电动机额定转速对应车速时,电动机恒转矩输出,且行驶阻力较小,此时最优制动强度较大,可以使前轴分配制动力增大,充分发挥电动机转矩较高的优势;另外vs较小时,行驶阻力很小,可以适当减小制动强度(虽说制动强度减小使得电动机峰值制动转矩得不到充分利用,前轴部分制动力由摩擦制动提供,但延长制动持续时间可以使回收能量增多),但制动强度不能过小,否则阻力消耗能量将远大于制动回收能量.

4 再生制动能量回收最优控制策略

4.1 最优控制策略设计

从理论和仿真分析结果得出,仿真最优制动强度zopts考虑能量回收影响因素更多,在理论分析时这些因素往往被忽略.另外图4表明,最优制动强度附近,在一定范围内,也有较好的能量回收效果,这为应用仿真结果带来了便捷性,只要保证制动强度在合适的范围内,就可以保证能量回收效果整体较优.

为反映最优制动强度变化规律,采用最小二乘法对仿真数据进行多项式拟合.依据数据点分布特点和拟合经验,在满足拟合精度的约束下,选用10次多项式拟合最优制动强度数据,获得最优制动强度拟合方程:

(9)

式中:zopt为拟合最优制动强度;ai为拟合系数.

最优制动强度拟合数据曲线如图8所示,仿真点在拟合曲线附近分布比较均匀,偏离程度较小,说明拟合曲线能较好地反映仿真最优制动强度的变化趋势.

图8 最优制动强度拟合曲线

结合前文理想再生制动控制策略和最优制动强度的分析，制定再生制动能量回收最优控制策略，在不同制动初始速度下提高能量回收效果.最优控制策略主要包含2部分：制动力分配(前后轴制动力分配、电动机和摩擦制动力分配)和最优制动强度控制.制动力分配、驱动和制动模式判别采用前文提到的理想再生制动控制策略，最优制动强度根据式(9)计算得到，与vs有关.

单次工况下,首先判断制动模式和再生制动工作条件,依据vs获得zopt作为目标制动强度,按照理想制动力分配策略分配各车轮的制动力.再生制动能量回收最优控制策略控制流程如图9所示.图中:as为初始制动减速度(踩下踏板瞬间),用于判断制动、驱动模式;v为车速；zp为初始制动强度;FbfI和FbrI分别为按照I曲线分配的前轴和后轴制动力;Ffm和Fff分别为前轴实际电动机和摩擦制动力;Ffr为后轴制动力.

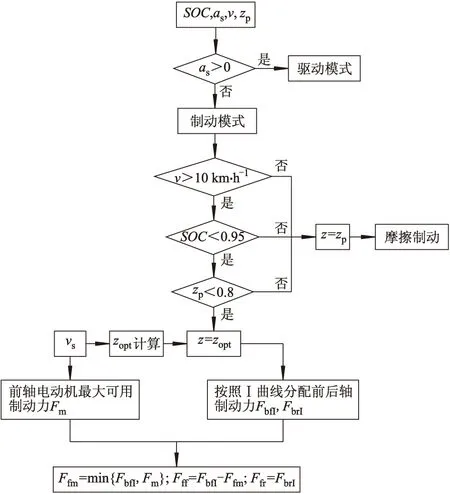
图9 再生制动能量回收最优控制策略

4.2 最优控制策略验证

选取3个试验制动初始速度(不包含在正交表内):30.0,50.0,80.0 km·h-1,验证制动能量回收最优控制策略的效果,并与理想再生制动控制策略对比,仿真结果如表2所示.

表2 仿真结果

从表2可以看出:再生制动能量回收最优控制策略的能量回收率均比理想再生制动控制策略高,制动能量回收最优控制策略可以依据制动初始速度计算最优制动强度,并按照此强度制动,达到了提高制动能量回收率的目的.最优控制策略工作时,可能导致制动距离和持续时间较长,可应用于对制动距离和持续时间要求较低的场合.

5 结 论

1) 制动单次工况中,通过分析制动强度与制动能量回收效果之间的关系,获得能量回收效果最佳的最优制动强度,使用最小二乘法获得最优制动强度拟合方程,并结合理想再生制动控制策略,设计再生制动能量回收最优控制策略,以提高单次工况下能量回收效果.与理想再生制动控制策略进行仿真对比表明最优控制策略可以实现能量回收效果最优.

2) 采用理论和仿真分析的方法,研究能量回收与制动强度之间的关系,结果表明:制动强度对能量回收效果影响较大,单次工况下,最优制动强度之所以能实现能量回收效果最优,是因为在此制动强度下制动时整车制动力需求、前轴分配制动力、电动机制动力、摩擦制动力和行驶阻力可达到最佳匹配,这一匹配关系可以通过能量回收率和阻力消耗率体现出来.

)

[1] 赵轩, 马建, 汪贵平. 基于制动驾驶意图辨识的纯电动客车复合制动控制策略[J]. 交通运输工程学报, 2014, 14(4): 64-75.

ZHAO X, MA J, WANG G P. Composite braking control strategy of pure electric bus based on brake driving intention recognition[J]. Journal of Traffic & Transportation Engineering, 2014,14(4): 64-75. (in Chinese)

[2] XU L F, OUYANG M G, LI J Q, et al. Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost[J]. Applied Energy, 2013, 103(1): 477-487.

[3] 董昊轩, 郭金刚, 闫宽宽. 轮毂电机四轮独立驱动电动汽车再生制动控制策略[J]. 机械科学与技术, 2017, 36(11): 1778-1784.

DONG H X, GUO J G, YAN K K. Control strategy of regenerative braking for four-wheel-drive electric vehicles of in-wheel-motor[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(11): 1778-1784. (in Chinese)

[4] KUMAR C N, SUBRAMANIAN S C. Cooperative control of regenerative braking and friction braking for a hybrid electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers Part D:Journal of Automobile Engineering, 2015, 230(1): 103-116.

[5] CAO X H, ISHIKAWA T. Optimum design of a rege-nerative braking system for electric vehicles based on fuzzy control strategy[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2016, 11(S1): S186-S187.

[6] SUN F C, LIU W, HE H W,et al. An integrated control strategy for the composite braking system of an electric vehicle with independently driven axles[J]. Vehicle System Dynamics, 2016, 54(8): 1031-1052.

[7] 王猛, 孙泽昌, 卓桂荣, 等. 电动汽车制动能量回收最大化影响因素分析[J].同济大学学报(自然科学版),2012, 40(4): 583-588.

WANG M, SUN Z C, ZHUO G R, et al. Maximum braking energy recovery of electric vehicles and its influencing factors[J]. Journal of Tongji University(Natural Science), 2012, 40(4): 583-588. (in Chinese)

[8] 张树培, 黄璇, 张玮. 电动汽车道路行驶制动能量回收特性研究[J]. 汽车技术, 2014(12): 49-53.

ZHANG S P, HUANG X, ZHANG W. Research on braking energy recovery characteristics of electric vehicle in road driving[J]. Automobile Technology, 2014(12): 49-53. (in Chinese)

[9] GUO J G. Development of regenerative braking for electric vehicle in China: a review [J]. International Journal of Electric and Hybrid Vehicle, 2015, 7(2): 120-138.

[10] EHSANI M, GAO Y M, GAY S. Characterization of electric motor drives for traction applications[C]∥An-nual Conference of the IEEE Industrial Electronics Socie-ty. USA:IEEE, 2003: 891-896.

[11] WANG B, LI M, XU M, et al. Simulation-based energy flow study of purely electric-drive vehicles [C]∥Proceedings of the FISITA 2012 World Automotive Congress. Beijing, China: SAE, 2012: 615-630.

[12] GAO Y M, CHEN L P, MEHRDAD E. Investigation of the effectiveness of regenerative braking for EV and HEV[C]∥SAE Technical Paper Series. USA: SAE Publication Group, Paper Number: 1999012901.

[13] CIKANEK S R, BAILEY K E. Regenerative braking system for a hybrid electric vehicle[C]∥Proceedings of the American Control Conference. USA: AACC,2002: 3129-3134.