基于Copula函数的切削力与表面粗糙度的相关性

裴宏杰, 李公安, 付坤鹏, 陈少峰, 王贵成

(江苏大学 机械工程学院, 江苏 镇江 212013)

智能制造是制造业的一个重要发展方向[1].为了实现机械加工的智能化,需要在线监测生产加工过程,因而机械加工表面质量和监测参数之间的相关关系成为了一个重要问题.在机械加工过程中,切削力是常用的监测信号[2],表面粗糙度是衡量表面质量的一个重要指标,因此研究切削力和表面粗糙度之间的相关性,对实现切削加工自动化生产具有重要的意义.

早期研究[3-4]采用线性相关系数描述分析变量间的相关关系,无法准确度量切削过程变量之间复杂的非线性、非对称关系.进而文献[5-7]运用数理统计的方法,得出切削过程变量之间的相关关系.文献[8]通过采用自适应神经模糊推理系统模型来讨论切削参数和切削力以及表面粗糙度之间的相关程度大小.

作为一种新的相关性研究方法,Copula函数既能构造多变量的联合分布函数,也能很精确地描述它们的相关结构,而且可以定量地描述样本数据的厚尾特性,近些年来被广泛应用于金融、电力、水文和故障诊断等领域[9-10].但是在机械加工领域的应用较少,因而文中基于Copula函数以及由其所构造的联合分布函数对切削力和表面粗糙度变量之间存在的相关关系进行有效分析.

1 试验设置

试验机床采用SB-CNC超精密车铣复合中心,刀片型号CCGX 09 T308-AL H10,圆角半径RE为0.8 mm,前角γo为0°,后角αo为7°,主偏角Kr为95°,副偏角Kr′为5°.工件材料选用直径Φ30 mm的7075高强度航空铝合金,表面粗糙度和切削力分别通过Olympus公司DSX500光学数码显微镜和Kistler公司9293A压电式测力仪得到.试验方法采用控制变量法,冷却方式为干切削,试验总数为64组,结果如表1所示.

表1 车削试验结果

注:v为切削速度;f为进给速度;ap为切削深度;Fx为轴向力；Fy为径向力;Fz为切向力;Ra为表面粗糙度

2 Copula函数

Copula函数是一个连接多维联合分布和边缘分布的函数,根据Sklar定理[11]表述:X,Y变量的联合分布函数为H(x,y),其边缘分布函数分别是u=F(x),v=G(y),则必定存在一个Copula函数C(u,v),对任意的x,y∈R均满足下式:

H(x,y)=C(u,v)=C(F(x),G(y)),

(1)

式中:H(x,y)是边缘分布F(x),G(y)的联合分布函数;C就是连接函数Copula函数.

2.1 Copula函数的参数估计

由于切削力与表面粗糙度变量都服从正态分布,所以首先将各变量样本值转换为[0,1]区间内的概率分布值(用U,V表示),再利用MATLAB中的相关命令计算得到Copula函数中所包含的未知参数估计值,其结果如表2所示.

表2 切削力与表面粗糙度变量的建模参数

2.2 Copula函数的确定

将选用L2距离最小法来对5种待选的Copula函数进行最优选择.将经概率积分变换后的样本值代入到各个待选Copula函数以及样本的经验分布函数中,就可以获得样本数据对应的理论概率值和经验概率值,然后通过计算两者的欧式距离,并以此作为函数选择的评价标准,其计算结果如表3所示.

表3 切削力与Ra变量对应的欧式距离d2

从表3可知,根据拟合优化选择的标准,Frank Copula函数对应的欧式距离d2最小,因此将选用Frank Copula函数来描述Fx,Fy,Fz以及F各变量与Ra变量的相关结构.

2.3 联合分布函数模型的建立

根据Sklar定理,轴向力Fx、径向力Fy、主切削力Fz以及切削合力F各变量与表面粗糙度Ra变量的联合分布函数分别如下式所示:

(2)

(3)

(4)

(5)

式中的建模参数α分别是3.287 5,4.250 5,4.018 6和4.118 5.

为了验证各切削力变量与表面粗糙度变量所建立的联合分布函数模型的合理性,可以通过比较各个观测样本数据(xi,yi)所对应的经验累积概率值与理论累积概率值是否近似相同来判断.根据式(2)-(5)可以计算出各切削力变量与表面粗糙度变量样本点所对应的理论累积概率值;而计算经验累积概率值的方法可以参照文献[12],公式如下:

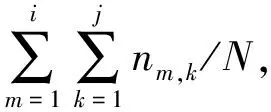
(6)

式中N表示随机变量的样本总数；nm,k指的是样本值(xm,yk)出现的频数.根据经验累积概率与理论累积概率计算结果,将切削力与表面粗糙度两相关变量各个观测样本数据(xi,yi)的理论累计概率Fthe值作为纵坐标,经验累计概率Femp值作为横坐标,分别画出各变量对应的散点图,其结果如图1-4所示.

从图1到图4中可以看出,各相关变量所对应的理论值与经验值基本在一条直线上,并且两者的线性相关系数r分别是0.994,0.995,0.991和0.992,说明切削力变量与表面粗糙度变量的联合分布函数模型与实际情况拟合效果好.

图1 Fx与Ra观测数据经验累积概率与理论累积概率散点图

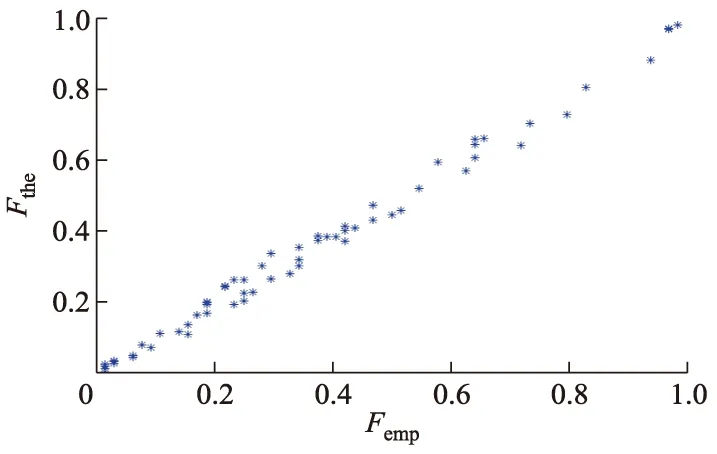
图2 Fy与Ra观测数据经验累积概率与理论累积概率散点图

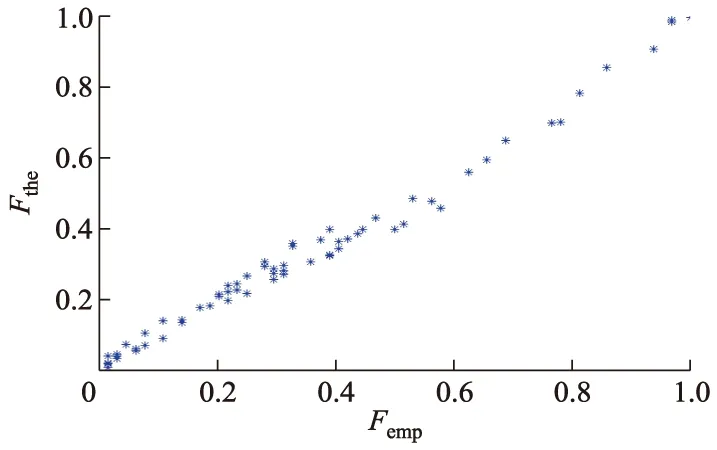
图3 Fz与Ra观测数据经验累积概率与理论累积概率散点图

图4 F与Ra观测数据经验累积概率与理论累积概率散点图

3 切削力与表面粗糙度相关性分析

3.1 整体相关性

为了分析比较各切削力分量与表面粗糙度的整体相关性,选用由Copula函数导出的Kendall秩相关系数τ作为评价指标;同时,由于它们的相关结构形式可以由Frank Copula函数来表达,依据文献[10,12]可以计算得到Fx与Ra,Fy与Ra,Fz与Ra,F与Ra的τ值分别为0.331 8,0.404 6,0.389 5和0.396 9,检验水平α=0.01上显著相关(双尾).

所有方向的切削力与表面粗糙度之间都存在着显著的相关性,并且径向力与表面粗糙度之间的关联程度最强,主切削力次之,轴向力对表面粗糙度的影响最弱;同时,切削合力与表面粗糙度也有着极强的相关性.由此可知,切削力与表面粗糙度的关联性程度较大,整体上有一定的协同性.此外,由于径向切削力垂直于加工表面,因此,径向力的变化与工件表面轮廓高度的波动有着密切的联系,于是它们之间的相关程度也最强.

综上所述,切削力与表面粗糙度整体上有着明显的正相关性,并且各切削力分量与表面粗糙度之间的相关程度大小并不一致.

3.2 尾部相关性

在切削过程中,由于工件的不均匀性以及刀具磨损程度的变化,切削力可能会出现极大或者是极小的情况,为了有效地控制表面质量,极值条件下的切削力与表面粗糙度相关性分析也是不可或缺的.通过切削力与表现粗糙度的尾部相关性分析,可以定量地揭示它们在极值条件下的相关关系.上下尾部相关系数和Copula函数之间的关系如下:

(7)

(8)

式中:λu和λl表示上、下尾相关系数;q代表分位数.根据式(7)和(8)可以计算得到各切削力分量及切削合力与表面粗糙度在不同概率q条件下对应的上尾及下尾相关系数,分析结果如表4所示.

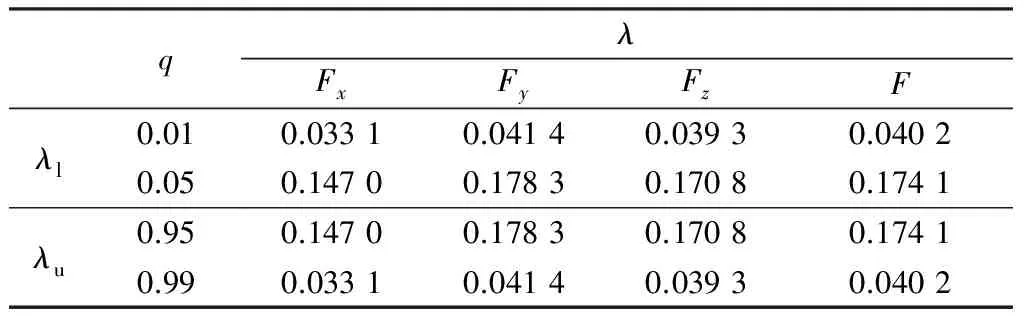
表4 切削力与表面粗糙度Ra的尾部相关系数

由此可知,各切削力变量与表面粗糙度变量的上、下尾相关系数相等,并且在同一水平q的条件下,径向力Fy对应的尾部相关系数最大.同时,随着水平值q的增大,各变量对应的上尾相关系数趋向于0,而随着水平值q的减小,其下尾相关系数也近似为0,这说明了极值条件下的切削力对表面粗糙度的影响程度较小,即关联性不强.

4 结 论

1) 切削力与表面粗糙度之间存在着明显的正相关关系,并且各切削力分量所对应的相关程度大小并不一致,径向力、主切削力以及轴向力依次对应的Kendall秩相关系数依次减小,说明径向力对表面质量的影响程度最大,轴向力影响最小;同时,切削合力能够较好地表征各分量的综合作用.

2) Frank Copula函数能够较好地刻画切削力与表面粗糙度两变量的相关结构,并且其结构是关于中心对称的.

3) 切削力与表面粗糙度的上、下尾相关系数相等,并且它们之间的尾部相关程度较小.

)

[1] 《国务院关于印发“中国制造2025”》的通知[R].中华人民共和国国务院公报,2015.

[2] LAURO C H, BRANDAO L C, BALDO D,et al. Monitoring and processing signal applied in machining processes: a review[J]. Measurement, 2014,58(58): 73-86.

[3] 特伦特. 金属切削理论[M]. 北京：机械工业出版社,1980.

[4] JUNEJA B L, SEKHON G S. Fundamentals of Metal Cutting and Machine Tools[M]. New Delhi: Wiley Eas-tern, 1987.

[5] HUANG B, CHEN J C. An in-process neural network-based surface roughness prediction (INN-SRP) system using a dynamometer in end milling operations [J]. The International Journal of Advanced Manufacturing Technology, 2003, 21(5): 339-347.

[6] CUS F, ZUPERL U. Surface roughness control simulation of turning process[J]. Journal of Mechanical Engineering, 2015,61(4): 245-253.

[7] 王明微,周竞涛,敬石开,等.基于贝叶斯网络的切削加工表面粗糙度在线监测方法[J].计算机集成制造系统,2014,20(12): 3075-3081.

WANG M W, ZHOU J T, JING S K, et al. Surface roughness monitoring method based on Bayesian network models.[J].Computer Integrated Manufacturing Systems, 2014, 20(12): 3075-3081. (in Chinese)

[8] MAHER I, ELTAIB M E H. Cutting force-based adaptive neuro-fuzzy approach for accurate surface roughness prediction in end milling operation for intelligent machining[J]. The International Journal of Advanced Manufacturing Technology,2015,76(5): 1-9.

[9] 吴雨薇.区域多风场接入电网的相关问题研究[D].南京:东南大学,2015.

[10] 何庆升,朱永忠. 应用高维Copula函数的月径流量联合概率分布研究[J].重庆理工大学学报(自然科学), 2013,27(8):112-120.

HE Q S,ZHU Y Z. Research on joint probability distribution of monthly runoff using high dimensional Copula function[J]. Journal of Chongqing University of Technology(Natural Science), 2013,27(8):112-120. (in Chinese)

[11] SKLAR A. Fonctions de repartition an dimensions et leurs marge[J]. Publ Inst Statist Univ Paris, 1959, 8: 229-231.

[12] 李寿贵, 余胜春. 概率论与数理统计[M]. 北京: 科学出版社,2016.