一种改进的二维Otsu图像分割算法研究*

鲁秋菊

(陕西理工大学 数学与计算机科学学院，陕西 汉中 723000)

在计算机视觉系统中，对图像进行分割是一项重要的步骤，它将锁定的目标从背景中取出，为识别、分类、检索等提供支持[1].图像信息是人类收集外部世界信息的主要途径，因而计算机的视觉系统非常重要.在一个图像中，往往人们所需要的只是图像中某个区域的一部分，所以就需要利用图像中的纹理、轮廓等图像特性来进行提取，以分析目标[2].本文在图像特性的提取中使用了Otsu算法以完成对图像的分割.

Gong在二维Otsu算法的基础上提出了快速递推算法[3]；汪海洋对算法进行了改进[4]，使用迭代的方式来构建索引表，减少了二维Otsu算法的计算量，使得复杂度由O(L4)降到O(L2)；陈修桥对快速递推算法进行了改进，加快了二维最大准则的计算速度；吴成茂[5]对二维的最大熵进行了改进，并且在假设二维直方图的联合概率密度是连续的情况下提出了他的快速迭代的算法.在提高分割算法的速度和效率的方向上，有学者发现使用群智能算法是一个非常有效的方式[6].为了提高算法的性能，Tao[7]引入了蚁群优化模糊墒算法；Xu[7]证明了阈值分割出的背景与目标的均值平均值为Otsu法的最佳阈值.潘喆[8]在最佳阈值的查找中使用了人工鱼群智能算法，与传统的算法相比，大大提高了算法的速度，以更少的迭代次数、更少的种群来达到算法的收敛.Sathya[9]在进行多阈值分割时，使用了细菌觅食算法.智能算法与传统的穷举法相比，虽然在效率上较好，但是其不稳定性致使在实际使用中存在着一定的劣势.

本文在分析了相关算法的基础上，使用二维Otsu算法来进行研究，以获取目标与背景图像分割较好的性能，并引入遗传算法，对算法进行改进，降低算法复杂度，提升算法的运行效率.

1 二维Otsu算法

在传统的一维Otsu算法中，由于只对像素点的灰度信息进行了考虑，没有将周围像素点的影响纳入考量的范围，所以在进行图像的分割时，往往会出现较大的误差.在一维Otsu算法的基础上，提出二维的Otsu算法，以原图以及周边的像素平滑信息来建立二维直方图，减小了在进行图像分割时的误差，提高了算法的准确度.

二维Otsu算法中使用的最大类间方法本质是阈值化分割方法，该种方法的核心内容如下：将图像设为f(x,y),(1≤x≤M,1≤y≤N),图像的灰度为L，大小为M×N，而邻域平滑图像g(x,y)就可以使用像素点n×n的邻域的平均灰度值来获取到，g的灰度也是L.如此一来，在图像的每一个像素中，都可以构成一个二元组，即像素以及图像相邻域二者的灰度值.使用fij代表在图像f中的灰度值i且邻域灰度值j的像素点在同一个空间位置上的个数，使用所得到的数据就能构建出在该点的二维直方图.图像的灰度等级为：

式中，k代表的是在像素点中正方形邻域的宽度，一般为奇数.如图1所示为图像在二维直方图中的平面投影图.

灰度分割的阈值为s,邻域的灰度值为t，使用(s,t)将图像分成两个类别，即背景和目标.并且满足0≤s≤L-1,0≤t≤L-1，此时就可以对背景和目标所占图像的比例进行计算.

2 改进的二维Otsu图像分割算法

由于一维没有利用图像的局部空间信息，当存在噪声干扰或灰度分布交叉时，图像分割效果不佳，为此有学者提出了二维Otsu阈值分割方法，对像素点自身以及邻域灰度值的情况进行了充分考虑，提升了算法的抗噪能力[11]，但算法在实际使用中，计算复杂，实时性不强.有的学者对类内的离散测度进行了考量，促进了类的完整性，但是提高了算法的复杂度，性能的消耗增加.本文将对这两个弊端进行改进，借以提出新的算法.

2.1 类内的离散度

阈值的选取是利用阈值法进行图像分割的关键所在，如果阈值选择的值过小，那么背景部分就有可能成为目标点，如果阈值过高，那么目标点就有可能成为背景点.阈值是图像分割精度的关键点，若不够准准确就会造成图像分割的误差，进而丢掉有用的信息，所以图像分割中阈值的选择十分重要.

在传统的Otsu算法中进行阈值分割时，对前景及背景的方差进行了考虑，并且分割效果也较好，但是没有将类内自身的离散性纳入考量的范围，所以，分类的好坏无法得到充分的体现.为了改善这种情况，本文引入了类内离散度，以使得分割时达到类间方差最大，实现类内的一致性.

像素灰度值所对应的分类离散测度表示为：

τdi=ωodoi+ωbdbi，

τdj=ωodoj+ωbdbj，

2.2 改进的Otsu算法

为了改进二维Otsu算法在复杂度上的问题，本文对Otsu算法进行改进，将二维算法拆成两个一维的Otsu算法.利用灰度值的一维直方图来得到阈值，以帮助我们提取目标；利用邻域平均灰度值的直方图获取到用于消除噪声的阈值.这两个得到的阈值就可以替代原本二维Otsu算法中的两个阈值.该方法与一维Otsu算法相比，它将图像的灰度信息以及像素点相邻区域的灰度信息都纳入了考量的范畴，因而具有了更加优秀的降噪能力.另一方面，因为使用了两个一维的Otsu算法，因此降低了算法的复杂度，下文就此进行详细的说明.

这两类的总均值矢量:

由此推出像素灰度值i所对应的一维类间方差如下：

σBi(s)=ωo(μoi-μi)2+ωb(μbi-μi)2.

(1)

相邻区域灰度值j对应的一维类间方差为：

σBj(t)=ωo(μoj-μj)2+ωb(μbj-μj)2.

(2)

而

并且

这两类的平均矢量为：

总均值矢量为：

依据一维Otsu算法的原理，两个类别最佳的阈值s*,t*应满足如下条件：

2.3 改进的阈值选取算法

利用上面所述的公式构建出新的阈值识别函数：

ψj=ωo(1-ωo)×σBi/τdi，ψj=ωo(1-ωo)×σBj/τdj.

(3)

为了使离散度最小，获取最好的分割效果，我们需要应用式(3)求取ψi、ψj最大值，即τdi,τdj的最小值，以保证在类间有较好的分离性，同时也使得在同一类内有着较好的一致性.在图像的灰度复杂度为L时，本文的算法即上述的两个一维的Otsu算法的复杂度为O(L+L)=O(L),远远小于二维Otsu算法的复杂度O(L4)，大大提升了算法的性能.

本文使用遗传算法来求取合适的阈值向量(s,t)，以用来快速实现图像的分割阈值的确定.有了分割阈值就能对灰度图像进行二维阈值化分割.

2.4 基于遗传算法的阈值优化

(1) 初始化.利用随机数生成一个随机的行数size、16列的矩阵来作为初始的种群.

(2) 编码.二维Otsu算法所待分割的阈值是二维的，所以使用16位二进制码来对二维分割阈值，前8位代表的是分割阈值s后8位代表的是分割阈值t，x=(x0,…，x7,x8,…，x15).

(3) 适应度函数.利用式(1)及式(2)，取出最大值时对应的参数s、t，即为我们所需要的分割阈值.

(4) 选择.使用适应度比例法进行选择，适应度越高的，被选择的概率就越高.

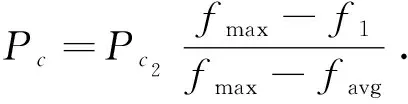
算法的终止条件为:当算法的迭代次数达到的预先设定的值或者当前群体的平均适应度与上一代的平均值之差小于1×10-4时，终止算法.

3 仿真实验与结果分析

为了检验本文所提算法的图像分割效果与计算速度上的优越性，选择有噪声图像为实验对象，分别选取目前经典的二维Otsu图像分割相关的改进算法：灰度-平均度法、平均灰度-梯度法[10]与本文所提算法进行实验比对，同经典的算法进行图像分割比较，更能说明本文提出的改进二维Otsu图像分割算法其算法性能、分割效果的提升.仿真实验所使用的运行系统为Windows XP，内存为2.0 GB，频率为3.19 GHz，仿真环境为Matlab7.0.

在运行结果对比中，探寻发现在噪声的影响下，使用灰度-平均度法的效果较差，无法识别目标与背景，不能有效完成图像的切割.使用平均灰度-梯度法时，存在较多的噪声点，对噪声的干扰没有较好的抵抗力.使用本文提出的算法时，能够有效地减少噪声的干扰，同时对图片细节的分割能力也较好.具体图像分割效果比对如图2所示.

一般来说，在对图像的分割效果进行判定时，既需要人的主观视觉来进行评判，也需要对应的客观参数.我们使用了房子、月亮、公交车、客机、苹果5张图像作为实验对象，通过图像处理后在区域中表现的一致性和相关属性的对比度来进行客观的各个算法的评定对比.在表1、表2中，我们可以看到几种分割方法的相关评价的数据.所表示的区域一致性的UM的值与区域一致性呈现正相关的关系，一致性UM值越大，对比度GC值越大，则差异越大，此时分割的结果就会越好.在受到了较大的噪声干扰时，使用不同的方法来对同一图像进行处理，在结果的对比上，可以看到通过本文算法所得到的处理结果最好.这是因为我们提出了利用局部方差来进行中心像素点和相邻域像素点的灰度级离散度，而且对像素点的灰度差异进行了有效的反应，也大大减小了噪声的干扰，提高了图像的分割效果.

表1 三种分割算法的区域一致性比较

分割方法月亮公交车客机苹果灰度-平均灰度0.707 70.832 20.934 40.851 1平均灰度-梯度0.798 90.912 30.611 10.923 1本文算法0.911 10.879 30.897 40.938 5

表2 三种分割算法的区域对比度比较

4 总结

优化了二维Otsu阈值分割算法，减少了算法的复杂度.为了更简便算出二维Otsu算法中所需要的阈值，算法使用了两个一维算法来求出所需要的阈值，且在阈值的最优解上，使用了最小类内离散度的概念，加之遗传算法，来避免传统的二维算法需要在整个图像内进行搜索的烦琐过程，将算法的性能大大提升.与其他的文献中的算法比较结果来看，本文算法的时间要远小于其算法，且图像分割的效果也符合实际的需要.